A Detailed Overview of BERT Model Compression Methods

Author | Chilia

Columbia University NLP Search Recommendation

Compiled by | NewBeeNLP

The trend of pre-trained models based on Transformer is to become larger and larger. Although these models show significant improvements in performance, the huge number of parameters also poses challenges for deploying these models.

For BERT model compression, it can generally be divided into 5 types (the same applies to other model compressions):

• Knowledge Distillation: Distilling the capabilities of the teacher model into the student model, where the student is generally smaller than the teacher. We can distill a large and deep network into a small network, or distill an ensemble network into a smaller network.
• Parameter Sharing: Reducing network parameters by sharing parameters, such as ALBERT sharing Transformer layers;
• Parameter Matrix Approximation: Reducing matrix parameters through low-rank decomposition or other methods, for example, ALBERT performs low-rank decomposition on the embedding table;
• Quantization: For instance, reducing from float32 to float8.
• Model Pruning: Removing components that have a small impact on the results, such as reducing the number of heads and removing less influential layers.

This article mainly introduces knowledge distillation, parameter sharing, and parameter matrix approximation methods.

1. Using Knowledge Distillation for Compression

For basic knowledge of knowledge distillation, see: Model Compression | Classic Interpretation of Knowledge Distillation.

Representative papers:

1.1 DistilBERT, a distilled version of BERT: smaller, faster, cheaper, and lighter

DistilBERT belongs to the logits distillation method within knowledge distillation.

Many previous works distilled a “task-specific model” from BERT, i.e., distilling a model for a specific task (such as sentiment classification). What distinguishes DistilBERT is that it performs distillation during the pre-training phase, resulting in a general model that is then fine-tuned on downstream tasks. DistilBERT has 40% of BERT’s parameters (can run on edge devices) while retaining 97% of the language understanding capability.

1.1.1 Loss Function Design

The pre-training loss function consists of three parts:

• Distillation Loss: Softmax the logits of both Student and Teacher at high temperature, and compute the KL divergence between them;
• Supervised Task Loss: In this pre-training problem, it is the MLM task loss of BERT, noting that the output of the Student model is softmaxed at temperature 1;
• Cosine Embedding Loss: Align the hidden vectors of the Student and Teacher using cosine similarity. (This seems similar to intermediate layer distillation)

1.1.2 Student Model Design

The student model uses only half of BERT’s layers; initializes using the parameters of the teacher model. During training, dynamic masking and large batch sizes are used, and the next sentence objective is not used (similar to Roberta). The training data is the same as that used in the original BERT training, but due to the smaller model, training resources are saved.

Fine-tuning is performed on the GLUE (General Language Understanding Evaluation) dataset, with test results:

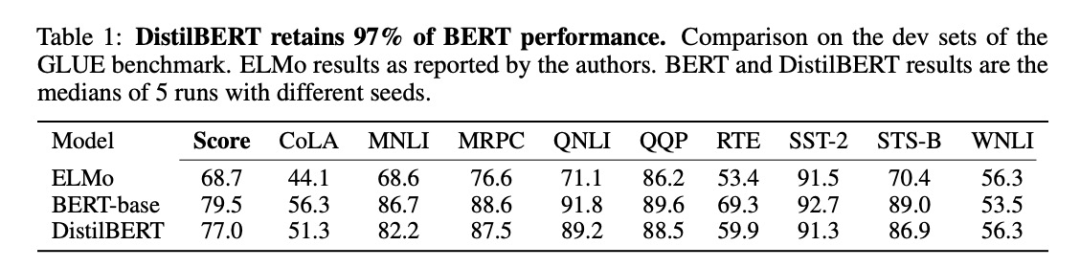
Additionally, the authors researched two-stage distillation (similar to TinyBERT mentioned later), where after pre-training, a BERT model fine-tuned on the SQuAD model is used as the Teacher. During fine-tuning, in addition to the task-specific loss, KL divergence loss with the Teacher’s output logits is also included. I understand this is akin to label smoothing, enabling the Student model to learn more information, thus improving performance:

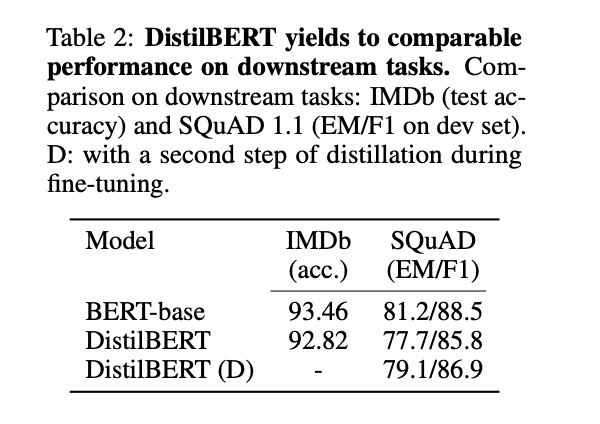DistilBERT(D) represents two-stage distillation, outperforming one-stage distillation + fine-tuning

1.2 TinyBERT: Distilling BERT for Natural Language Understanding

TinyBERT adopts a two-stage learning framework, performing transformer distillation during both pre-training and specific task learning phases. This framework ensures that TinyBERT can acquire both general and task-specific knowledge from teacher BERT.

1.2.1 Transformer Distillation

Assuming the student model has M Transformer layers and the teacher model has N Transformer layers. n=g(m) is the mapping function from student layer to teacher layer, meaning that the m-th layer of the student learns information from the n-th layer of the teacher. Considering the distillation of the embedding layer and the prediction layer, treating the embedding layer as layer 0 and the prediction layer as layer M+1, we have the mappings: 0 = g(0) and N + 1 = g(M + 1). Thus, we have corresponded each layer of the Student with the layers of the Teacher. The paper attempts this mapping for 4 layers and 6 layers, as shown in the figure below (a):

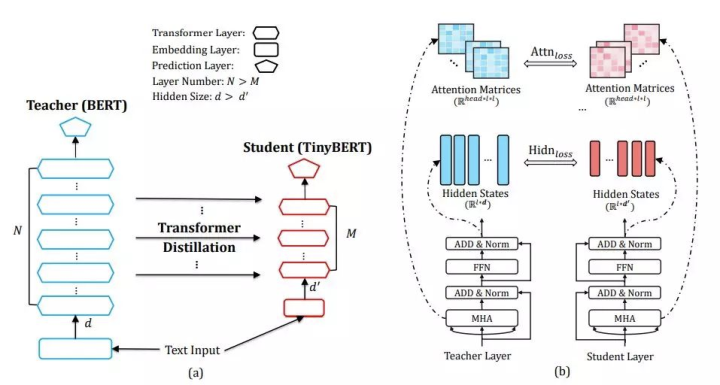
Then, the student’s distillation loss with respect to the teacher is as follows:

For <<student layer m, teacher layer g(m)>, the difference needs to be calculated. How to compute this difference? Below, we look at the four loss functions:

1) Attention Loss

The attention heads of BERT can capture rich linguistic information. Attention-based distillation encourages the transfer of linguistic knowledge from teacher BERT to student TinyBERT. Specifically, the student network learns how to fit the multi-head attention matrix of the teacher network, with the objective function defined as follows:

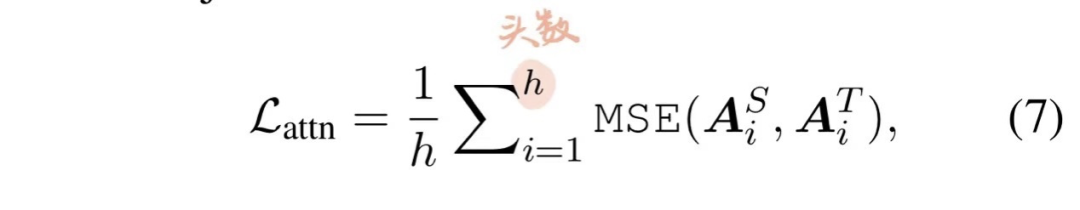
This essentially computes the MSE loss between the i-th attention head of the Student and the i-th attention head of the Teacher; a detail is that the authors only used the original attention matrix A, not the attention matrix after softmax, as this converges better.

2) Hidden Loss

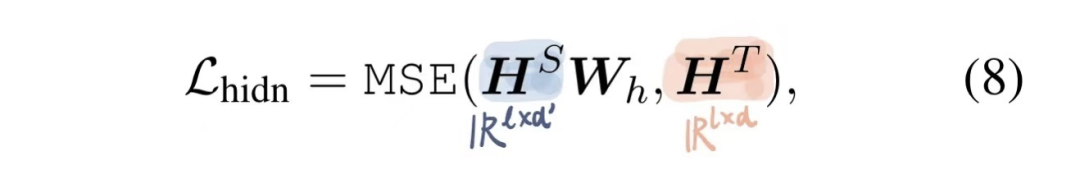
Distilling the output hidden state of each transformer layer. Since the hidden size of the Student is often smaller than that of the Teacher, an adaptation is needed (this is also the idea of intermediate layer distillation). This is also a difference between TinyBERT and DistilBERT — DistilBERT only reduces the number of layers, while TinyBERT also reduces the hidden size.

3) Embedding Layer Loss

Similarly, using adaptation for intermediate layer distillation:

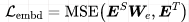
The embedding size is the same as the hidden size.

4) Output Layer Loss

This is logits distillation, calculating the KL divergence of the Student’s output layer with the Teacher’s output layer at temperature t.

The loss function for each layer is categorized into embedding layer, intermediate transformer layer, and output logits layer:

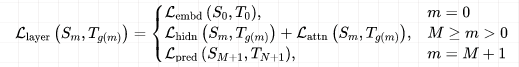
1.2.2 Two-Stage Learning Framework

The application of BERT typically involves two learning stages: pre-training and fine-tuning. The knowledge learned by BERT during the pre-training phase is crucial and needs to be transferred to the compressed model. Therefore, TinyBERT uses a two-stage learning framework, including general distillation and task-specific distillation.

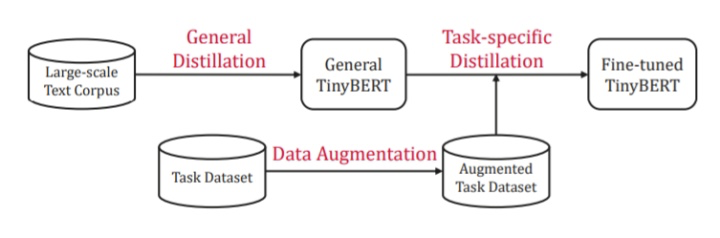
General Distillation

Using pre-trained BERT without fine-tuning as the teacher model, leveraging a large-scale text corpus as learning data, performing the aforementioned Transformer distillation. This results in a general TinyBERT. However, due to the significantly reduced hidden/embedding layer size and number of layers, the general TinyBERT does not perform as well as BERT.

Task-Specific Distillation

Previous research has shown that complex models like BERT have parameter redundancy for specific tasks, meaning similar results can be obtained with smaller models. Therefore, during task-specific distillation, a fine-tuned BERT is used as the teacher model (similar to the method mentioned for DistilBERT, which can be understood as label smoothing). Data augmentation methods are also used to expand the training set for specific tasks.

The data augmentation method mentioned in the article is: for multiple-piece words (those that are split into multiple subwords through word piece), directly find the K closest words in GloVe to replace them; for single-piece words (words that are already subwords), first mask them and let the pre-trained BERT attempt to recover them, taking the K most probable words from BERT’s output for replacement. I understand this is a form of discrete data augmentation, and according to the SimCSE article, this type of data augmentation may introduce some noise ☹️

The two learning stages complement each other: general distillation provides a good initialization for task-specific distillation, while task-specific distillation further enhances the performance of TinyBERT by focusing on learning task-specific knowledge.

2. Parameter Sharing & Matrix Approximation

These two methods are discussed together, taking ALBERT as an example: ALBERT: A Lite BERT for Self-supervised Learning of Language Representations[1]

2.1 Matrix Low-Rank Decomposition (Decomposing the Embedding Table)

ALBERT uses a vocabulary of 30K that is similar in size to BERT. If our embedding size and hidden size are both 768, then if we want to increase the hidden size, we also need to correspondingly increase the embedding size, which will cause the embedding table to become very large.

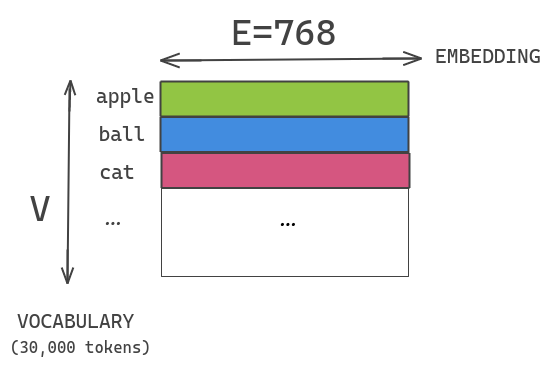
In BERT, … the WordPiece embedding size E is tied with the hidden layer size H, i.e., E = H. This decision appears suboptimal for both modeling and practical reasons. — ALBERT paper

ALBERT resolves this issue by decomposing the large vocabulary embedding matrix into two smaller matrices. This separates the hidden layer size from the size of the vocabulary embedding.

• From a model perspective, since the WordPiece embedding only needs to learn some context-independent representations, while the hidden layer needs to learn context-dependent representations. The strength of BERT-like models lies in their ability to model context-dependent representations. Thus, it should be the case that H >> E.
• From a practical perspective, this allows us to increase the hidden size without significantly increasing the size of the vocabulary embedding parameters.

We project the one-hot encoding vector into a low-dimensional embedding space of E=100, and then project this embedding space into the hidden layer space H=768. This can also be understood as: using an embedding table of E = 100 to obtain the embedding for each token and then transforming it into 768 dimensions through a fully connected layer. This way, the model parameters are reduced from the original to the current .

2.2 Parameter Sharing

ALBERT uses the concept of cross-layer parameter sharing. To illustrate this, let’s look at an example of a 12-layer BERT-base model. We only learn the parameters of the first block and reuse that block in the remaining 11 layers, rather than learning different parameters for each layer among the 12 layers. We can share parameters for the feed-forward layer only/share attention parameters only/share all parameters. The default method in the paper is to share all parameters.

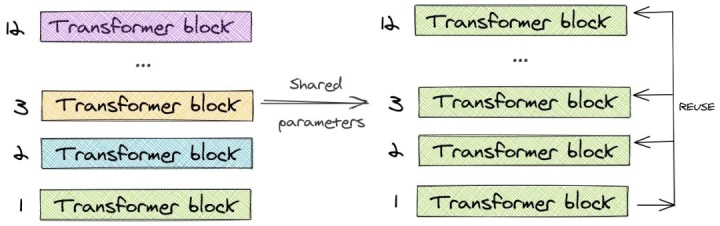
Compared to BERT-base’s 110 million parameters, the ALBERT model with the same number of layers and hidden size only has 31 million parameters. When the hidden size is 128, the impact on accuracy is minimal. The main drop in accuracy is due to the parameter sharing of the feed-forward layer. The impact of sharing attention parameters is minimal.

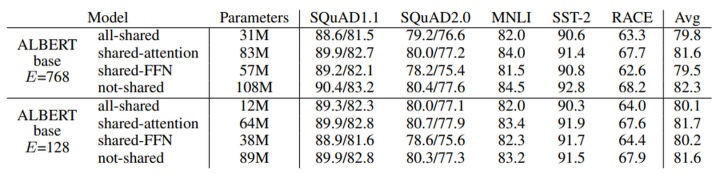
These methods of reducing parameters in ALBERT can also be seen as a form of regularization, helping to stabilize the model and enhance generalization ability.

Since matrix low-rank decomposition and parameter sharing do not significantly affect model performance, we can increase ALBERT’s parameter count, allowing it to use fewer parameters than BERT-large while achieving better performance.

References for this article: