
Looking back at the phrase from 2017, “Attention is all you need”, it truly was a prophetic statement. The Transformer model started with machine translation in natural language processing, gradually influencing the field (I was still using LSTM in my graduation thesis in 2018), and then it swept the entire NLP domain. Especially after BERT came out, everything else was cast aside. After NLP had its influence, it began to radiate to other fields, such as computer vision, where it started to be used more frequently, like in the previous object detection paper.
Undoubtedly, the widespread adoption of the Transformer is closely related to its remarkable flexibility and scalability. Flexibility allows it to handle various tasks, while scalability enables it to fully leverage the ever-growing computational resources. Due to its popularity, researchers have begun to study the Transformer itself from various perspectives.
As mentioned in the previous article from 2020-0713, the research paradigm is:
1) First, experts invent new methods or architectures;
2) Then, with a new hammer, everyone switches to it and starts looking for nails, which is known as low-hanging fruit;
3) Next, when all the easy nails are gone, people start analyzing the hammer itself, noting that while it is large and sturdy, it still has some drawbacks; they begin to think about how to improve it;
4) Finally, new datasets are released for better testing.
Now, everyone is studying and analyzing the hammer itself; looking at this hammer, it seems somewhat similar to something else.
Hey, it looks a bit like CNN
This claim primarily stems from the ICLR 666 paper: On the Relationship between Self-Attention and Convolutional Layers
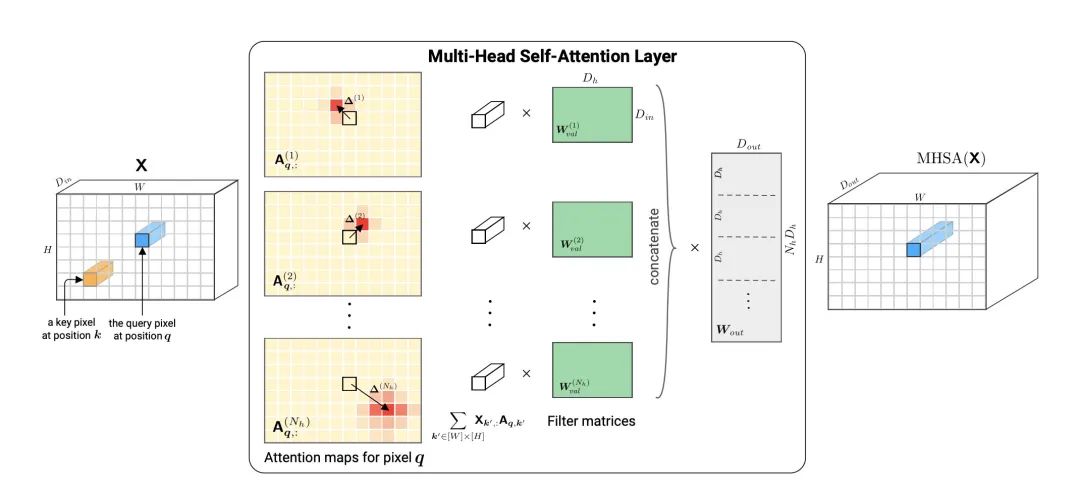
This paper mainly proves that when a multi-head self-attention layer is combined with an appropriate relative position encoding, it can represent any convolutional layer.
The multi-head mechanism allows it to focus on each pixel location in the CNN’s receptive field, so a multi-head self-attention with head count N can simulate a CNN convolution kernel with a receptive field of .
Additionally, relative position encoding is primarily used to ensure the translation invariance property found in CNNs.
Although this paper makes it clear, the first realization of the relationship between CNNs and Transformers did not come from this paper, but rather from reading the Dynamic CNN paper, Pay Less Attention with Lightweight and Dynamic Convolutions. After reproducing Dynamic CNN, I found that some of its properties were quite similar to those of Transformers.
Hey, it also looks a bit like GNN
The main claim comes from this blog: Transformers are Graph Neural Networks (https://graphdeeplearning.github.io/post/transformers-are-gnns/)
First, let’s look at the main structure of GNNs. For a graph with nodes and edges:
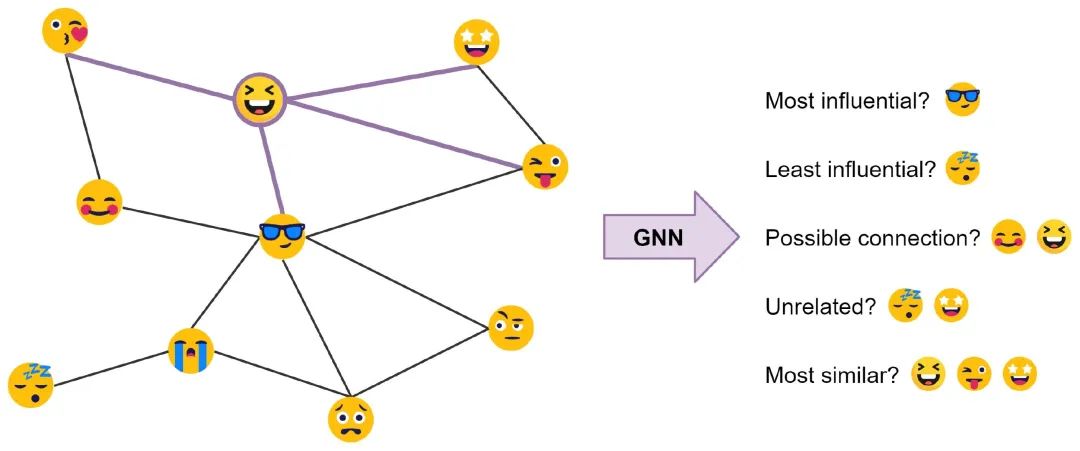
When calculating the feature representation of a node, it updates its representation by collecting features from neighboring nodes through neighborhood aggregation, thereby learning the local structure of the graph. Similar to CNNs, by stacking a few layers, the learning scope can gradually expand to cover the entire graph.
Thus, the basic computational form is represented by the following formula, where and are learned parameters, and is the node being computed, while are the neighboring nodes. In this expression, can be considered an aggregation function that can be implemented in various other ways. Lastly, there is a non-linearity.
The representation as an image is:
At this point, we can represent the self-attention mechanism of Transformers similarly in graph form:
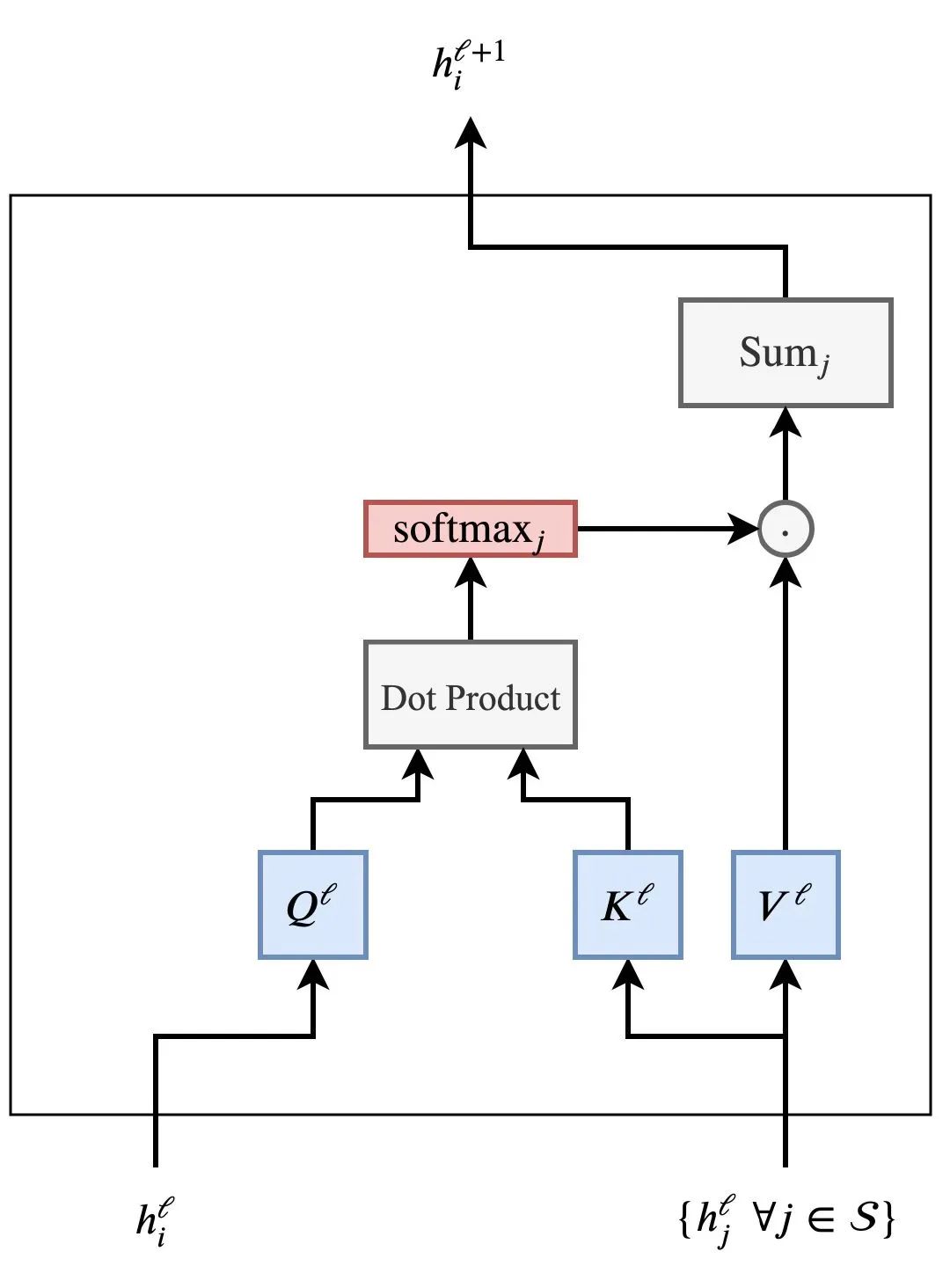
They are quite similar. The difference lies in the fact that the simple aggregation function in the basic GNN has been complicated, transformed into a weighted aggregation based on the attention mechanism, where the calculation process is not merely through learning a matrix but through dot products with neighboring nodes (or through other methods).
Thus, in NLP, the self-attention mechanism can be seen as treating the sentence as a fully connected graph, where each word is adjacent to all other words in the sentence. Consequently, when calculating, all words are considered. This fully connected nature leads to a criticized property of Transformers: as the sentence length increases, the computational complexity grows as O(N^2), which becomes very costly when the sentence is long.
Recently, many papers like Reformer, Linformer, etc., have attempted to address this issue.
For some studies in Transformers that aim for local attention, it is essentially introducing the prior belief that nearby words in a sentence are considered adjacent nodes.
Hey, how does it also look a bit like RNN
Finally, this comes from a recent paper, Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention.
To put it simply, Transformers are RNNs, Q.E.D.
Just kidding, flipping through the paper reveals that the first half does not mention how it resembles RNNs; instead, it discusses how to optimize Transformers to reduce computational complexity to linear. This includes using kernel functions to simplify the attention computation process and replacing Softmax. However, by the end, it becomes clear that these optimizations, especially the kernel function optimization, allow for a similar computation process during causal masking to RNNs.
To summarize, for the general attention form, its formula is as follows:
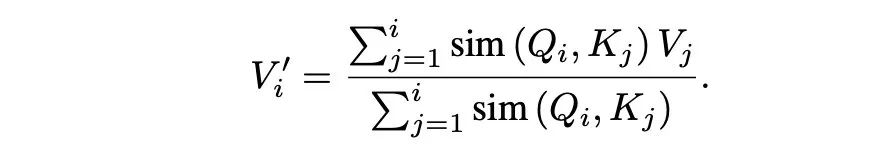
Familiar QKV, where Q and K utilize a similarity (sim) function to calculate a score, which is then divided by the total score to obtain the attention weights, and then values are fetched from V.
Next, using the kernel function , the sim function is processed, and by utilizing the associative property, Q’s computation is factored out:
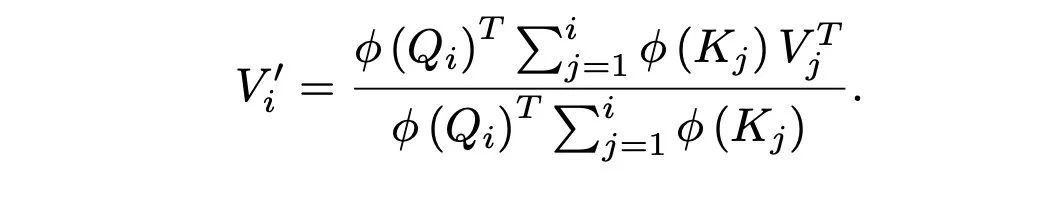 Then, two simplified representations are introduced:
Then, two simplified representations are introduced:
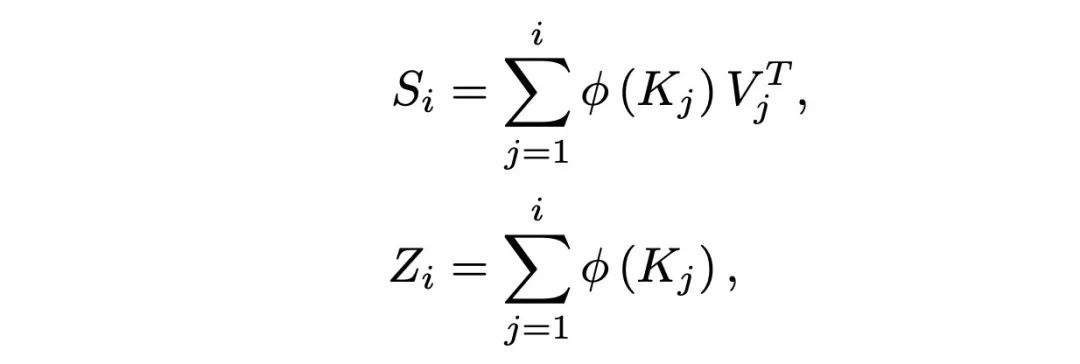 The entire equation transforms into:
The entire equation transforms into:
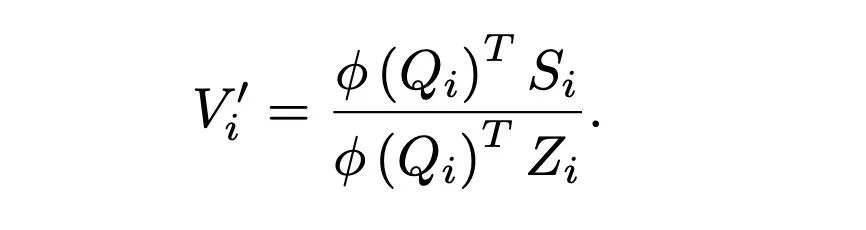
Thus, during causal masking, for S and Z at each time step, previous time step results can be reused, allowing S and Z to be viewed as two hidden states, which can update their states at each time step based on the current input, which is precisely the main idea of RNNs.
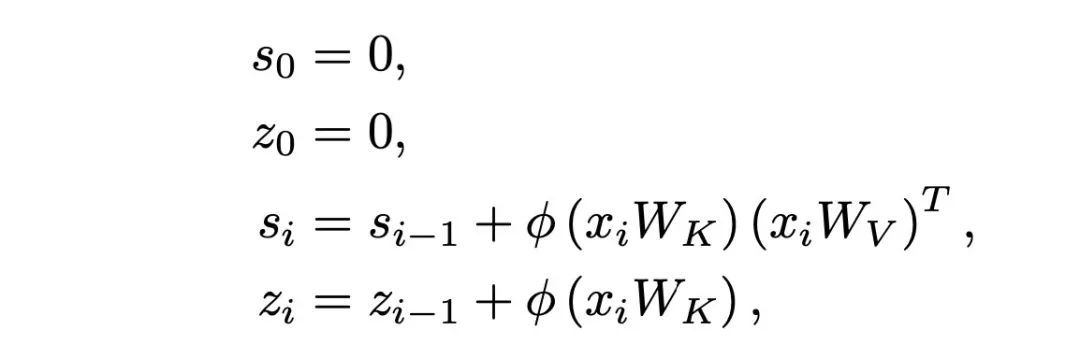
Repository address shared:
Reply "code" in the backend of the machine learning algorithms and natural language processing public account to get access to 195 NAACL + 295 ACL2019 papers with open-source code. The open-source address is as follows: https://github.com/yizhen20133868/NLP-Conferences-Code
Exciting news! The Yizhen Natural Language Processing - Pytorch group has officially been established! There are a wealth of resources in the group; everyone is welcome to join and learn! Please modify your remarks when adding to [School/Company + Name + Direction] For example - Harbin Institute of Technology + Zhang San + Dialogue System. Please avoid adding the account holder for business purposes. Thank you!
Recommended reading:
Exploration of the Few-Shot Dilemma in NLP
Collection of Deep Learning CNN Tricks
Several Review Articles on Multi-Task Learning
