Understanding PyTorch Internals: Insights from Core Developer Edward Z. Yang

Edward Z. Yang, a PhD student at Stanford University and a research engineer at Facebook AI Research, is one of the core developers of the PyTorch open-source project. He gave a talk on the internal mechanisms of PyTorch at the PyTorch NYC meetup on May 14, and this article is an extended version of that talk.

Hello everyone! Today I want to talk about the internal mechanisms of PyTorch.

This talk is aimed at those who have used PyTorch and are interested in contributing but have been deterred by its massive C++ codebase. There’s no need to sugarcoat it: the PyTorch codebase can indeed be daunting at times.

The purpose of this talk is to provide you with a roadmap: to explain the basic conceptual structure of a “tensor library that supports automatic differentiation” and to provide you with some tools and techniques to help you navigate the codebase. I assume you have written some PyTorch before but may not have deeply understood how machine learning software libraries are written.

This talk is divided into two parts: in the first part, I will provide a comprehensive introduction to various concepts of tensor libraries. I will first talk about the tensor data types you know and love, and discuss in detail what this data type can offer, which will help us better understand its internal implementation.

If you are an advanced PyTorch user, you may already be familiar with most of this material. We will also discuss three concepts of “extension points”, layout, device, and dtype, which will guide us in thinking about how to extend tensor classes. During the live talk at the PyTorch NYC meetup, I skipped the slides about autograd, but I will explain some of that here.

The second part will explain the basic details involved in actually writing code with PyTorch. I will tell you how to navigate through autograd code, what code is truly important, and how to benefit others, and I will introduce all the cool tools PyTorch provides for writing kernels.

Concepts

Tensor

A tensor is the core data structure in PyTorch. You may already have a good understanding of what a tensor intuitively represents: a tensor is an n-dimensional data structure containing some scalar type (such as floating-point numbers and integers). We can think of a tensor as being made up of some data, along with some metadata that describes the tensor’s size, the type of elements it contains (dtype), and the device on which the tensor resides (CPU memory? CUDA memory?).

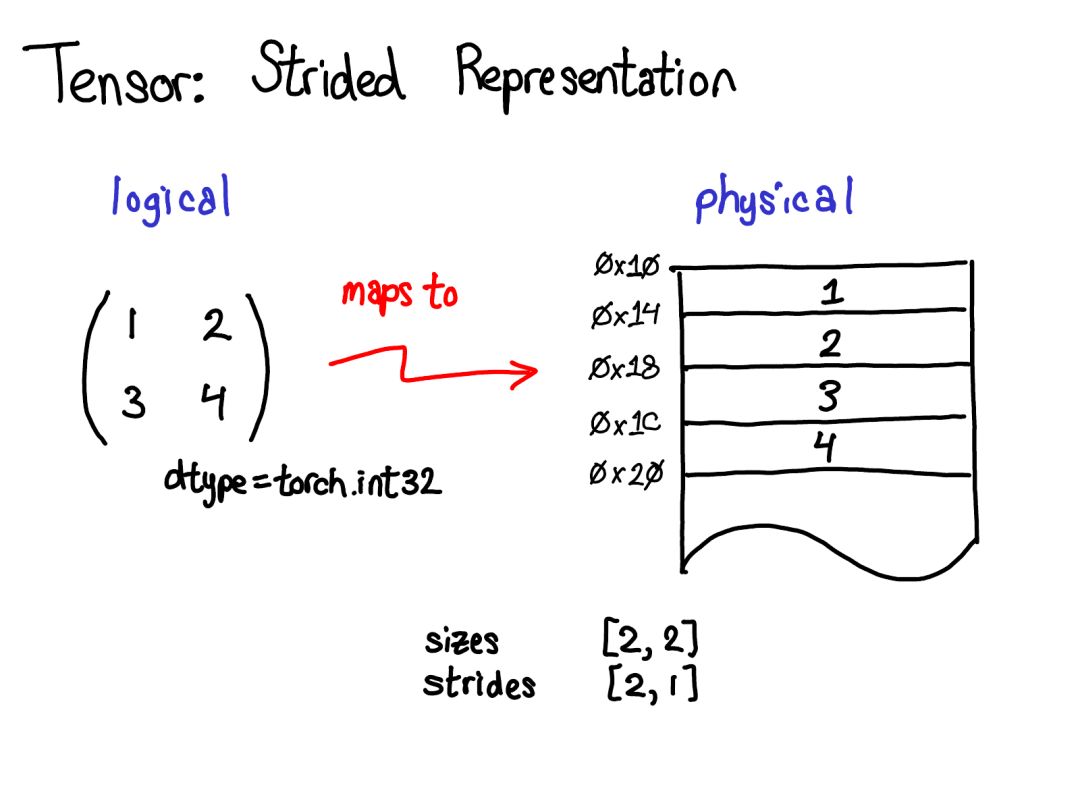
There is also a piece of metadata you may not be as familiar with: stride. Stride is actually one of the most elegant features of PyTorch, so it deserves a bit more discussion.

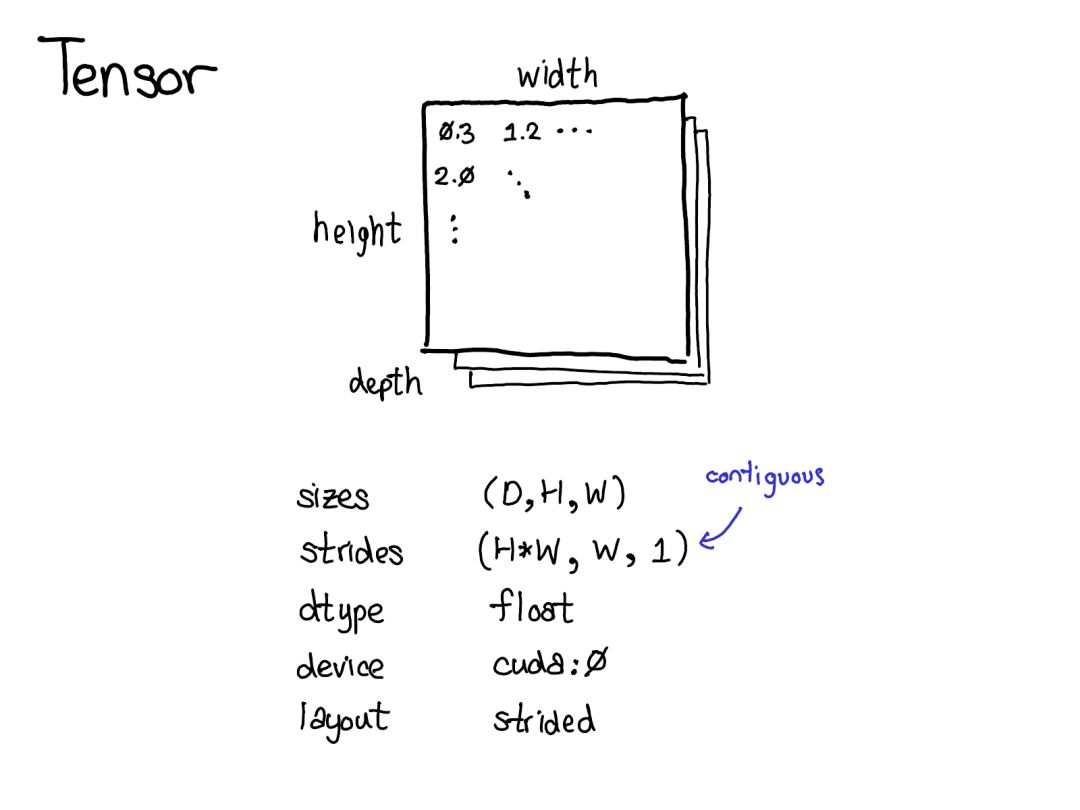
A tensor is a mathematical concept. But to represent it on our computers, we must define some physical representation for it. The most common representation is to place each element of the tensor in memory contiguously (which is also the source of the term “contiguous”), that is, to write each row out to memory as shown above. In the above case, I have specified that the tensor contains 32-bit integers, so you can see that each integer is located at a physical address, with each address being 4 bytes apart from the next. To remember the actual dimensions of the tensor, we must record the scale size as additional metadata.

So how does this image relate to stride?

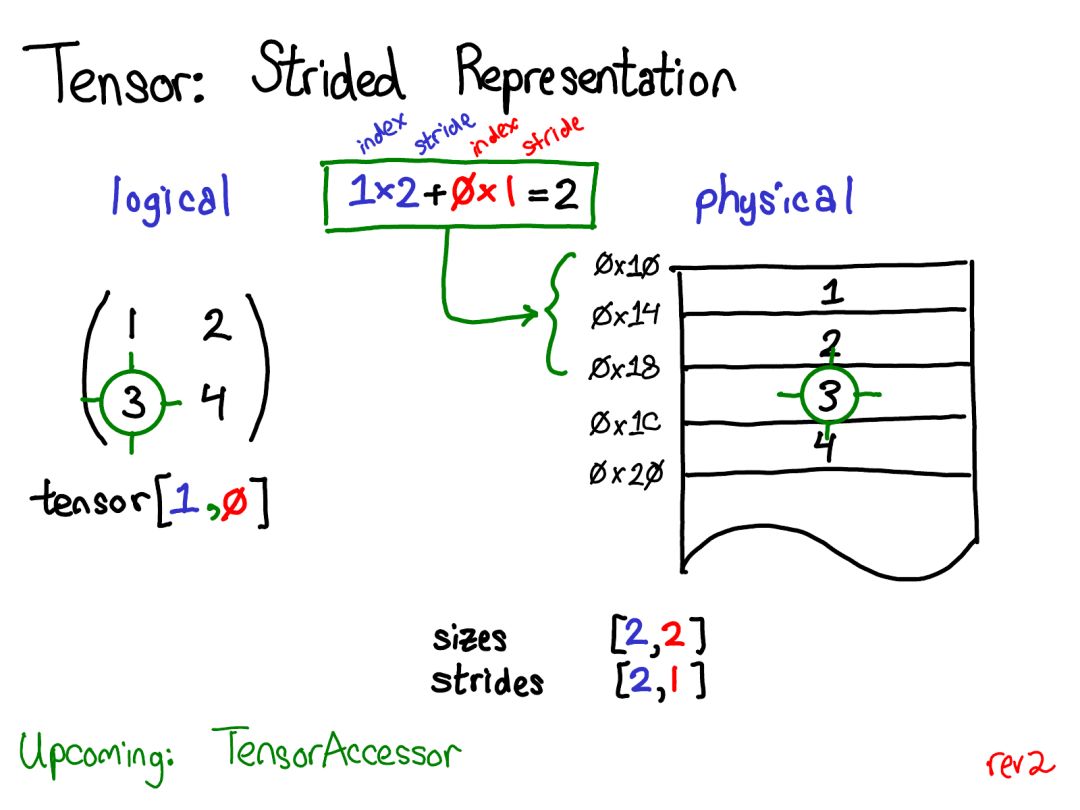
Suppose I want to read the element at tensor position [0,1] in my logical representation. How do I translate this logical position to a physical memory location? Stride allows us to do this: to find the position of any element in a tensor, I multiply each index by its respective stride in that dimension and then sum them all together. In the above image, I used blue to represent the first dimension and red to represent the second dimension, so you can understand the indices and strides in this stride calculation. After performing this summation, I got 2 (zero-indexed); in fact, the number 3 is located just 2 positions below the starting point of this contiguous array.

(Later I will also talk about TensorAccessor, which is a convenience class for handling index calculations. When you use TensorAccessor, you will no longer manipulate raw pointers; these calculations are hidden from you.)

Stride is the fundamental basis on which we explain methods to PyTorch users. For example, suppose I want to extract a tensor representing the second row of the tensor above:

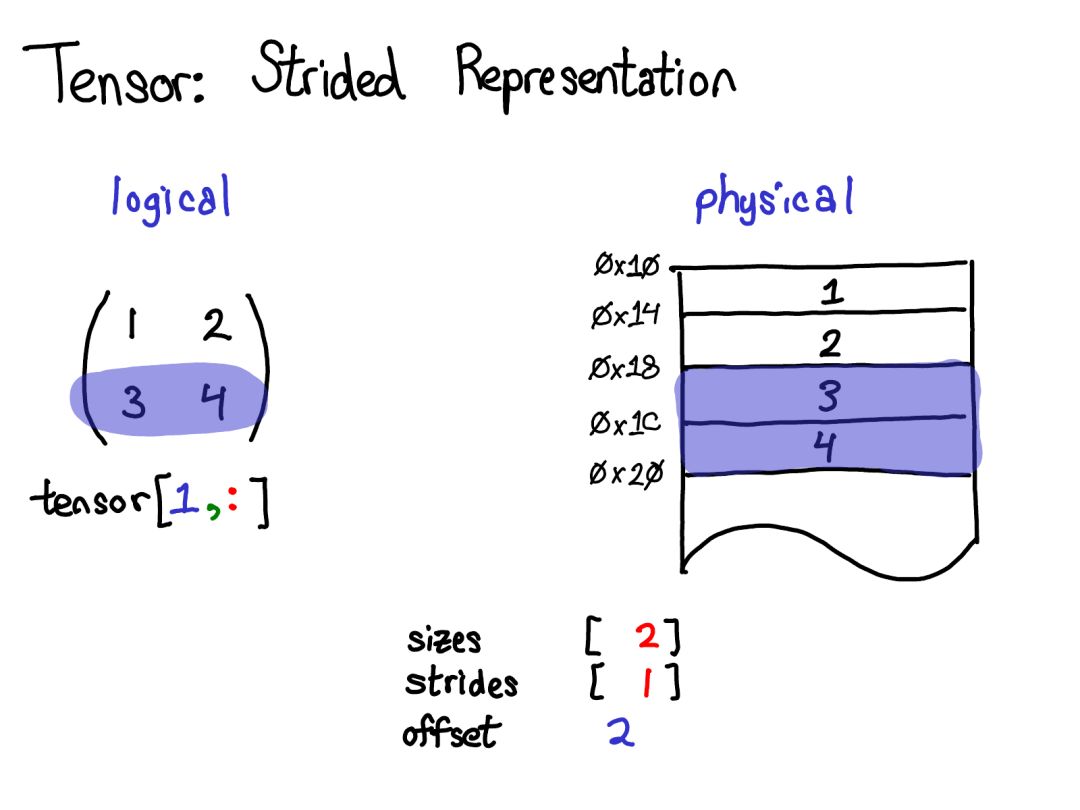
Using advanced indexing support, I can simply write tensor [1, :] to get that row. Importantly: when I do this, I do not create a new tensor; rather, it returns a tensor that is a different view based on the underlying data. This means that if I edit the data in this view, it will reflect in the original tensor.

In this case, understanding how to do this isn’t too difficult: 3 and 4 are located in contiguous memory, and we just need to record an offset that describes that the data of the (logical) tensor is located 2 positions below the top. (Every tensor records an offset, but most of the time it is zero; I omit it in my diagram when it is zero.)

Question during the talk: If I take a slice of a tensor, how do I free the memory of the underlying tensor?

Answer: You have to make a copy of that slice, which breaks its connection to the original physical memory. There’s not much else you can do. Also, if you wrote a substring of a string in Java a long time ago, there’s a similar problem because by default, it doesn’t make a copy, so the substring holds onto (potentially very large) strings. Clearly, Java 7u6 fixed that.

If I want to take the first column, it gets even more interesting:

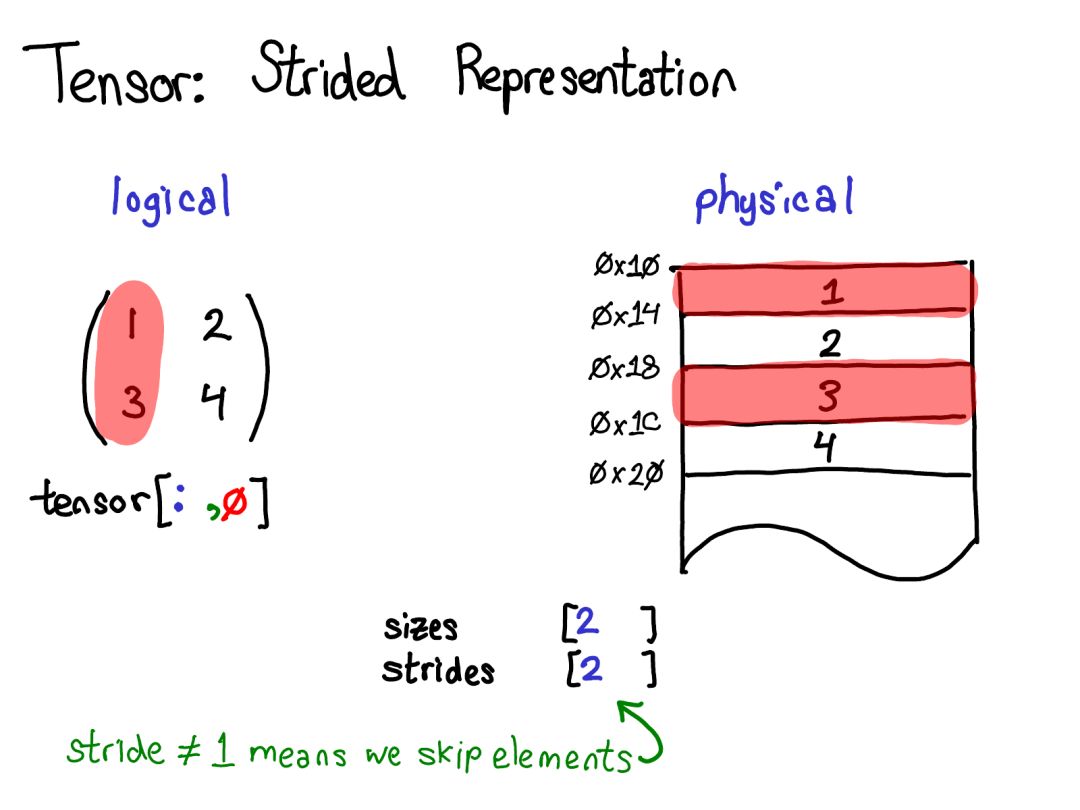
When we look at physical memory, we can see that the elements of that column are not contiguous: there is a gap of one element between them. Stride shines here: we no longer specify the stride between one element and the next as 1, but set it to 2, effectively skipping one element. (By the way, this is why it’s called “stride”: if we think of the index as walking through the layout, the stride specifies how many positions we step forward each time.)

The stride representation actually allows you to represent all kinds of tensor slices; if you want to learn about the various possibilities, please refer to this link.

Now let’s take a step back and think about how we implement this functionality (after all, this is a talk about internal mechanisms). If we can get slices of tensors, it means we must decouple the concept of a tensor (the user-facing concept you know and love) from the actual physical data that stores the tensor’s data (called “storage”):

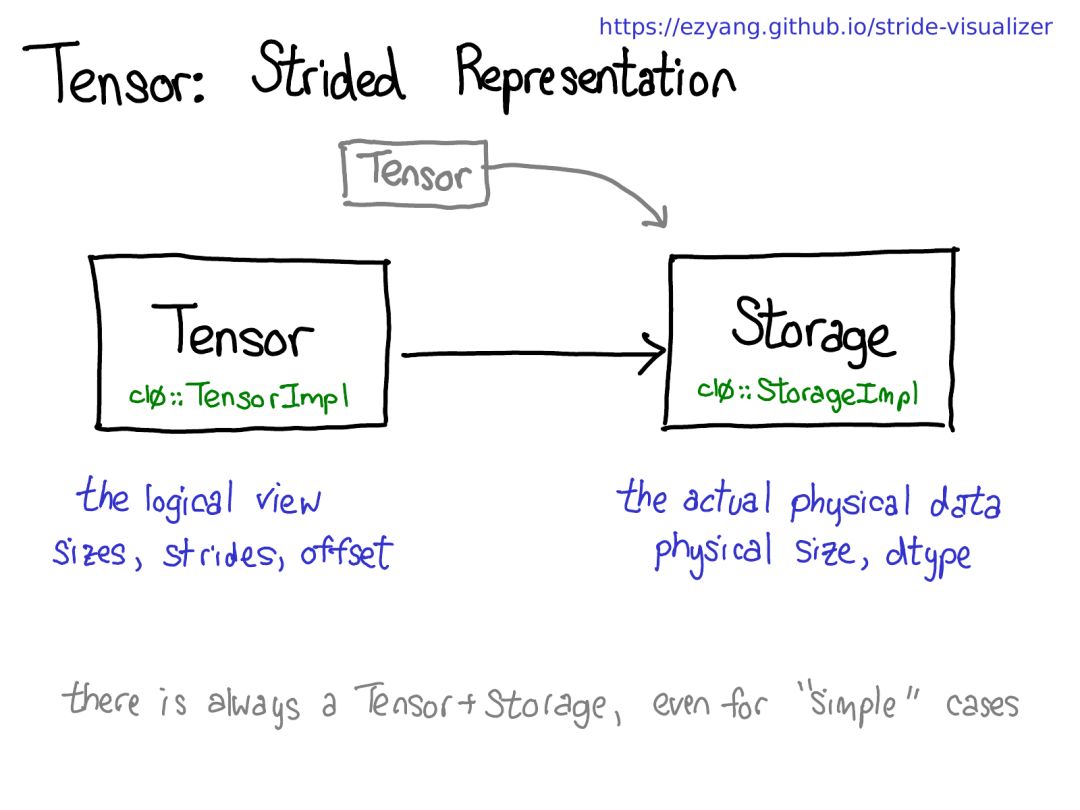
There may be multiple tensors sharing the same storage. The storage defines the tensor’s dtype and physical size, while each tensor also records its own size, stride, and offset, which defines the logical interpretation of the physical memory.

One thing to note: there will always be a tensor-storage pair, even in the “simple” case where storage isn’t really needed (like just allocating a contiguous tensor with torch.zeros(2, 2)).

By the way, we are not interested in that case, but rather in cases where there is a discrete storage concept, just defining a slice as a tensor supported by a base tensor. This is a bit more complex, but it has its benefits: contiguous tensors can achieve a much more direct representation without the indirect hassle caused by storage. Such changes can make PyTorch’s internal representation much closer to Numpy.

We have introduced some data layouts of tensors (some might say that if you properly understand data representation, everything else will naturally fall into place). However, it is still necessary to briefly discuss how tensor operations are implemented. At the most abstract level, when you call torch.mm, two dispatches occur:

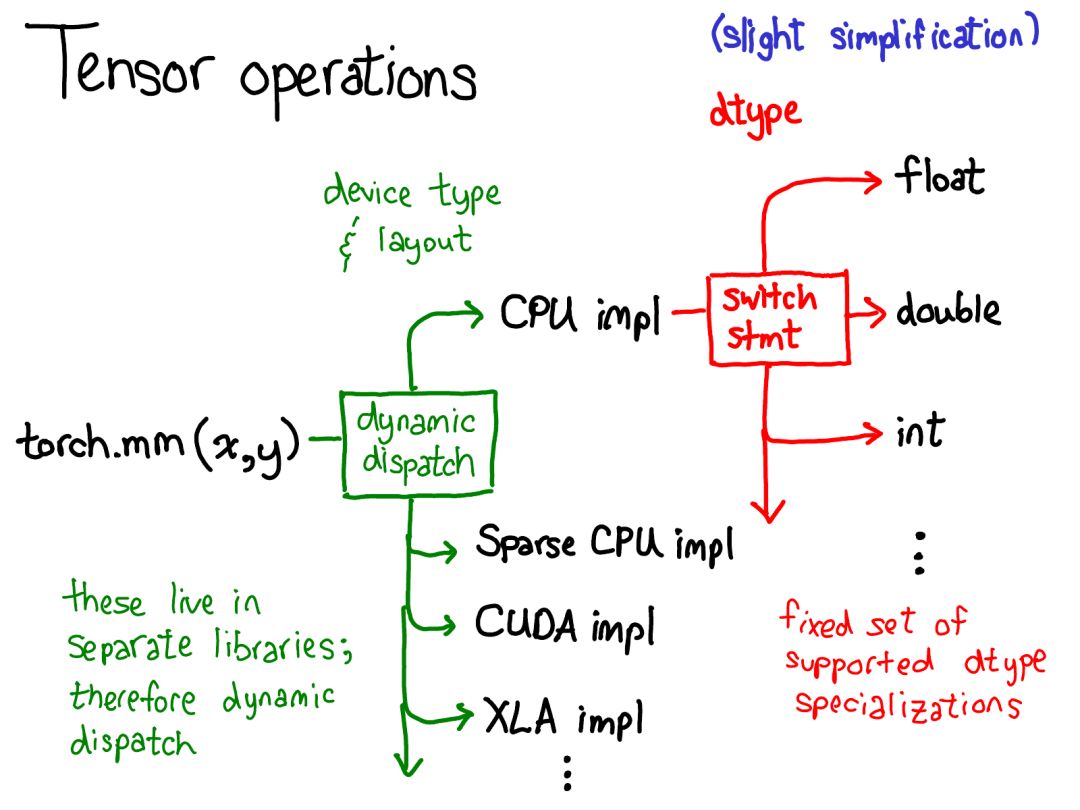
The first dispatch is based on the device type and tensor layout: whether it’s a CPU tensor or a CUDA tensor, whether it’s a tensor with stride or a sparse tensor. This dispatch is dynamic: it’s a virtual function call (the topic of where this virtual function call occurs is the subject of the latter half of this talk).

It should be reasonable to make a dispatch here: the implementation of CPU matrix multiplication is very different from that of CUDA. The reason for dynamic dispatch here is that these kernels may reside in different libraries (like libcaffe2.so or libcaffe2_gpu.so), and you have no choice: if you want to enter a library you don’t have a direct dependency on, you must reach it via dynamic dispatch.

The second dispatch is on the dtype involved. This dispatch is just a simple switch statement targeting any dtype supported by the kernel selection. The reason for dispatching here is also reasonable: CPU code (or CUDA code) is based on float for multiplication, which is different from the code used for int. This indicates that you need to use different kernels for each dtype.

If you want to understand how operators are called in PyTorch, this might be the most important knowledge you should have in mind. We will return to this when we delve deeper into the code.

Since we have talked about tensors, I also want to spend some time discussing tensor extensions. After all, apart from dense CPU floating-point tensors, there are many other types of tensors, such as XLA tensors, quantized tensors, MKL-DNN tensors; and for a tensor library, there is one more thing to think about: how to accommodate these extensions?

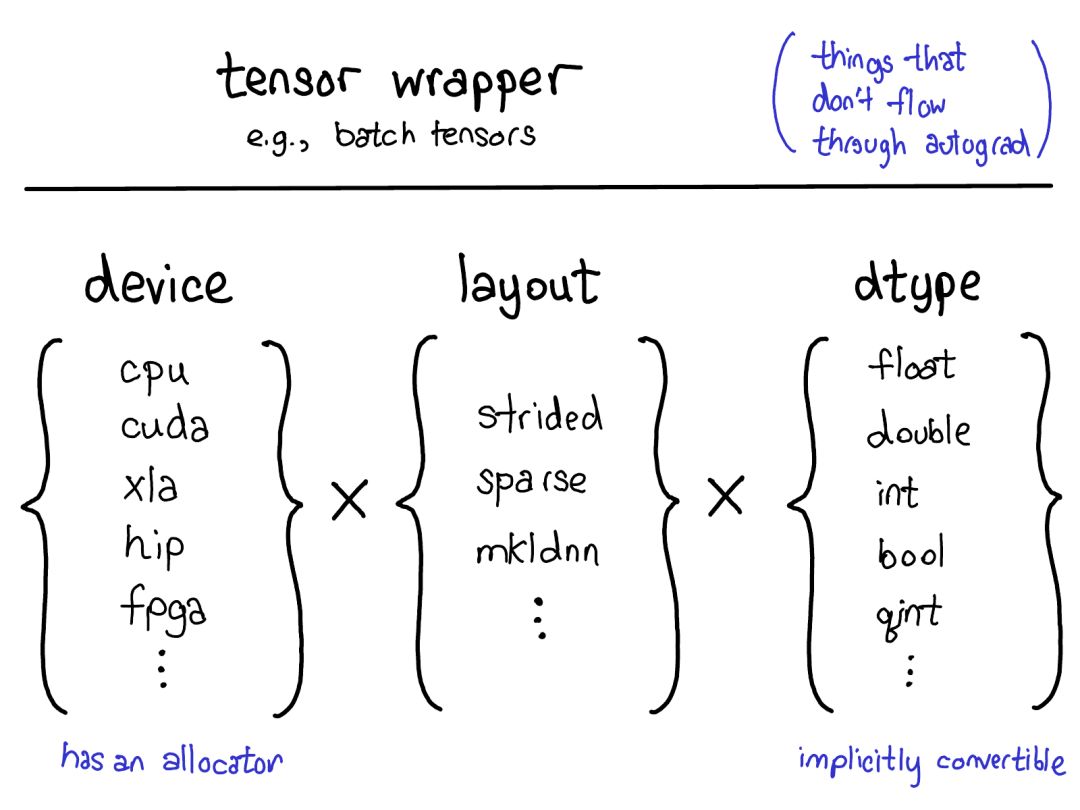
Our current model for extensions provides four extension points for tensors. First, there are three parameters that independently determine the tensor type:

• device: describes the physical memory where the tensor is actually stored, such as on a CPU, NVIDIA GPU (cuda), AMD GPU (hip), or TPU (xla). The different characteristics of devices have their own allocators, which cannot be used for other devices.

• layout: describes how to logically interpret the physical memory. The most common layout is strided tensors, but the layout for sparse tensors is different, involving a pair of tensors, one for indexing and one for data; MKL-DNN tensor layouts are even more peculiar, such as blocked layout, which cannot be represented by stride alone.

• dtype: describes the type of data actually stored in each element of the tensor, such as floating-point numbers, integers, or quantized integers.

If you want to add an extension to PyTorch tensors, you should think about which of these parameters you want to extend. The Cartesian product of these parameters defines all the possible tensors you can obtain. Now, not all of these combinations have kernels (who has kernels for sparse quantized tensors on FPGA?), but in principle, this combination can make sense, so we should at least support expressing it.

There’s one last way to add “extensions” to the functionality of a tensor, which is to write a wrapper class around the PyTorch tensor of the target type you can implement. This might sound obvious, but sometimes people go off to extend those three parameters when they only need to create a wrapper class. A significant advantage of a wrapper class is that the development results can completely not affect the original type (out of tree).

When should you write a tensor wrapper rather than extending PyTorch itself? The key indicator is whether you need to pass this tensor through the autograd backpropagation process. For example, this indicator tells us that sparse tensors should be a real tensor extension, rather than just a Python object containing an index and value tensor: when performing optimizations on networks involving embeddings, we want to embed generating sparse gradients.

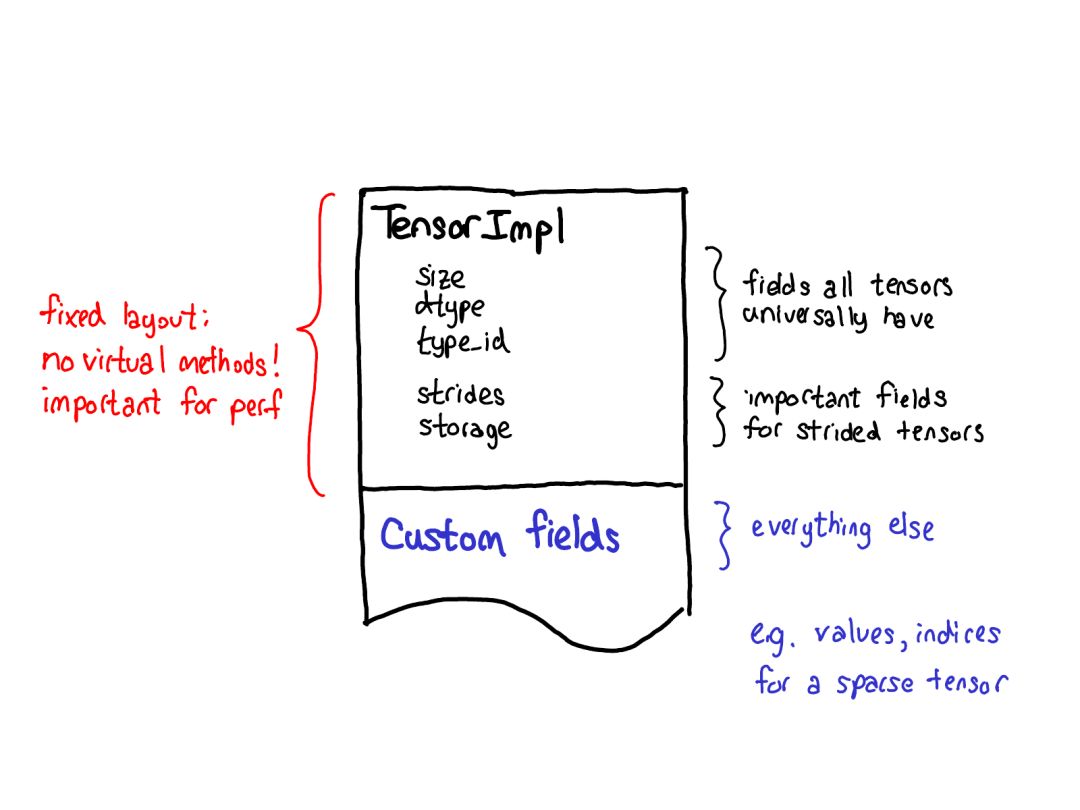
Our concept of extensions will also affect the data layout of the tensor itself. For our tensor structure, one thing we really want is a fixed layout: we don’t want basic operations (this saying is common), like “what is the size of a tensor?” to request virtual dispatch.

So when you look at the actual layout of a tensor (defined as the TensorImpl structure), you will see a common prefix for all fields—we think everything similar to “tensor” will have it; and there are some fields that only really apply to strided tensors, but they are also important, so we keep them in the main structure; then custom fields can be completed on top of each tensor. For instance, sparse tensors can store their indices and values in this suffix.

Autograd

I have explained tensors, but if PyTorch only had this trick, it would just be a clone of Numpy. The remarkable feature of PyTorch is its provision of automatic differentiation for tensors since its initial release (now we also have cool features like TorchScript, but back then, it was just this!).

What is automatic differentiation? It is the mechanism responsible for running neural networks:

…… and filling in the code that is missing for actually calculating the gradients of your network:

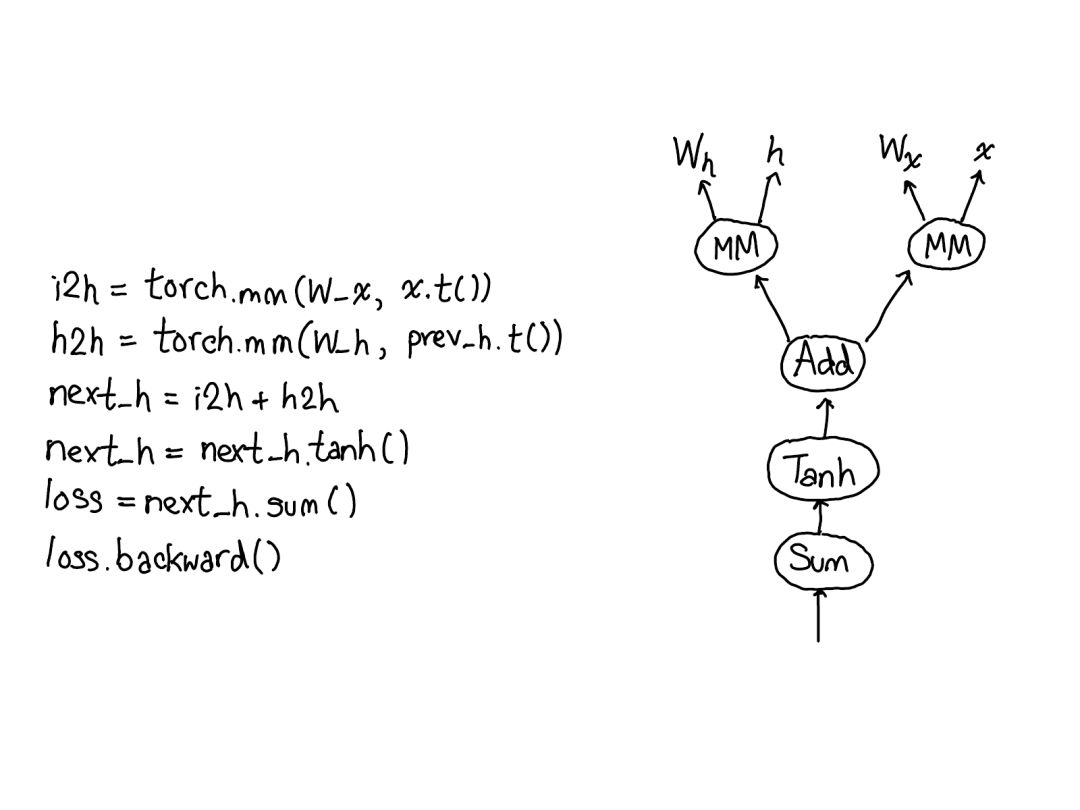
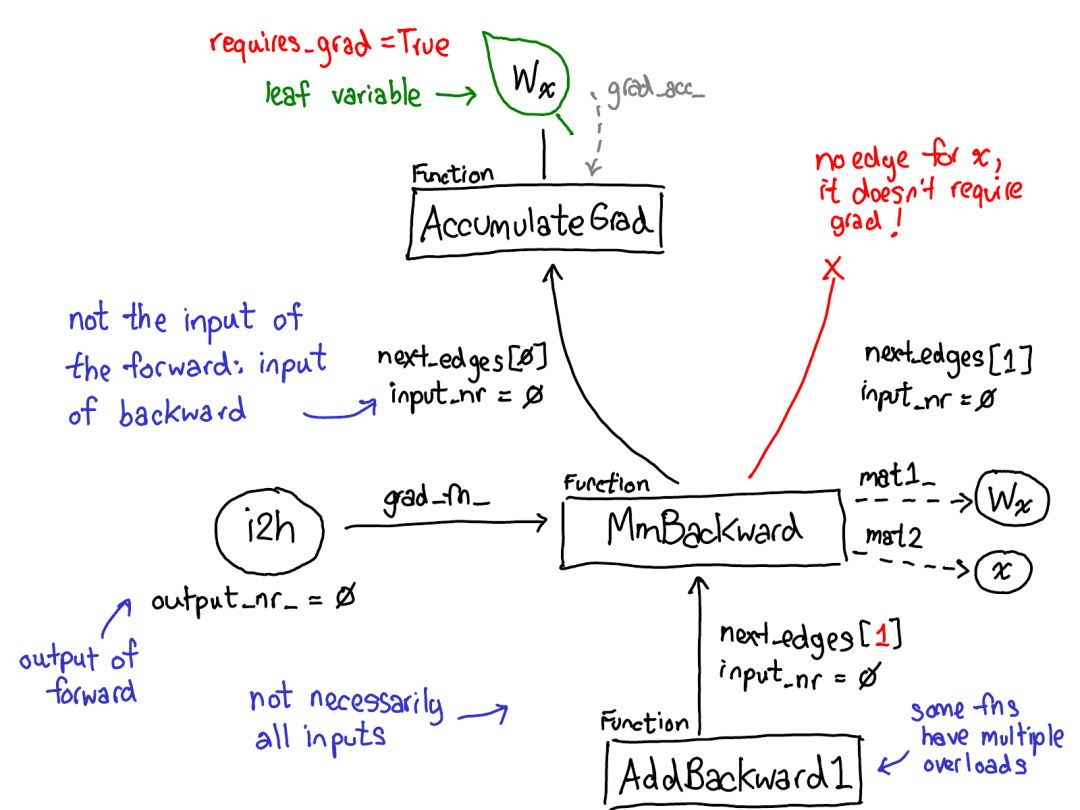
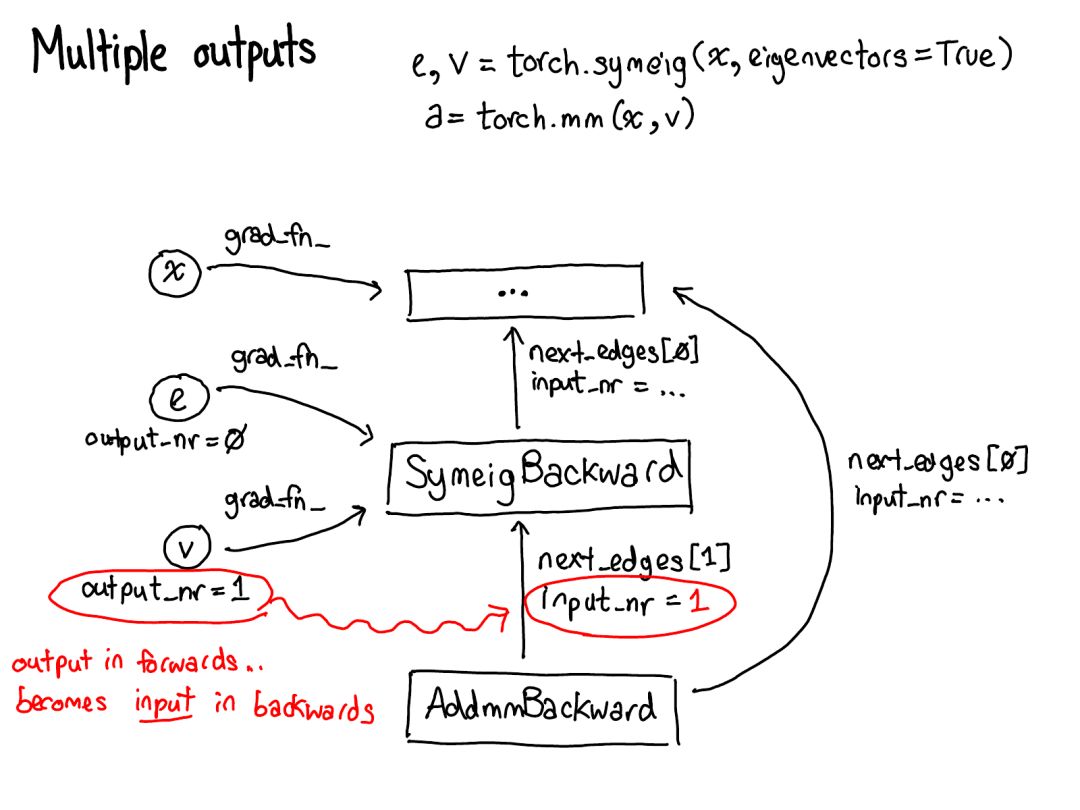
Take a moment to look at this diagram. There’s a lot to interpret, let’s take a look:

• First, turn your attention to the red and blue variables. PyTorch implements reverse-mode automatic differentiation, which means we can “walk backwards” through the forward computation to efficiently compute gradients. You can see this in the variable names: at the bottom of the red section, we compute the loss; then in the blue part of this program, the first thing we do is compute grad_loss. The loss is computed based on next_h2, allowing us to compute grad_next_h2. Technically, the variables we added grad_ to are not actually gradients; they are actually left-multiplied by the Jacobian matrix of a vector, but in PyTorch, we simply call them grad, and basically everyone knows what that means.

• If the structure of the code remains the same, the behavior does not: every line from the forward is replaced by a different computation, representing the derivative of the forward operation. For example, the tanh operation is translated into the tanh_backward operation (these two lines are connected by a gray line on the left side of the diagram). The inputs and outputs of forward and backward operations are swapped: if the forward operation yields next_h2, the backward operation takes grad_next_h2 as input.

The significance of autograd lies in executing the computations described in this diagram without actually generating this source. PyTorch autograd does not perform source-to-source transformations (although PyTorch JIT does know how to perform symbolic differentiation).

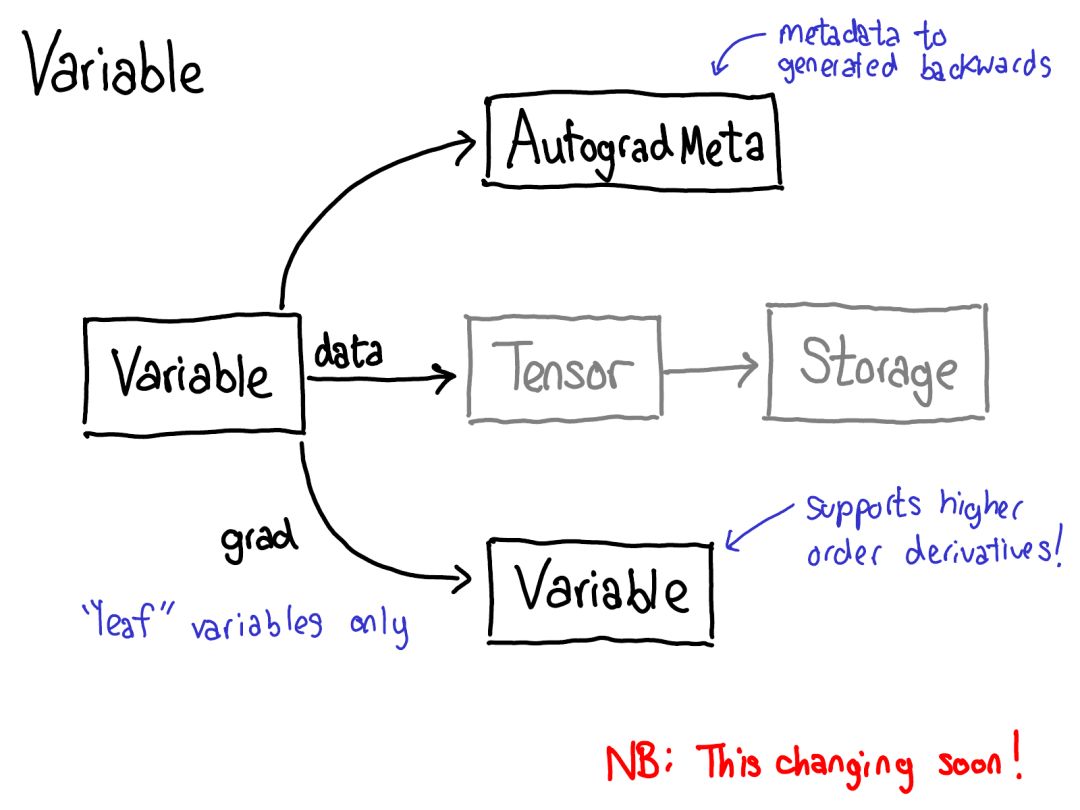
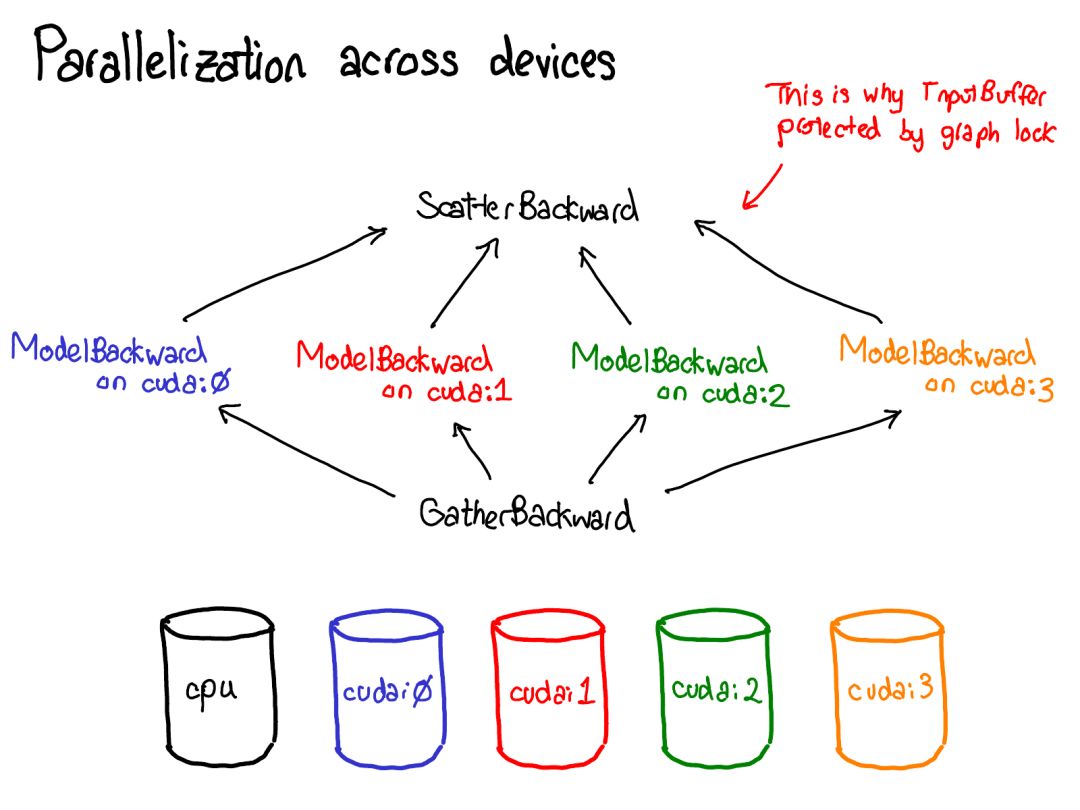
To achieve this, we need to store more metadata when performing operations on tensors. Let’s adjust our diagram of tensor data structures: now it’s not just a tensor pointing to storage; we also have a variable wrapping this tensor, and it also stores more information (AutogradMeta), which is required by users when they call loss.backward() to execute autograd in their PyTorch scripts.

The content of this slide will soon be outdated. Will Feng is pushing for the fusion of variables and tensors in C++ after simply merging the PyTorch front-end port: https://github.com/pytorch/pytorch/issues/13638.

We also need to update the diagram above about dispatching:

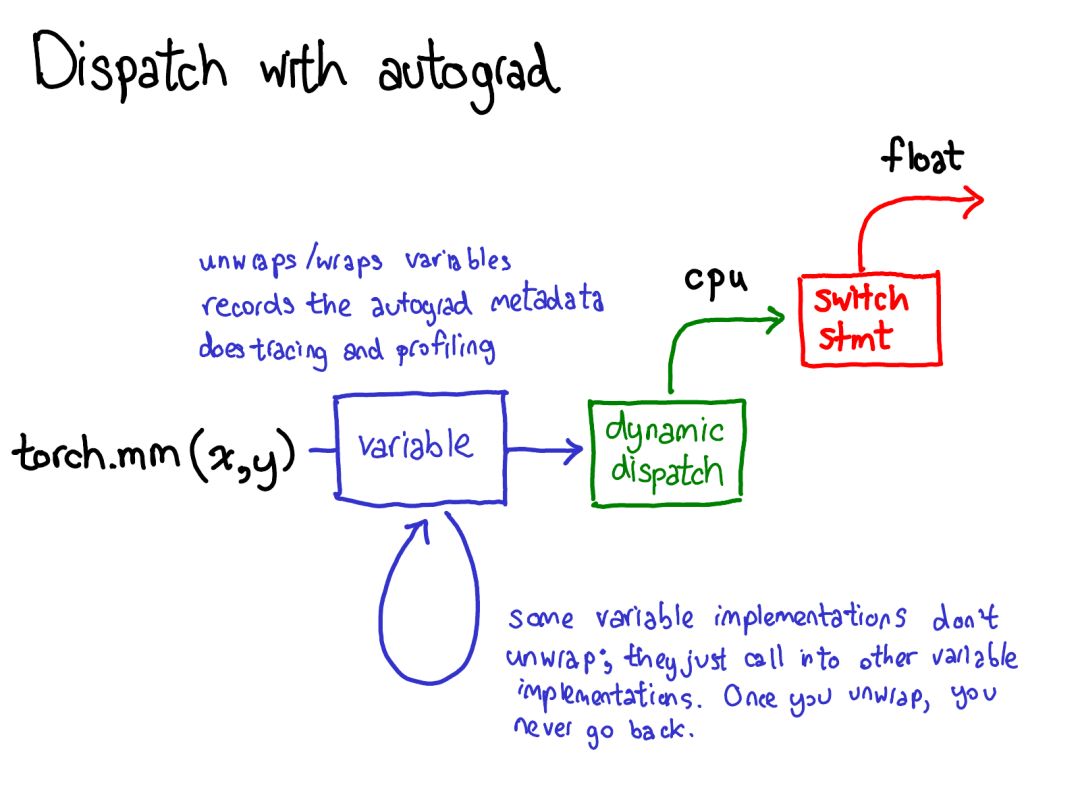
Before we dispatch to the CPU or CUDA implementation, there is another dispatch on the variable, which is responsible for unwrapping the variable, calling the underlying implementation (green), and then rewrapping the result into the variable and recording the necessary autograd metadata for the backward process.

Some implementations do not unwrap; they simply call other variable implementations. So you may need to spend some time in the variable universe. But once you unwrap and enter the non-variable tensor universe, you reach the end; you no longer need to return to the variable (unless returning from your function).

I skipped the following seven slides during my talk in New York. The text introduction to them will take some time.

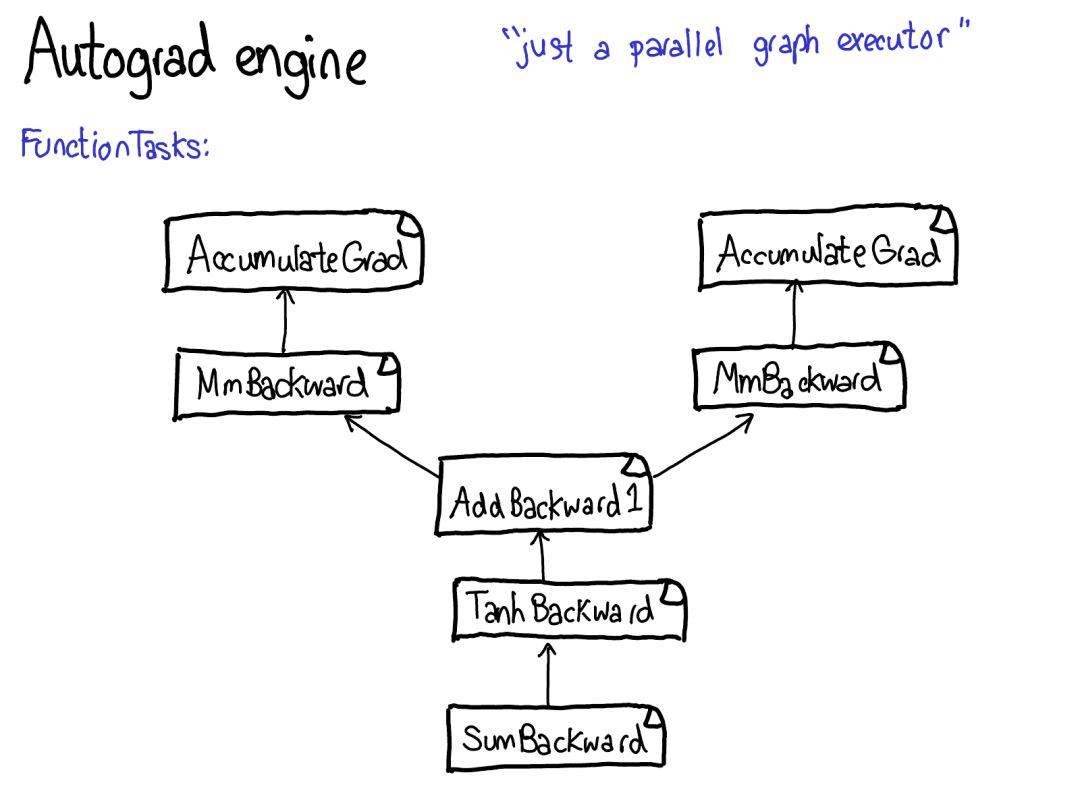
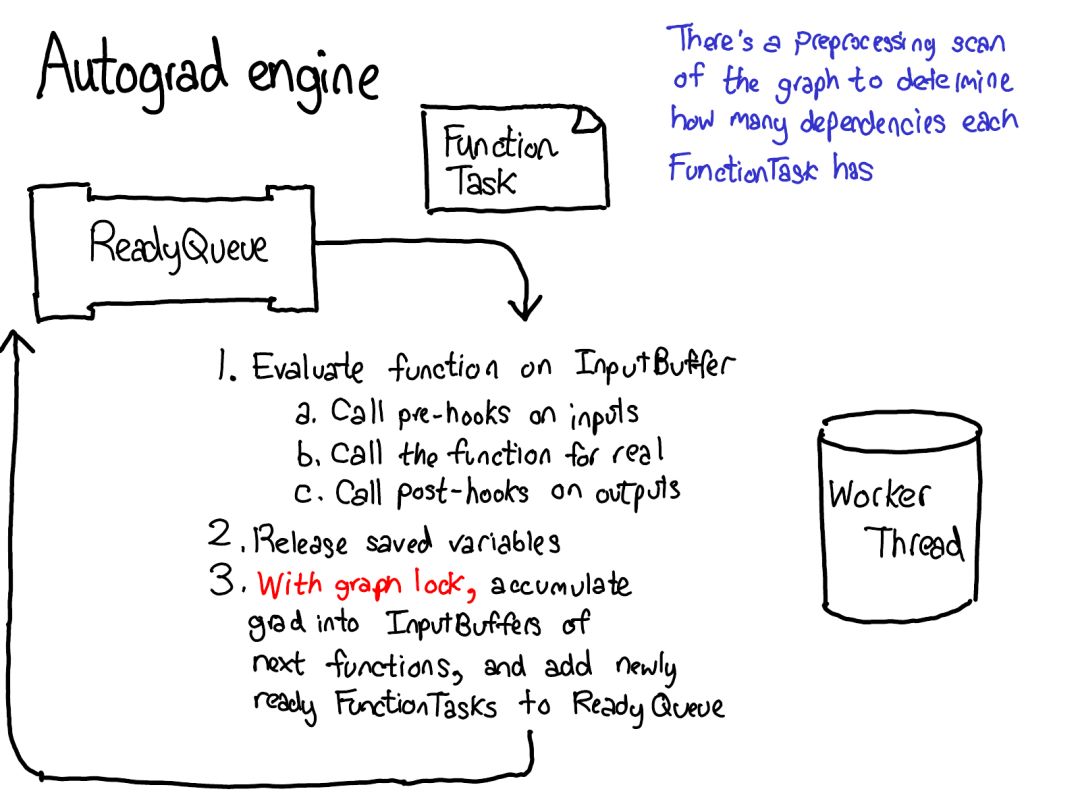
Engineering Development

Having discussed concepts, let’s look at the code.

Finding Your Path

PyTorch has a large number of folders, with a very detailed description of them in the CONTRIBUTING.md document, but in practice, you only need to know 4 directories:

• First, torch/ contains the actual Python modules you are familiar with: the ones you import and use. These are Python code and easy to manipulate (just modify and see the results). However, if you go too deep…

• torch/csrc/: implements the C++ code that you might refer to as the PyTorch frontend. In more descriptive terms, it implements the binding code that converts between Python and C++; it also contains some quite important parts of PyTorch, such as the autograd engine and JIT compiler. It also includes C++ frontend code.

• aten/: this stands for “A Tensor Library” (named by Zachary DeVito), and is a C++ library that implements tensor operations. If you check where some kernel code is located, it is likely in ATen. ATen itself is divided into two operator areas: “native” operators (the modern C++ implementation of operators) and “legacy” operators (TH, THC, THNN, THCUNN), which are legacy C implementations. The legacy operators are the bad part; if possible, do not spend too much time on them.

• c10/: this is a pun on “Caffe2” and “A”Ten” and contains the core abstractions of PyTorch, including the actual implementations of tensors and storage data structures.

Finding code requires looking in many places; we should simplify the directory structure, that’s it. If you want to study operators, you should spend time on aten.

Let’s see how these codes are separated in practice:

When you call a function like torch.add, what happens? If you remember our discussion about dispatching, you should already have these basics in your mind:

• We must convert from the Python realm to the C++ realm (Python argument parsing).

• We handle variable dispatch (VariableType—Type, by the way, has no special relation to programming language types; it’s just a little tool for performing dispatch).

• We handle device type/layout dispatch (Type).

• We have the actual kernel, which is either a modern native function or a traditional TH function.

Each of these steps corresponds to some code. Let’s cut through this jungle.

Our starting landing point in the C++ code is a C implementation of a Python function, which we have seen on the Python side, like torch._C.VariableFunctions.add. THPVariable_add is one such implementation.

For these codes, one important point is that these codes are automatically generated. If you search in the GitHub repository, you won’t find them because you must actually build PyTorch to see them. Another important point is that you don’t need to deeply understand what these codes are doing; you should quickly browse them to know their functionality.

I have highlighted the most important parts in blue: you can see that a PythonArgParser class is used to extract C++ objects from Python args and kwargs; then we call a dispatch_add function (red inline); this releases the global interpreter lock and then calls a regular old method on the C++ tensor itself. On its way back, we rewrap the returned Tensor into a PyObject.

(There’s an error in the slide here: I should explain the variable dispatch code. I haven’t fixed it yet. Some magical things happened, so…)

When we call the add method on the Tensor class, virtual dispatch has not yet happened. Instead, I have an inline method that calls an inline method that calls a virtual method on the “Type” object. This method is a real virtual method (this is why I say Type is just a “little tool” for implementing dynamic dispatch).

In this specific case, this virtual call dispatches to the implementation of add on a class called TypeDefault. This just happens because we have the same add implementation for all device types (CPU and CUDA); if we had different implementations, we might end up with something like CPUFloatType::add. It is this implementation of the virtual method that ultimately leads us to the actual kernel code.

It is also hoped that this slide will soon be outdated; Roy Li is researching using another mechanism to replace Type dispatch, which will better support PyTorch on mobile.

It’s worth emphasizing again that all this code is automatically generated until we reach the kernel.

The road is winding; once you can grasp the direction, I suggest you jump directly to the kernel section.

Writing Kernels

PyTorch provides a wealth of useful tools for those looking to write kernels. In this section, we will learn about some of them. But first, what does writing a kernel require?

We generally consider kernels in PyTorch to consist of the following parts:

• First, some metadata about the kernel we need to write, which aids code generation and allows you to acquire all the bindings with Python without writing a single line of code.

• Once you reach the kernel, you have passed the device type/layout dispatch. The first thing you need to write is error checking to ensure that the input tensors have the correct dimensions. (Error checking is really important! Don’t skimp on it!)

• Next, we typically need to allocate the result tensor that we will write to.

• It’s time to write the kernel. Now you should do the second dtype dispatch to jump to the dtype-specific kernel for each dtype it operates on. (You shouldn’t do this too early, or you’ll just be uselessly copying code that looks the same in any case.)

• Most high-performance kernels require some form of parallelization so that they can take advantage of multi-CPU systems. (CUDA kernels are “implicitly” parallelized, as their programming model is built on large-scale parallelization.)

• Finally, you need to read the data and perform the calculations you want!

In the following slides, I will introduce the tools in PyTorch that can help you achieve these steps.

To fully leverage PyTorch’s code generation capabilities, you need to write a schema for your operator. This schema can provide mypy-style types for your function and control whether to generate bindings for methods or functions on tensors. You can also tell the schema which implementation of your operator to call for a given device-layout combination.

For more information on this format, please refer to: https://github.com/pytorch/pytorch/blob/master/aten/src/ATen/native/README.md.

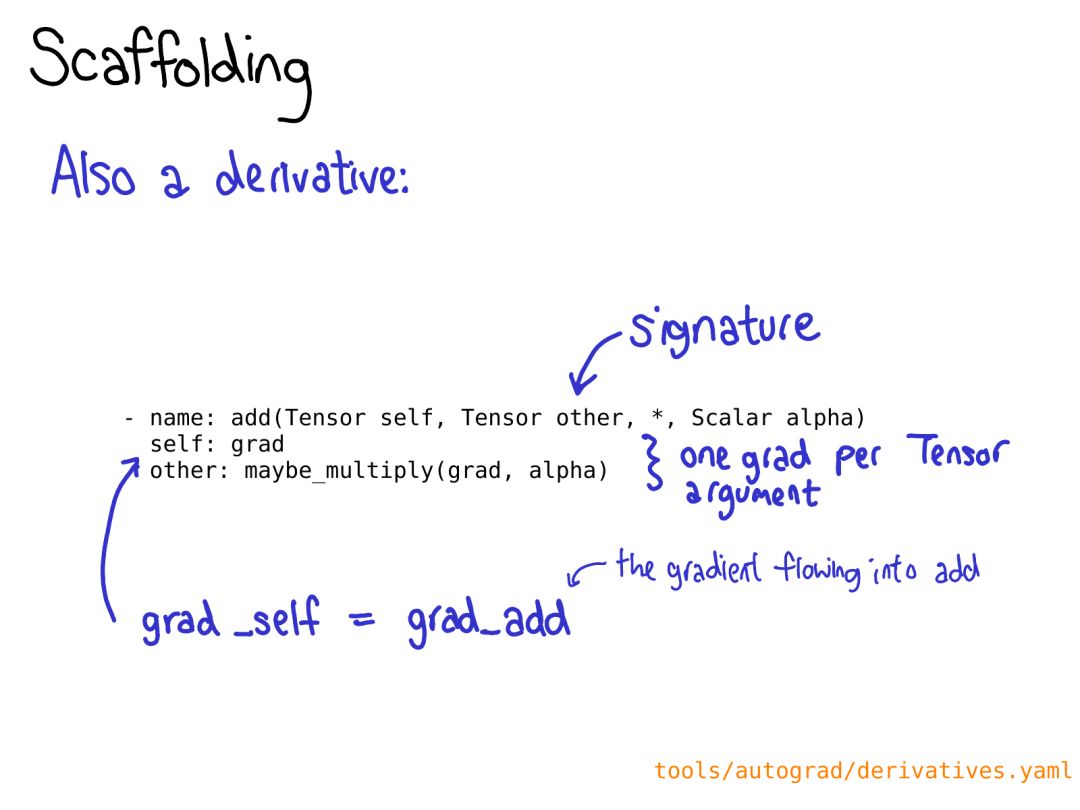
You may also need to define a derivative for your operation in derivatives.yaml.

Error checking can be done at the low-level API or through the high-level API. The low-level API is just a macro TORCH_CHECK, which takes a boolean and any number of parameters that form an error string to conclude whether that boolean is true.

This macro has a nice feature: you can mix strings with non-string data; each item is formatted using their operator<< implementation, and most important data types in PyTorch have an operator<< implementation.

The high-level API allows you to avoid repeatedly writing duplicate error messages. Its method works by first wrapping each tensor as TensorArg, which contains information about where the tensor comes from (like its parameter name). Then it provides some pre-packaged functions for checking various properties; for example, checkDim() tests whether the tensor’s dimension is a fixed value. If not, that function provides a user-friendly error message based on the TensorArg metadata.

When writing operators in PyTorch, one important thing is that you often need to register three operators: abs_out (which operates on a pre-allocated output that implements the out= keyword argument), abs_ (which operates in-place), and abs (which is just the ordinary old functional version of an operator).

Most of the time, abs_out is the real mainstay, while abs and abs_ are just weak wrappers around abs_out; but sometimes you can also write specialized implementations for each case.

To perform dtype dispatching, you should use the AT_DISPATCH_ALL_TYPES macro. This will obtain the dtype of the tensor you want to dispatch on and also specify a lambda for each dtype that can be dispatched from that macro. Generally, this lambda just calls a template helper function.

This macro not only “executes dispatching” but also determines the dtypes that your kernel will support. Thus, this macro actually has quite a few versions that allow you to select different subsets of dtypes to generate specific results. Most of the time, you just need AT_DISPATCH_ALL_TYPES, but also keep an eye out for cases where you may need to dispatch other types.

On the CPU, you usually need to parallelize your code. In the past, this was often done by directly adding OpenMP pragmas to your code.

Sometimes, you really have to access the data. PyTorch provides quite a few options for this.

• If you just want to get the value at a specific position, you should use TensorAccessor. A tensor accessor is like a tensor, but it hardcodes the tensor’s dimensions and dtype as template parameters. When you retrieve an accessor, like x.accessor();, we perform a runtime check to ensure the tensor is indeed of this format; but after that, no checks are performed for each access. Tensor accessors handle strides correctly, so you’d better use them instead of raw pointer access (unfortunately, many traditional kernels do this).

• If you are writing some operator with very regular element access, like pointwise operations, it’s much better to use far higher-level abstractions, like TensorIterator. This helper class automatically handles broadcasting and type promotion, which is quite handy.

• To get real speed on the CPU, you might need to write your kernel using vectorized CPU instructions. We also have helper functions for this! The Vec256 class represents a scalar vector and provides methods to perform vectorized operations on them at once. Then, binary_kernel_vec and other helper functions allow you to easily run vectorized operations and then end those that cannot be easily converted to vector instructions with ordinary old instructions. This infrastructure can compile your kernel multiple times under different instruction sets and then runtime test what instructions your CPU supports, using the best kernel in those cases.

Many kernels in PyTorch are still written in the traditional TH style. (By the way, TH stands for TorcH. It’s a great acronym, but unfortunately, it’s been tainted; if you see TH in the name, consider it traditional.) What does traditional TH style mean?

• It’s written in a C-style, with little or no use of C++.

• Its refcounting is manual (using an artificial call to THTensor_free to lower your refcounts when you finish using a tensor).

• It’s located in the generic/ directory, meaning we actually compile this file many times but use different #define scalar_t.

This code is quite crazy, and we hate revisiting it, so please don’t add more. If you want to write code but know little about kernel writing, one useful thing you can do is port some TH functions to ATen.

Workflow Efficiency

Finally, I want to talk about workflow efficiency on PyTorch. If the massive C++ codebase of PyTorch is the first roadblock preventing people from contributing to PyTorch, your workflow efficiency is the second. If you want to develop C++ with Python habits, it can be quite painful: recompiling PyTorch takes a lot of time, and it also takes a lot of time to know whether your changes are effective.

How to work efficiently might be worth a talk in itself, but this slide summarizes some of the most common anti-patterns I’ve seen some people complain about: “Developing PyTorch is hard.”

• If you edit a header, especially one that is included by many source files (especially when included by CUDA files), expect long rebuild times. Try to only edit cpp files and be cautious when editing headers!

• Our CI is a very good zero-setup way to test whether modifications are effective. But you might have to wait an hour or two for feedback. If you’re making a change that will require a lot of experimentation, take some time to set up a local development environment. Similarly, if you encounter hard debug issues on a specific CI configuration, set it up locally. You can download and run the Docker image locally: https://github.com/pytorch/ossci-job-dsl.

• The contribution guide explains how to set up ccache: https://github.com/pytorch/pytorch/blob/master/CONTRIBUTING.md#use-ccache; this is strongly recommended, as it can help you avoid a lot of recompilation when editing headers by giving you a lucky break. This can also help you cover up our build system’s flaws when we recompilation when we shouldn’t have.

• Lastly, we will have a lot of C++ code. If you are building on a powerful server with CPU and RAM, it will be a pleasant experience. Notably, I do not recommend performing CUDA builds on a laptop. Building CUDA is very, very slow, and laptops often lack the performance to complete it quickly.

Get Involved!

That’s our whirlwind tour of PyTorch kernels! Much has been omitted; but I hope the descriptions and explanations here can at least help you digest a significant portion of its codebase.

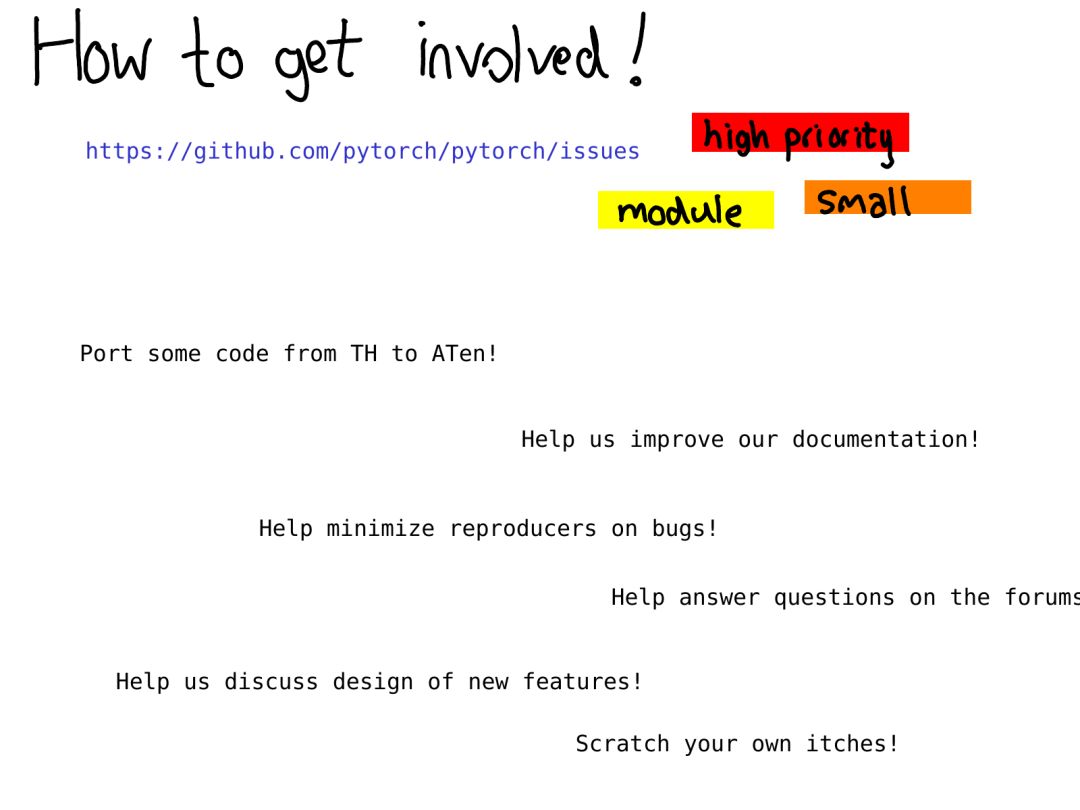
What’s next? What contributions can you make? Our issue tracker is a good place to start: https://github.com/pytorch/pytorch/issues.

Since this year, we have been categorizing and identifying issues; issues labeled as “triaged” indicate that at least one PyTorch developer has looked into it and made an initial assessment of the issue. You can use these labels to find out what issues we consider high priority or check out issues related to specific modules (like autograd) and also find issues we consider to be small problems. (Warning: we are sometimes wrong!)

Even if you don’t want to start writing code immediately, there are still many other useful works worth doing, such as improving documentation (I love merging documentation PRs; they are all great), helping us reproduce bug reports from other users, and helping us discuss RFCs on the issue tracker. Without our open-source contributors, PyTorch wouldn’t be where it is today; we hope you can join us.