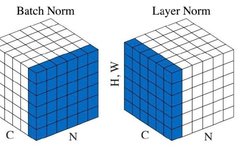
The comparison between Batch Norm and Layer Norm has become a common topic in the field of algorithms. The question of why BERT uses layer norm instead of batch norm has been asked countless times, and a simple search on Zhihu yields many explanations about the differences between BN and LN. Typically, people will provide this image:
▲ BN vs LN
People will say that for CV and NLP problems, the three dimensions here represent different information:

If we only look at the NLP problem, assuming our batch is (2,3,4), i.e., batch_size = 2, seq_length = 3, dim = 4, and assuming the first sentence is w1 w2 w3, and the second sentence is w4 w5 w6, then this tensor can be represented as:
[[w11, w12, w13, w14], [w21, w22, w23, w24], [w31, w32, w33, w34]
[w41, w42, w43, w44], [w51, w52, w53, w54], [w61, w62, w63, w64]]
We find that if it is BN, we would average the tokens at the corresponding positions in the same batch, meaning that (w11+w12+w13+w14+w41+w42+w43+w44)/8 is one of the means, resulting in a total of 3 means, which corresponds to C (seq_length) means in the image above.
However, if it is LN, it appears to calculate the mean of all features in each sample, i.e., (w11+w12+w13+w14+w21+w22+w23+w24+w31+w32+w33+w34)/12, resulting in a total of 2 means, which corresponds to N (batch_size) means in the image.
I have always believed in this calculation, thinking that BERT implements it this way, but one day I saw this answer from @猛猿 in this response: Why does Transformer use LayerNorm? [1] where the author provided two images:
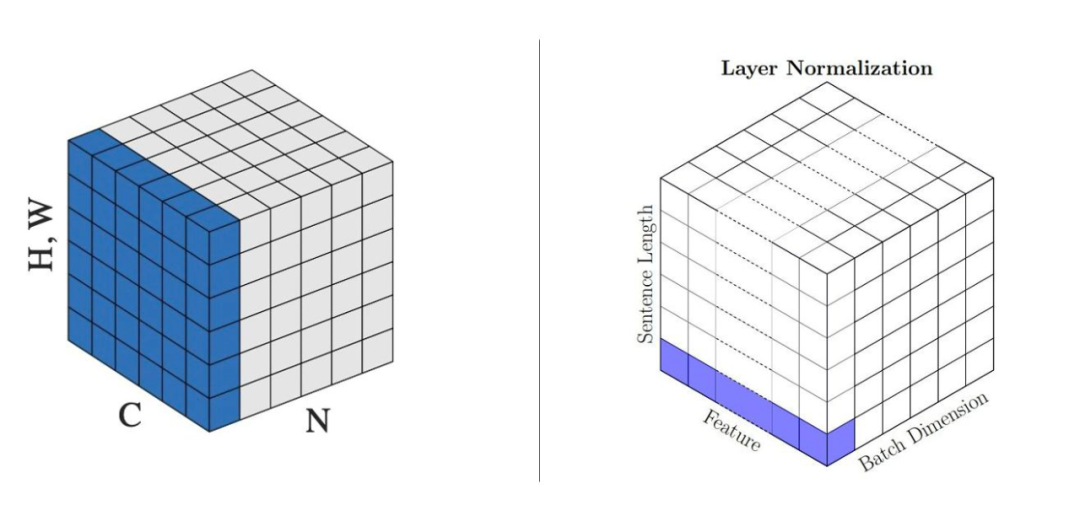
▲ Both are Layer Norm but different
The left image aligns with what I have always considered LN, but the right image averages over a single token, bringing us back to the original question: for a (2,3,4) tensor, (w11+w12+w13+w14)/4 is one mean, resulting in a total of 2*3=6 means.
So, in BERT, is it batch_size means (the calculation method of the left image), or batch_size*seq_length means (the calculation method of the right image)? We need to look at the source code.
The PyTorch source code for BERT or the transformer encoder is quite famous, including the built-in transformer encoder in torch and the implementation by Hugging Face. Let’s look at them one by one.
# torch.nn.TransformerEncoderLayer
# https://github.com/pytorch/pytorch/blob/master/torch/nn/modules/transformer.py
# Line 412
self.norm1 = LayerNorm(d_model, eps=layer_norm_eps, **factory_kwargs)
# huggingface bert_model
# https://github.com/huggingface/transformers/blob/3223d49354e41dfa44649a9829c7b09013ad096e/src/transformers/models/bert/modeling_bert.py#L378
# Line 382
self.LayerNorm = nn.LayerNorm(config.hidden_size, eps=config.layer_norm_eps)
It can be seen that whether in the built-in torch or the Hugging Face implementation of the transformer encoder or BERT layer, the nn.LayerNorm used is from torch itself, with parameters corresponding to the hidden dimension of 768 (the transformer calls it d_model, and BERT calls it hidden_size).
Now let’s see what nn.LayerNorm(dim) does. The following code is modified from Understanding torch.nn.LayerNorm in NLP [2]
import torch
batch_size, seq_size, dim = 2, 3, 4
embedding = torch.randn(batch_size, seq_size, dim)
layer_norm = torch.nn.LayerNorm(dim, elementwise_affine = False)
print("y: ", layer_norm(embedding))
eps: float = 0.00001
mean = torch.mean(embedding[:, :, :], dim=(-1), keepdim=True)
var = torch.square(embedding[:, :, :] - mean).mean(dim=(-1), keepdim=True)
print("mean: ", mean.shape)
print("y_custom: ", (embedding[:, :, :] - mean) / torch.sqrt(var + eps))
In the above code, I first generated an embedding and then calculated the result after applying nn.LayerNorm(dim). At the same time, I manually calculated the mean along the last dimension (which means my mean dimension is 2*3, resulting in a total of 6 means). If the results match, then nn.LayerNorm(dim) provides (batch_size*seq_length) means, which corresponds to the method on the right in the earlier image. The calculation results are as follows:
y: tensor([[[-0.2500, 1.0848, 0.6808, -1.5156],
[-1.1630, -0.7052, 1.3840, 0.4843],
[-1.3510, 0.4520, -0.4354, 1.3345]],
[[ 0.4372, -0.4610, 1.3527, -1.3290],
[ 0.2282, 1.3853, -0.2037, -1.4097],
[-0.9960, -0.6184, -0.0059, 1.6203]]])
mean: torch.Size([2, 3, 1])
y_custom: tensor([[[-0.2500, 1.0848, 0.6808, -1.5156],
[-1.1630, -0.7052, 1.3840, 0.4843],
[-1.3510, 0.4520, -0.4354, 1.3345]],
[[ 0.4372, -0.4610, 1.3527, -1.3290],
[ 0.2282, 1.3853, -0.2037, -1.4097],
[-0.9960, -0.6184, -0.0059, 1.6203]]])
They are indeed consistent, which means that at least in the built-in torch and the Hugging Face implementation of BERT, layer norm actually computes the mean for each token’s features separately.
So if we want to calculate batch_size means like in the left image, we just need to modify the parameters of nn.LayerNorm to nn.LayerNorm([seq_size,dim]). The code is as follows, and you can run it to find that it is consistent with calculating batch_size means:
import torch
batch_size, seq_size, dim = 2, 3, 4
embedding = torch.randn(batch_size, seq_size, dim)
layer_norm = torch.nn.LayerNorm([seq_size,dim], elementwise_affine = False)
print("y: ", layer_norm(embedding))
eps: float = 0.00001
mean = torch.mean(embedding[:, :, :], dim=(-2,-1), keepdim=True)
var = torch.square(embedding[:, :, :] - mean).mean(dim=(-2,-1), keepdim=True)
print("mean: ", mean.shape)
print("y_custom: ", (embedding[:, :, :] - mean) / torch.sqrt(var + eps))
The last question is, if we calculate as shown on the right, isn’t it the same as InstanceNorm? I also did a code experiment:
from torch.nn import InstanceNorm2d
instance_norm = InstanceNorm2d(3, affine=False)
x = torch.randn(2, 3, 4)
output = instance_norm(x.reshape(2,3,4,1)) # InstanceNorm2D requires input shape of (N,C,H,W)
print(output.reshape(2,3,4))
layer_norm = torch.nn.LayerNorm(4, elementwise_affine = False)
print(layer_norm(x))
You can run this and find that they are indeed consistent.
Conclusion: In BERT, the layer norm in both the built-in torch transformer encoder and the Hugging Face implementation actually performs InstanceNorm.
So, what was the original intention of using layer norm proposed by Vaswani in “Attention Is All You Need”? The author of tf.tensor2tensor is also Vaswani, so I believe that tf.tensor2tensor should align with the author’s initial source code design. After reviewing the source code (which involved looking through numerous files), I confirmed that the layer norm used by the author in their code also applies to the last dimension. Thus, the original author essentially used InstanceNorm.
Finally, I want to ask, is InstanceNorm a type of LayerNorm? Why haven’t I seen any related statements?
References
[1] https://www.zhihu.com/question/487766088/answer/2309239401

Scan the QR code to add the assistant on WeChat
About Us