Word2Vec Algorithm Derivation & Implementation

Word2Vec Algorithm Derivation & Implementation

by
Author: Guo Bi Yang

This article mainly summarizes the computational and programming problems from cs224n’s assignment 2. I found this assignment design to be excellent, progressing step by step, with both theory and practice, and a moderate level of difficulty. The overall structure feels more like a detailed tutorial. Therefore, I will review and reflect on Word2Vec based on these problems.
The main content of this article:
  • Word2Vec using Naive Softmax loss function
  • Word2Vec using Negative Sampling loss function
  • Details of the programming implementation

Some Notations

The goal of skip-gram is to learn the probability of predicting a specific word in its context given a center word. Here, ‘o’ means outside, and ‘c’ means center. Where do we find ‘o’? We need to first determine a window size, for example, in the figure below, using a window size of 2, the center word “banking” can find 4 context words:
Word2Vec Algorithm Derivation & Implementation

Word2Vec skip-gram algorithm with a window size of 2

Naive Softmax Loss Function

For this, we can construct the inner product of word vectors and then use the softmax function:
Here we have used two sets of word vector representations for the center word ‘c’ and the context word ‘o’, but note that the shapes of both are exactly the same, not complementary.
Thus, for a single word pair <c,o>, the loss function can be written as:
In fact, this loss function can also be represented as the cross-entropy between the true distribution of surrounding words and the predicted probability distribution, that is:

1. Prove that the negative log loss function of probability is equivalent to the cross-entropy loss function

This is the first question of assignment 2. The proof is quite simple: because the true distribution is a one-hot vector, meaning that only the position of the current true context word ‘o’ is 1. Thus,
which proves the statement.

2. Calculate the derivative of naive-softmax loss with respect to the center word and context word

For differentiation, there is no need for excessive explanation; it’s just the chain rule. Below is the differentiation process:
Differentiating with respect to the center word vector:
Differentiating with respect to the context word vector:
At this point, we need to consider cases; when w=o:
And when w!=o:
Both cases can be combined as:
From the above derivation results, we can see something: when we differentiate with respect to the center word, we only calculated the derivative for the center word at the current position ‘c’. Why? Because the derivatives at other positions are all 0! From the expression of J, it can be seen that J is independent of the center word vectors at positions other than ‘c’! However, when differentiating with respect to the context word, we find that regardless of whether the word is at the current position ‘o’, the derivative exists. Therefore, we need to calculate for all words in the vocabulary.
What does this tell us?
During parameter updates, updating the vector is easy, but updating the vectors is quite difficult.

Negative Sampling

In the process of deriving the naive softmax loss function above, we found that the computational overhead when updating U is significant. Therefore, we need to find a way to reduce such computational overhead. The negative sampling technique is currently the most practical method to reduce computation in Word2Vec.
Assuming the current center word is ‘c’, we select K negative sampling words from the vocabulary, denoted as ‘w’, with their corresponding word vectors. It is important to avoid the current true context word ‘o’, which is actually the positive sample. Thus, we can construct a new loss function—the negative sampling loss function:
This loss function is clearly easier to differentiate than the naive-softmax loss because it only updates K+1 vectors when updating the U matrix, while naive-softmax requires updating all vectors in U. In the negative sampling loss function, we no longer use the softmax activation function but instead use the sigmoid function. Thus, many people say that negative sampling transforms the original softmax |V| class classification into a few binary classification problems.
We will differentiate this loss function using the same method as in the previous section.
Before differentiating, we can first calculate the characteristics of the sigmoid function’s derivative to facilitate our differentiation:
Differentiating with respect to the center word vector:
Differentiating with respect to the context word vector:
Differentiating with respect to the context word vector:

Window Loss

The loss functions written above are for a single word pair <c,o>, while skip-gram uses a sliding window mechanism. Therefore, we need to further calculate the loss across an entire context window:
The J following the equation can be replaced with either naive-softmax loss or negative sampling loss, which will not be elaborated further here.

Programming Implementation of Word2Vec

This is the programming part of cs224n assignment 2.
Of course, we are not implementing the Word2Vec algorithm from scratch; that would be too complex. The assignment mainly involves filling in the blanks, allowing us to fill in the core parts of the algorithm. We do not need to worry about many system designs.
The main parts we need to write are these four: A. naive softmax loss and its derivative B. negative sampling loss and its derivative C. calculation of loss for one window D. parameter updates in the SGD optimization algorithm
These parts are based on the various derivatives we calculated above, and our derivative results are already in matrix operations, which is very convenient. The code I wrote has been uploaded to GitHub: https://github.com/beyondguo/CS224n-notes-and-codes/tree/master/assignment 2
I would like to record some programming tips separately:
  • Dimension issues in various matrix operations in numpy
  • How to use Vectorization to replace inefficient for training.

Python Multiplication, np.multiply() and np.dot()

One image illustrates:

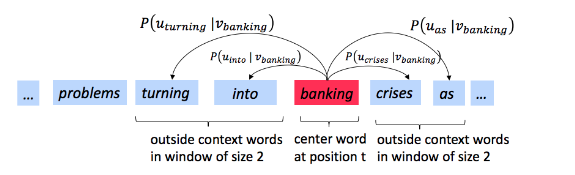
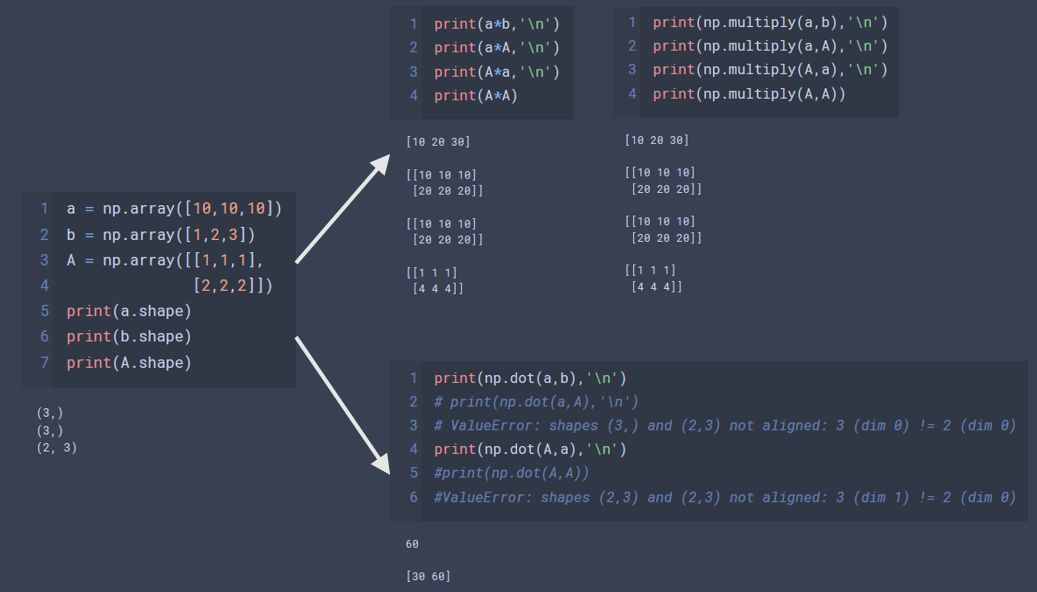
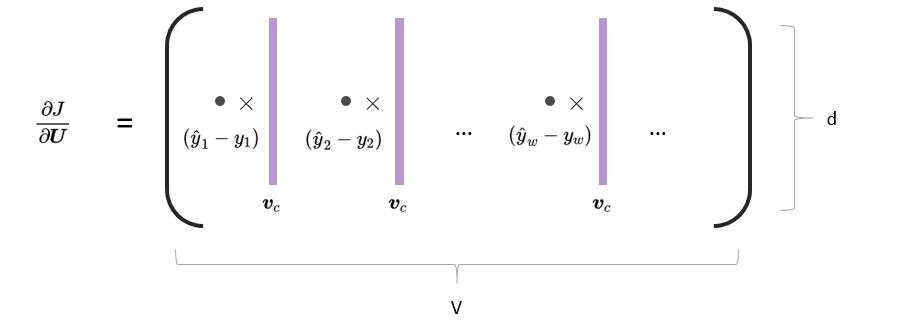
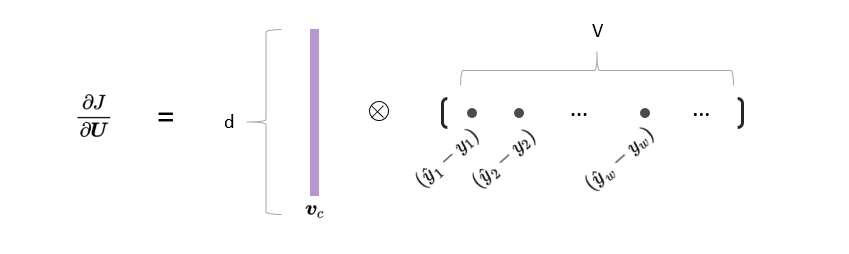
Word2Vec Algorithm Derivation & Implementation

In summary, np.multiply() and ordinary multiplication are equivalent; when shapes are the same, they perform “element-wise multiplication” while retaining the original shape. When shapes differ, the smaller matrix will utilize the “broadcasting mechanism” to multiply with the larger matrix.
np.dot, on the other hand, is legitimate matrix multiplication and must adhere to dimensional constraints; mismatched dimensions will result in an error. The only exception is when taking the dot product of two vectors, where no transposition is needed.

About Vectorization

All functions in np can operate on scalars, vectors, and matrices. Therefore, if you need to apply the same function to all elements in a matrix, you can directly pass the entire array to the np function. Additionally, when performing calculations, if the final target is a matrix, it is best to express it in matrix form during derivation to avoid unnecessary for loops.
For example, in the assignment, we need to find the derivative of J with respect to U. During differentiation, we have already calculated:
The derivative of J with respect to U is obtained by calculating the derivatives of each column of U and then assembling them. However, we can directly express this process in matrix form:
The following two images illustrate our transformation process:

Word2Vec Algorithm Derivation & ImplementationWord2Vec Algorithm Derivation & Implementation

Therefore, if following the for loop approach, the code would be to separately compute the derivative for each vector of U and then assemble it into a matrix:
gradU = np.array([v_c*(softmax(np.dot(U.T,v_c))[x]-int(x==o)) 
for x in range(U.shape[0])])
Whereas, if using the matrix representation we computed earlier, the code would be like this:
gradOutsideVecs = np.dot((y_hat-y).reshape(-1,1),v_c.reshape(1,-1))
# (V,),(d,)--&gt;(V,d)
The latter will be much more efficient.

Other Interesting and Useful Functions in Numpy

Here are two functions I find very useful:
  1. Directly extracting a series of specified indexed elements from an ndarray object through an array
a = np.array([0,10,20,30,40,50,60,70])
indices = np.array([0,2,4,6])
a[indices]
Output: array([ 0, 20, 40, 60])
A = np.array([[1,1,1],
              [2,2,2],
              [3,3,3]])
indices = np.array([0,2])
A[indices]
Output: array([[1, 1, 1],[3, 3, 3]])
Whether it is an array or a matrix, you can directly extract them. Note that the indices must be in np.array format.
  1. Using the at function to perform operations at specified positions
For example, if we have a large matrix and want to add a set of values to certain columns:
C = np.zeros((5,3))
temp = np.ones((2,3))
print('C:\n',C)
print('temp:\n',temp)
Let’s see what C and temp look like:
C:
 [[0. 0. 0.]
 [0. 0. 0.]
 [0. 0. 0.]
 [0. 0. 0.]
 [0. 0. 0.]]
temp:
 [[1. 1. 1.]
 [1. 1. 1.]]
Next, we want to add the values of the two vectors in temp to rows 0 and 2 of C, we can simply write:
np.add.at(C,[0,2],temp)
C
Output:
array([[1., 1., 1.],
       [0., 0., 0.],
       [1., 1., 1.],
       [0., 0., 0.],
       [0., 0., 0.]])
Look! It’s that convenient! Here, add can be replaced with various other operations.
That’s all.
Recommended Reading

2021 iFLYTEK - Vehicle Loan Default Prediction Competition Top 1 Solution (Python Code)
10 Complete Python Operations for Clustering Algorithms
Why Use MSE for Regression Problems?
Stability Analysis of Time Series Feature Correlation Coefficients (with Code)
Summary of Time Series Prediction Methods: From Theory to Practice (with Kaggle Classic Competition Solutions)

Leave a Comment