Discussion on Absolute, Relative, and Rotational Position Encoding in Transformers

Reprinted from Zhihu: Yao Yuan Link: https://zhuanlan.zhihu.com/p/17311602488

1. Introduction

The attention mechanism in Transformer [1] can effectively model the correlations between tokens, achieving significant performance improvements in many tasks. However, the attention mechanism itself does not have the capability to perceive token positional information, meaning that the results after the attention mechanism calculation depend solely on the correlation between tokens and are unrelated to the positional information of the tokens. As is well known, positional information is crucial in long sequence modeling, so a mechanism is needed to explicitly encode the positional information of each token, allowing the model to perceive the position of each token. Currently, position encoding can be roughly divided into three categories: absolute position encoding, relative position encoding, and fused position encoding. This article summarizes several common position encodings based on some high-quality blogs [2-4] and my own understanding for reference.

All experimental code mentioned below can be found at: Learn_PositionEncoding_Colab

2. The Role of Position Encoding

Before formally introducing position encoding, let’s review the attention mechanism in Transformer. Suppose we denote the query vector and key vector of two tokens at positions and as follows, the calculation formula for the attention weight is:

If it is not a function of position and not a function of position, then regardless of how the distance between the two tokens in the sequence changes, their attention weights will not change. This contradicts human intuition, as typically, the closer two tokens are, the greater their attention weight should be. To solve this problem, positional information is explicitly introduced into each word vector, allowing each token to perceive its position in the input sequence. Specifically, we define a function that encodes positional information into the word vector through a function. After incorporating positional information, the calculation formula for the attention weight is as follows:

At this point, once the positional information of two tokens changes, their attention weights will also change accordingly.

3. Absolute Position Encoding

Absolute position encoding assigns a specific encoding to each position, uniquely identifying the position of each token in the sequence. Common methods of absolute position encoding include learnable position encoding and sinusoidal position encoding.

3.1 Learnable Positional Encoding

Learnable positional encoding is an intuitive and straightforward absolute position encoding method, where the encoding is learned by the model during training. Specifically, suppose the dimensionality of the word vector is 256, and the length of the input token sequence is 512, a position encoding matrix can be randomly initialized, where the row vector represents the position encoding corresponding to the position. During the training process of the model, this matrix will be gradually updated to learn the optimal position encoding matrix. In the inference phase, the final trained matrix will be used to provide corresponding position encodings for each position.

Learnable position encoding has the following characteristics:

• High Flexibility: Since the above position encoding matrix is learned from data during the model’s training process, it has high flexibility. Theoretically, learnable position encoding can be applied to different types of tasks or sequence lengths.
• Limited Range: Learnable position encoding has limitations regarding sequence length, lacking extrapolation capability. If the length of the token sequence input during the inference phase exceeds the maximum token sequence length during the training phase, the model may not effectively handle these out-of-range tokens due to the lack of corresponding position encoding vectors, thereby affecting inference performance.

3.2 Trigonometric Positional Encoding

This is the position encoding method used in the Transformer paper [1]. I personally find it a fascinating encoding method and really admire the creativity of Google’s researchers. Specifically, for position , the sine position encoding’s -th component is calculated as follows:

According to the above formula, each dimension of the trigonometric position encoding is actually a sine function (for even dimensions) or a cosine function (for odd dimensions) of the position, using sine and cosine functions based on the parity of the dimension. The purpose of this design is not explicitly explained in the original Transformer paper [1]. I personally feel that this design allows the model to distinguish the parity of dimensions, enhancing the model’s expressiveness (I feel that some interpretations of the sine and cosine design might be overinterpretations, and I welcome everyone to share their views). Trigonometric position encoding mainly has the following advantages:

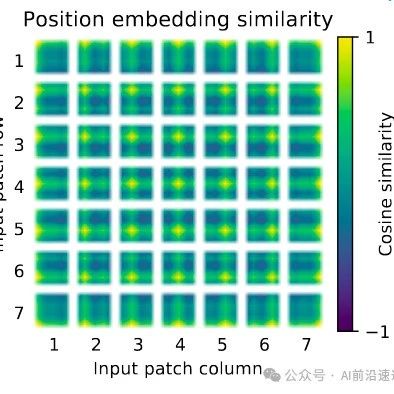
1. Trigonometric functions are periodic, which makes each dimension’s component periodic, thereby allowing for natural extrapolation. As shown in the figure below, each dimension’s component is a trigonometric function, and by inputting different positions, the corresponding encoding values can be calculated. Even during the inference phase, if the sequence length exceeds the maximum length used during training, the corresponding encoding values can still be calculated directly based on the trigonometric function of that dimension.

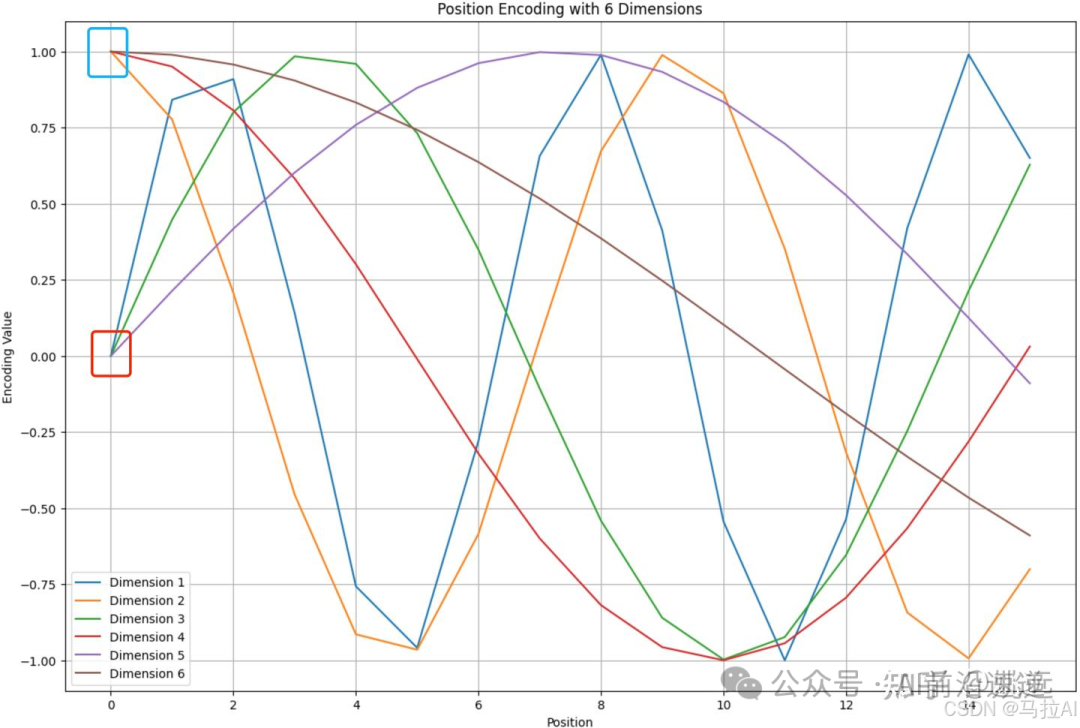
2. Trigonometric position encoding itself has the property of remote attenuation, meaning that for two different position encoding vectors, when they are close together, their inner product is large; conversely, as the distance between them increases, the inner product value decreases and exhibits an oscillating attenuation trend. As shown in the figure below, and are two different position encoding vectors, and as their distance increases, their inner product gradually oscillates and attenuates. 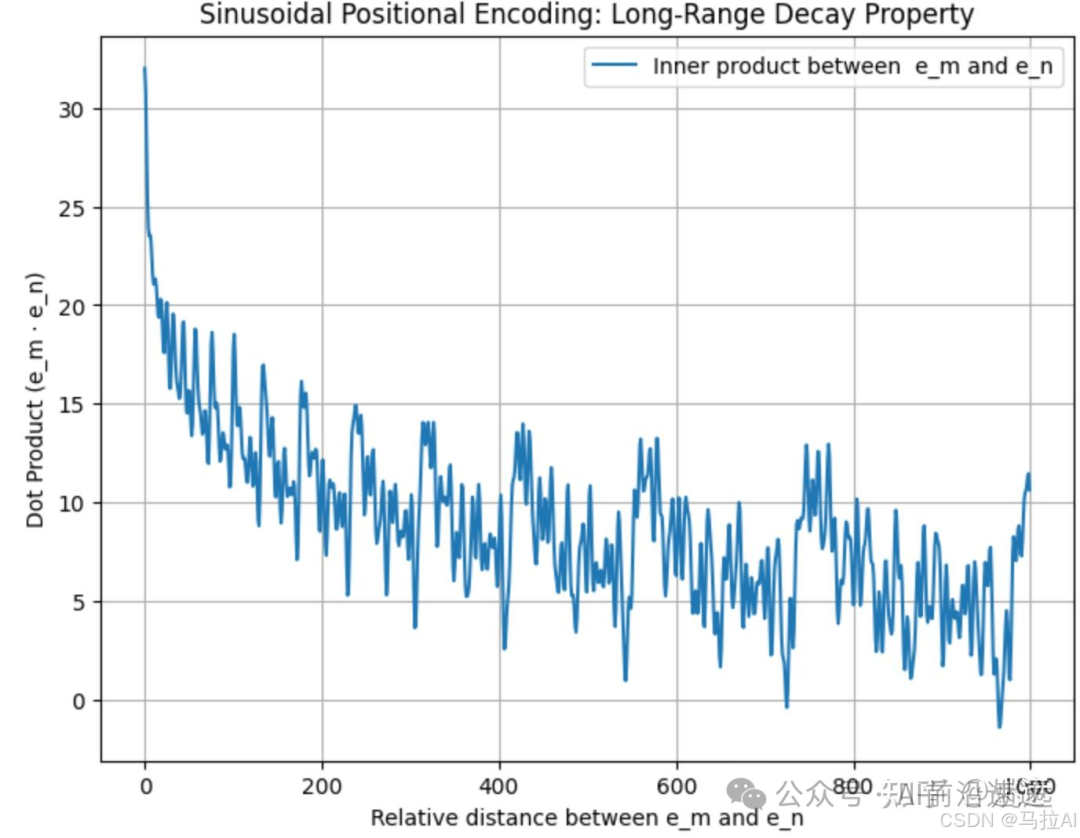Note that the trigonometric position encoding has the property of remote attenuation. I tested that if position encoding is directly added to the word vectors, i.e., and two different word vectors, it does not effectively reflect the remote attenuation property, as shown in the figure below. 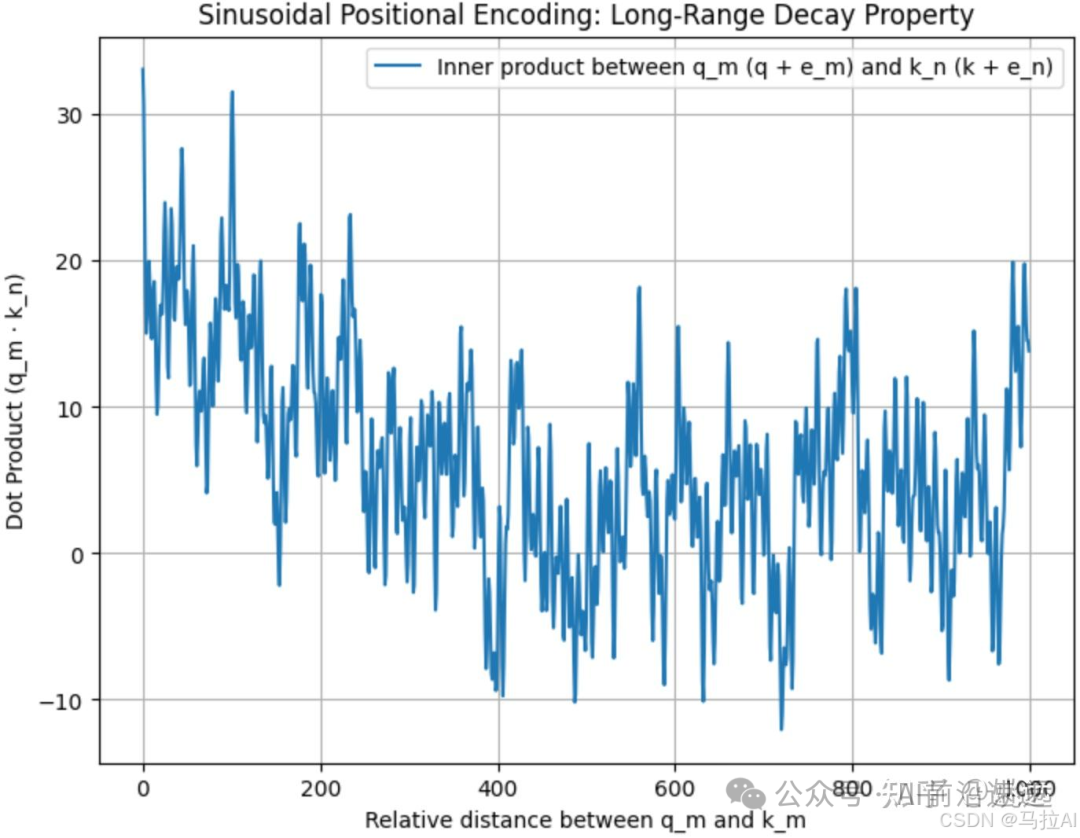However, if the position encoding is concatenated with the word vectors (all vectors are column vectors), i.e., and are concatenated, it still retains the remote attenuation property, as shown in the figure below.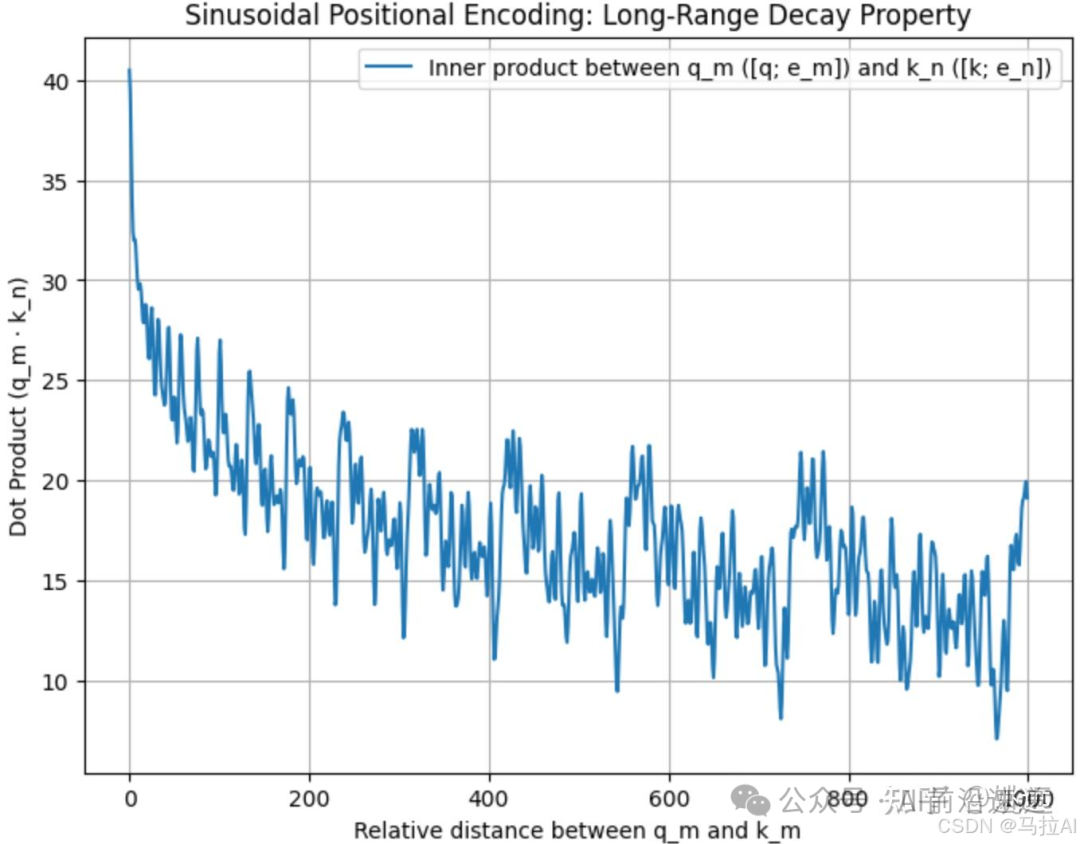

So, based on the above two sets of experiments, would concatenating position encoding be a better approach?

1. Trigonometric functions have the following properties:

The above formula indicates that the position encoding vector can be obtained by combining the position and position encoding vectors. This is a good property that indicates that using trigonometric functions for position encoding can express relative positions to a certain extent, allowing the model to understand the relationship of “adjacent positions”.

4. Relative Position Encoding

Relative position encoding focuses on the positional relationship between a word and other words, rather than absolute positions. This method is more suitable for tasks where the relative order in the sequence is more important than absolute positions (e.g., sentence understanding). Google’s researchers proposed using relative position encoding in Transformer in 2018 [5], with the specific calculation method as follows:

Where and denote the learnable relative position vectors for positions and , and and denote the query, key, and value word vectors respectively.

5. Fused Position Encoding

Fused position encoding is a method that combines the advantages of both absolute and relative position encodings. One of the most representative encoding methods is the Rotational Position Encoding [6], which, through rigorous mathematical derivation, designs a very elegant position encoding mechanism that can embed absolute positional information into word vectors while also reflecting relative positional information after the attention mechanism calculation. Since the calculation of attention weights essentially involves computing the inner product of vectors, rotational position encoding aims to solve the following mathematical problem: to find a function and a function such that to solve the above problem, rotational position encoding approaches it from a complex number perspective, deriving a set of functions and a function that satisfy the above conditions (for specific derivation processes, please refer to [2,3]). Specifically, for two-dimensional word vectors, let

then the following formula holds: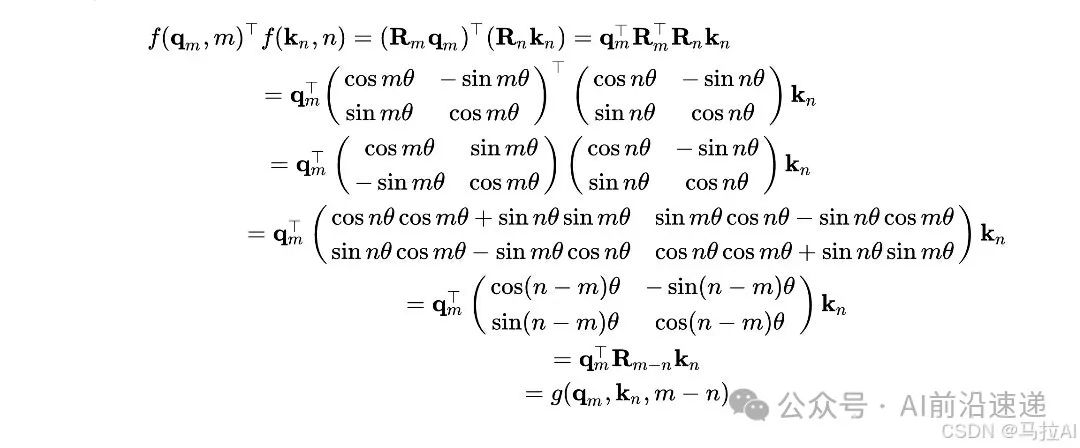

Accordingly, when , where is a common rotation matrix in geometry. The function serves to rotate the word vector at a specific angle, thereby only changing the direction of the word vector without altering its length. This means that by performing a rotation operation on the vector, positional information can be encoded into the word vector. In other words, under the setting of rotational position encoding, the positional information of each word vector can be understood as the angle that each word vector needs to rotate. Therefore, this position encoding is also referred to as rotational position encoding. The above formula derives the basic principle of rotational position encoding from the perspective of two-dimensional word vectors. Since rotation matrices have orthogonality, for high-dimensional data (usually the dimensionality of word vectors is even), positional encoding can be achieved by grouping the dimensions of the word vectors in pairs and rotating each group separately. The specific calculation process is as follows:

In addition, rotational position encoding borrows the design concept of trigonometric position encoding, setting different constants for each group to achieve the effect of distance attenuation, thereby better capturing the relationships between different positions in the sequence:

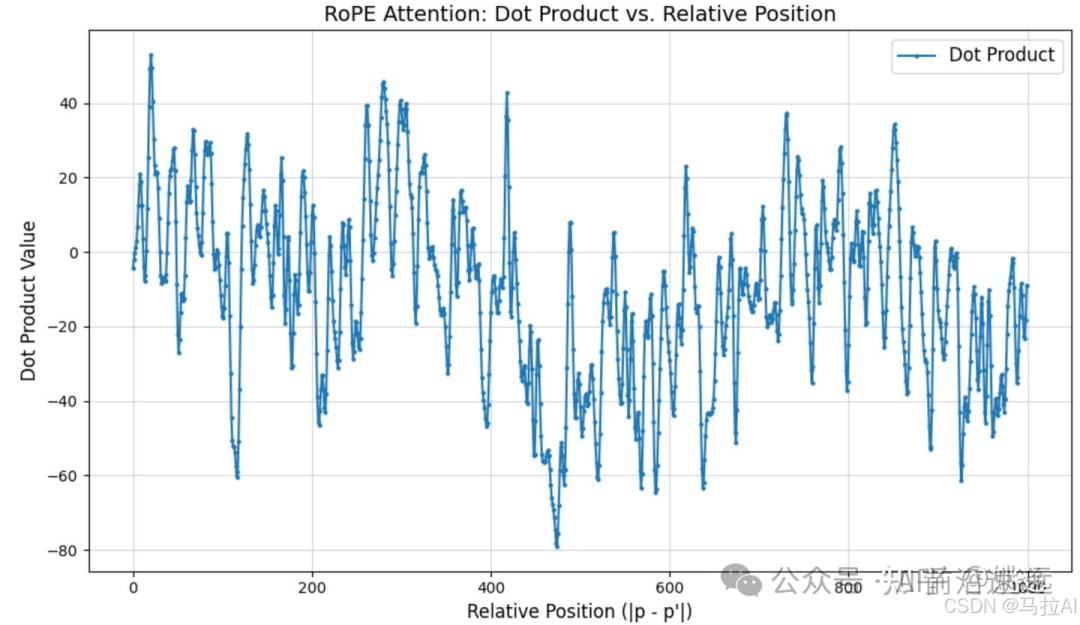
I tested the remote attenuation property of rotational position encoding, but did not achieve very satisfactory results; the specific reason is unclear (not sure if there is an issue with the testing code).

6. Conclusion

The emergence of position encoding is primarily to address the defect of the attention mechanism in Transformer that cannot model positional information. Various position encodings have been proposed, including absolute position encoding, relative position encoding, and fused position encoding that combines the strengths of all. Since most of the current large models are based on the Transformer architecture, research on position encoding is crucial. First of all, I truly admire Google’s researchers for thinking of using the properties of trigonometric functions to model position encoding, which has sparked many subsequent studies. In addition, I feel that my understanding of position encoding is still not very profound, and I have some questions: Is it reasonable to assume that position encoding has periodicity? Why does position encoding need to be periodic? Are there more suitable functions to model position encoding? I believe that more elegant position encodings will emerge in this field in the future.