Machine Heart Reports
Editor: Zhao Yang
Recently, a paper was published on arXiv, providing a new interpretation of the mathematical principles behind Transformers. The content is extensive and rich in knowledge, and I highly recommend reading the original.
In 2017, Vaswani et al. published “Attention Is All You Need,” marking a significant milestone in the development of neural network architectures. The core contribution of this paper is the self-attention mechanism, which is the innovation that distinguishes Transformers from traditional architectures and plays a crucial role in their outstanding practical performance.
In fact, this innovation has become a key catalyst for advancements in artificial intelligence in fields such as computer vision and natural language processing, and it has also played a critical role in the emergence of large language models. Therefore, understanding Transformers, especially the mechanism of self-attention in processing data, is a vital but largely under-researched area.

Paper link: https://arxiv.org/pdf/2312.10794.pdf
Deep Neural Networks (DNNs) share a common feature: input data is processed sequentially, layer by layer, forming a time-discrete dynamic system (details can be referenced in the MIT-published “Deep Learning,” also known as the “Flower Book” in China). This perspective has been successfully used to model residual networks as time-continuous dynamic systems, known as neural ordinary differential equations (neural ODEs). In neural ODEs, input images 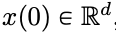 evolve over the time interval (0, T) according to a given time-varying velocity field
evolve over the time interval (0, T) according to a given time-varying velocity field  . Therefore, DNNs can be viewed as a flow mapping from one
. Therefore, DNNs can be viewed as a flow mapping from one 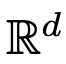 to another
to another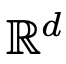 flow map
flow map 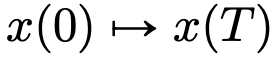 . Even under the constraints of classical DNN architectures, the velocity fields
. Even under the constraints of classical DNN architectures, the velocity fields 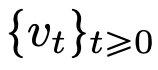 exhibit strong similarities between flow mappings.
Researchers have found that Transformers are actually mappings on
exhibit strong similarities between flow mappings.
Researchers have found that Transformers are actually mappings on 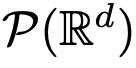 , specifically the mapping between d-dimensional probability measure spaces (the space of probability measures). To achieve this flow mapping between metric spaces, Transformers require the establishment of a mean-field interacting particle system.
Specifically, each particle (which can be understood as a token in the context of deep learning) follows the flow of a vector field, which depends on the empirical measure of all particles. In turn, the equations determine the evolution process of the particle empirical measures, which may take a long time and require continuous attention.
The researchers’ main observation is that the particles tend to eventually cluster together. This phenomenon is particularly evident in learning tasks such as unidirectional inference (i.e., predicting the next word in a sequence). The output measure encodes the probability distribution for the next token, and based on the clustering results, a small number of possible outcomes can be filtered.
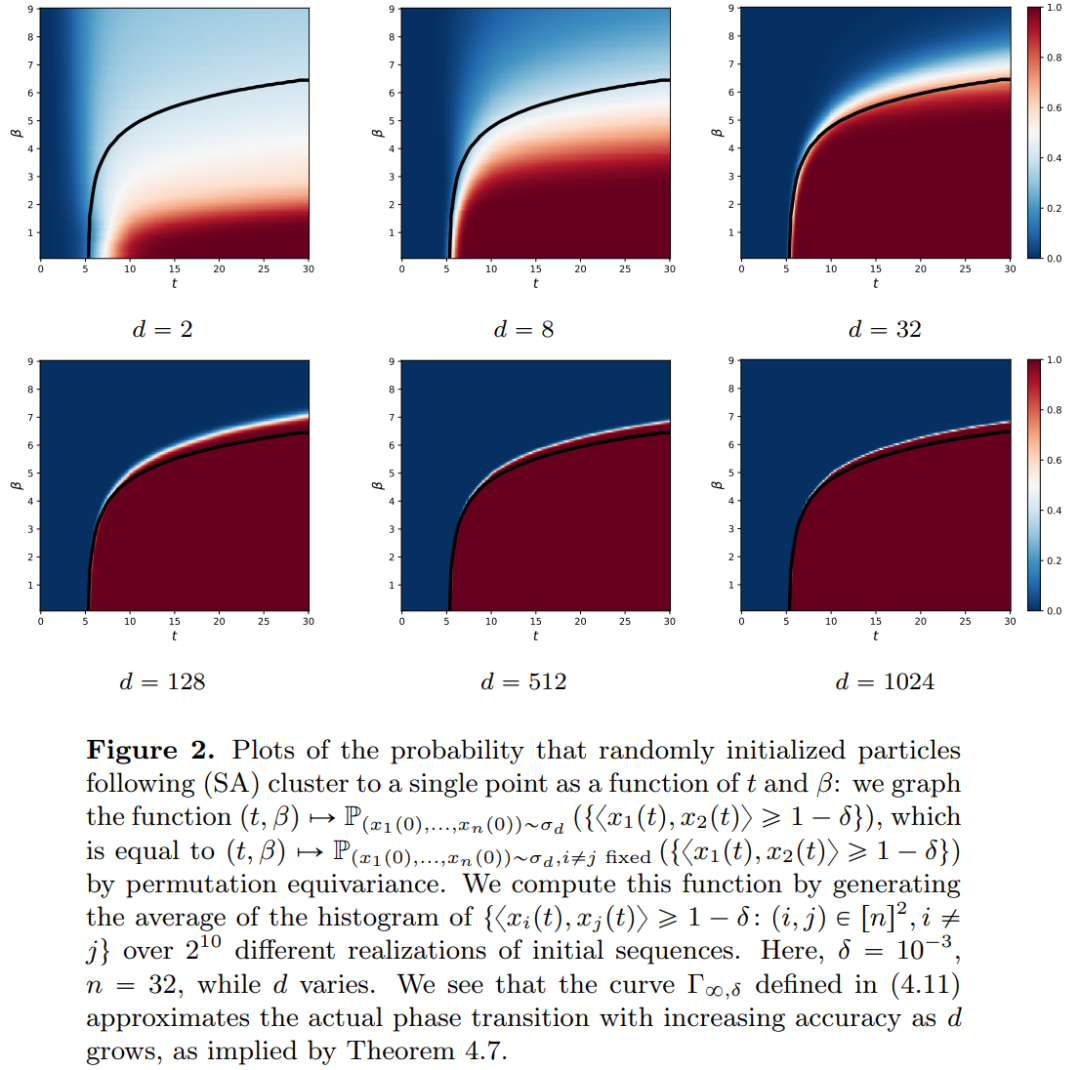
The research findings indicate that the limiting distribution is actually a point mass, with no diversity or randomness, which contradicts actual observations. This apparent paradox is resolved by the variable states of particles persisting over time. As shown in Figures 2 and 4, Transformers exhibit two different time scales: in the first phase, all tokens quickly form several clusters, while in the second phase (which is much slower than the first), through a pairwise merging process of the clusters, all tokens eventually collapse into a single point.
, specifically the mapping between d-dimensional probability measure spaces (the space of probability measures). To achieve this flow mapping between metric spaces, Transformers require the establishment of a mean-field interacting particle system.
Specifically, each particle (which can be understood as a token in the context of deep learning) follows the flow of a vector field, which depends on the empirical measure of all particles. In turn, the equations determine the evolution process of the particle empirical measures, which may take a long time and require continuous attention.
The researchers’ main observation is that the particles tend to eventually cluster together. This phenomenon is particularly evident in learning tasks such as unidirectional inference (i.e., predicting the next word in a sequence). The output measure encodes the probability distribution for the next token, and based on the clustering results, a small number of possible outcomes can be filtered.
The research findings indicate that the limiting distribution is actually a point mass, with no diversity or randomness, which contradicts actual observations. This apparent paradox is resolved by the variable states of particles persisting over time. As shown in Figures 2 and 4, Transformers exhibit two different time scales: in the first phase, all tokens quickly form several clusters, while in the second phase (which is much slower than the first), through a pairwise merging process of the clusters, all tokens eventually collapse into a single point.
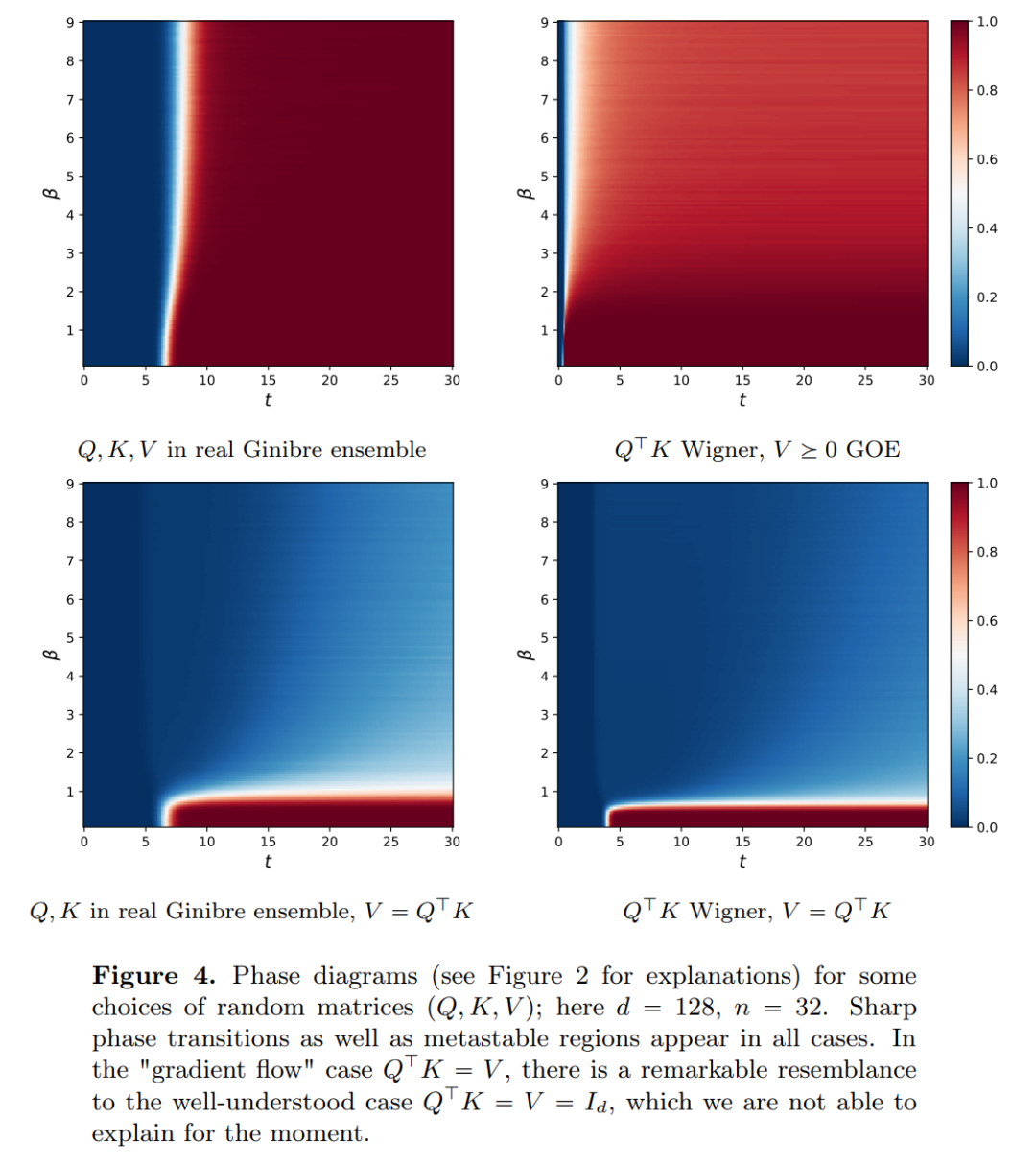
The goals of this paper are twofold. On one hand, the paper aims to provide a general and comprehensible framework for studying Transformers from a mathematical perspective. In particular, through the structure of these interacting particle systems, researchers can establish concrete connections with established themes in mathematics, including nonlinear transport equations, Wasserstein gradient flows, collective behavior models, and optimal configurations of points on spheres. On the other hand, the paper describes several promising research directions, with a special focus on clustering phenomena over long time spans. The primary result indicators proposed by the researchers are all new, and they also present interesting open questions throughout the paper.
The main contributions of this paper are divided into three parts.

Part 1: Modeling. This paper defines an ideal model of the Transformer architecture, treating the number of layers as a continuous time variable. This abstract approach is not novel and is similar to the methods used in classical architectures like ResNets. The model in this paper focuses only on two key components of the Transformer architecture: the self-attention mechanism and layer normalization. Layer normalization effectively confines particles within the unit sphere 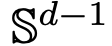 , while the self-attention mechanism achieves nonlinear coupling between particles through empirical measures. In turn, the empirical measures evolve according to continuity partial differential equations. The paper also introduces a simpler alternative model for self-attention, a Wasserstein gradient flow of an energy function, for which there are established methods for optimal configurations of points on spheres.
Part 2: Clustering. In this part, the researchers present new mathematical results regarding token clustering over longer time spans. For example, Theorem 4.1 indicates that a set of n particles randomly initialized on the unit sphere in high-dimensional space will cluster into a single point over time. The researchers provide a precise description of the contraction rate of the particle clusters to supplement this result. Specifically, they plot histograms of distances between all particles, as well as the time points when all particles are about to complete clustering (see Section 4 of the original paper). The researchers also obtained clustering results without assuming a large dimension d (see Section 5 of the original paper).
Part 3: Future Outlook. This paper primarily poses questions in the form of open problems and corroborates them with numerical observations, thereby suggesting potential routes for future research. The researchers first focus on the case where the dimension d = 2 (see Section 6 of the original paper), drawing connections to Kuramoto oscillators. They then briefly demonstrate how simple and natural modifications to the model can resolve optimization problems related to spheres (see Section 7 of the original paper). The following sections explore interacting particle systems, which could facilitate adjustments to parameters in the Transformer architecture and may lead to practical applications in the future.
, while the self-attention mechanism achieves nonlinear coupling between particles through empirical measures. In turn, the empirical measures evolve according to continuity partial differential equations. The paper also introduces a simpler alternative model for self-attention, a Wasserstein gradient flow of an energy function, for which there are established methods for optimal configurations of points on spheres.
Part 2: Clustering. In this part, the researchers present new mathematical results regarding token clustering over longer time spans. For example, Theorem 4.1 indicates that a set of n particles randomly initialized on the unit sphere in high-dimensional space will cluster into a single point over time. The researchers provide a precise description of the contraction rate of the particle clusters to supplement this result. Specifically, they plot histograms of distances between all particles, as well as the time points when all particles are about to complete clustering (see Section 4 of the original paper). The researchers also obtained clustering results without assuming a large dimension d (see Section 5 of the original paper).
Part 3: Future Outlook. This paper primarily poses questions in the form of open problems and corroborates them with numerical observations, thereby suggesting potential routes for future research. The researchers first focus on the case where the dimension d = 2 (see Section 6 of the original paper), drawing connections to Kuramoto oscillators. They then briefly demonstrate how simple and natural modifications to the model can resolve optimization problems related to spheres (see Section 7 of the original paper). The following sections explore interacting particle systems, which could facilitate adjustments to parameters in the Transformer architecture and may lead to practical applications in the future.
© THE END
For reprints, please contact this public account for authorization
Submissions or inquiries: [email protected]

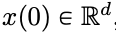 evolve over the time interval (0, T) according to a given time-varying velocity field
evolve over the time interval (0, T) according to a given time-varying velocity field  . Therefore, DNNs can be viewed as a flow mapping from one
. Therefore, DNNs can be viewed as a flow mapping from one 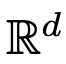 to another
to another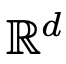 flow map
flow map  . Even under the constraints of classical DNN architectures, the velocity fields
. Even under the constraints of classical DNN architectures, the velocity fields 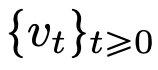 exhibit strong similarities between flow mappings.
exhibit strong similarities between flow mappings.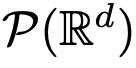 , specifically the mapping between d-dimensional probability measure spaces (the space of probability measures). To achieve this flow mapping between metric spaces, Transformers require the establishment of a mean-field interacting particle system.
, specifically the mapping between d-dimensional probability measure spaces (the space of probability measures). To achieve this flow mapping between metric spaces, Transformers require the establishment of a mean-field interacting particle system.


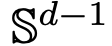 , while the self-attention mechanism achieves nonlinear coupling between particles through empirical measures. In turn, the empirical measures evolve according to continuity partial differential equations. The paper also introduces a simpler alternative model for self-attention, a Wasserstein gradient flow of an energy function, for which there are established methods for optimal configurations of points on spheres.
, while the self-attention mechanism achieves nonlinear coupling between particles through empirical measures. In turn, the empirical measures evolve according to continuity partial differential equations. The paper also introduces a simpler alternative model for self-attention, a Wasserstein gradient flow of an energy function, for which there are established methods for optimal configurations of points on spheres.