Machine Heart reports
Editors: Danjiang, Xiaozhou
SVM is all you need; Support Vector Machines are never out of date.
The Transformer is a new theoretical model of Support Vector Machines (SVM) that has sparked discussion in academia.
Last weekend, a paper from the University of Pennsylvania and the University of California, Riverside, sought to explore the principles behind the foundational Transformer structure of large models, establishing a formal equivalence between the optimization geometry of the attention layer and the hard boundary SVM problem separating optimal input tokens from non-optimal tokens.
On Hacker News, the author stated that this theory addresses the SVM’s challenge of separating “good” markers from “bad” tokens in each input sequence. This SVM acts as an efficient token selector, fundamentally different from traditional SVMs that assign 0-1 labels to inputs.
This theory also explains how attention induces sparsity through softmax: “bad” tokens that fall on the wrong side of the SVM decision boundary are suppressed by the softmax function, while “good” tokens are those that ultimately have non-zero softmax probabilities. It is also worth mentioning that this SVM originates from the exponential nature of softmax.
After the paper was uploaded to arXiv, many people expressed their opinions, with some saying: The direction of AI research is truly spiraling upward; are we going to circle back again?
After going around, Support Vector Machines are still not out of date.
Since the classic paper “Attention is All You Need” was published, the Transformer architecture has brought revolutionary advances to the field of Natural Language Processing (NLP). The attention layer in Transformers accepts a series of input tokens X and evaluates the correlation between tokens by calculating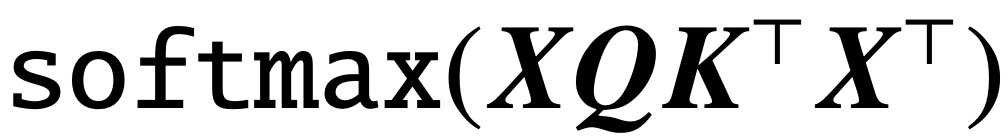 
where (K, Q) are trainable key-query parameters, effectively capturing long-range dependencies.
Now, a new paper titled “Transformers as Support Vector Machines” establishes a formal equivalence between the optimization geometry of self-attention and the hard-margin SVM problem, using the outer product linear constraints of token pairs to separate optimal input tokens from non-optimal tokens.
Paper link: https://arxiv.org/pdf/2308.16898.pdf
This formal equivalence is based on the paper by Davoud Ataee Tarzanagh et al., “Max-Margin Token Selection in Attention Mechanism,” which describes the implicit bias of a 1-layer transformer optimized through gradient descent:
(1) Optimizing the attention layer parameterized by (K, Q) converges to an SVM solution through vanishing regularization, where the nuclear norm of the combined parameters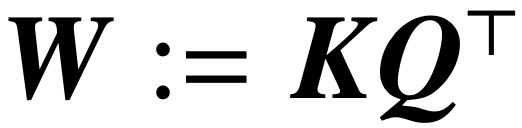 
is minimized. In contrast, direct parameterization through W minimizes the Frobenius norm SVM objective. The paper describes this convergence and emphasizes that it can occur in local optimal directions rather than global optimal directions.
(2) The paper also proves that the local/global directional convergence of gradient descent with W parameterization occurs under appropriate geometric conditions. Importantly, over-parameterization catalyzes global convergence by ensuring the feasibility of the SVM problem and guaranteeing a benign optimization environment without stationary points.
(3) Although the theory in this study primarily applies to linear prediction heads, the research team proposed a more general SVM equivalent that can predict the implicit bias of a 1-layer transformer with non-linear heads/MLPs.
Overall, the results of this study are applicable to general datasets, can be extended to cross-attention layers, and the practical validity of the research conclusions has been verified through thorough numerical experiments. This study establishes a new research perspective, viewing multi-layer transformers as a hierarchical structure for separating and selecting the best tokens.
Specifically, given an input sequence of length T and embedding dimension d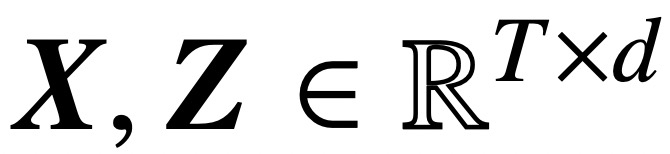 
, this study analyzes core cross-attention and self-attention models:
where K, Q, V are trainable key, query, and value matrices,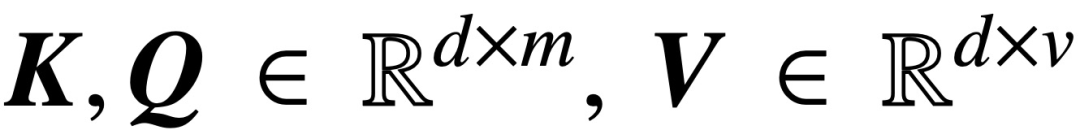 
; S (・) denotes the softmax non-linearity, which is applied row-wise to 
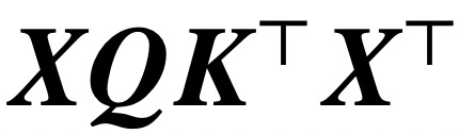. This study assumes that the first token of Z (denoted as z) is used for prediction. Specifically, given a training dataset 
, 
, 
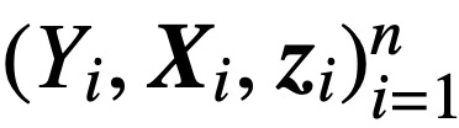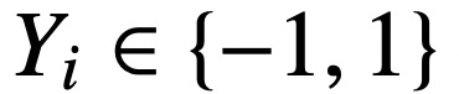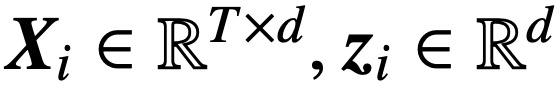, this study uses a decreasing loss function 
for minimization:
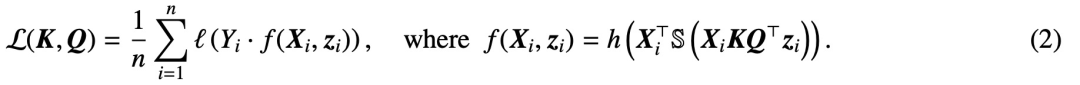
Here, h (・):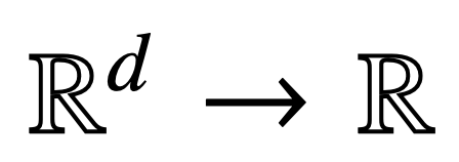 
is the prediction head containing value weights V. In this formulation, the model f (・) precisely represents a single-layer transformer, where an MLP follows the attention layer. The authors recover self-attention in (2) by setting 
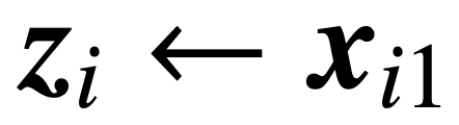where x_i denotes the first token of the sequence X_i. Due to the non-linear nature of the softmax operation, it poses significant challenges for optimization. Even if the prediction head is fixed and linear, the problem remains non-convex and non-linear. In this study, the authors focus on optimizing the attention weights (K, Q, or W) and overcoming these challenges, thereby establishing the fundamental equivalence of SVM.
The structure of the paper is as follows: Chapter 2 introduces the preliminary knowledge of self-attention and optimization; Chapter 3 analyzes the optimization geometry of self-attention, showing that the attention parameters RP converge to the maximum margin solution; Chapters 4 and 5 discuss global and local gradient descent analyses, respectively, showing that key-query variable W converges to the solution of (Att-SVM); Chapter 6 presents results regarding non-linear prediction heads and generalized SVM equivalence; Chapter 7 extends the theory to sequential prediction and causal prediction; Chapter 8 discusses related literature. Finally, Chapter 9 summarizes and proposes open questions and future research directions.
The main content of the paper is as follows:
Implicit Bias of the Attention Layer (Chapters 2-3)
Optimizing the attention parameters (K, Q) under the condition of vanishing regularization will converge directionally to the maximum margin solution 
, where the nuclear norm target is the combined parameters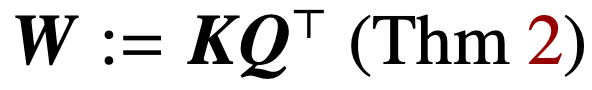 
. In the case of directly parameterizing cross-attention with combined parameters W, the regularization path (RP) converges directionally to the (Att-SVM) solution with the Frobenius norm as the target.
This is the first formal distinction between W and the optimization dynamics of (K, Q) parameters, revealing the latter’s low-order bias. The theory of this study clearly describes the optimality of the selected tokens and naturally extends to sequence-to-sequence or causal classification settings.
Convergence of Gradient Descent (Chapters 4-5)
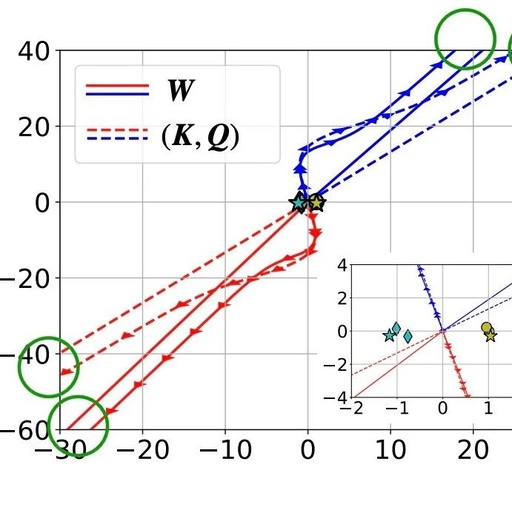
With appropriate initialization and linear head h (・), the gradient descent (GD) iterations of the combined key-query variable W converge directionally to the local optimal solution of (Att-SVM) (Section 5). To achieve local optimality, the selected tokens must score higher than adjacent tokens.
The local optimal direction is not necessarily unique and can be determined by the geometric characteristics of the problem [TLZO23]. As an important contribution, the authors identify the geometric conditions that ensure convergence to the global optimal direction (Chapter 4). These conditions include:
-
The best tokens have a significant score difference;
-
The initial gradient direction aligns with the best tokens.
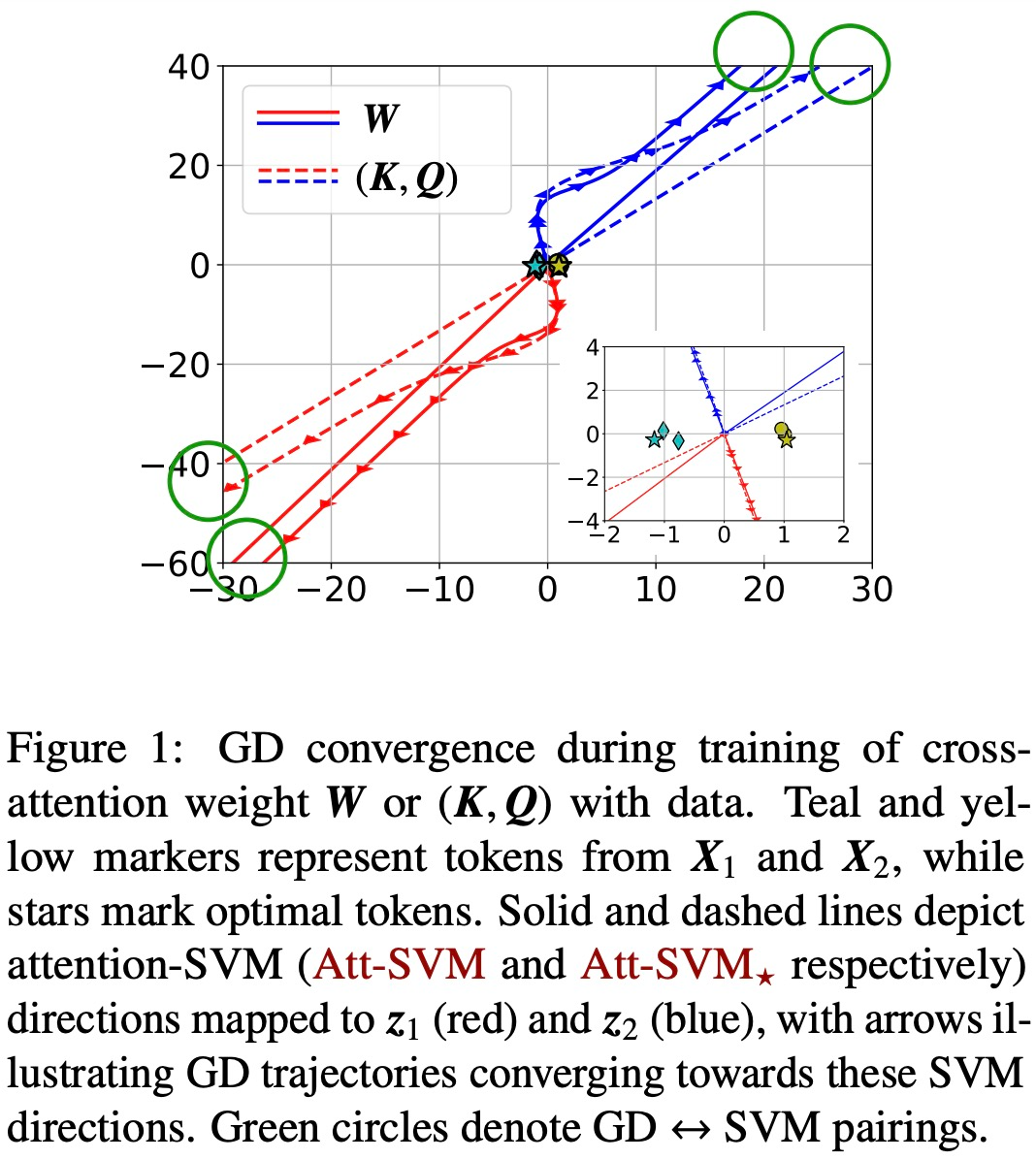
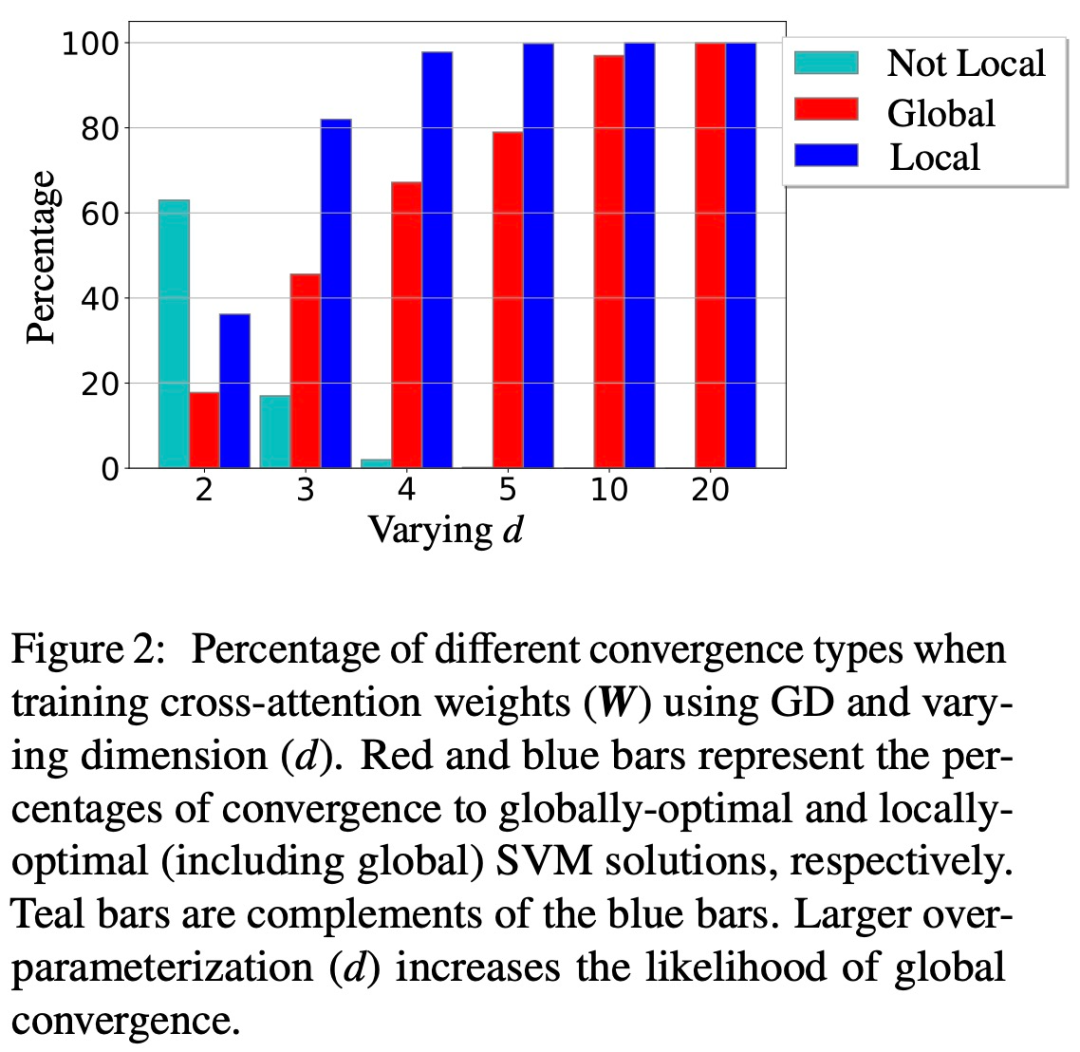
Additionally, the paper demonstrates that over-parameterization (i.e., a large dimension d, and equivalent conditions) catalyzes global convergence by ensuring (1) the feasibility of (Att-SVM), and (2) a benign optimization landscape (i.e., no stationary points and false local optimal directions) (see Section 5.2).
Figures 1 and 2 illustrate this.
Generality of SVM Equivalence (Chapter 6)
When optimizing with linear h (・), the attention layer inherently favors selecting one token from each sequence (also known as hard attention). This is reflected in (Att-SVM), manifested as the output token being a convex combination of input tokens. In contrast, the authors show that non-linear heads must consist of multiple tokens, highlighting their importance in the dynamic process of transformers (Section 6.1). Leveraging insights gained from the theory, the authors propose a more general SVM equivalence method.
Notably, they demonstrate that in universally unaddressed scenarios (e.g., h (・) is an MLP), the methods in this paper can accurately predict the implicit bias of attention trained through gradient descent. Specifically, the general formula in this paper decouples attention weights into two parts: one is a directed part controlled by SVM that selects labels through a 0-1 mask; the other is a finite part that determines the precise composition of selected tokens by adjusting softmax probabilities.
An important feature of these findings is their applicability to arbitrary datasets (as long as SVM is feasible) and their numerical validation. The authors extensively validate the maximum margin equivalence and implicit bias of transformers through experiments. They believe these findings contribute to understanding transformers as a hierarchical maximum margin token selection mechanism and lay the groundwork for upcoming research on their optimization and generalization dynamics.
Reference content:
https://news.ycombinator.com/item?id=37367951
https://twitter.com/vboykis/status/1698055632543207862
© THE END
Please contact this public account for authorization
Submissions or inquiries: [email protected]