Source: Deephub Imba
This article is approximately 6500 words long and is recommended for a 10-minute read. This article will delve into how TurboAttention achieves efficiency improvements from a technical perspective and analyze its architectural innovations.
As large language models (LLMs) continue to evolve in the AI application domain, their computational costs are also showing a significant upward trend. Data analysis indicates that the operational cost of GPT-4 is approximately $700/hour, with total spending by enterprises on LLM inference exceeding $5 billion in 2023. The core challenge lies in the attention mechanism—this mechanism is the computational core for the model’s processing and correlation of information, and it also constitutes the main performance bottleneck.
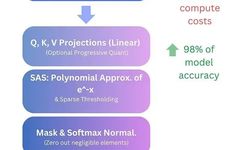
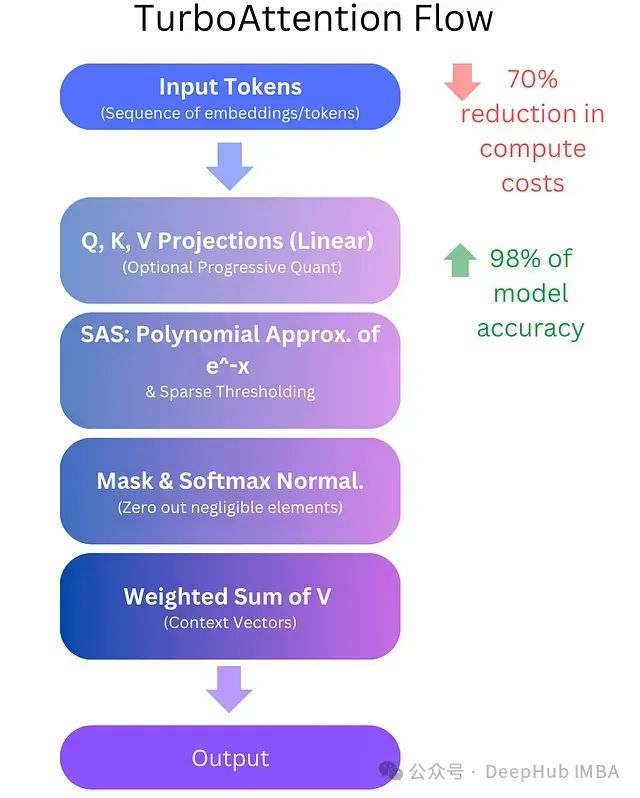
TurboAttention proposes a novel method for LLM information processing. This method replaces the traditional quadratic complexity attention mechanism with a series of optimization techniques, including sparse polynomial softmax approximation and efficient quantization technology. Preliminary results show that this method can achieve a 70% reduction in computational costs while maintaining 98% model accuracy.
For organizations deploying large-scale LLMs, this is not only a performance enhancement but also a significant technological breakthrough that can greatly reduce operational costs and optimize response times.
This article will delve into how TurboAttention achieves efficiency improvements from a technical perspective and analyze its architectural innovations.
1. Principles of Attention Mechanism
Before delving into TurboAttention, it is essential to understand the basic principles of the attention mechanism, especially its dual characteristics of efficiency and computational intensity.
Definition of Attention Mechanism
In the field of deep learning, the attention mechanism is a technique that enables the model to dynamically focus on different parts of the input data. Unlike assigning the same weight to all tokens or elements, the attention mechanism allows the network to emphasize specific tokens. This characteristic is particularly important in sequence processing tasks, such as the influence of earlier words in a sentence on subsequent words in language modeling.
Types of Attention Mechanism
Self-Attention: Computes attention scores within the same sequence. For example, in sentence processing, the model calculates the relevance of each word to other words in the same sentence to capture contextual relationships.
Cross-Attention: Computes attention scores between different sequences, typically applied in neural machine translation systems for calculating the correlation between source language and target language sequences.
Computational Complexity Analysis
The traditional attention mechanism requires processing matrix calculations of size, where represents the sequence length. Therefore, the computational complexity is. For sequences of several thousand tokens common in LLMs, this complexity rapidly becomes a performance bottleneck.
The Necessity of Efficient Attention Mechanism
As model sizes expand from millions to billions or even trillions of parameters, the computational bottleneck of the attention mechanism becomes increasingly prominent, severely limiting real-time processing capabilities and leading to rising computational costs. TurboAttention addresses this issue by integrating multiple optimization strategies, including sparsification, polynomial softmax approximation, and progressive quantization schemes.
2. TurboAttention Technical Architecture
TurboAttention provides a technical solution for approximating the attention mechanism in large-scale Transformer models, achieving a balance between computational efficiency and model performance. Its core innovations include two aspects: optimization of attention weight computation (using polynomial approximation and sparse threshold processing) and optimization of related data (query, key, and value matrices) storage (using progressive quantization schemes).
Core Technical Components
5. Progressive Quantization (PQ): Implements a multi-level quantization strategy (from INT8 to INT4, and in some cases down to INT2), optimizing bandwidth and memory usage.
Mathematical Foundation
The mathematical expression for traditional attention operations is:
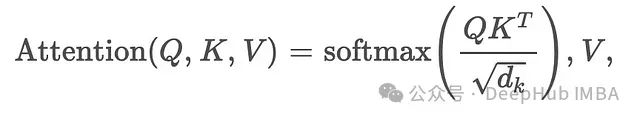
where (query matrix), (key matrix), and (value matrix) are generated from the input data, representing the key vector dimension. While ensuring that the attention weights sum to 1, the exponential operations incur significant computational overhead. TurboAttention optimizes this process by introducing sparse computations (only calculating necessary attention scores) and efficient exponential approximations.
Storing and transmitting matrices in high precision (FP16/FP32) consumes a significant amount of memory. Progressive quantization addresses this issue by converting these matrices into low-bit integer representations, effectively reducing memory and computational overhead.
SAS: Sparse Activation Softmax Technology
A key performance bottleneck of the attention mechanism in Transformer models is the softmax function. Traditional softmax computation requires executing exponential and division operations, which can generate significant floating-point operation overhead when dealing with large matrices.
Polynomial Approximation of Softmax
SAS (Sparse Activation Softmax) technology has demonstrated that effective approximations can be achieved using low-degree polynomials within practical application ranges. The specific definition is as follows:
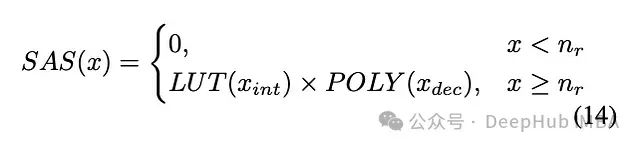
This formula divides the computation into integer and fractional parts (and), using a lookup table (LUT) for one part and polynomial () for the other part.
A typical cubic polynomial fitting (solved by the least squares method) is as follows:

By limiting the polynomial degree to 2 or 3 and controlling the value range within, the SAS method achieves significant performance improvements compared to floating-point exponential operations.
On hardware such as GPU tensor cores, these polynomial operations can be executed in an FP16-friendly manner, further increasing computational throughput.
Sparse Processing After Softmax
Large “dominant” attention scores often overshadow smaller scores. After applying polynomial exponential approximation, SAS can zero out scores below a threshold, achieving the goal of focusing only on the most relevant token interactions. This method generates sparse results, thereby reducing memory and computational overhead.
Progressive Quantization Technology (PQ)
SAS technology solves the computational efficiency problem of softmax, while quantization technology provides solutions for memory bandwidth constraints in large-scale models. Traditional integer quantization methods have proven effective in processing weights and activation values, but most methods still require partial dequantization operations for query (Q), key (K), and value (V) matrices when applying the attention mechanism.

Progressive Quantization (PQ) technology originates from recent research works (such as Qserve proposed by Lin et al. in 2024) and adopts a two-level processing scheme:
First Level: Symmetric INT8 Quantization
Maps original FP16 or FP32 values to the INT8 range with a zero point to avoid extra computational overhead in matrix multiplication. This phase also preserves the scale factor (floating-point value) and the quantized integer data.
Second Level: Asymmetric INT4 Quantization
Further compresses the INT8 representation to INT4 precision, requiring the introduction of a zero point. Although asymmetric quantization introduces additional terms in multiplication, since most data is processed in compressed format, only partial expansion is performed when necessary, effectively controlling overall overhead.
The mathematical expression for progressive quantization is:
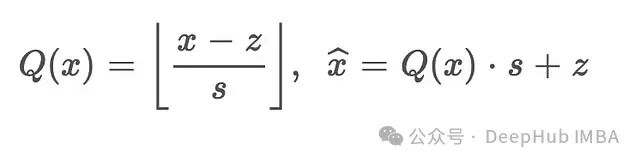
where and can have different values in the INT8 and INT4 stages. The final integer inference computation formula (derived from equations 7 and 8 in the snippet) is:

where and represent partially decompressed but still low-bit representations of data. This series of operations ensures minimal floating-point operation overhead while achieving significant memory savings.
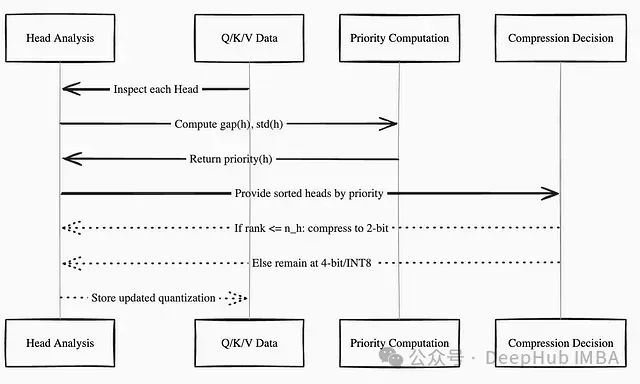
Differentiated Processing of Attention Head Priority
An important finding during the quantization process is that different attention heads exhibit significant differences in sensitivity to accuracy loss. Experimental observations from the Phi3-mini and LLaMA3-8B models indicate that certain attention heads in the query and key matrices have larger magnitudes, and excessive compression of these heads can lead to performance degradation.
To address this issue, TurboAttention introduces an attention head priority computation mechanism:
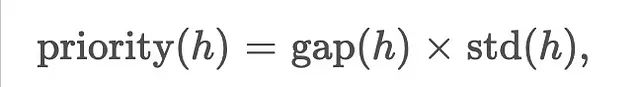
where represents the difference between the maximum and minimum values in a head, which is the standard deviation of these differences. Heads with higher priorities are more sensitive to low-bit quantization, thus maintaining INT4 precision, while lower-priority heads can be further compressed to INT2. The specific implementation is:
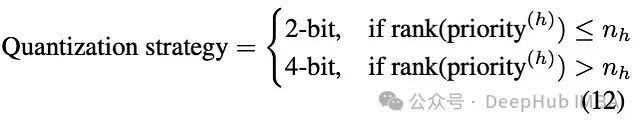
By this means, a small number of heads (defined by parameters) undergo more aggressive compression, while maintaining the overall performance of the model. This refined quantization strategy achieves better compression results compared to uniform quantization schemes.
3. TurboAttention Implementation Architecture
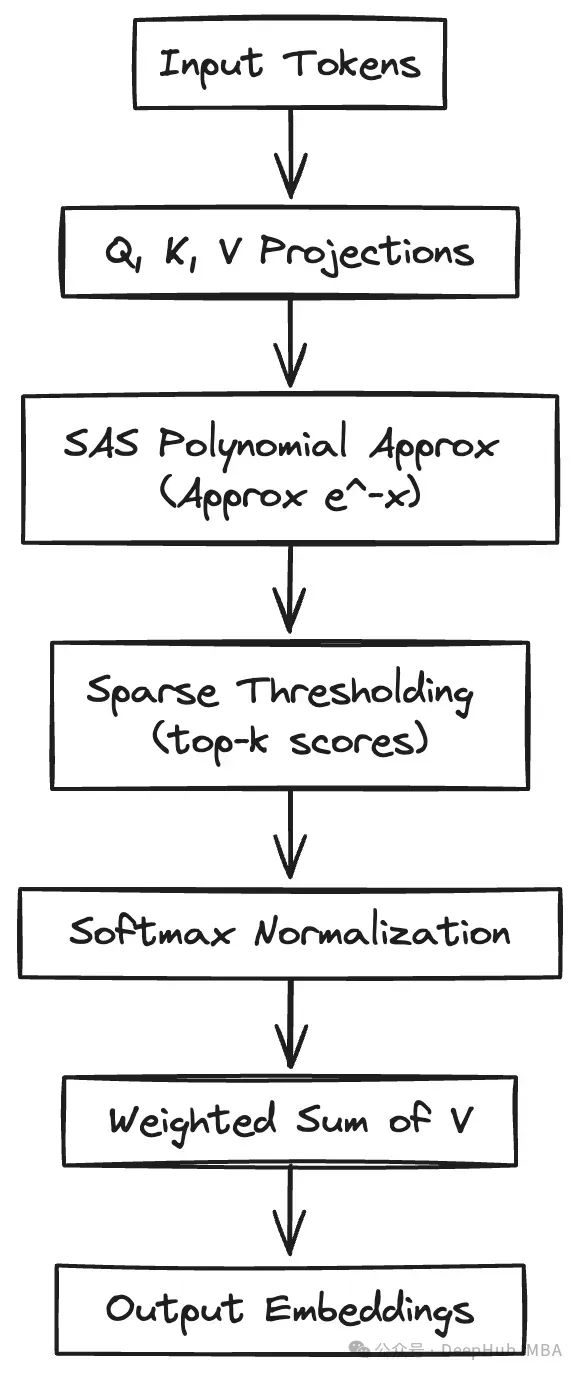
The implementation of TurboAttention involves multiple core modules: the polynomial-based softmax approximation module and the progressive quantization processing module for Q, K, and V matrices. Below is a PyTorch-based implementation example.
The implementation of TurboAttention involves multiple core modules: the polynomial-based softmax approximation module and the progressive quantization processing module for Q, K, and V matrices. Below is a PyTorch-based implementation example.
Note: The example code integrates core ideas such as sparse attention, polynomial exponential approximation, and partial quantization. To maintain code readability, some implementation details (such as the specific implementation of polynomial approximation) have been appropriately simplified.
import torch import torch.nn as nn import torch.nn.functional as F import math class TurboAttention(nn.Module): def __init__(self, embed_dim, num_heads, sparse_ratio=0.1): super(TurboAttention, self).__init__() self.embed_dim = embed_dim self.num_heads = num_heads self.sparse_ratio = sparse_ratio self.head_dim = embed_dim // num_heads assert ( self.head_dim * num_heads == embed_dim ), "Embedding dimension must be divisible by the number of attention heads" # Define linear projection layers self.q_proj = nn.Linear(embed_dim, embed_dim) self.k_proj = nn.Linear(embed_dim, embed_dim) self.v_proj = nn.Linear(embed_dim, embed_dim) # Define output projection layer self.out_proj = nn.Linear(embed_dim, embed_dim) # Define polynomial coefficients for e^-x approximation (SAS) # P(x) = a3*x^3 + a2*x^2 + a1*x + a0 self.poly_a3 = -0.1025 self.poly_a2 = 0.4626 self.poly_a1 = -0.9922 self.poly_a0 = 0.9996 def forward(self, x): batch_size, seq_length, embed_dim = x.size() # Step 1: Perform linear projections and optionally quantize Q_fp = self.q_proj(x) K_fp = self.k_proj(x) V_fp = self.v_proj(x) # Note: The implementation code for progressive quantization is omitted here # In practical applications, Q, K, V need to be quantized to low-bit formats # and partial dequantization must be performed as needed to support matrix multiplication # Rearrange tensors to support multi-head attention computation Q = Q_fp.view(batch_size, seq_length, self.num_heads, self.head_dim).transpose(1, 2) K = K_fp.view(batch_size, seq_length, self.num_heads, self.head_dim).transpose(1, 2) V = V_fp.view(batch_size, seq_length, self.num_heads, self.head_dim).transpose(1, 2) # Step 2: Compute scaled dot-product attention # Use polynomial approximation to replace the standard exponential function scores = torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(self.head_dim) # Clamp attention scores to [0, 1] range for polynomial computation scores_clamped = torch.clamp(scores, 0, 1) # Use polynomial approximation to compute e^-x # In softmax, use e^score or e^-score based on score sign # Here we show the approximation for e^-x exponent_approx = ( self.poly_a3 * scores_clamped ** 3 + self.poly_a2 * scores_clamped ** 2 + self.poly_a1 * scores_clamped + self.poly_a0 ) # Step 3: Implement top-k sparsification top_k = max(1, int(seq_length * self.sparse_ratio)) top_scores, _ = torch.topk(scores, top_k, dim=-1) threshold = top_scores[:, :, :, -1].unsqueeze(-1) mask = (scores >= threshold) # Convert polynomial approximation results to masked attention distribution exponent_approx = exponent_approx.masked_fill(~mask, float('-inf')) # Step 4: Execute softmax normalization attn = F.softmax(exponent_approx, dim=-1) # Step 5: Apply dropout for regularization attn = F.dropout(attn, p=0.1, training=self.training) # Step 6: Compute attention-weighted sum context = torch.matmul(attn, V) # Restore original tensor shape context = context.transpose(1, 2).contiguous().view(batch_size, seq_length, embed_dim) out = self.out_proj(context) return out
TurboAttention can be integrated into the PyTorch Transformer architecture by replacing the standard multi-head attention module (such as nn.MultiheadAttention):
class TransformerBlock(nn.Module): def __init__(self, embed_dim, num_heads): super(TransformerBlock, self).__init__() self.attention = TurboAttention(embed_dim, num_heads) self.layer_norm1 = nn.LayerNorm(embed_dim) self.feed_forward = nn.Sequential( nn.Linear(embed_dim, embed_dim * 4), nn.ReLU(), nn.Linear(embed_dim * 4, embed_dim) ) self.layer_norm2 = nn.LayerNorm(embed_dim) def forward(self, x): # Attention layer computation attn_out = self.attention(x) x = self.layer_norm1(x + attn_out) # Feed-forward network computation ff_out = self.feed_forward(x) x = self.layer_norm2(x + ff_out) return x
Production Environment Deployment Plan
In engineering practice, in addition to algorithm implementation, the production deployment of TurboAttention also requires robust DevOps support. Key technical aspects include containerization management, service orchestration, and distributed inference workflow design.
Containerization Implementation
Utilizing Docker for environment consistency management: # Base image selection FROM pytorch/pytorch:1.12.1-cuda11.3-cudnn8-runtime
# Environment variable configuration ENV PYTHONDONTWRITEBYTECODE=1 ENV PYTHONUNBUFFERED=1 # Set working directory WORKDIR /app # Install dependencies COPY requirements.txt . RUN pip install --upgrade pip RUN pip install -r requirements.txt # Copy project files COPY . . # Service startup command CMD ["python", "deploy_model.py"]
Example content of the dependency configuration file requirements.txt:
torch==1.12.1 torchvision==0.13.1 flask==2.0.3 gunicorn==20.1.0
Service Orchestration Configuration
Using Kubernetes for automated deployment and elastic scaling:
apiVersion: apps/v1 kind: Deployment metadata: name: turboattention-deployment spec: replicas: 3 selector: matchLabels: app: turboattention template: metadata: labels: app: turboattention spec: containers: - name: turboattention-container image: your-docker-repo/turboattention:latest ports: - containerPort: 8000 resources: limits: memory: "2Gi" cpu: "1" requests: memory: "1Gi" cpu: "0.5" --- apiVersion: v1 kind: Service metadata: name: turboattention-service spec: selector: app: turboattention ports: - protocol: TCP port: 80 targetPort: 8000 type: LoadBalancer
Workflow Automation
Based on Airflow, implement model updates and deployment automation:
from airflow import DAG from airflow.operators.bash import BashOperator from datetime import datetime default_args = { 'owner': 'airflow', 'start_date': datetime(2023, 1, 1), } with DAG('deploy_turboattention', default_args=default_args, schedule_interval='@daily') as dag: build_docker = BashOperator( task_id='build_docker_image', bash_command='docker build -t your-docker-repo/turboattention:latest .' ) push_docker = BashOperator( task_id='push_docker_image', bash_command='docker push your-docker-repo/turboattention:latest' ) update_kubernetes = BashOperator( task_id='update_kubernetes_deployment', bash_command='kubectl apply -f k8s-deployment.yaml' ) # Define task execution order build_docker >> push_docker >> update_kubernetes
**Performance Evaluation Methods**
The performance evaluation of TurboAttention needs to be compared with benchmark attention mechanisms from multiple dimensions, including computational speed, accuracy, memory usage efficiency, and operational stability.
Below is a code example demonstrating a performance testing method based on synthetic data:
import time import torch def benchmark_attention(attention_layer, x): start_time = time.time() for _ in range(100): output = attention_layer(x) end_time = time.time() avg_time = (end_time - start_time) / 100 return avg_time # Construct test data batch_size = 32 seq_length = 512 embed_dim = 1024 x = torch.randn(batch_size, seq_length, embed_dim).cuda() # Standard attention mechanism test standard_attention = nn.MultiheadAttention(embed_dim, num_heads=8).cuda() standard_time = benchmark_attention(standard_attention, x) print(f"Standard attention mechanism average execution time: {standard_time:.6f} seconds") # TurboAttention test turbo_attention = TurboAttention(embed_dim, num_heads=8, sparse_ratio=0.1).cuda() turbo_time = benchmark_attention(turbo_attention, x) print(f"TurboAttention average execution time: {turbo_time:.6f} seconds")
The experimental results show that TurboAttention can achieve a 1.5 to 3 times speedup in inference, with the specific improvement depending on the configuration of several key parameters, such as sparse_ratio (sparsity rate), the polynomial degree of the softmax approximation, and the bit depth settings of progressive quantization. Importantly, this significant performance improvement results in only a minor accuracy loss (typically controlled within 1-2% for specific application scenarios).
4. Benchmark Testing Implementation
Below is a code example demonstrating a performance testing method based on synthetic data:
import timeimport torch def benchmark_attention(attention_layer, x): start_time = time.time() for _ in range(100): output = attention_layer(x) end_time = time.time() avg_time = (end_time - start_time) / 100 return avg_time # Construct test data batch_size = 32 seq_length = 512 embed_dim = 1024 x = torch.randn(batch_size, seq_length, embed_dim).cuda() # Standard attention mechanism test standard_attention = nn.MultiheadAttention(embed_dim, num_heads=8).cuda() standard_time = benchmark_attention(standard_attention, x) print(f"Standard attention mechanism average execution time: {standard_time:.6f} seconds") # TurboAttention test turbo_attention = TurboAttention(embed_dim, num_heads=8, sparse_ratio=0.1).cuda() turbo_time = benchmark_attention(turbo_attention, x) print(f"TurboAttention average execution time: {turbo_time:.6f} seconds")5. Directions for Technical Development
TurboAttention opens up new research directions for optimizing large-scale models:
Adaptive Sparsification Mechanism
Develop a context-based dynamic sparsity adjustment mechanism. Reduce sparsity for more complex input regions while applying more aggressive pruning strategies in simpler areas.
Higher-Order Approximation Methods
Research piecewise polynomials or mixed lookup table schemes to improve the accuracy of exponential function approximations while maintaining computational efficiency.
Cross-Modal Attention Optimization
With the popularity of multimodal models, polynomial approximation methods for different modal features need further optimization.
Hardware Collaborative Design
Next-generation GPUs or AI-specific accelerators could consider directly supporting polynomial approximation calculations and multi-level quantization operations at the hardware level.
Device-Side Learning Optimization
Utilizing the memory efficiency improvements brought by progressive quantization, explore implementing model fine-tuning and personalized adaptation on resource-constrained devices.
Conclusion
TurboAttention achieves significant breakthroughs in optimizing the attention mechanisms of large language and vision models, with core innovations including:
• Differentiated Quantization Strategy: A selective compression scheme based on sensitivity analysis, ensuring that the performance of key attention heads is not affected.
Through these technological innovations, TurboAttention significantly reduces computational and memory overhead while maintaining the core capability of the attention mechanism to capture contextual dependencies.
In engineering practice, supported by modern DevOps toolchains (Docker, Kubernetes, Airflow, etc.), TurboAttention can achieve smooth production environment deployment. As machine learning technologies continue to evolve, such efficient attention mechanisms will play a vital role in reducing the deployment costs of large-scale models. Organizations adopting these optimization techniques can significantly lower hardware investment and energy consumption while maintaining model performance.
Paper:
https://arxiv.org/abs/2412.08585
Author: Tim Urista
About Us
Data Hub THU, as a data science public account, is backed by Tsinghua University’s Big Data Research Center, sharing cutting-edge data science and big data technology innovation research dynamics, continuously disseminating data science knowledge, and striving to build a platform for data talent aggregation, creating the strongest group in China’s big data.

Sina Weibo: @Data Hub THU
WeChat Video Number: Data Hub THU
Today’s Headlines: Data Hub THU