Skip to content
Lightning Attention-2 is a new type of linear attention mechanism that aligns the training and inference costs of long sequences with those of a 1K sequence length.
The limitations on sequence length in large language models greatly restrict their applications in the field of artificial intelligence, such as multi-turn dialogue, long text understanding, and the processing and generation of multimodal data. The fundamental reason for this limitation lies in the quadratic computational complexity of the Transformer architecture currently used by all large language models concerning sequence length. This means that as the sequence length increases, the required computational resources increase geometrically. Efficiently handling long sequences has been one of the challenges for large language models.
Previous methods often focused on how to adapt large language models to longer sequences during the inference phase. For example, using Alibi or similar relative position encoding methods to allow the model to adapt to different input sequence lengths, or using interpolation on relative position encodings like RoPE to further fine-tune an already trained model to achieve extended sequence lengths. These methods only provided large models with some capability for long sequence modeling, but did not reduce the actual training and inference costs.
The OpenNLPLab team attempted to solve the long sequence problem in large language models once and for all. They proposed and open-sourced Lightning Attention-2—a new type of linear attention mechanism that aligns the training and inference costs of long sequences with those of a 1K sequence length. Before encountering GPU memory bottlenecks, indefinitely increasing the sequence length does not negatively impact the model training speed. This makes unlimited length pre-training possible. Meanwhile, the inference cost for ultra-long texts is consistent with or even less than that of 1K tokens, which will greatly reduce the current inference costs of large language models. As shown in the figure below, with model sizes of 400M, 1B, and 3B, as the sequence length increases, the training speed of LLaMA enhanced by FlashAttention2 begins to decline rapidly, while the speed of TansNormerLLM enhanced by Lightning Attention-2 remains almost unchanged.


-
Paper: Lightning Attention-2: A Free Lunch for Handling Unlimited Sequence Lengths in Large Language Models
-
Paper Address: https://arxiv.org/pdf/2401.04658.pdf
-
Open Source Address: https://github.com/OpenNLPLab/lightning-attention
Introduction to Lightning Attention-2
Maintaining consistent pre-training speeds for large models across different sequence lengths sounds like an impossible task. In fact, if an attention mechanism’s computational complexity remains linear concerning sequence length, this can be achieved. Since the advent of linear attention in 2020, researchers have been striving to ensure that the practical efficiency of linear attention aligns with its theoretical linear computational complexity. Before 2023, most works on linear attention focused on aligning their accuracy with that of Transformers. Finally, in mid-2023, improved linear attention mechanisms were able to match the accuracy of state-of-the-art Transformer architectures. However, the key computational trick that transforms the computational complexity of linear attention from quadratic to linear, termed ‘right multiplication’, is much slower in practical implementations than direct left multiplication algorithms. The reason lies in the right multiplication’s requirement for cumulative summation (cumsum) involving many loop operations, leading to a significantly lower efficiency compared to left multiplication due to extensive I/O operations.
To better understand the ideas behind Lightning Attention-2, let’s first review the traditional softmax attention computation formula: O=softmax ((QK^T)⊙M_) V, where Q, K, V, M, and O represent the query, key, value, mask, and output matrices, respectively. Here, M is a lower triangular matrix of all 1s in unidirectional tasks (like GPT), and can be ignored in bidirectional tasks (like Bert), meaning bidirectional tasks do not have a mask matrix.
The author summarizes the overall ideas of Lightning Attention-2 into the following three points for explanation:
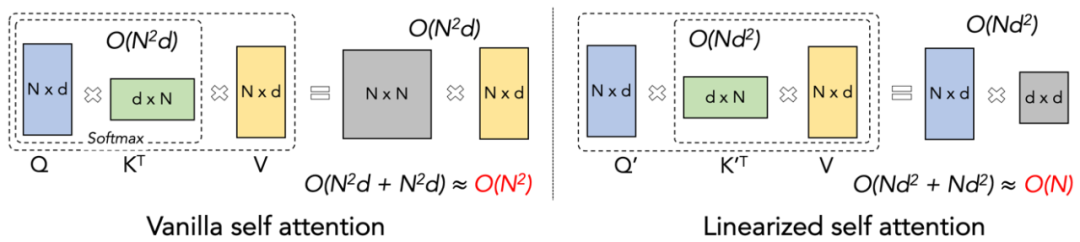
1. One of the core ideas of Linear Attention is to eliminate the computationally expensive softmax operator, allowing the attention computation formula to be written as O=((QK^T)⊙M_) V. However, due to the existence of the mask matrix M in unidirectional tasks, this form can still only perform left multiplication, thus not achieving O (N) complexity. For bidirectional tasks, since there is no mask matrix, the Linear Attention computation formula can be further simplified to O=(QK^T) V. The cleverness of Linear Attention lies in the fact that by simply utilizing the associative property of matrix multiplication, its computation formula can be further transformed to: O=Q (K^T V), where this computation form is called right multiplication, and the former is left multiplication. As shown in Figure 2, it can be intuitively understood that Linear Attention can achieve an attractive O (N) complexity in bidirectional tasks!
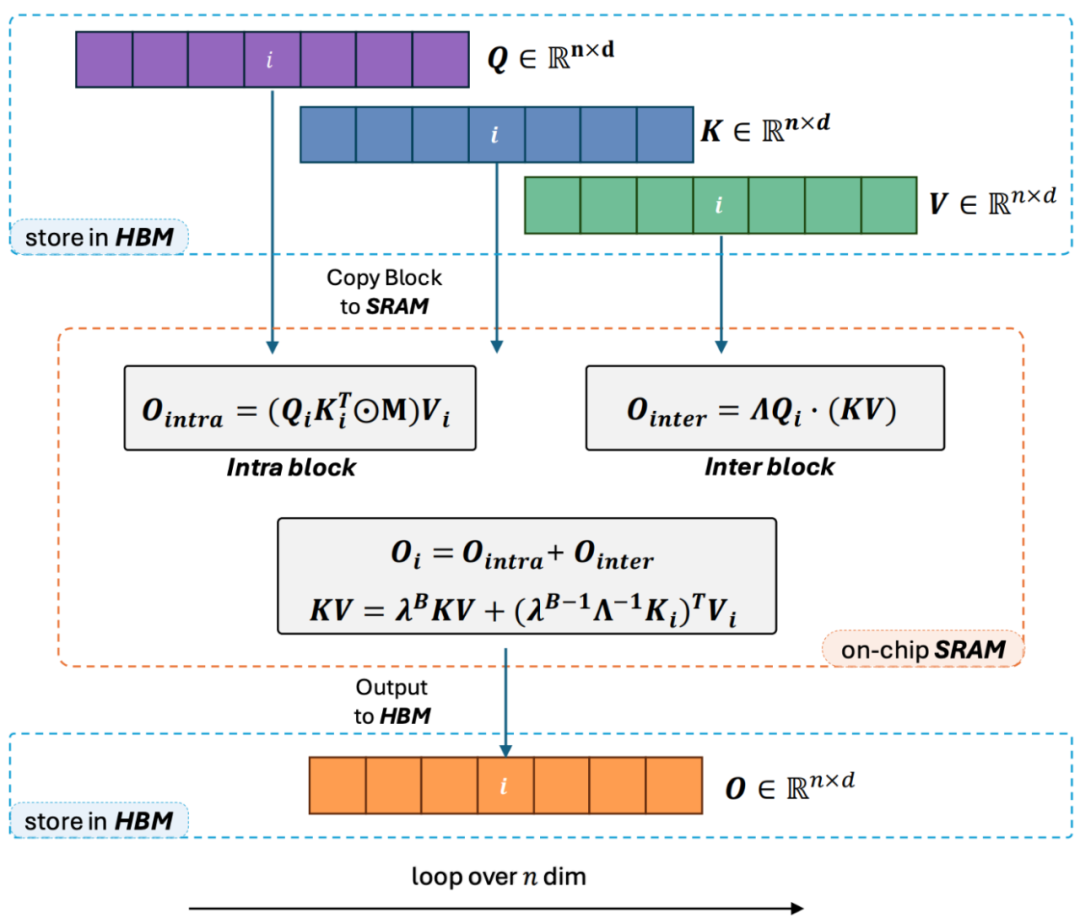
2. However, as decoder-only GPT-style models gradually become the de facto standard for LLMs, how to leverage the right multiplication property of Linear Attention to accelerate unidirectional tasks has become an urgent problem to solve. To address this, the author proposes using a ‘divide and conquer’ approach to split the computation of the attention matrix into diagonal and non-diagonal forms, and to compute them using different methods. As shown in Figure 3, Linear Attention-2 utilizes the common Tiling concept in computer science, dividing the Q, K, and V matrices into an equal number of blocks. The intra-block computation of each block, due to the presence of the mask matrix, still retains the left multiplication method, exhibiting O (N^2) complexity; while the inter-block computation, due to the absence of the mask matrix, can utilize the right multiplication method, thus enjoying O (N) complexity. After computing both separately, the corresponding Linear Attention output Oi for the i-th block can be obtained by direct addition. Furthermore, the states of KV are accumulated using cumsum for use in the next block’s computation. This leads to the overall algorithm complexity of Lightning Attention-2 being a trade-off of intra-block O (N^2) and inter-block O (N). How to achieve a better trade-off is determined by the Tiling block size.
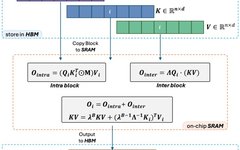
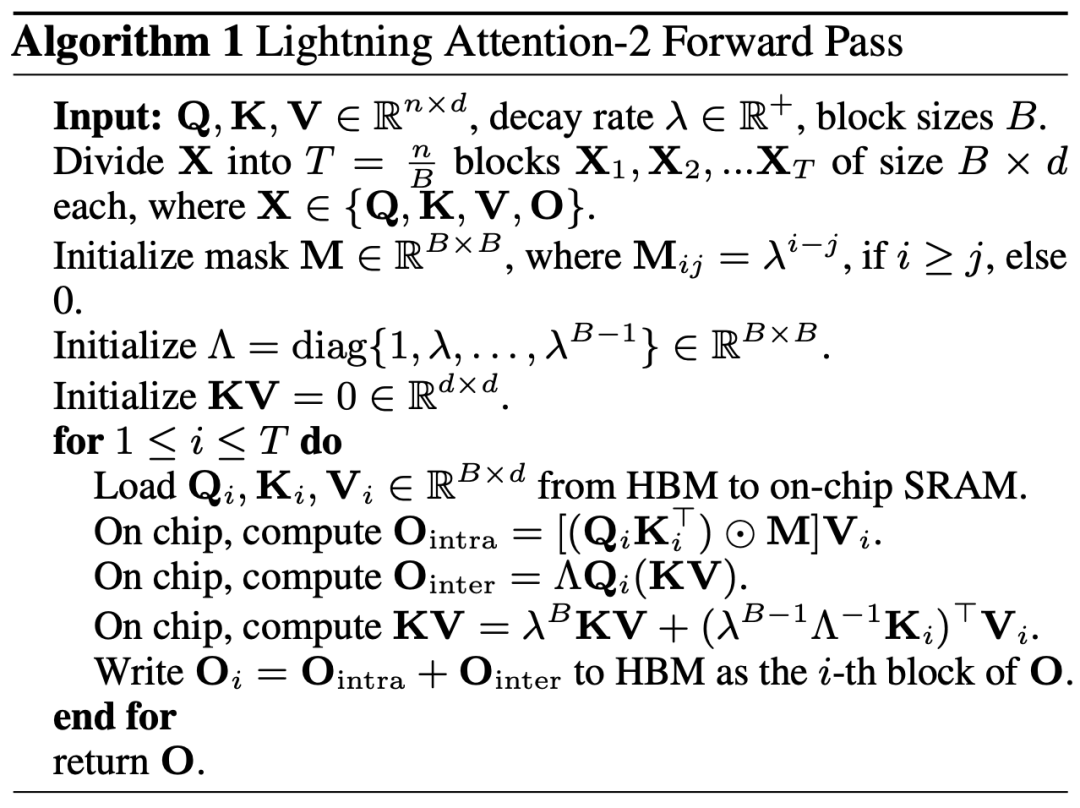
3. Observant readers will notice that the above process only covers the algorithm part of Lightning Attention-2. It is named ‘Lightning’ because the author fully considers the efficiency of this algorithm during GPU hardware execution. Inspired by the FlashAttention series of works, when performing calculations on the GPU, the author transports the split Q_i, K_i, V_i tensors from the slower, larger HBM to the faster, smaller SRAM for computation, thereby reducing significant memory I/O overhead. Once the block completes the Linear Attention computation, its output O_i is transported back to HBM. This process is repeated until all blocks are processed.
Readers interested in more details can carefully read Algorithm 1 and Algorithm 2 in this article, as well as the detailed derivation process in the paper. The algorithms and derivation processes distinguish between the forward and backward processes of Lightning Attention-2, helping readers gain a deeper understanding.

Accuracy Comparison of Lightning Attention-2
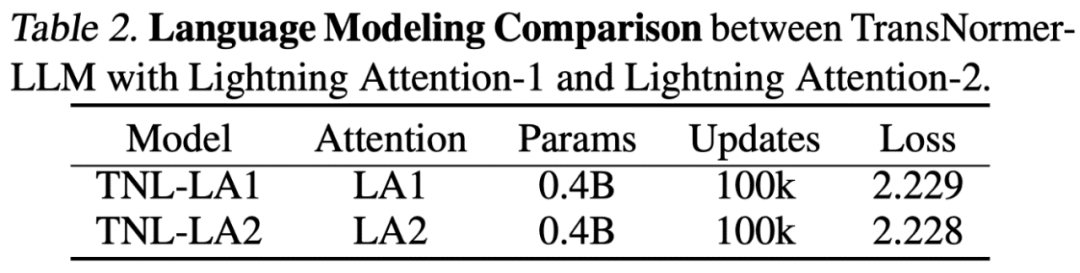
The researchers first compared the accuracy difference between Lightning Attention-2 and Lightning Attention-1 on a small-scale (400M) parameter model, as shown in the figure below, with virtually no difference between the two.
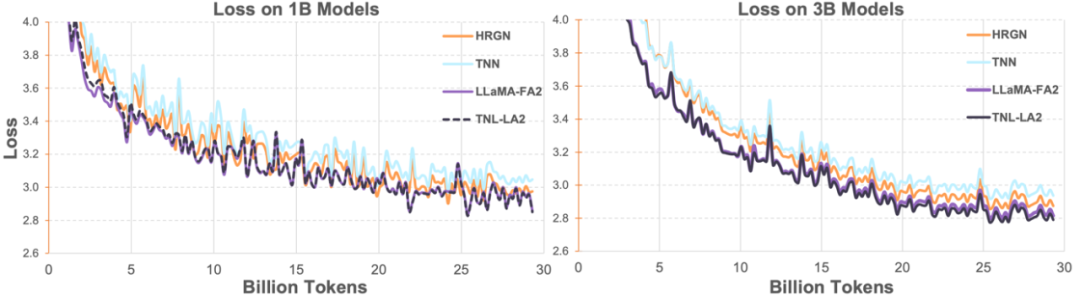
Subsequently, the researchers compared the TransNormerLLM (TNL-LA2) enhanced by Lightning Attention-2 with other advanced non-Transformer architectures and LLaMA enhanced by FlashAttention2 on the same corpus at 1B and 3B scales. As shown in the figure below, TNL-LA2 maintained a similar trend to LLaMA while demonstrating superior loss performance. This experiment indicates that Lightning Attention-2 exhibits accuracy performance comparable to that of state-of-the-art Transformer architectures in language modeling.
In large language model tasks, the researchers compared the TNL-LA2 15B with Pythia on common benchmarks for large models at similar sizes. As shown in the table below, under the condition of consuming the same tokens, TNL-LA2 slightly outperformed the Pythia model based on softmax attention in commonsense reasoning and multiple-choice comprehension capabilities.

Speed Comparison of Lightning Attention-2
The researchers compared the speed and memory usage of Lightning Attention-2 with FlashAttention2 on a single module basis. As shown in the figure below, compared to Lightning Attention-1 and FlashAttention2, Lightning Attention-2 exhibited strictly linear growth concerning sequence length in terms of speed. In terms of memory usage, all three showed similar trends, but Lightning Attention-2 had lower memory usage. This is because the memory usage of FlashAttention2 and Lightning Attention-1 is also approximately linear.
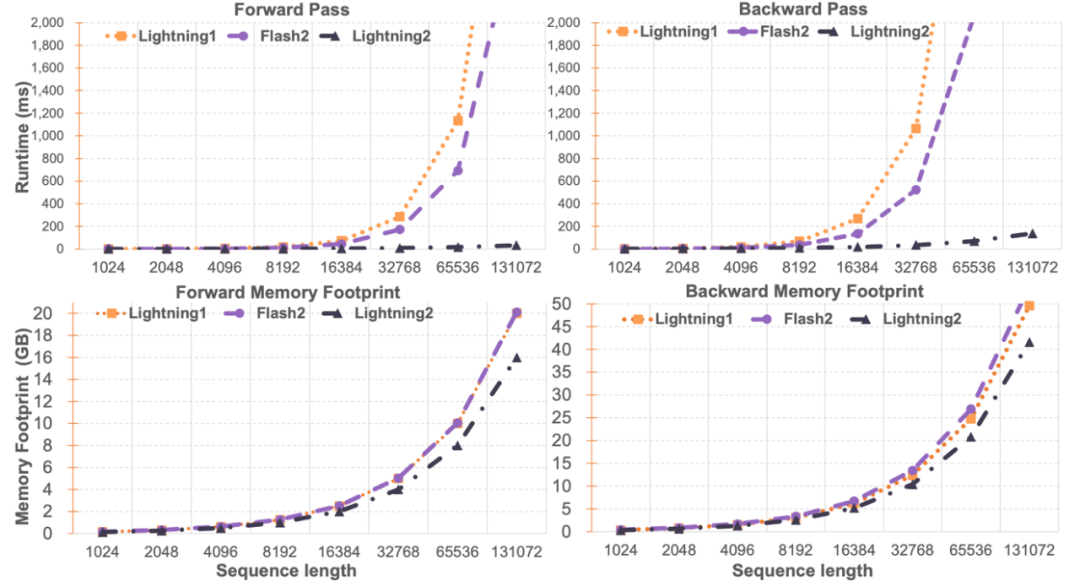
The author notes that this article primarily focuses on solving the training speed of linear attention networks, achieving training speeds for arbitrary length sequences similar to those of 1K sequences. There is not much introduction regarding inference speed. This is because linear attention can be losslessly transformed into RNN mode during inference, achieving similar results, meaning that the inference speed for a single token remains constant. In contrast, for Transformers, the inference speed of the current token is related to the number of previous tokens.
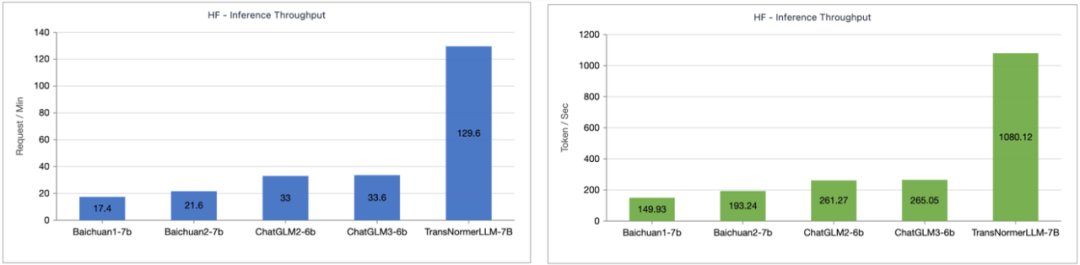
The author tested the inference speed comparison between TransNormerLLM-7B enhanced by Lightning Attention-1 and common 7B models. As shown in the figure below, under similar parameter sizes, the throughput speed of Lightning Attention-1 is four times that of Baichuan and over 3.5 times that of ChatGLM, demonstrating excellent inference speed advantages.
Lightning Attention-2 represents a significant advancement in linear attention mechanisms, allowing it to perfectly replace traditional softmax attention in terms of both accuracy and speed, providing a sustainable scalability capability for increasingly larger models, and offering a pathway to process infinitely long sequences more efficiently. The OpenNLPLab team will continue to research sequence parallel algorithms based on linear attention mechanisms to address the current memory barrier issues.