In-Depth Analysis of Self-Attention from Source Code

Reprinted from | PaperWeekly

©PaperWeekly Original · Author｜Hai Chenwei

School｜Master’s student at Tongji University

Research Direction｜Natural Language Processing

1. What is the core of Self-Attention?

The core of Self-Attention is to enhance the semantic representation of the target word using other words in the text, thereby better utilizing contextual information.

2. How is the time complexity of Self-Attention calculated?

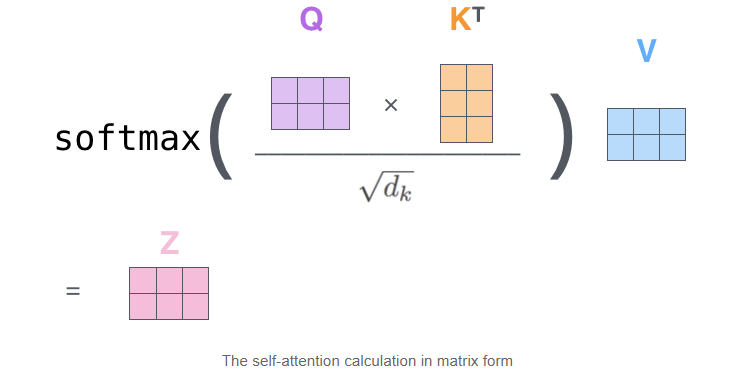
Their respective time complexities are:

Here we also mention the Multi-Head Attention in the Transformer, which is a combination of multiple Self-Attentions, serving a similar purpose to multiple kernels in CNNs.

The implementation of multi-head is not through looping to compute each head but is accomplished through transposes and reshapes using matrix multiplication.

In practice, the multi-headed attention is done with transposes and reshapes rather than actual separate tensors. —— From Google BERT source code comments

hidden_size (d) = num_attention_heads (m) * attention_head_size (a), which means d=m*a.

For tensor multiplication time complexity analysis, see: Analysis of Matrix and Tensor Multiplication Time Complexity [1].

3. What happens if we don’t multiply the QKV parameter matrices in self-attention?

For the Attention mechanism, it can be explained using a unified query/key/value model, and for self-attention, it is generally said that q=k=v, where equality actually means they come from the same base vector. However, in actual computation, they are different because all three are multiplied by the QKV parameter matrices. If not multiplied, the q, k, v corresponding to each word would be exactly the same.

In self-attention, each word in the sequence computes the dot product with every other word in the sequence, including itself.

Under the same magnitude, the dot product value of qi and ki will be the largest (this can be analogized from the “given the same sum, the product is maximized when the two numbers are equal”).

Thus, in the weighted average after softmax, the weight of the word itself will be the largest, making the weights of other words very small, which cannot effectively utilize contextual information to enhance the semantic representation of the current word.

Multiplying by the QKV parameter matrices makes the q, k, v of each word different, significantly alleviating the above impact.

Of course, the QKV parameter matrices also enable multi-head attention, similar to multiple kernels in CNNs, to capture richer features/information.

4. In regular attention, k=v is generally the case; can self-attention do this?

Self-attention is actually just a special case of attention, so k=v is not a problem, meaning the K and V parameter matrices are the same.

When extending to Multi-Head Attention, after multiplying by the Q and K parameter matrices, the difference between the heads is already guaranteed. After obtaining similarity through the dot product of q and k + softmax, from the perspective of regular attention, it seems more reasonable to multiply by v, which is equal to k.

In Transformer/BERT, completely independent QKV parameter matrices can expand the model’s capacity and expressiveness.

However, adopting a parameter pattern where Q and K=V is also acceptable, as it can reduce model parameters without affecting multi-head implementation.

Source Code

In the entire Transformer/BERT code, the (Multi-Head Scaled Dot-Product) Self-Attention part is relatively the most complex and is the essence of Transformer/BERT. Here is the PyTorch version of the implementation [2], with important code commented and dimension explanations provided.

Without further ado, here are the three main parts:

Initialization: Including the number of heads, size of each head, and initializing the three parameter matrices QKV.

class SelfAttention(nn.Module):
    def __init__(self, config):
        super(SelfAttention, self).__init__()
        if config.hidden_size % config.num_attention_heads != 0:
            raise ValueError(
                "The hidden size (%d) is not a multiple of the number of attention "
                "heads (%d)" % (config.hidden_size, config.num_attention_heads))
        # In Transformer/BERT, all_head_size equals config.hidden_size
        # This is a simplification to keep the dimensions consistent from embedding to final output
        # Thus, multiple attention heads combined still have the dimension of config.hidden_size
        # while attention_head_size is the dimension of each attention head, which must be divisible
        self.num_attention_heads = config.num_attention_heads
        self.attention_head_size = int(config.hidden_size / config.num_attention_heads)
        self.all_head_size = self.num_attention_heads * self.attention_head_size

        # Three parameter matrices
        self.query = nn.Linear(config.hidden_size, self.all_head_size)
        self.key = nn.Linear(config.hidden_size, self.all_head_size)
        self.value = nn.Linear(config.hidden_size, self.all_head_size)

        self.dropout = nn.Dropout(config.attention_probs_dropout_prob)

    def transpose_for_scores(self, x):
        """
        shape of x: batch_size * seq_length * hidden_size
        This operation decomposes hidden_size into self.num_attention_heads * self.attention_head_size
        and then swaps the seq_length dimension and num_attention_heads dimension
        Why do this: because attention computes the dot product of each word in query with each word in key, which is along the seq_length dimension
        The dot product of query and key is [seq_length * attention_head_size] * [attention_head_size * seq_length]=[seq_length * seq_length]
        """
        # Here is a dimension concatenation: (1,2)+(3,4) -> (1, 2, 3, 4)
        new_x_shape = x.size()[:-1] + (self.num_attention_heads, self.attention_head_size)
        x = x.view(*new_x_shape)
        return x.permute(0, 2, 1, 3)

 def forward(self, hidden_states, attention_mask):
        # shape of hidden_states and mixed_*_layer: batch_size * seq_length * hidden_size
        mixed_query_layer = self.query(hidden_states)
        mixed_key_layer = self.key(hidden_states)
        mixed_value_layer = self.value(hidden_states)

        # shape of *_layer: batch_size * num_attention_heads * seq_length * attention_head_size
        query_layer = self.transpose_for_scores(mixed_query_layer)
        key_layer = self.transpose_for_scores(mixed_key_layer)
        value_layer = self.transpose_for_scores(mixed_value_layer)

        # Take the dot product between "query" and "key" to get the raw attention scores.
        # shape of attention_scores: batch_size * num_attention_heads * seq_length * seq_length
        attention_scores = torch.matmul(query_layer, key_layer.transpose(-1, -2))

        # Here is the Scaled operation, normalizing variance to 1 to avoid dimensional effects
        attention_scores /= math.sqrt(self.attention_head_size)

        # shape of attention_mask: batch_size * 1 * 1 * seq_length. It can be automatically broadcasted to the same dimensions as attention_scores
        # The initial input attention_mask is: batch_size * seq_length, after two unsqueeze it becomes the current attention_mask
        attention_scores = attention_scores + attention_mask

        # Normalize the attention scores to probabilities. Softmax does not change dimensions
        # shape of attention_scores: batch_size * num_attention_heads * seq_length * seq_length
        attention_probs = nn.Softmax(dim=-1)(attention_scores)
        attention_probs = self.dropout(attention_probs)

        # shape of value_layer: batch_size * num_attention_heads * seq_length * attention_head_size
        # shape of first context_layer: batch_size * num_attention_heads * seq_length * attention_head_size
        # shape of second context_layer: batch_size * seq_length * num_attention_heads * attention_head_size
        # context_layer dimensions restored to: batch_size * seq_length * hidden_size
        context_layer = torch.matmul(attention_probs, value_layer)
        context_layer = context_layer.permute(0, 2, 1, 3).contiguous()
        new_context_layer_shape = context_layer.size()[:-2] + (self.all_head_size,)
        context_layer = context_layer.view(*new_context_layer_shape)
        return context_layer

Attention is all you need! I hope this article helps you gain a deeper understanding of Self-Attention.

References

Download 1: Four Essentials
Reply "Four Essentials" in the backend of the Machine Learning Algorithms and Natural Language Processing public account to obtain the learning essentials for TensorFlow, Pytorch, Machine Learning, and Deep Learning!

Download 2: Repository Address Sharing
Reply "Code" in the backend of the Machine Learning Algorithms and Natural Language Processing public account to access 195 papers from NAACL + 295 papers from ACL2019 that have open-source code. The open-source address is as follows: https://github.com/yizhen20133868/NLP-Conferences-Code

Heavyweight! The Machine Learning Algorithms and Natural Language Processing exchange group has officially been established! There are abundant resources in the group, and everyone is welcome to join for learning!

Additional free resources! Deep Learning and Neural Networks, Official Chinese Tutorial for Pytorch, Data Analysis using Python, Machine Learning Notes, Official Chinese Documentation for Pandas, Effective Java (Chinese version), and 20 other free resources.

How to obtain: After entering the group, click on the group announcement to obtain the download link.
Note: Please modify the remarks when adding to [School/Company + Name + Direction].
For example — Harbin Institute of Technology + Zhang San + Dialogue System.
The account owner and micro-businesses, please consciously avoid. Thank you!

Recommended Reading:
12 Golden Rules for Solving NER Problems in Industry
Three Steps to Master the Core of Machine Learning: Matrix Derivatives
Distillation Techniques in Neural Networks, Starting from Softmax