Madio.net
Mathematics China
///Editor: Only tulips’ garden
Neural networks are a clever combination of linear and nonlinear modules. When we wisely choose and connect them, we have a powerful tool to approximate any mathematical function. For example, using nonlinear decision boundaries for classification.
The backpropagation technique is responsible for updating the trainable parameters. Although it has intuitive and modular characteristics, this concept is not always deeply explained. Let’s build a neural network from scratch and see the internal workings of neural networks, where we will analogize modules to Lego blocks, stacking one block at a time.
The code to implement this functionality can be found in this repository:
https://github.com/omar-florez/scratch_mlp
Neural Networks as a Component
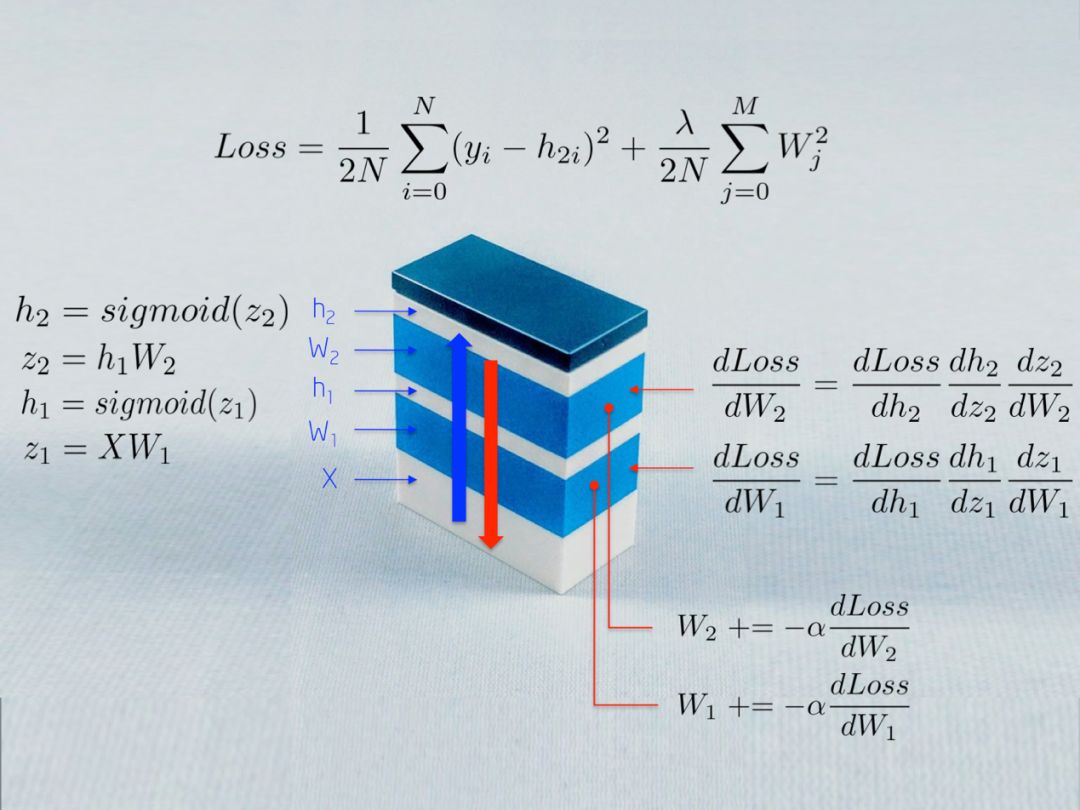
The above figure describes some mathematical formulas used to train neural networks. In this article, we will explain them. Readers may find it interesting that neural networks are a combination of modules connected for different purposes.
Why Read This Document
If you understand the internal structure of neural networks, you will quickly know what to change first when the model does not work, and define a strategy to test the invariants and expected behaviors of the algorithms you know. This will also be very helpful when you want to create and implement new features in the ML library you are using.
Debugging machine learning models is a complex task. In practice, the mathematical models do not work as expected on the first attempt. They may have lower accuracy on new data, cause you to spend longer training times or excessive memory, return a lot of erroneous values or NaN, etc. It becomes convenient when you know how these algorithms work, for example:
-
If the training time is too long, increasing the minibatch size to reduce the variance of observations may help the algorithm converge.
-
If you get NaN predictions, the algorithm may have a gradient that is too large, causing memory overflow. Think of it as continuous matrix multiplication after several iterations. Lowering the learning rate will reduce these values. Reducing the number of layers will decrease the number of multiplications. Clipping gradients will explicitly control this issue.
Specific Example: Learning the XOR Function
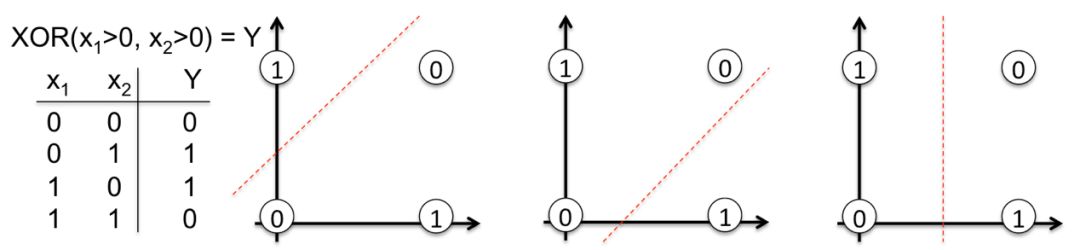
Let’s open the black box. Now we will build a neural network from scratch to learn the XOR function. The choice of this nonlinear function is by no means random. Without backpropagation, it is difficult to learn to separate classes with a straight line.
To illustrate this important concept, please take a close look at the figure below, which shows how a straight line cannot separate the outputs 0 and 1 of the XOR function. Many real-world problems are also non-linearly separable.
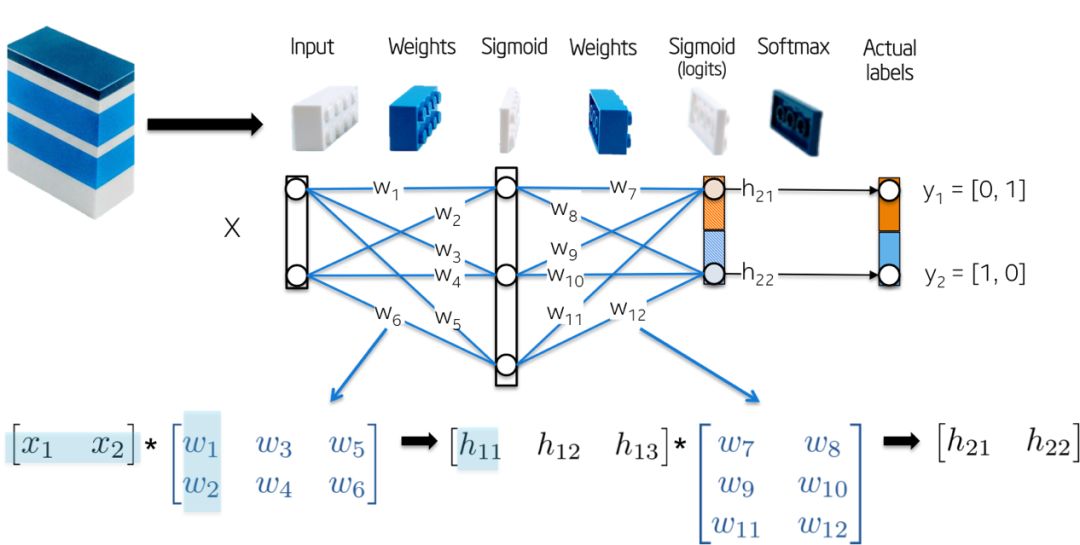
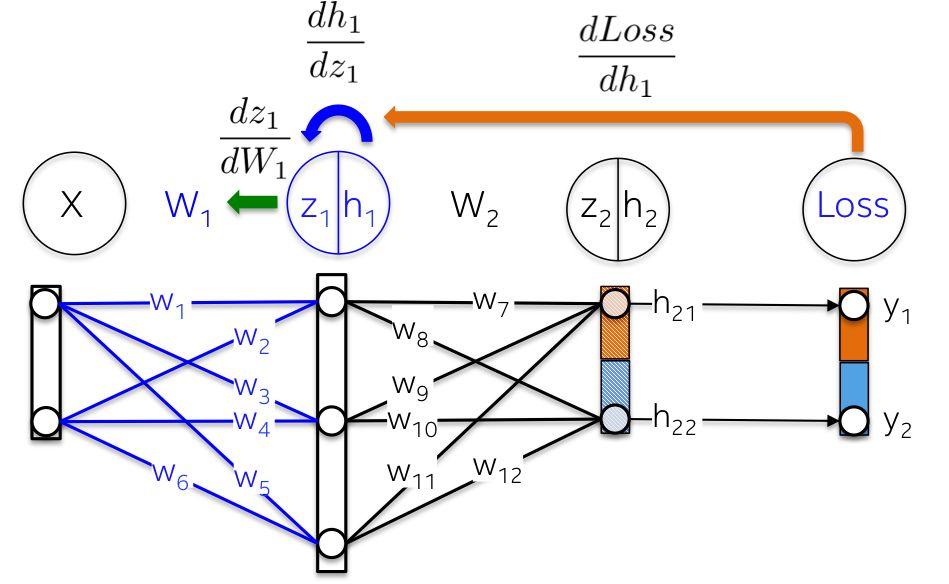
The network topology is very simple:
-Input X is a two-dimensional vector;
-Weight W1 is a 2×3 matrix with randomly initialized values;
-The hidden layer h1 consists of three neurons. Each neuron receives one weighted observation as input, which is highlighted in green in the following figure with the inner product: z1 = [x1, x2][w1, w2];
-Weight W2 is a 3×2 matrix with randomly initialized values;
-The output layer h2 consists of two neurons since the XOR function returns 0 (y1=[0,1]) or 1 (y2 =[1,0]);
More intuitively shown in the figure below:
Now let’s train the model. In our simple example, the trainable parameters are the weights, but note that current research is exploring more types of parameters for optimization. For example, shortcuts between layers, regularization distributions, topologies, residuals, learning rates, etc.
Backpropagation is a method of updating weights in the direction of (gradient) to minimize a predefined error measure (called the loss function) given a batch of labeled observations. It is a special case of a more general technique called automatic differentiation in reverse accumulation mode.
Network Initialization
Let’s initialize the network weights with random numbers.
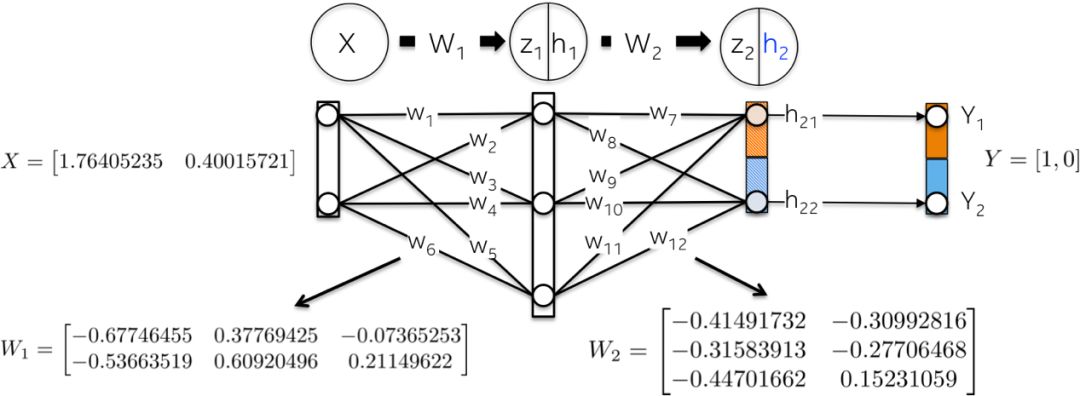
Forward Step
The goal of this step is to propagate the input X forward to each layer of the network until calculating the vector in the output layer h2.
The steps are as follows:
-Using weight W1 as a kernel, linearly map the input data X:

-Use the Sigmoid function to scale this weighted sum z1 to obtain the values of the first hidden layer h1. Note that the original 2-dimensional vector is now mapped to a 3-dimensional space;

-The second layer h2 undergoes a similar process. We first calculate the weighted sum z2 of the first hidden layer, which is now the input data;

-Then calculate their Sigmoid activation function. This vector [0.37166596 0.45414264] represents the log probabilities or prediction vector computed by the network for the given input X;

Computing the Total Loss
Note that the loss function contains a regularization component that penalizes larger weight values like Ridge regression. In other words, larger squared weight values will increase the loss function, which is the error measure we indeed want to minimize.

Backward Step
This step proceeds in reverse order, not forward. First, we calculate the partial derivative of the loss function with respect to the output layer weights (dLoss/dW2), and then calculate the partial derivative for the hidden layer (dLoss/dW1).
(i) dLoss/dW2
The chain rule shows that we can decompose the gradient calculation of the neural network into differentiable parts:
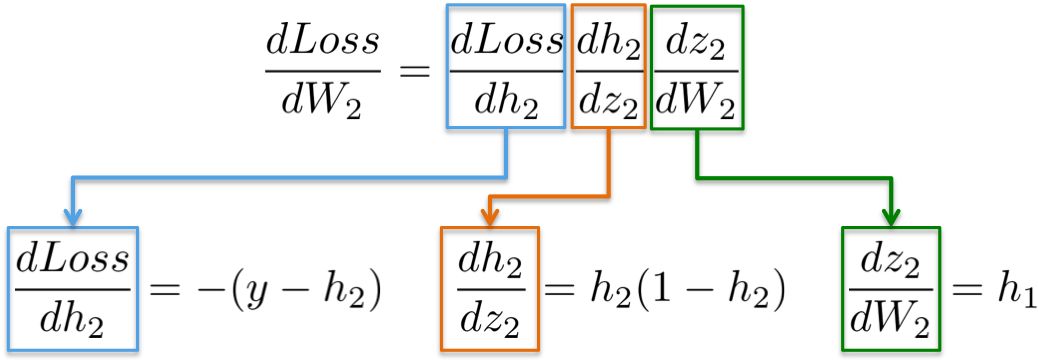
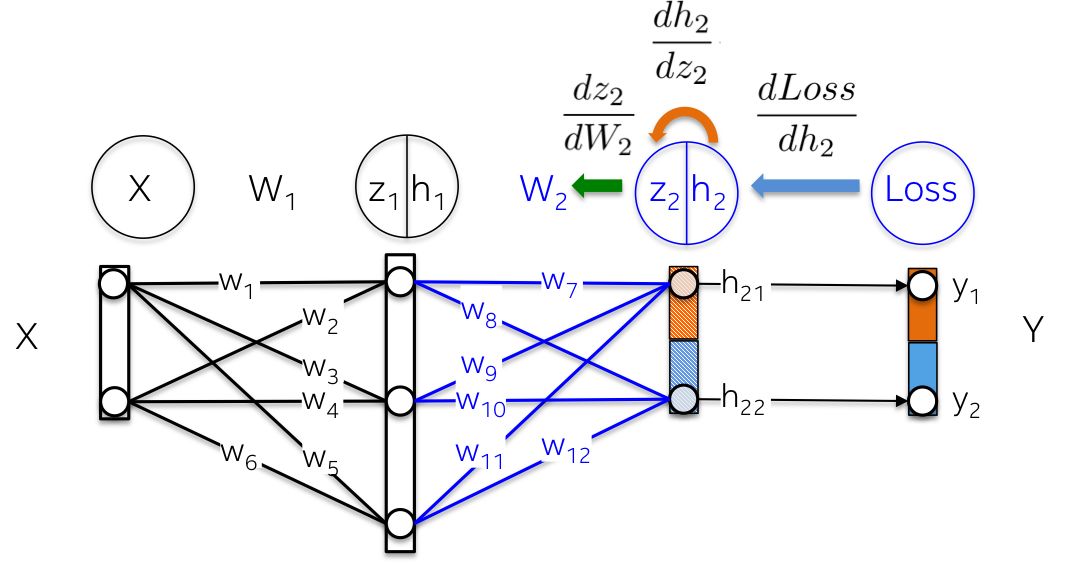
More intuitively, our goal is to update the weights W2 (in blue) in the figure below. To do this, we need to calculate the three partial derivatives along the chain.
Substituting values into these partial derivatives, we can calculate the gradient with respect to the weights W2 as shown below.
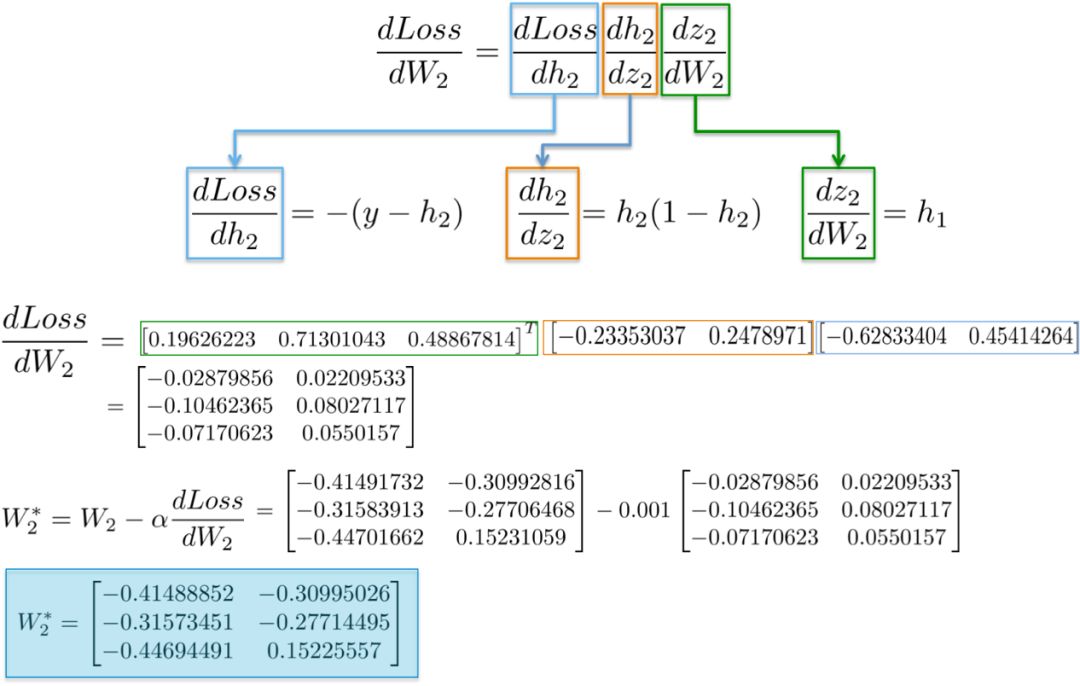
The result is a 3×2 matrix dLoss/dW2, which will update the original W2 values in the direction of minimizing the loss function.
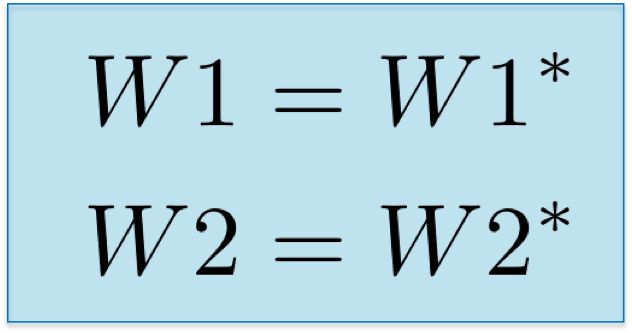
(ii) dLoss/dW1
Calculating the chain rule for updating the weights of the first hidden layer W1 shows the possibility of reusing existing calculations.
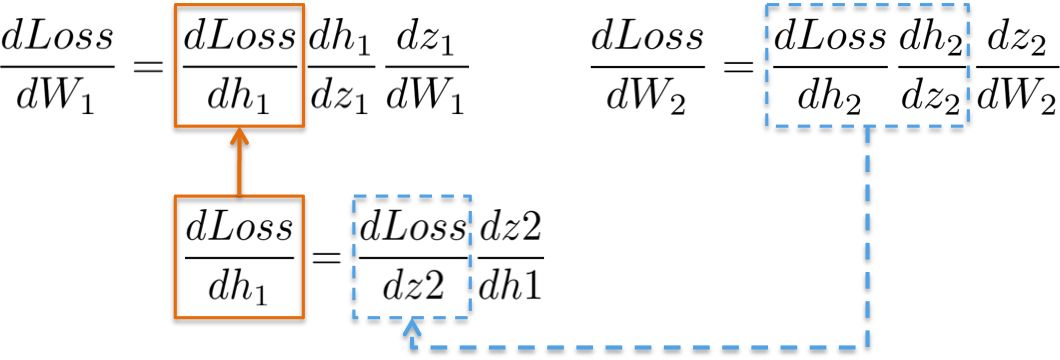
More intuitively, the path from the output layer to the weights W1 involves the partial derivatives that have already been computed in the previous layer.
For example, the partial derivatives dLoss/dh2 and dh2/dz2 have already been computed in the previous section as dependencies for the output layer dLoss/dW2 learning weights.
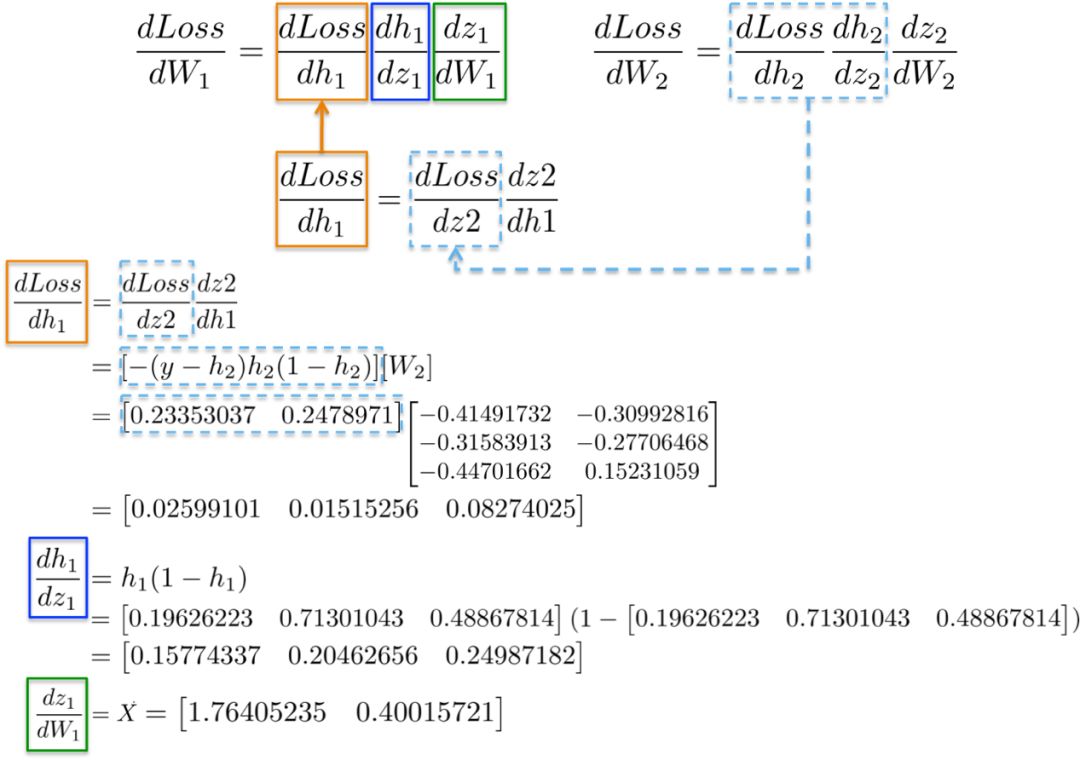
Putting all the derivatives together, we can again apply the chain rule to update the weights of the hidden layer W1:

Finally, we assign new weight values and complete the iteration of network training.
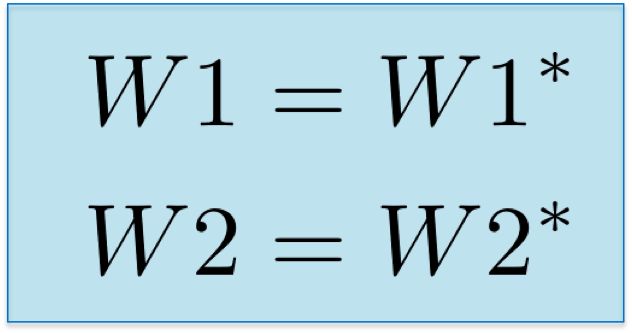
Implementation
Let’s convert the mathematical equations above into code using only Numpy as the linear algebra engine. The neural network is trained in a loop, where calibrated input data is provided to the network in each iteration. In this small example, we consider the entire dataset in each iteration. Since we update the trainable parameters (the matrices w1 and w2 in the code) with the corresponding gradients (matrices dL_dw1 and dL_dw2) in each loop, the calculations for forward propagation, loss function, and backpropagation have good generalization. The code is in this repository:https://github.com/omar-florez/scratch_mlp

Let’s Run This!
The following are some trained neural networks that can approximate the XOR function over multiple iterations.
Left: Accuracy. Center: Learned decision boundary. Right: Loss function.
First, let’s see how the neural network with 3 neurons in the hidden layer has small capacity. The model learns to separate the two classes with a simple decision boundary that starts as a straight line and then shows nonlinear behavior. As training continues, the loss function decreases well in the correct case.
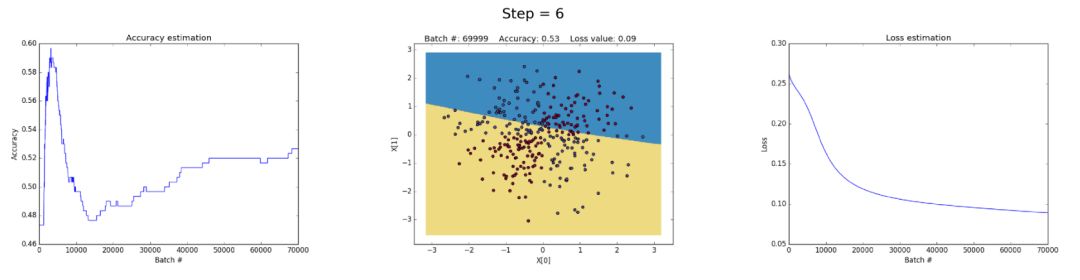
Having 50 neurons in the hidden layer significantly enhances the model’s ability to learn more complex decision boundaries. This not only produces more accurate results but also utilizes the gradients, which is a notable issue when training neural networks. This occurs when very large gradients multiply the weights during backpropagation, resulting in larger weight updates. This is why the loss value suddenly increases in the last step (step > 90). The regularization part of the loss function, which computes the squared values of the weights (sum(W²)/2N), has already become very large.
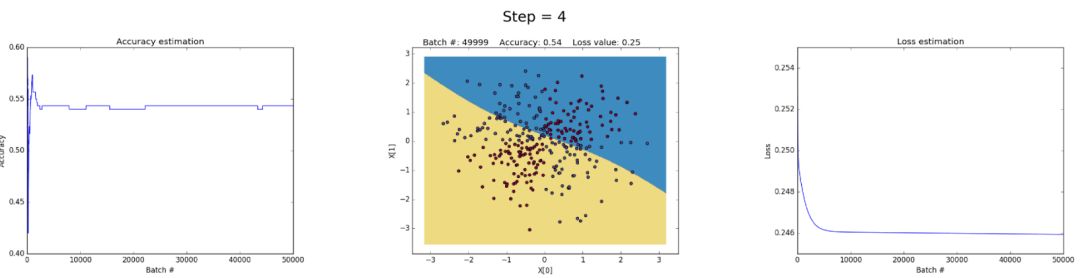
This problem can be avoided by lowering the learning rate, as shown below. Or by implementing a policy that decreases the learning rate over time. Or by strengthening regularization, perhaps using L1 instead of L2. Explaining gradients and the gradient vanishing is an interesting phenomenon that we will analyze in detail later.

Steps to run the code:
git clone:https://github.com/omar-florez/
scratch_mlp/python scratch_mlp / scratch_mlp.py
