
This article is about 3200 words long and suggests a reading time of 6 minutes.
Graph Neural Networks (GNN) are a type of deep learning method particularly adept at handling data with a graph structure.
Graph Neural Networks (GNN) are a type of deep learning method particularly good at handling data with a graph structure. Through specific strategies involving nodes and edges, GNN can transform graph data into a standard format that neural networks can train on. GNN performs exceptionally well in tasks such as node classification, edge information propagation, and graph clustering.
Compared to other graph learning algorithms, GNN exhibits outstanding learning capabilities, adept at uncovering the deep-seated patterns and semantic features hidden behind nodes and edges in graph data. With this powerful ability, GNN can make more accurate predictions and yield more stable results in various domains.
1 Overview of Graph Neural Network Models
1.1 Graph Convolutional Networks
Convolutional Neural Networks (CNN) perform well in fields like image recognition and natural language processing, but they can only handle regular data, such as grids and sequences. When faced with irregular data, such as social media network data, chemical structure data, biological protein data, or knowledge graph data, CNN falls short. Therefore, to address this issue, researchers attempted to extend CNN to graph-structured data, resulting in Graph Convolutional Networks (GCN). GCN is an important component of Graph Neural Networks (GNN), laying the groundwork for many subsequent models. Below, we will briefly discuss GCN from three aspects: spectral methods, spatial methods, and pooling.
Graph Convolutional Networks Based on Spectral Methods
Spectral method graph convolutional networks are a special type of neural network that utilizes spectral theory from graph signal processing to define convolution operations. It may sound complex, but it is akin to transforming graph signals into frequency domain signals and then defining convolution operations on these signals. This is similar to adjusting the volume on a music spectrum and then playing music on the adjusted spectrum. The benefit of this approach is its ability to handle irregular graph-structured data effectively, while also being flexibly applicable in various scenarios.
Spectral method graph convolutional networks have been employed in many fields, such as image recognition, natural language processing, and social network analysis. They are like a Swiss Army knife, useful in a variety of situations.
Table 1 provides a comprehensive summary of spectral method graph convolutional models, including aspects such as model, core ideas, types of graphs, learning modes, activation functions, data, and tasks. If you wish to delve deeper into this neural network, this table can provide you with a wealth of useful information.

Graph Convolutional Networks Based on Spatial Methods
Spatial method graph convolutional networks are a model of graph neural networks, primarily tasked with classifying graphs or classifying nodes within graphs. This method differs from the previously mentioned spectral method graph convolutional networks, as it does not operate based on signal processing theory but directly performs convolution operations in the spatial domain.
How does this model achieve its goals? It transforms graph data into a suitable format for processing, allowing the model to better handle graph data, thereby enhancing the performance of graph convolutional networks. Such networks can better capture spatial information in graph data, making the model smarter and more adaptable to new situations.
Figure 1 illustrates this processing flow. This model has significant utility in various fields, such as geographic information systems, social networks, and bioinformatics. With this model, we can better process and understand graph data in these fields, bringing more convenience and value to our lives and work.
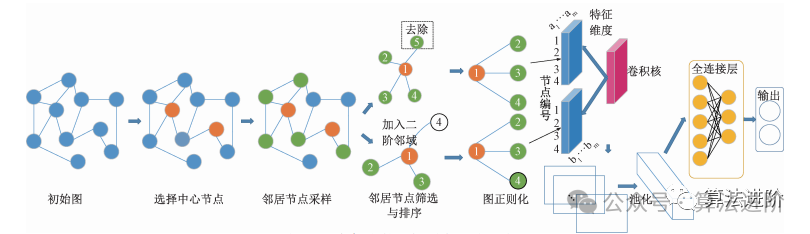
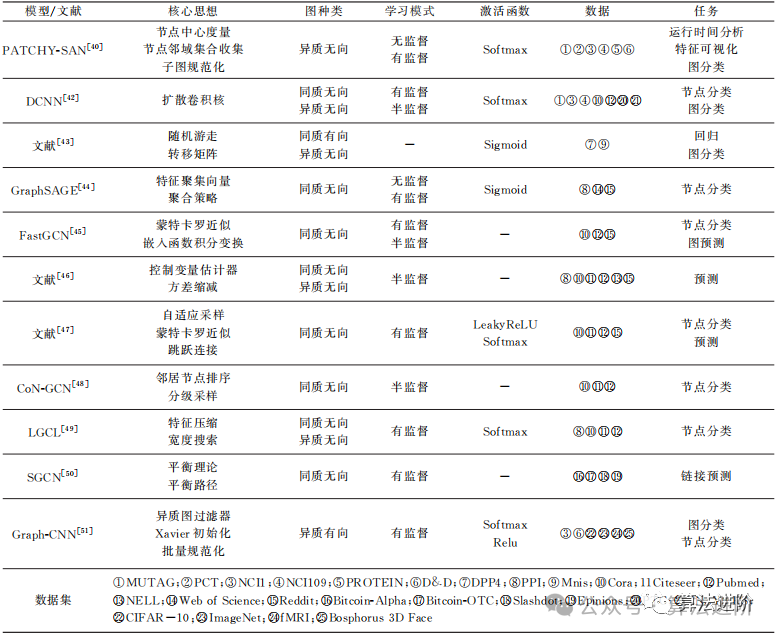
Table 2 summarizes the spatial method graph convolution models based on aspects such as model, core ideas, types of graphs, learning modes, activation functions, data, and tasks.
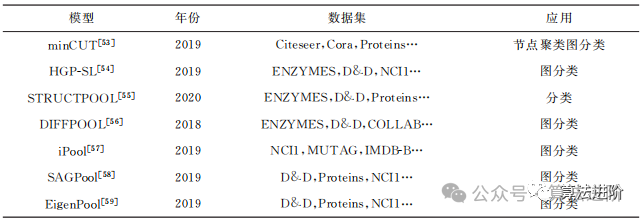
Pooling-Based Graph Convolutional Networks
In simple terms, the pooling-based graph convolutional network (Pooling-based GCN) reduces graph data size by adding a pooling layer, making computations faster and requiring less memory. Pooling operations can be global, local, or adaptive. Global pooling treats the entire graph as a whole, making it suitable for tasks like node classification, community detection, and link prediction. Local pooling divides the graph into smaller segments and processes each segment, making it suitable for community detection and node classification tasks. Adaptive pooling is smarter; it automatically selects areas to process based on the graph’s structure and features, thereby better preserving the graph’s structure and feature information. Finally, Table 3 summarizes these pooling-based graph convolutional network models clearly and concisely.
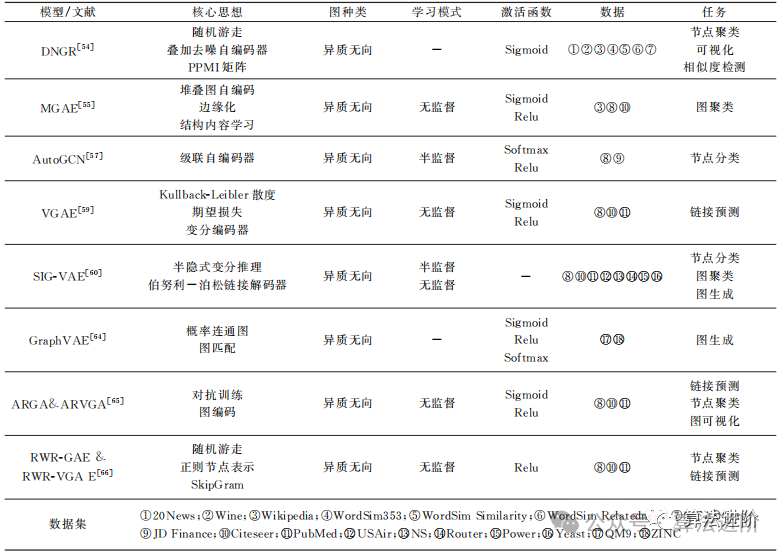
1.2 Graph Autoencoders
Combining autoencoders with graph neural networks is like merging two powerful tools into one. This allows for better learning and understanding of graph-structured data. Graph autoencoders consist of two parts: an encoder and a decoder, much like taking a photo with your phone and then viewing it. Through this process, it learns hidden patterns and structural information from unlabeled graph-structured data and preserves it in a simple way. The graph neural network then utilizes this straightforward information, acting like a “supervisor” to learn, enabling better classification and prediction of graph-structured data. Compared to previous methods, this approach is stronger and more accurate, making it useful in various fields, such as recommendation systems, social network analysis, and bioinformatics.
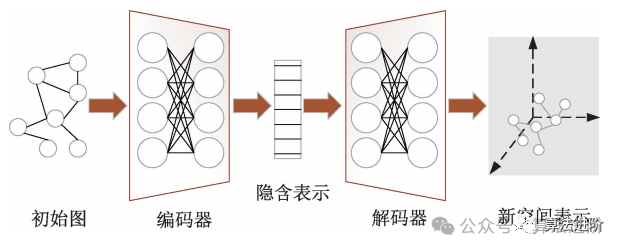
Table 4 summarizes the graph autoencoder models based on aspects such as model, core ideas, types of graphs, learning modes, activation functions, data, and tasks.
1.3 Graph Generative Networks
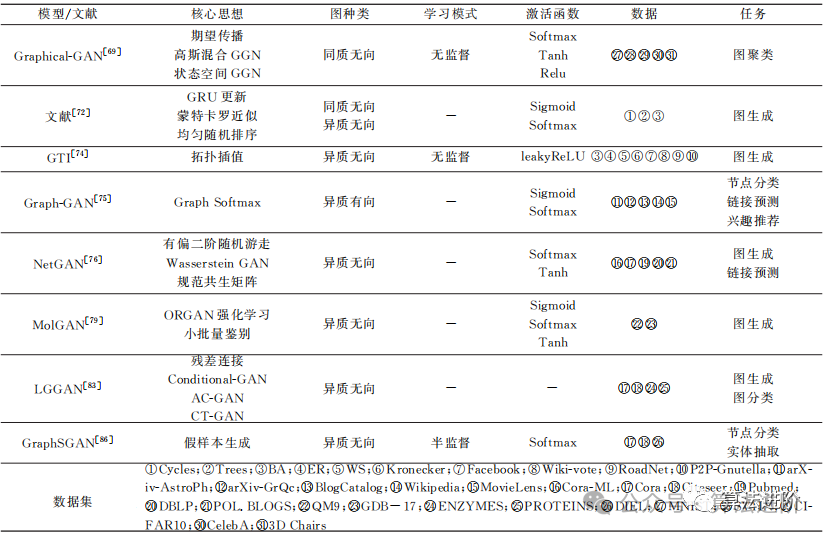
Graph generative networks generate graph data with specific attributes and requirements by recombining nodes and edges according to certain rules. However, simulating complex distributions and sampling from them is not an easy task. Some graph data is unique, high-dimensional, and exhibits complex non-local dependencies between edges. Therefore, we cannot assume that all graph data comes from the same source, especially for special graphs, where the model must adapt to various changes during recognition.
The input to a graph generative network can be vectors of nodes or edges, or already given graph embedding representations. It learns from sampled data to synthesize the graph required for various tasks. This model is useful in many fields, such as predicting the structure of chemical molecules, analyzing social networks, and constructing knowledge graphs. In summary, graph generative networks are powerful tools that help us better understand and handle graph data.
Table 5 summarizes the graph generative network models based on aspects such as model, core ideas, types of graphs, learning modes, activation functions, data, and tasks.
1.4 Graph Recurrent Networks
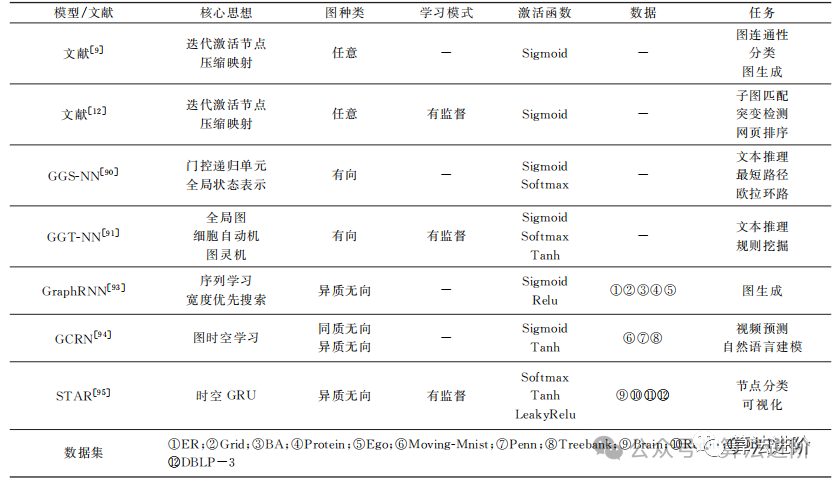
Graph recurrent networks are based on familiar recurrent neural networks, specifically designed to handle graph-structured data. Unlike traditional recurrent neural networks, graph recurrent networks consider the connection relationships between nodes, allowing them to better process data within graph structures.
In graph recurrent networks, each node has its own state, and they communicate with neighboring nodes to update their states. This network structure is truly remarkable, as it can better identify relationships between nodes, regardless of the type of graph structure, whether it be heterogeneous or directed.
Graph recurrent networks are highly practical, applicable in many fields, such as social networks and protein interaction networks in bioinformatics. In summary, graph recurrent networks are powerful tools for processing graph-structured data, simplifying and enhancing our data processing.
Table 6 summarizes the graph recurrent network models based on aspects such as model, core ideas, types of graphs, learning modes, activation functions, data, and tasks.
1.5 Graph Attention Networks
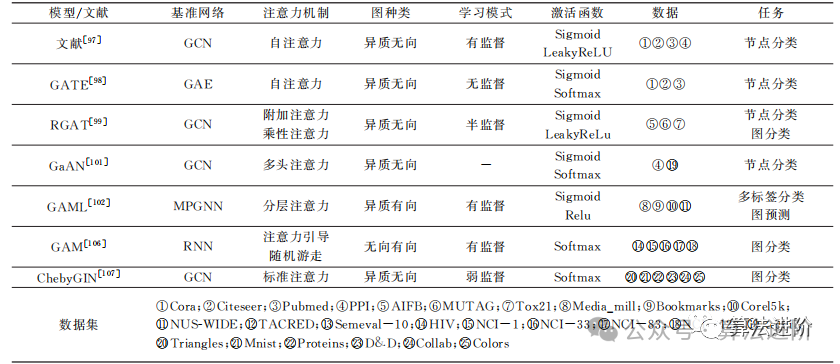
Graph Attention Networks (GAT) are a new neural network structure that helps us better process data that resembles graphs. Traditional neural networks may struggle with such data, but GAT allows each node to have different weights in relation to its neighboring nodes, emphasizing important connections.
How are these weights determined? They are based on the inner product of node features. The size of the inner product indicates the importance of the relationship between nodes. Thus, GAT can learn the importance of relationships between different nodes and integrate information accordingly.
GAT also introduces attention mechanisms and multi-head attention mechanisms, enabling it to better handle graph-structured data. Therefore, GAT has broad application prospects in various fields, such as social network analysis, recommendation systems, and bioinformatics.
Table 7 summarizes the graph attention network models based on aspects such as model, core ideas, types of graphs, learning modes, activation functions, data, and tasks.
2 Comparison of Graph Neural Network Models
Graph Neural Networks can be broadly categorized into five types: Graph Convolutional Networks, Graph Autoencoders, Graph Generative Networks, Graph Recurrent Networks, and Graph Attention Networks. Each type has its own algorithms and applicable areas, but they are not mutually exclusive. In practical applications, we should select the most suitable graph neural network based on the distribution of the graph, feature information, and task requirements to effectively learn graph-structured data. Table 8 summarizes the principles, advantages, disadvantages, applicable scopes, and implementation costs of various GNN models.
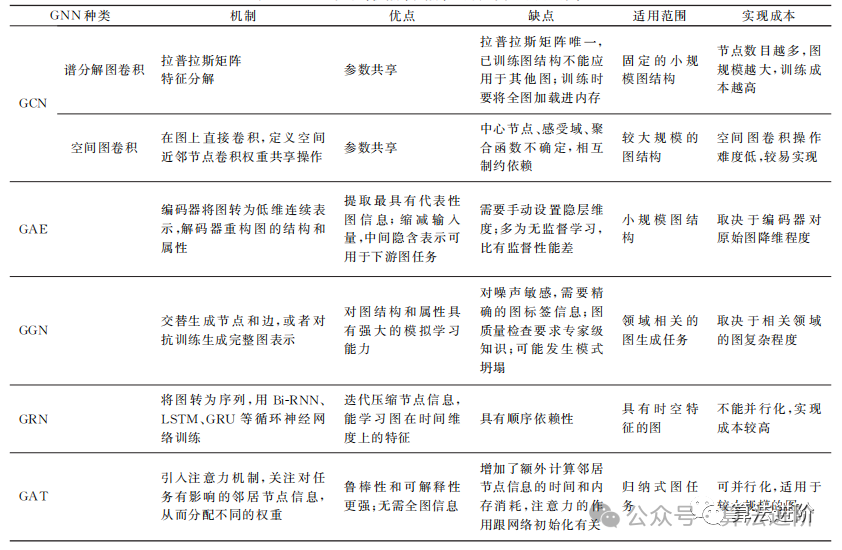
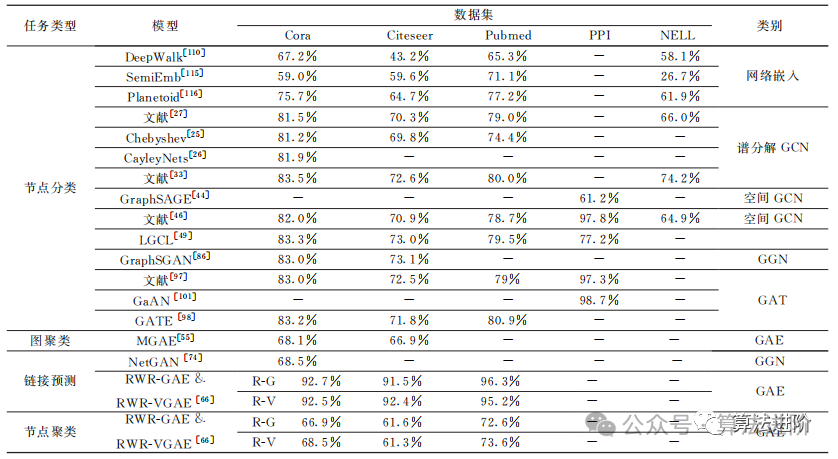
Table 9 presents the experimental data of major GNN algorithms, including three citation network datasets: Cora, Citeseer, and Pubmed, as well as the protein dataset PPI and the knowledge graph dataset NELL. It compares four benchmark tasks: node classification, graph clustering, link prediction, and node clustering.
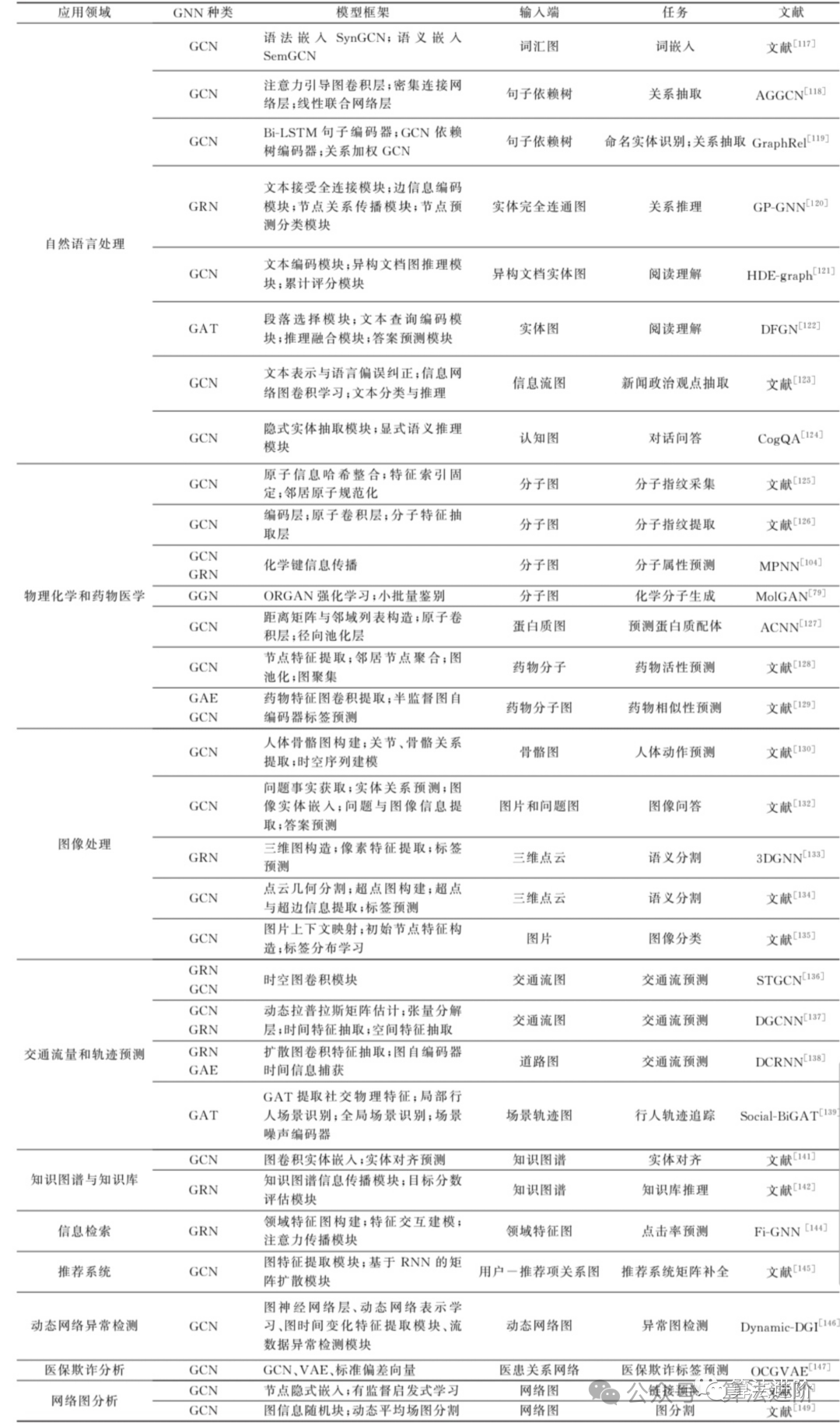
3 Applications
GNN can effectively learn the features of graph-structured data, making it applicable in many graph-related areas. Specifically, it excels in natural language processing, physical chemistry and pharmacology, image processing, traffic flow and trajectory prediction, among others. Furthermore, it plays a crucial role in other areas such as knowledge graphs, information retrieval, dynamic network anomaly detection, healthcare fraud analysis, and network graph analysis. You can refer to Table 10 for more examples of GNN applications.
Editor: Yu Tengkai
Proofreader: Lin Yilin

