Neural networks are the backbone of deep learning, and among the various neural network models, RNNs are the most classic. Despite their imperfections, they possess the ability to learn from historical information. Subsequent frameworks, whether the encode-decode framework, attention models, self-attention models, or the more powerful Bert model family, have evolved and strengthened by standing on the shoulders of RNNs.
This article elaborates on all aspects of RNNs, including model structure, advantages and disadvantages, various applications of RNN models, commonly used activation functions, the shortcomings of RNNs, and how GRU and LSTM attempt to address these issues, along with RNN variants.
The standout feature of this article is its illustrated version, followed by concise language and comprehensive summaries.
Overview
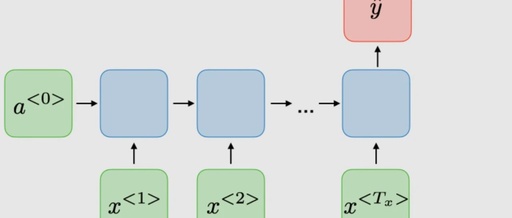
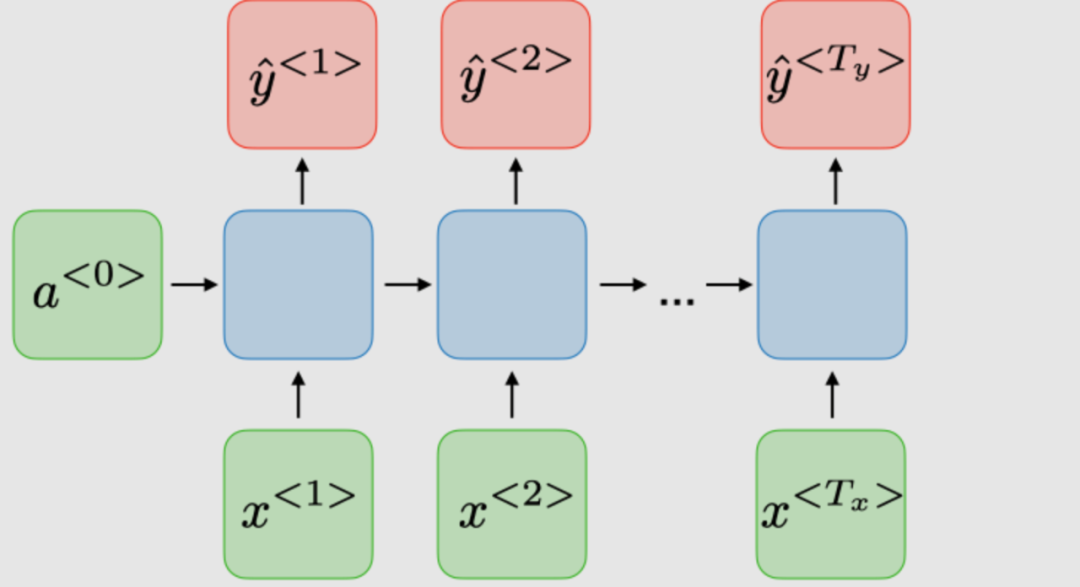
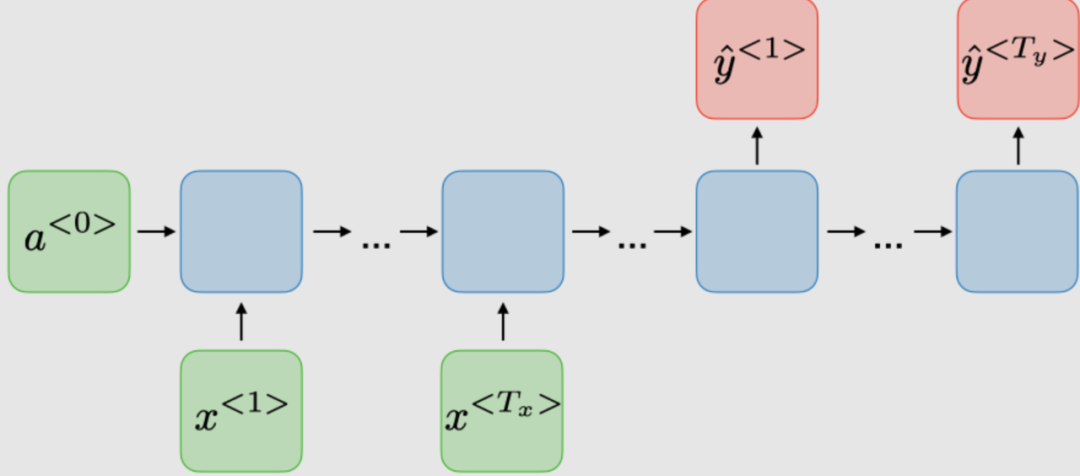
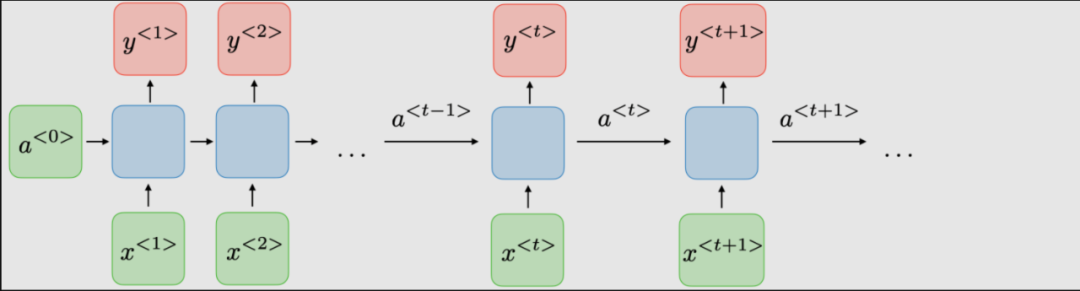
The traditional architecture of RNNs. Recurrent neural networks, also known as RNNs, are a class of neural networks that allow previous outputs to be used as inputs while maintaining hidden states. They are typically depicted as follows:
For each time step, the activation function and output are expressed as:
Here, the shared weight coefficient of the time dimension network is:
is the activation function
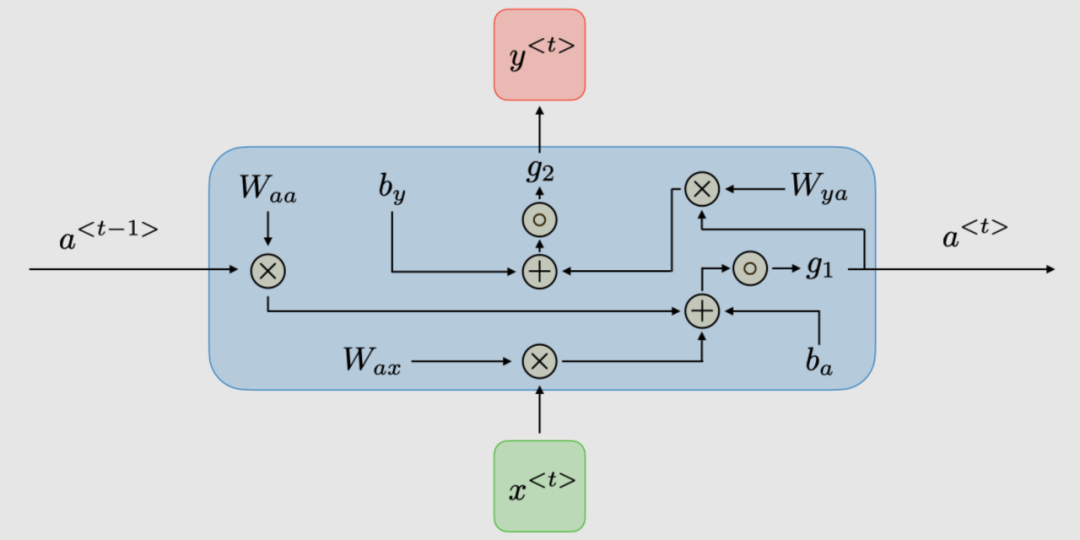
The table below summarizes the advantages and disadvantages of typical RNN architectures:
| Advantages | Disadvantages |
|---|---|
| Handles input of arbitrary length | Slow computation speed |
| Model shape does not change with increasing input length | Hard to retrieve information from a long time ago |
| Computationally considers historical information | Cannot consider any future inputs for the current state |
| Weights are shared over time |
Applications of RNNs
RNN models are primarily applied in the fields of natural language processing and speech recognition. The table below summarizes different applications:
| RNN Type | Illustration | Examples |
|---|---|---|
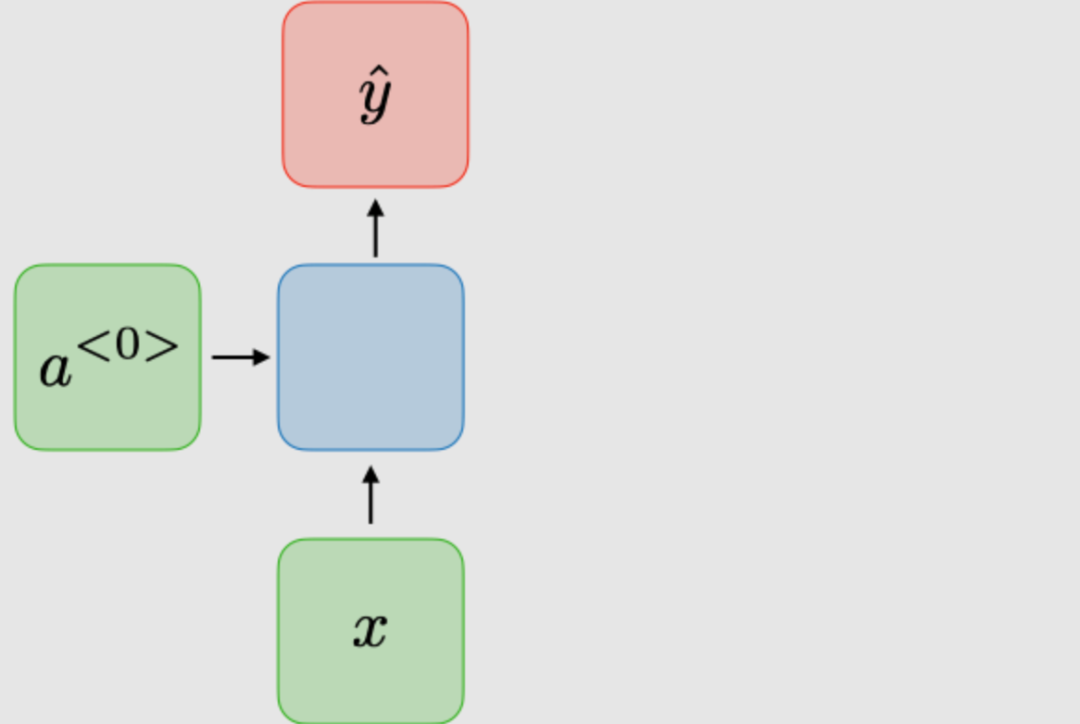
| 1-to-1 |
|
Traditional neural network |
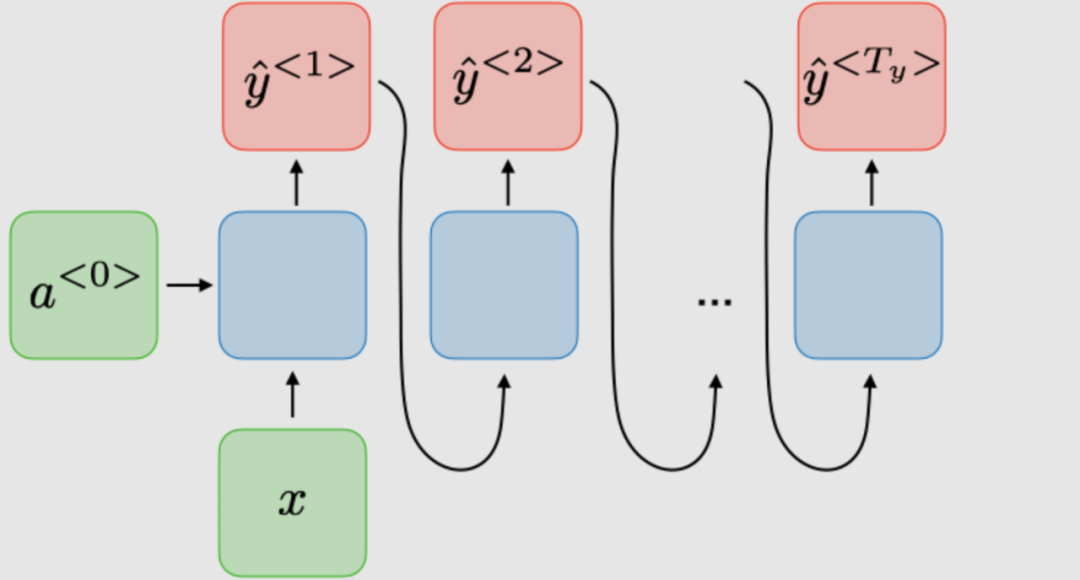
| 1-to-many |
|
Music generation |
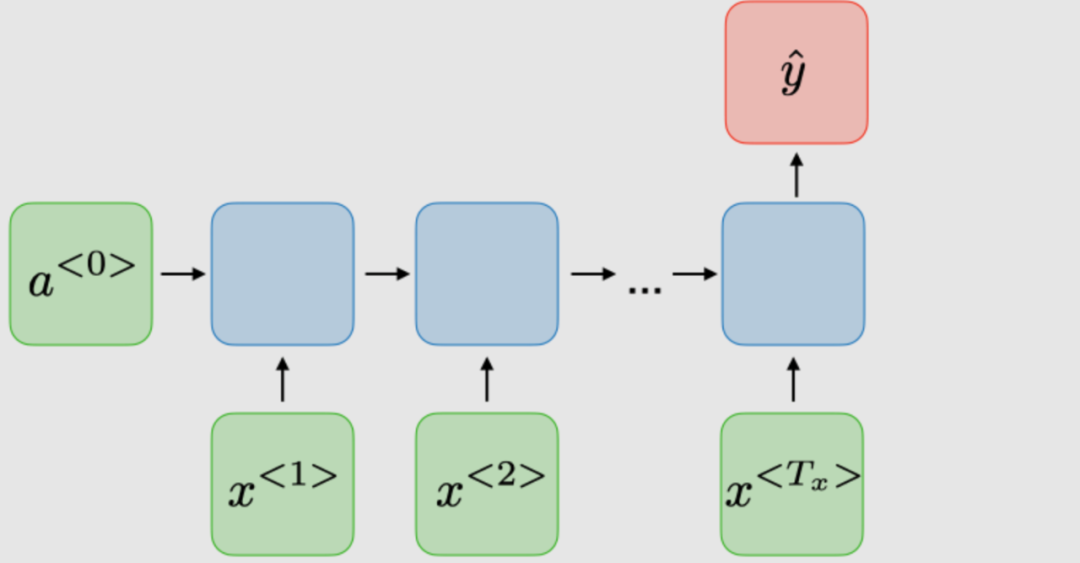
| Many-to-1 |
|
Sentiment classification |
| Many-to-many |
|
Named entity recognition |
| Many-to-many |
|
Machine translation |
Loss Function
For RNN networks, the loss function across all time steps is defined based on the loss at each time step as follows:
Backpropagation Through Time
Backpropagation is performed at each time point. At time step, the partial derivative of the loss with respect to the weight matrix is represented as follows:
Handling Long-Short Dependencies
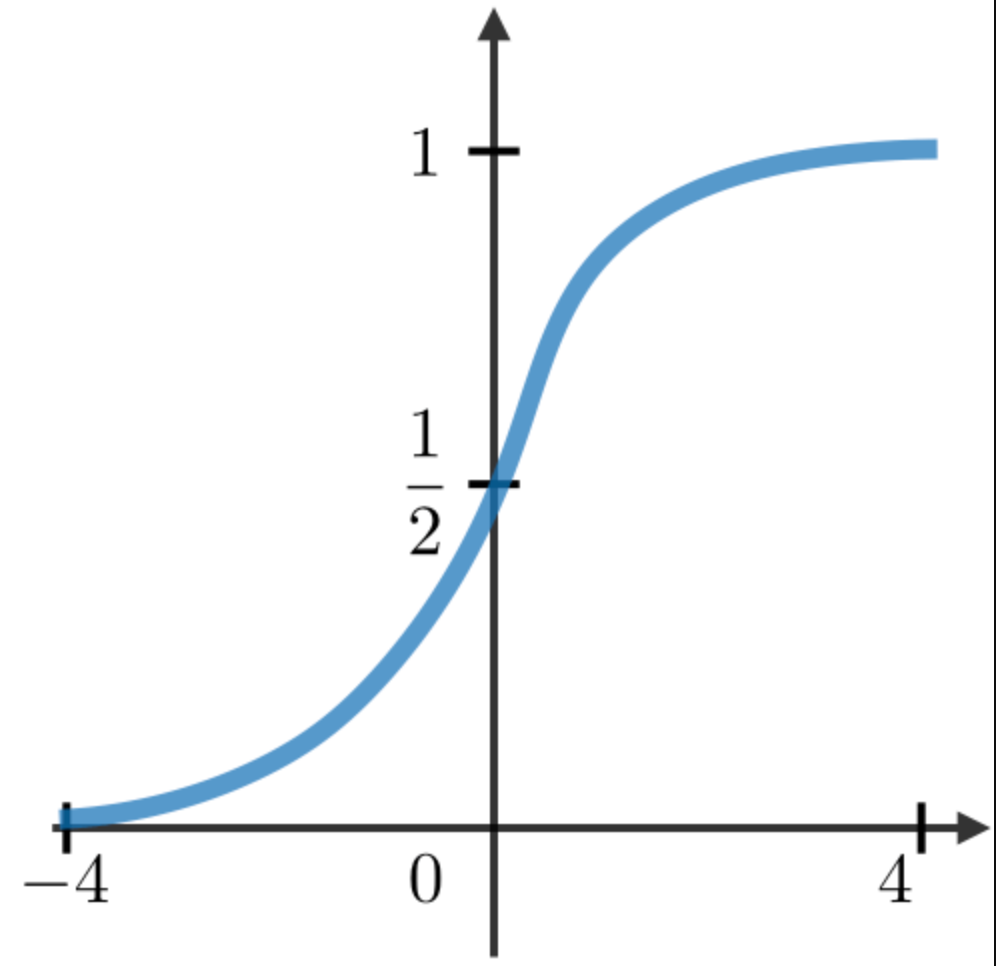
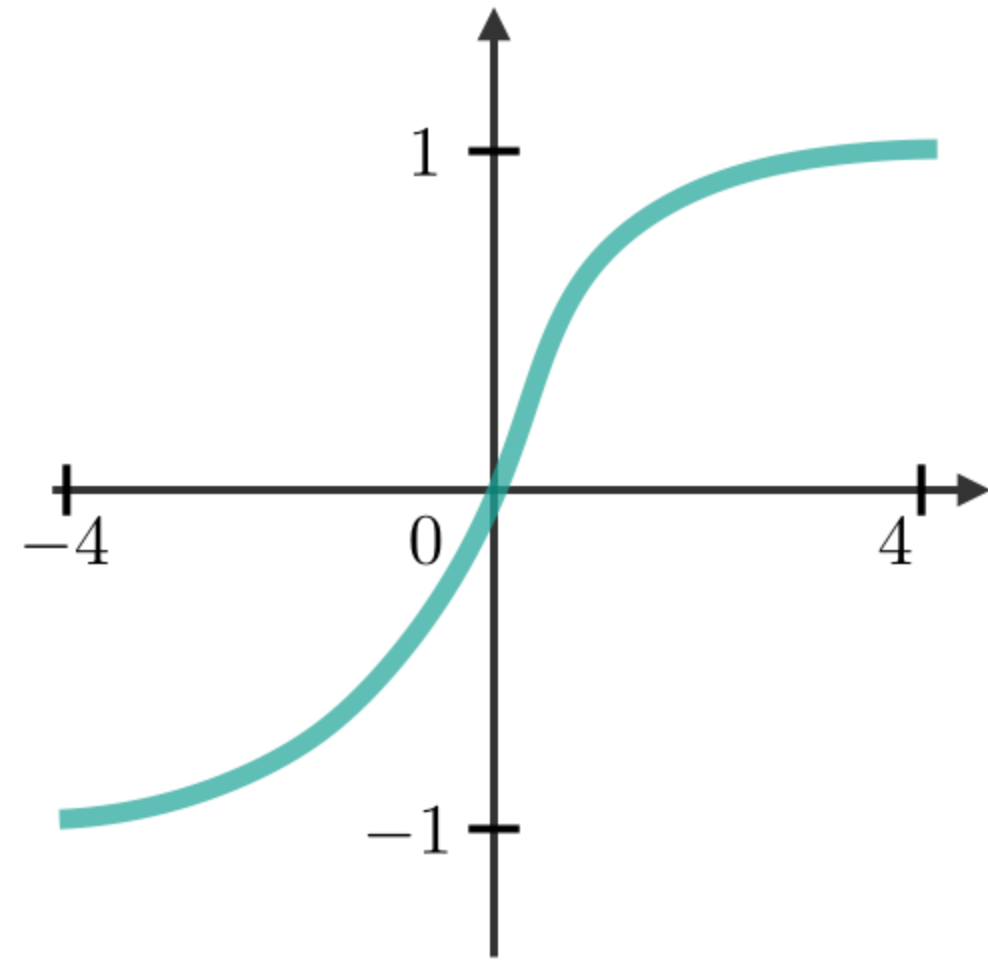
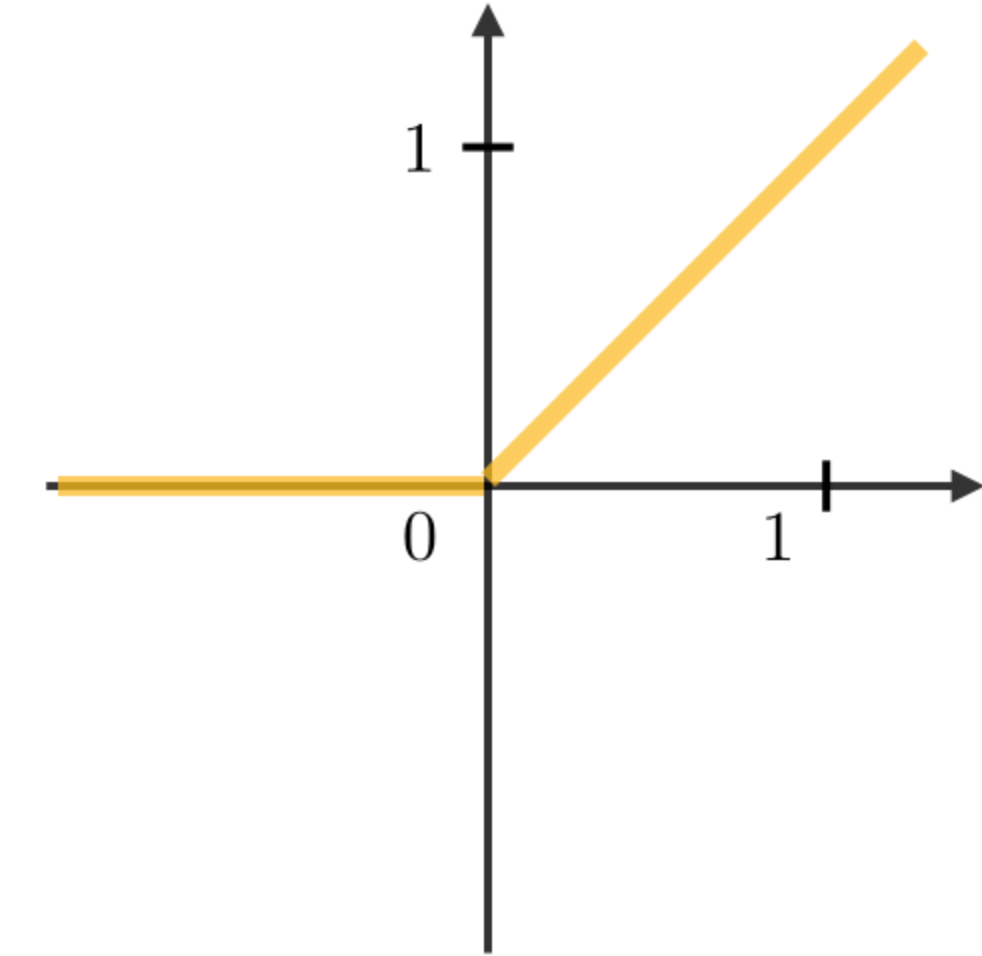
Commonly Used Activation Functions
The most commonly used activation functions in RNN modules are described as follows:
| Sigmoid | Tanh | RELU |
|---|---|---|
|
|
|
|
Gradient Vanishing/Exploding
In RNNs, the vanishing and exploding gradient phenomena are often encountered. This occurs because it is difficult to capture long-term dependencies, as the multiplicative gradients can decrease/increase exponentially with the number of layers.
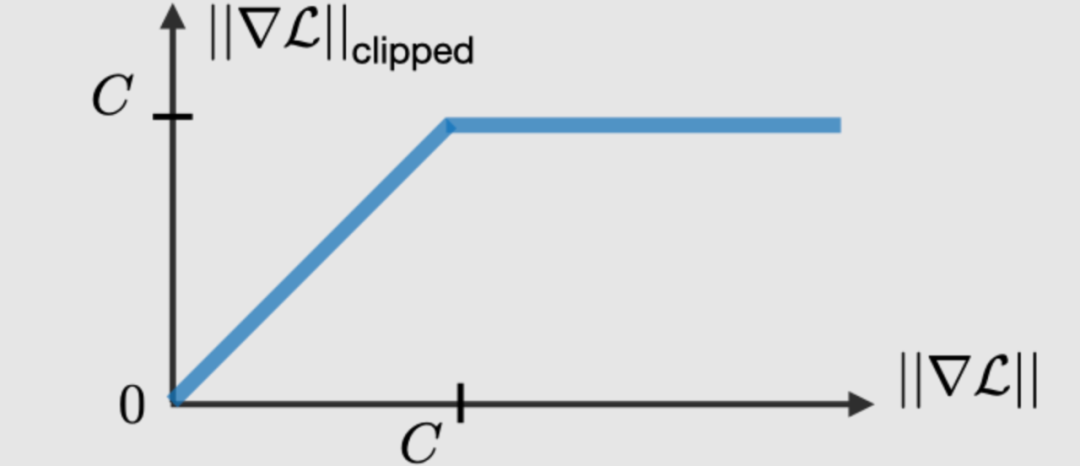
Gradient Clipping
Gradient clipping is a technique used to control the gradient explosion problem sometimes encountered during backpropagation. By limiting the maximum value of the gradient, this phenomenon is managed in practice.
Types of Gates
To address the vanishing gradient problem, specific gates are used in certain types of RNNs, and they usually have a clear purpose. They are commonly labeled as follows:
Where, are gate-specific coefficients, and are sigmoid functions. The main content is summarized in the table below:
| Type of Gate | Function | Application |
|---|---|---|
| Update Gate | How important is the past to the present? | GRU, LSTM |
| Reset Gate | Discard past information? | GRU, LSTM |
| Forget Gate | Is it erasing a unit? | LSTM |
| Output Gate | How much of the gate is exposed? | LSTM |
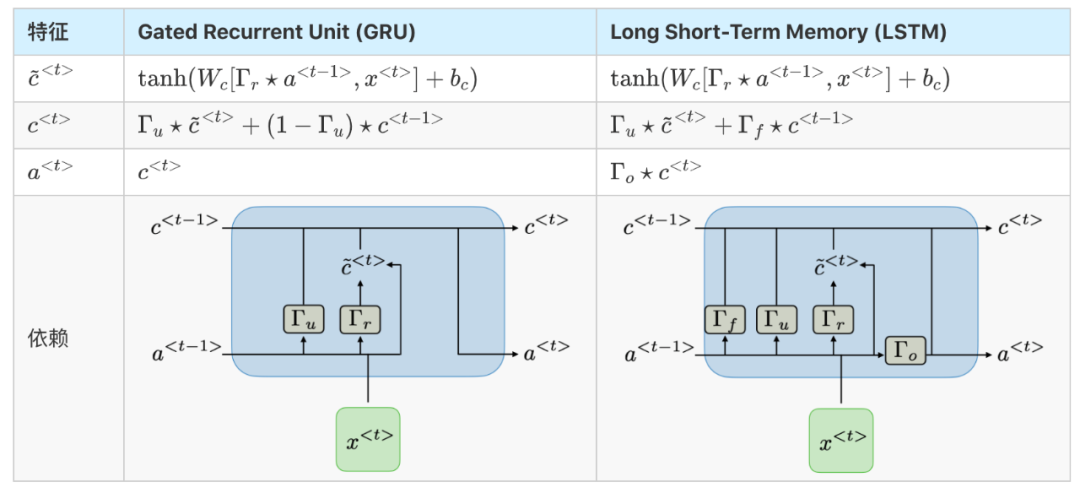
GRU/LSTM
Gated Recurrent Unit (GRU) and Long Short-Term Memory (LSTM) address the vanishing gradient problem encountered in traditional RNNs, with LSTM being an extension of GRU. The table below summarizes the characteristic equations of each structure:
Variants of RNNs
The table below summarizes other commonly used RNN models:
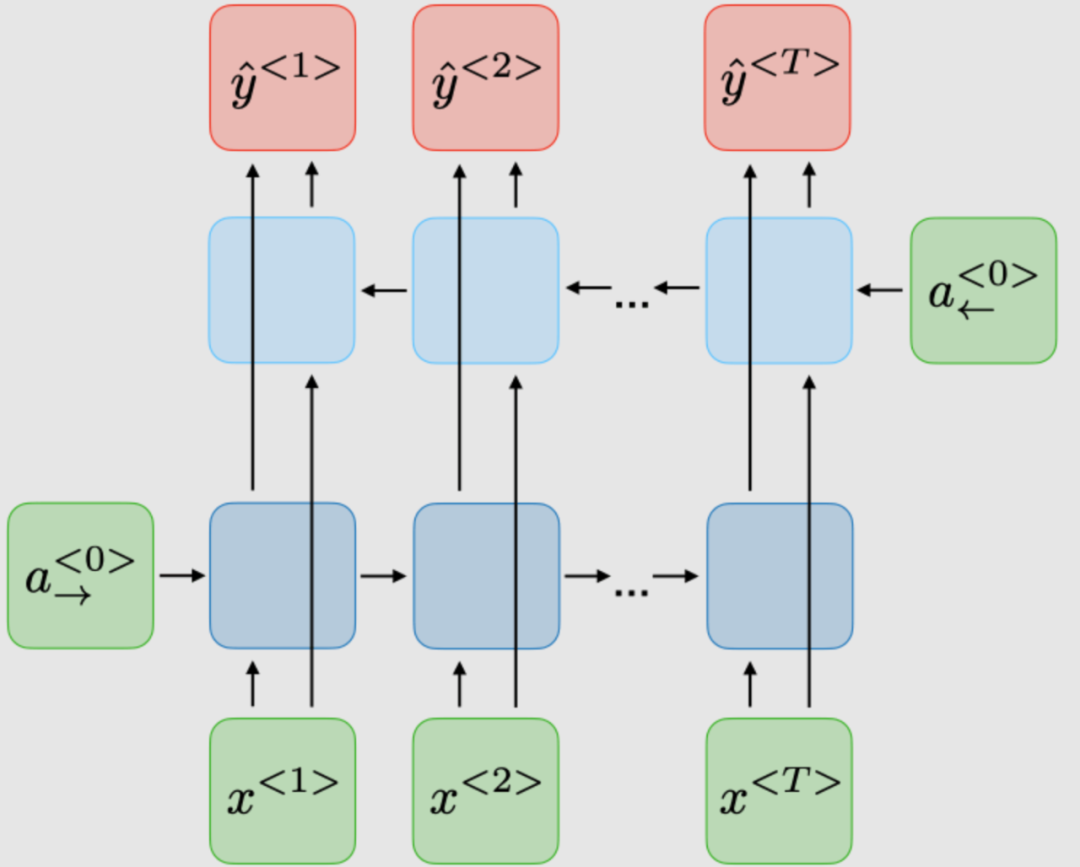
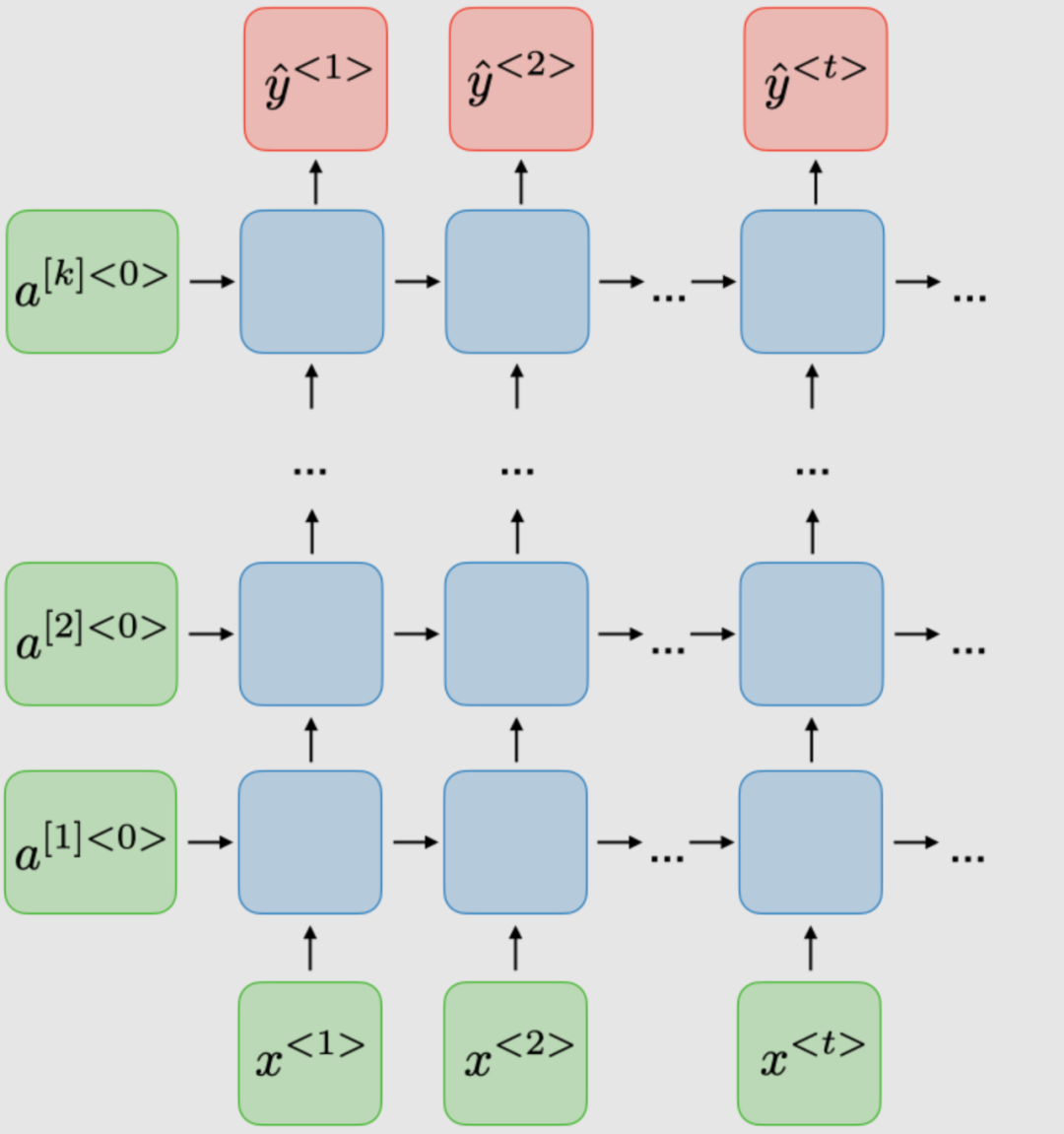
| Bidirectional (BRNN) | Deep (DRNN) |
|---|---|
|
|
|
References:
https://stanford.edu/~shervine/teaching/cs-230/cheatsheet-recurrent-neural-networks