Madio.net
Mathematics China
/// Editor: Yu Dizongxuan
This article is reprinted from the Mathematics Algorithm Club
The distinction between statistics and machine learning has always been vague.Both in industry and academia, it has been widely believed that machine learning is just a shiny facade over statistics.Moreover, artificial intelligence, supported by machine learning, is also referred to as the “extension of statistics.” For example, Nobel laureate Thomas Sargent once said that artificial intelligence is actually statistics, just with a more glamorous vocabulary.
Sargent stated at the World Science and Technology Innovation Forum that artificial intelligence is essentially statistics.Of course, there are some differing opinions. However, the arguments from both sides of this viewpoint are filled with seemingly profound yet actually ambiguous discussions, making it quite confusing.A Harvard doctoral student named Matthew Stewart has argued from two perspectives: the differences between statistics and machine learning, and the differences between statistical models and machine learning, demonstrating that machine learning and statistics are not interchangeable terms.The main difference between machine learning and statistics lies in their objectives.
Contrary to what most people think, machine learning has actually existed for decades. Initially, it was gradually abandoned because the computing power at that time could not meet its demand for massive calculations. However, in recent years, due to the data and computational advantages brought by information explosion, machine learning is rapidly reviving.To get back on track, if machine learning and statistics were interchangeable terms, why haven’t we seen every university’s statistics department shut down and switch to a ‘machine learning’ department? Because they are different!I often hear vague discussions on this topic, the most common being: “The main difference between machine learning and statistics lies in their objectives. Machine learning models aim to make the most accurate predictions possible. Statistical models are designed to infer the relationships between variables.”While this is technically correct, such statements do not provide a particularly clear or satisfactory answer. One major difference between machine learning and statistics is indeed their objectives.However, saying that machine learning is about accurate predictions while statistical models are designed for inference is almost meaningless unless you are truly proficient in these concepts.
First, we must understand that statistics and statistical modeling are not the same. Statistics is the mathematical study of data. Without data, statistics cannot be conducted. Statistical models are models of data, primarily used to infer the relationships between different contents in the data, or to create models that can predict future values. Usually, these two are complementary.Therefore, we actually need to discuss from two aspects: first, what are the differences between statistics and machine learning; second, what are the differences between statistical models and machine learning?To put it more bluntly, there are many statistical models that can make predictions, but the predictive performance is often disappointing.On the other hand, machine learning often sacrifices interpretability for powerful predictive capabilities. For example, from linear regression to neural networks, although interpretability decreases, predictive power significantly increases.From a macro perspective, this is a good answer. At least for most people, it is good enough. However, in some cases, this statement can easily lead us to misunderstand the differences between machine learning and statistical modeling. Let’s take a look at the example of linear regression.The Differences Between Statistical Models and Machine Learning in Linear Regression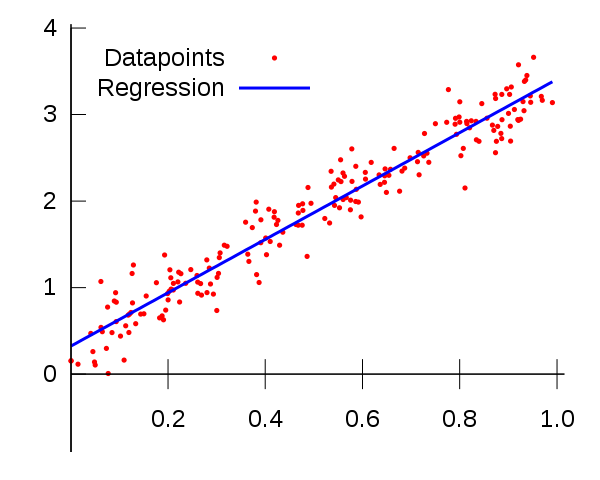
Perhaps it is the similarity in methods used in statistical modeling and machine learning that leads people to believe they are the same thing. I can understand this, but in fact, it is not the case.The most obvious example is linear regression, which may be the primary cause of this misunderstanding. Linear regression is a statistical method through which we can both train a linear regressor and fit a statistical regression model using the least squares method.As we can see, in this case, the former is called “training” the model, which only uses a subset of the data, and the performance of the trained model needs to be tested on another subset, the test set, to determine how it performs. In this example, the ultimate goal of machine learning is to achieve the best performance on the test set.For the latter, we assume in advance that the data is a linear regression quantity with Gaussian noise, and then we try to find a line that minimizes the mean square error of all data. No training or test set is needed; in many cases, especially in research (such as the sensor example below), the purpose of modeling is to describe the relationship between data and output variables, rather than to predict future data. We call this process statistical inference, rather than prediction. Although we can use this model for prediction, which might be what you think, the method of evaluating the model is no longer the test set but rather the significance and robustness of the model parameters.Machine learning (specifically referring to supervised learning) aims to obtain a model that can make repeatable predictions. We generally do not care whether the model is interpretable. Machine learning only cares about the results. It is like, for a company, your value is only measured by your performance. On the other hand, statistical modeling is more about finding relationships between variables and determining the significance of those relationships, which coincidentally aligns with prediction.Let me give an example to illustrate the differences between the two. I am an environmental scientist. My main job involves dealing with sensor data. If I try to prove that a sensor can respond to a certain stimulus (such as gas concentration), I will use a statistical model to determine whether the signal response is statistically significant. I will attempt to understand this relationship and test its repeatability so that I can accurately describe the sensor’s response and make inferences based on this data. I may also test whether the response is linear? Is the response attributed to gas concentration rather than random noise in the sensor? And so on.At the same time, I can also take data from 20 different sensors and try to predict a sensor’s response that can be characterized by them. If you are not familiar with sensors, this may seem a bit strange, but this is indeed an important research area in environmental science.Using a model with 20 different variables to characterize the output of a sensor is clearly a prediction, and I do not expect the model to be interpretable. It is worth noting that due to factors such as nonlinearity caused by chemical kinetics and the relationship between physical variables and gas concentrations, this model may become very obscure, just like a neural network that is difficult to interpret. Although I hope this model is understandable, I would be quite happy as long as it can make accurate predictions.If I try to prove that the relationships between data variables are statistically significant to some extent so that I can publish in a scientific paper, I will use a statistical model rather than machine learning. This is because I am more concerned with the relationships between variables rather than making predictions. Making predictions may still be important, but most machine learning algorithms lack interpretability, which makes it difficult to prove the relationships that exist in the data.
Clearly, these two approaches differ in their objectives, even though they use similar methods to achieve their goals. The evaluation of machine learning algorithms uses a test set to verify their accuracy. However, for statistical models, analyzing regression parameters through confidence intervals, significance tests, and other tests can be used to assess the validity of the model. Because these methods yield similar results, it is easy to understand why people might assume they are the same.The Differences Between Statistics and Machine Learning in Linear RegressionThere is a misunderstanding that has persisted for a decade: it is unreasonable to confuse these two terms solely based on the fact that they both utilize the same basic probability concepts.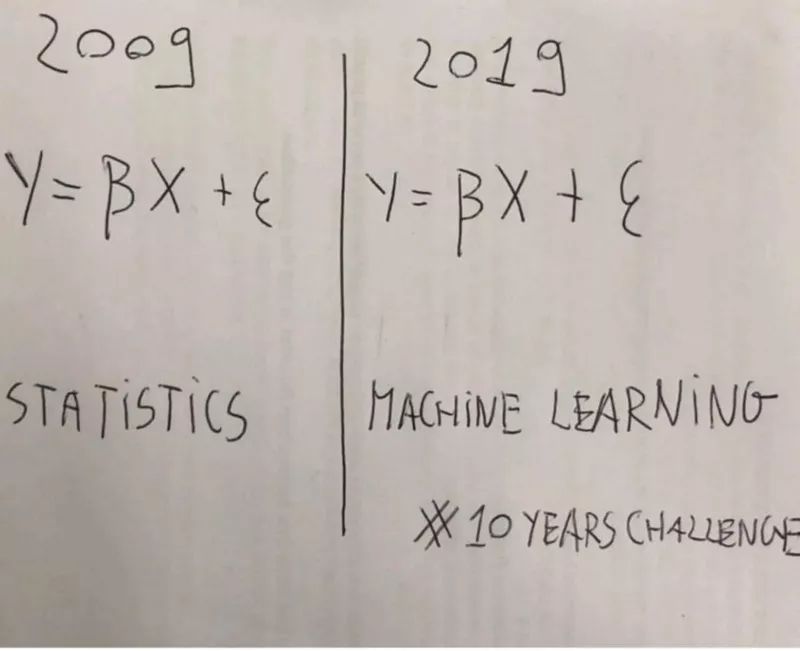
However, it is unreasonable to equate these two terms solely based on the fact that they both utilize the same basic probability concepts. It is like saying that if we merely consider machine learning as a shiny facade over statistics, we could also say:
- Physics is just a nicer way of saying mathematics.
- Zoology is just a nicer way of saying stamp collecting.
- Architecture is just a nicer way of saying sandcastle building.
These statements (especially the last one) are absurd and completely confuse the terminology of two similar ideas.In reality, physics is built on a mathematical foundation, and understanding physical phenomena in reality is the application of mathematics. Physics also encompasses various aspects of statistics, while modern statistics is often constructed within the framework of Zermelo-Frankel set theory combined with measure theory to produce probability spaces. They have much in common because they come from similar origins and apply similar ideas to reach a logical conclusion. Similarly, architecture and sandcastle building may have many similarities, but even if I am not an architect, I cannot provide a clear explanation, yet it is evident that they are clearly different.Before we proceed further, it is necessary to briefly clarify two other common misconceptions related to machine learning and statistics. That is, artificial intelligence is different from machine learning, and data science is different from statistics. These are uncontroversial issues, so they can be clarified quickly.Data science essentially involves computational and statistical methods applied to data, including small datasets or large datasets. It also includes things like exploratory data analysis, which involves checking and visualizing data to help scientists better understand the data and make inferences from it. Data science also includes things like data wrapping and preprocessing, thus involving a certain degree of computer science, as it involves coding and establishing connections between databases, web servers, and pipelines, etc.To conduct statistics, you do not necessarily have to rely on a computer, but if it is data science, it cannot operate without a computer. This again illustrates that although data science relies on statistics, the two are not the same concept.Similarly, machine learning is not artificial intelligence; in fact, machine learning is a branch of artificial intelligence. This is quite evident, as we “teach” (train) machines to make general predictions about specific types of data based on past data.Machine Learning Is Based on StatisticsBefore we discuss the differences between statistics and machine learning, let’s first talk about their similarities, which have already been explored in the first half of the article.Machine learning is based on a statistical framework because it involves data, and data must be described within a statistical framework, so this point is quite clear. However, extending to the statistical mechanisms for a large number of particles in thermodynamics is also built on a statistical framework.The concept of pressure is essentially data, and temperature is also a form of data. You might think this sounds unreasonable, but it is true. That is why you cannot describe the temperature or pressure of a molecule; it is unreasonable. Temperature is a display of the average energy produced by molecular collisions. For entities like houses or the outdoors that have a large number of molecules, it is reasonable for us to describe them using temperature.Would you consider thermodynamics and statistics to be the same thing? Certainly not; thermodynamics uses statistics to help us understand the interactions of motion and the heat generated in transfer phenomena.In fact, thermodynamics is based on multiple disciplines rather than just statistics. Similarly, machine learning is based on many other fields, such as mathematics and computer science. For example:
- The theories of machine learning originate from mathematics and statistics;
- Machine learning algorithms are based on optimization theory, matrix algebra, and calculus;
- The implementation of machine learning comes from concepts in computer science and engineering, such as kernel mapping, feature hashing, and so on.
When someone starts programming with Python and suddenly finds and uses these algorithms from the Sklearn library, many of the above concepts are quite abstract, making it difficult to see the distinctions within them. In such cases, this abstract definition leads to a certain degree of ignorance about what machine learning truly encompasses.Statistical Learning Theory – The Statistical Foundation of Machine LearningThe main difference between statistics and machine learning is that statistics is entirely based on probability spaces. You can derive all of statistical content from set theory, which discusses how we classify data (these classes are called “sets”) and then measure this set to ensure its total sum is 1. We call this method probability space.Statistics does not have any other assumptions beyond defining these sets and measurements. This is why we have a very rigorous definition of probability spaces. A probability space, mathematically denoted as (Ω,F,P), consists of three parts:
- A sample space, Ω, which is the set of all possible outcomes.
- A collection of events, F, where each event contains 0 or other values.
- Assigning probabilities to each event, P, which is a function mapping events to probabilities.
Machine learning is based on statistical learning theory, which is still based on the axiomatic language of probability spaces. This theory is based on traditional statistical theory and developed in the 1960s.Machine learning is divided into multiple categories; in this article, I will focus on supervised learning theory, as it is the easiest to explain (although it remains obscure due to its heavy reliance on mathematical concepts).In supervised learning within statistical learning theory, we are given a dataset, denoted as S= {(xᵢ,yᵢ)}, meaning we have a dataset containing N data points, where each data point is described by other values called “features,” represented by x, which are depicted through a specific function to return the desired y values.Given this dataset, the question is how to find the function that maps x values to y values. We refer to the entire collection of functions that can describe the mapping process as the hypothesis space.To find this function, we need to provide the algorithm with some methods to “learn” how to best approach this problem, which is provided by a concept called the “loss function.” Therefore, for each of our hypotheses (i.e., proposed functions), we measure the performance of this function by comparing the expected risk value across all data.The expected risk is essentially the sum of the loss function multiplied by the probability distribution of the data. If we know the joint probability distribution of this mapping, finding the optimal function would be straightforward. However, this joint probability distribution is usually unknown, so our best approach is to guess an optimal function and empirically verify whether the loss function is optimized. We call this empirical risk.After that, we can compare different functions and find the hypothesis that minimizes the expected risk, which is the hypothesis that yields the smallest lower bound value among all functions.However, to minimize the loss function, the algorithm has a tendency to cheat by overfitting. This is why we need to “learn” the function through the training set, and then validate the function on the data set outside the training set, the test set.How we define the essence of machine learning raises the issue of overfitting, and also explains the need to distinguish between training and testing sets. In statistics, we do not need to attempt to minimize empirical risk; overfitting is not an inherent feature of statistics. The learning algorithm aimed at minimizing empirical risk in statistics is referred to as empirical risk minimization.IllustrationUsing linear regression as a simple example. In traditional concepts, we attempt to minimize the error in the data to find a function that can describe the data, in which case we typically use mean variance. The use of squares is to prevent positive and negative values from canceling each other out. Then we can use a closed-form expression to solve for the regression coefficients.If we consider the loss function as mean variance and minimize empirical risk based on statistical learning theory, we happen to arrive at the same results as traditional linear regression analysis.This coincidence occurs because the two situations are the same; solving for maximum probability on the same data in the same way naturally yields the same result. Maximizing probability can be achieved through different methods to accomplish the same goal, but no one would argue that maximizing probability is the same as linear regression. This simplest example clearly fails to distinguish these methods.Another point to note is that traditional statistical methods do not have the concept of training and testing sets, but we will use different metrics to help validate the model. Although the validation process differs, both methods can yield statistically robust results.Additionally, it should be noted that traditional statistical methods provide us with an optimal solution in closed form, without testing other possible functions to converge on a result. In contrast, machine learning methods attempt a batch of different models, and ultimately combine the results of the regression algorithms to converge on a final hypothesis.If we use a different loss function, the results may not converge. For example, if we use hinge loss (which is not easy to distinguish when using standard gradient descent, so we need to use other methods like near-gradient descent), then the results will differ.Finally, we can distinguish the bias of the model. You can use machine learning algorithms to test linear models as well as polynomial models, exponential models, etc., to check whether these hypotheses provide a better fit to our prior loss function for the dataset. In the traditional statistical concept, we select a model and evaluate its accuracy, but we cannot automatically pick the optimal one from 100 different models. Clearly, due to the initially chosen algorithm being different, the models found will always have some bias. Choosing an algorithm is very necessary because finding the optimal equation for a dataset is an NP-hard problem.So which method is superior?This question is actually quite silly. Without statistics, machine learning could not exist at all, but due to the contemporary information explosion, the vast amount of data accessible to humans makes machine learning very useful.Comparing machine learning and statistical models is even more challenging; you need to choose which one to select based on your objectives. If you simply want to create a highly accurate algorithm for predicting housing prices or find out which group of people is more likely to get a certain disease, machine learning may be the better choice. If you want to identify relationships between variables or draw inferences from the data, choosing a statistical model would be better.
Text in the image:Is this your machine learning system?Yes, you just dump all the data into this big pile or linear algebra, and then take the answer out from the other end.What if the answer is wrong?Then just stir it until it looks right.
If your foundation in statistics is not solid enough, you can still learn and use machine learning – the abstract concepts in machine learning libraries allow you to use them easily as an amateur, but you still need to have some understanding of statistical concepts to avoid overfitting the model or drawing seemingly reasonable conclusions.Related report:https://towardsdatascience.com/the-actual-difference-between-statistics-and-machine-learning-64b49f07ea3?gi=412e8f93e22e
— THE END —