From | Zhihu
Address | https://zhuanlan.zhihu.com/p/270210535
Author | Pan Xiaoxiao
Editor | Machine Learning Algorithms and Natural Language Processing WeChat public account
This article is for academic sharing only. If there is any infringement, please contact us to delete the article.
Word vectors have become a common preprocessing method in the field of NLP. Almost all programs that handle language now have word vectors as their default input. However, for the simplest word2vec, there are still some aspects that we seem to not fully understand.
Word2Vec’s Skip-gram Architecture
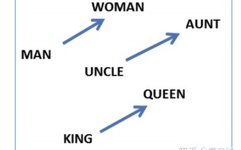
The core idea of Word2Vec is to use shorter vectors to represent different words. The relationships between vectors can represent the relationships between words. In summary, there are two commonly used relationships:
First, the angle between vectors is used to represent the “semantic similarity” between words. The smaller the angle, the more consistent the direction, and thus the more similar the meanings of the words. The other relationship is the hidden dimensions of word meanings. Here is a very famous example:
By subtracting the vectors on both sides, the resulting difference vector is almost identical. This phenomenon occurs because the word vectors in word2vec also hide the abstract dimensions of the words. The vector for “king” minus the vector for “queen” precisely yields the dimension of gender.
These two important properties endow word vectors with powerful capabilities.
To achieve this property, the core is to define what is called “similarity”.
Symbols, glyphs, and pronunciations are not important; the most important thing is the relationship.
For two words, “cat” and “dog”, if they both appear with “pet, cute, animal…”, then “cat” and “dog” are very similar. This is the idea of structuralism.
For convenience in later discussions, we refer to words like “pet, cute, animal” that appear with “cat” as the “context of cat”. The word “cat” is the “target word”.
At this point, if we give both cat and dog a vector and require that this vector predicts their context, we are using the so-called skip-gram algorithm. Since their contexts are almost identical, the input word vectors will also be almost identical. Thus, we achieve an important goal: words that are contextually similar will have similar word vectors.
More accurately, for two co-occurring words i and j, we will optimize a loss function l:
In this function, the first part is the prediction part. The inner product of vector and vector
will yield a larger inner product, resulting in a smaller loss. We can also look at this inner product from a predictive perspective:
being larger means the model believes that i and j co-occurring is more probable. Thus, we can use the dot product of word vectors to predict their context.
The second part of the function is called “negative sampling”. We randomly sample a word n from a distribution and hope that
is as small as possible.
Intuitively, this optimization process does two things:
-
It brings the word vectors
and
closer together;
-
It pushes apart the word vectors
and
that are not connected.
There is a crucial detail here: we are not bringing closer to
, but rather
closer to
. This means that word vector embedding is not simply about bringing co-occurring words closer together, but rather bringing a word closer to its context. Here, w is the embedding of the word, and v is the embedding of the context. It is through this method that we achieve the initial definition of “similarity”—words that have similar contexts will also have similar word vector embeddings.
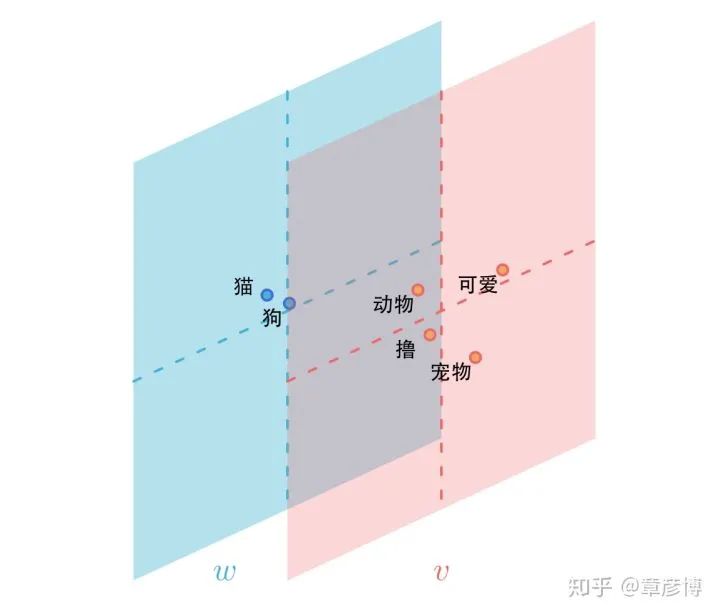
The Two Spaces of Word Vectors
The two spaces of word vector embeddings are often overlooked. In practical applications, the one used is usually just the word embedding, which is w. However, only when w and v are together can we obtain the most complete information. In a niche paper titled “Improving Document Ranking with Dual Word Embeddings”[1], the authors presented an interesting table:
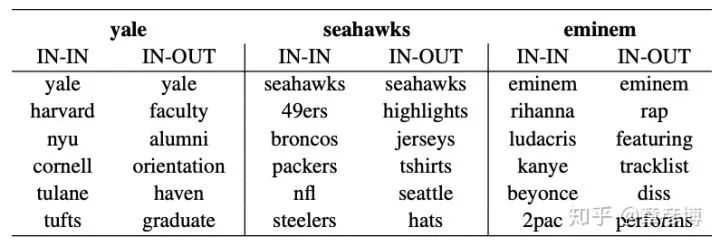
In the table, IN represents the word embedding, which is w; OUT represents the context embedding, which is v. For example, if we examine the word Yale, the closest word embedding to Yale is universities like Harvard, NYU, and Cornell. They share the same property: “they are all universities”.
However, if we examine the relationship between Yale’s word embedding and context embedding, an interesting phenomenon emerges: in the context space, the closest words to Yale’s word vector embedding become terms like faculty, alumni, and orientation. They are all things within the university. In fact, they correspond to the words that co-occur in the data.
The authors also experimented with using IN-OUT instead of IN-IN for some engineering experiments, achieving better results than before. But here we will not elaborate on that; compared to engineering success, this detail can lead to a more interesting point—the skip-gram word vector embedding is essentially performing (weighted) matrix factorization.
The Mathematics of Skip-gram
Now that we know there are two spaces in word vector embeddings, w and v. For and
, their dot product will always yield a scalar
. We can look at it in reverse, considering the training of word vectors as performing matrix factorization on
.
So, the question arises, what is the M matrix?
To answer this question, we need to derive the mathematics of skip-gram from scratch. A paper from 2014[2] provides a detailed derivation, and here I will briefly summarize it.
Initially, I presented the loss contributed by two co-occurring words i and j:
For actual training, the loss must be multiplied by the probability of (i,j) appearing. Therefore, the theoretical expected loss is:
That is:
Here, represents the probability of i and j co-occurring in the data, and the marginal distribution of i.
represents the probability distribution of negative sampling. Through this method, we eliminate the initial
and are left with only
.
Let ; the original expression becomes:
Thus, we only need to solve for to know the form of M:
This form is quite interesting. We consider two distributions for negative sampling: one that makes use the occurrence frequency in the data as negative sampling; the other that makes
a uniform negative sampling, where N is the total number of words.
Substituting the former yields , where PMI stands for Pointwise Mutual Information, which describes a correlation between words i and j, i.e., the degree of uncertainty reduction about whether word j appears given that word i has appeared. The higher the value, the greater the positive association between i and j.
However, if we substitute the latter, will yield
, which is the logarithm of the conditional probability.
At the same time, we can see an interesting result—negative sampling is necessary and not just an embellishing “optimization”. Without negative sampling, k=0. To minimize the loss, M must approach infinity. However, just doing negative sampling for each pair of data is sufficient to eliminate this possibility.
What Exactly Are Word Vectors Doing?
With the theoretical foundation laid, we can finally discuss the behavior of word vectors. What are word vectors modeling? If the word vectors (w) of two words are similar, what exactly are they similar to?
The answer is clear—word vectors are modeling PMI or conditional probabilities. Which one specifically depends on the negative sampling method. Word vectors reduce the dimensionality of the PMI (or conditional probability) matrix through matrix factorization to obtain the vectors we need.
The advantage of word vector decomposition over SVD is that this decomposition is still weighted! Frequently occurring words have smaller reconstruction errors; while infrequently occurring words have greater tolerance for errors. This is something traditional SVD struggles to achieve.
To discuss what “similarity of word vectors” means, we can take PMI as an example to look at a specific question: if the word vectors of two words, such as “cat” and “dog”, are similar, what does that imply? Let’s take a look at the following image:
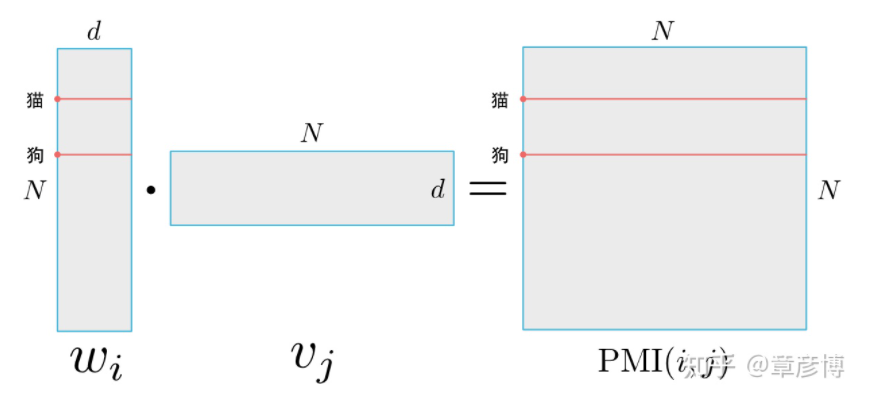
For a training result of N words embedded into d dimensions, when the word vectors for cat and dog are nearly identical, it means that the PMI matrix’s row vectors for cat and dog are almost the same.
This indicates that similar word vectors (w) mean that the two words have similar PMIs with all other words. Alternatively, it means that the conditional probabilities of the contexts of the two words are similar.
There is a very thought-provoking phenomenon here: we are directly training w and v, while M, as a function of w and v, is a very meaningful quantity. How do we reverse this process—if I need PMI, how can I design a simple and elegant training? Moreover, what is being directly trained is not necessarily PMI.
References
-
^Nalisnick, E., Mitra, B., Craswell, N., & Caruana, R. (2016, April). Improving document ranking with dual word embeddings. In Proceedings of the 25th International Conference Companion on World Wide Web (pp. 83-84). https://www.microsoft.com/en-us/research/wp-content/uploads/2016/04/pp1291-Nalisnick.pdf
-
^Levy, O., & Goldberg, Y. (2014). Neural word embedding as implicit matrix factorization. In Advances in neural information processing systems (pp. 2177-2185). http://papers.nips.cc/paper/5477-neural-word-embedding-as-implicit-matrix-factorization.pdf
Download 1: Four-piece Set
Reply "Four-piece Set" in the backend of the Machine Learning Algorithms and Natural Language Processing WeChat public account to obtain the four-piece set for learning TensorFlow, Pytorch, machine learning, and deep learning!
Download 2: Repository Address Sharing
Reply "Code" in the backend of the Machine Learning Algorithms and Natural Language Processing WeChat public account to obtain 195 NAACL papers + 295 ACL2019 papers with open-source code. The open-source address is as follows: https://github.com/yizhen20133868/NLP-Conferences-Code
Heavyweight! The Machine Learning Algorithms and Natural Language Processing group has been officially established! There are plenty of resources in the group, and everyone is welcome to join and learn!
Extra welfare resources! Deep learning and neural networks by Qiu Xipeng, official Chinese tutorial for Pytorch, data analysis using Python, machine learning study notes, official Chinese documentation for pandas, effective java (Chinese version), and 20 other welfare resources
How to obtain: After entering the group, click on the group announcement to get the download link
Note: Please modify the remarks when adding as [School/Company + Name + Direction]
For example - HIT + Zhang San + Dialogue System.
The account owner and micro-businesses are requested to avoid. Thank you!
Recommended Reading:
12 Golden Rules for Solving NER Problems in Industry
Three Steps to Master the Core of Machine Learning: Matrix Derivatives
Distillation Techniques in Neural Networks, Starting from Softmax