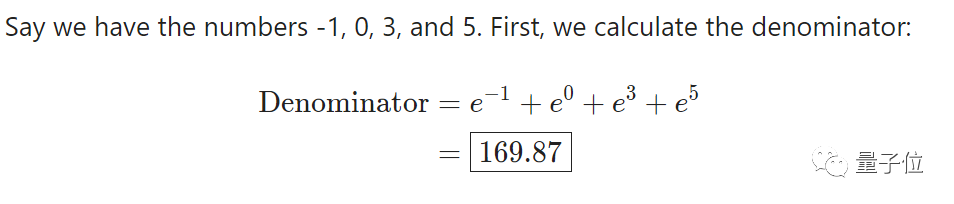This article is authorized for reprint by AI new media Quantum Bit, please contact the source for reprinting.
This article is about 2000 words, and it is recommended to read in 5 minutes.
When it comes to image classification, challenges arise from large images, varying shapes and positions of objects, which poses difficulties for ordinary neural networks. Convolutional Neural Networks (CNNs) are designed to address these issues.
Determine whether you are a person or an object, a cat or a dog.
The most important use of Convolutional Neural Networks (CNNs) is image classification. It seems simple at first glance.
Why not use ordinary neural networks?
This is because image classification faces challenges such as large images and varying shapes and positions of objects, which complicate the use of ordinary neural networks.
Thus, Convolutional Neural Networks are here to solve this problem.
Victor Zhou, a software engineer at Facebook, introduces what Convolutional Neural Networks are in this beginner’s guide.
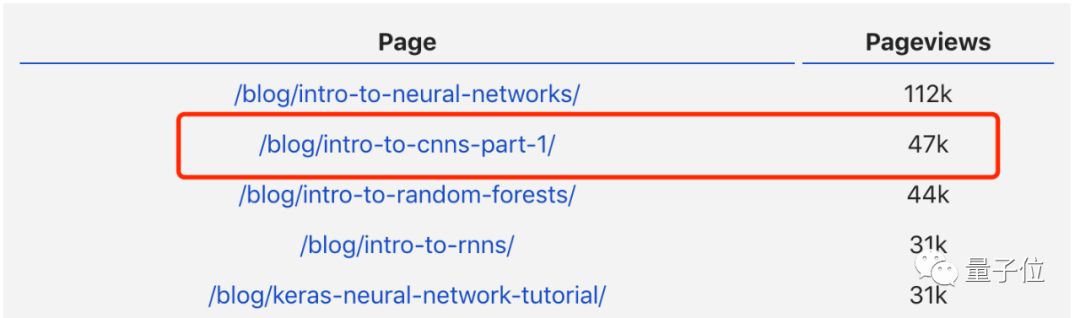
So far, it has received 47k visits.
For those who already have some understanding of neural networks, come and take a look.
MNIST Handwritten Digit Classification
First, let’s take the MNIST handwritten digit classification as an example; here are samples from the MNIST dataset.
It’s simple: recognize the image and classify it as a digit.
Each image in the MNIST dataset is 28×28 pixels, and they are all centered grayscale digits.
Ordinary neural networks can actually solve this problem by treating each image as a 28×28=784-dimensional vector, feeding it into a 784-dimensional input layer, stacking a few hidden layers, and then using an output layer with 10 nodes, one for each digit.
However, these digits are centered, and the images are small, so there are no issues with large sizes or positional offsets. But we know that in real life, it is not the case.
Now that we have a basic understanding, let’s enter the world of Convolutional Neural Networks.
What is a Convolutional Neural Network?
As the name suggests, a Convolutional Neural Network is essentially a neural network composed mainly of convolutional layers, which are based on mathematical operations of convolution.
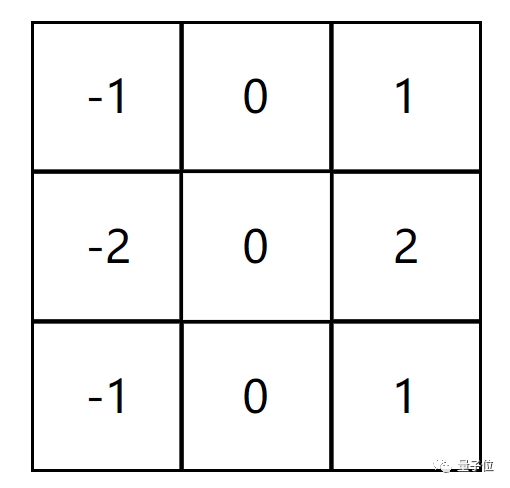
A convolutional layer consists of a set of filters, which can be viewed as numbers in a two-dimensional matrix. For example, here is a 3×3 filter.
The convolution operation combines the input image with the filter to generate an image, which includes:
-
Overlaying the filter on a specific position of the image.
-
Performing element-wise multiplication between the values in the filter and the corresponding values in the image.
-
Summing all the products of the elements. This sum becomes the output value of the target pixel in the output image.
-
Repeating for all positions.
This might sound a bit abstract. Don’t worry, an example is coming.
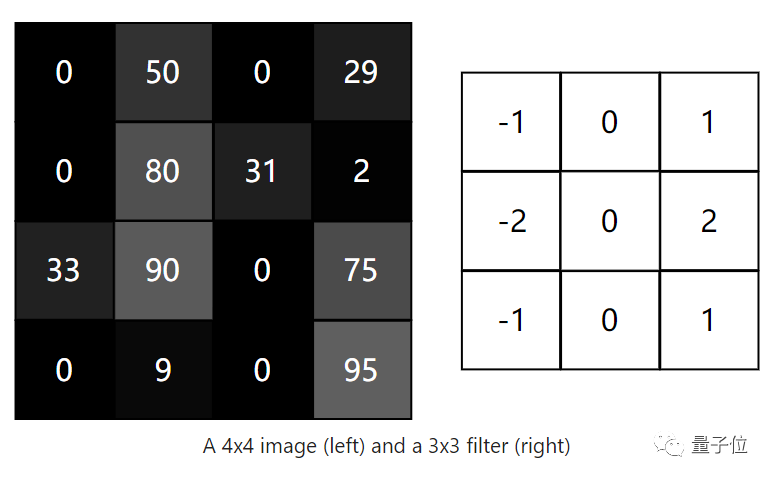
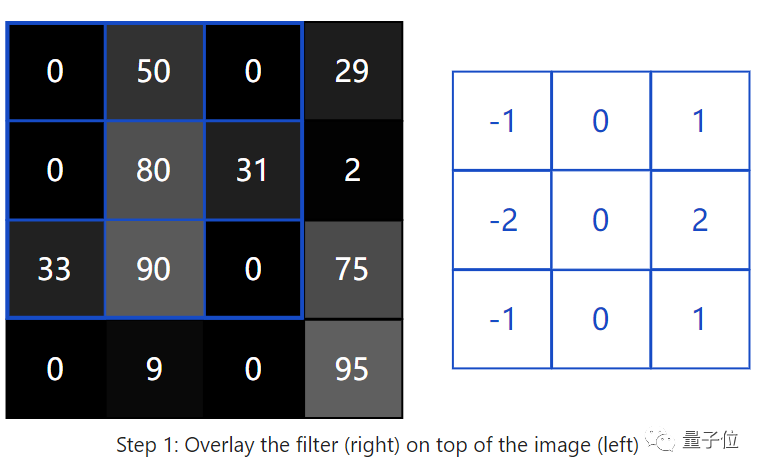
Let’s take a small 4×4 grayscale image and a 3×3 filter as an example.
The numbers in the image represent pixel intensities, where 0 is black and 255 is white. We will set our output to be a 2×2 output image.
First, we overlay our filter on the top-left position of the image.
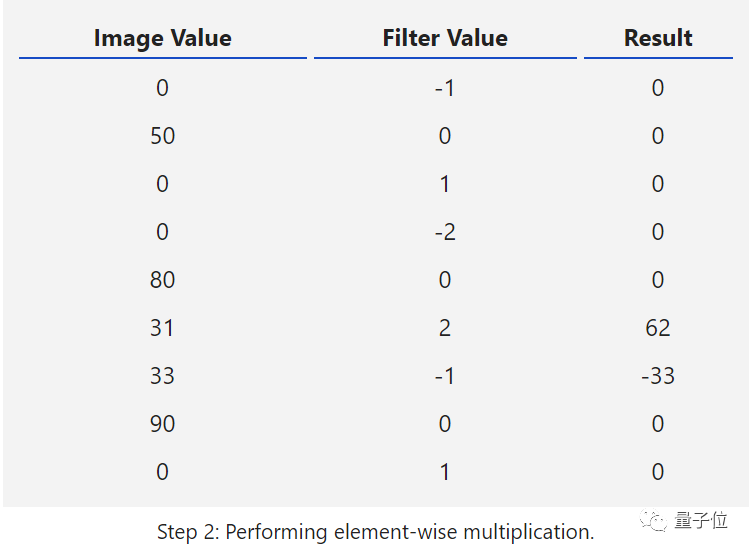
Next, we perform element-wise multiplication between the two values (image value and filter value). This results in the following table:
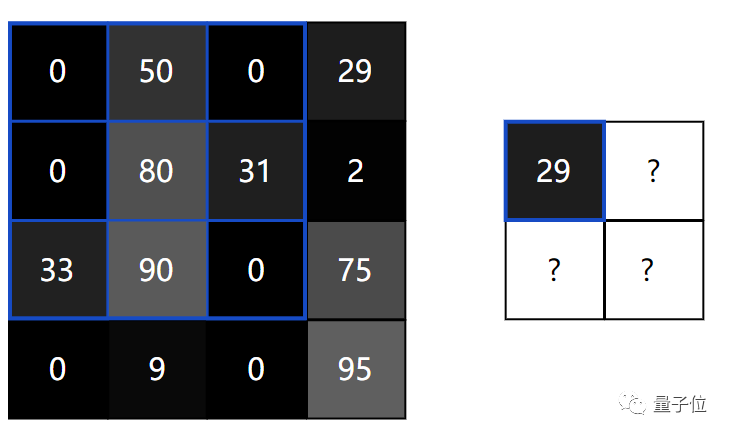
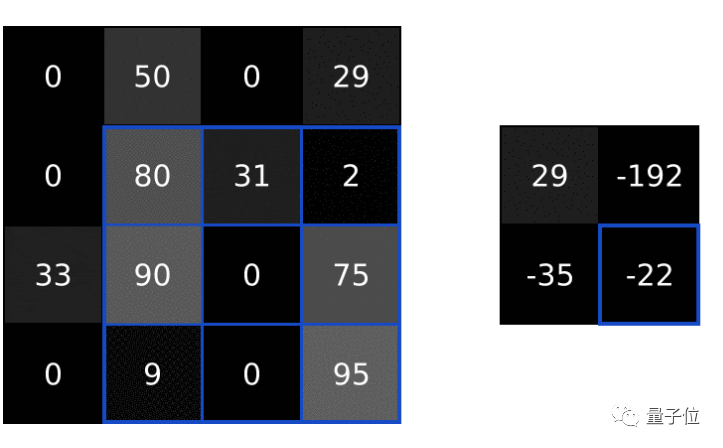
Continuing this way, we can obtain the values for the 2×2 image.
What is the use of Convolution?
Let’s put the use of convolution aside for a moment and take a look at the image.
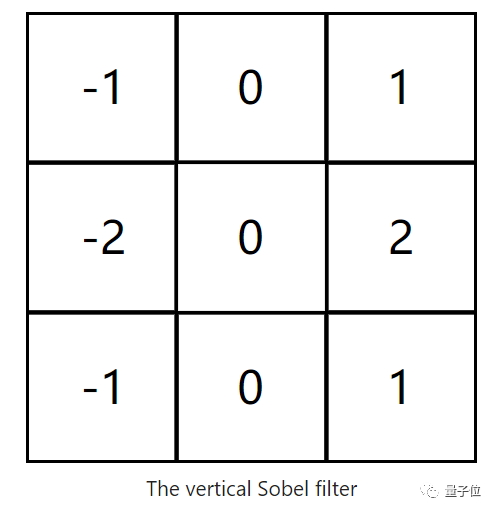
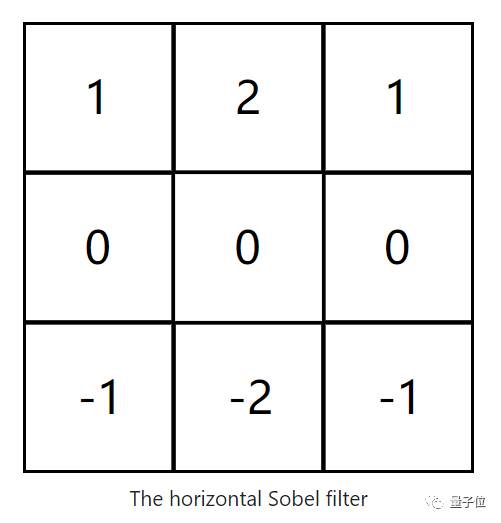
Isn’t this the 3×3 filter we just saw? In fact, it has a professional name—Vertical Sobel Filter, and there is also a Horizontal Sobel Filter, which has a row of zeros in the middle.
In fact, Sobel filters are edge detectors; the Vertical Sobel Filter detects vertical edges, while the Horizontal Sobel Filter detects horizontal edges.
This might not be very clear. Let’s take a look at the image.
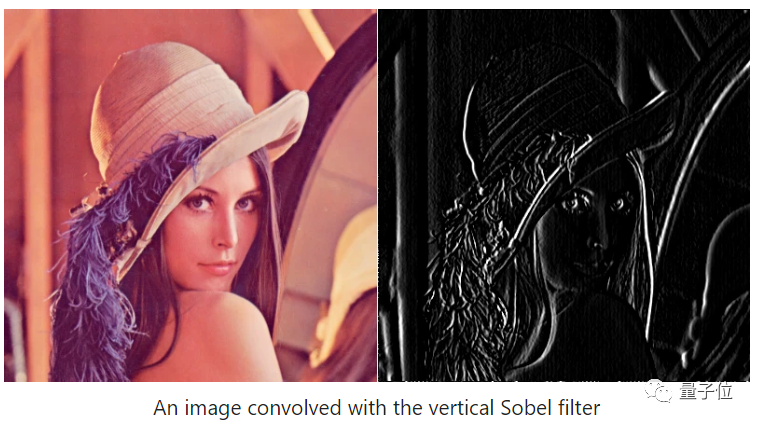
Imagine if both filters are used; wouldn’t convolution be able to capture the edge features of the image?
Bright pixels in the output image indicate that the original image has strong edges around it.
Thus, convolution can help us find specific local image features, such as edges.
Padding
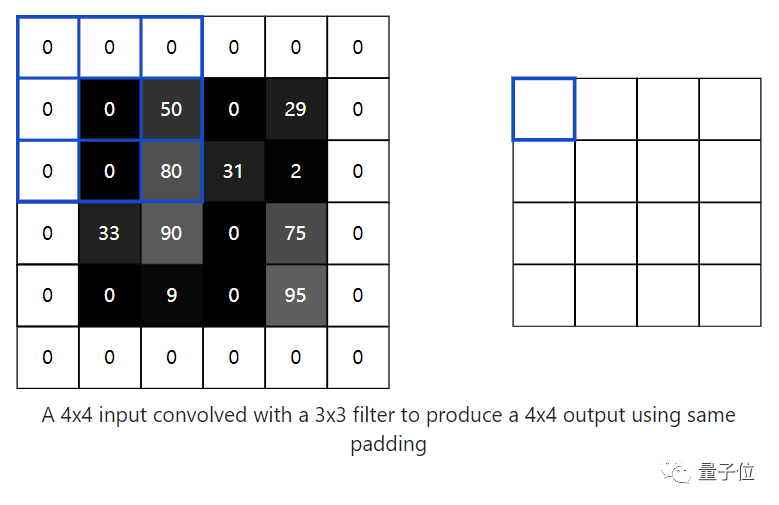
Generally, we want the output image to be the same size as the original image. However, in the example above, we used a 4×4 image as input and got a 2×2 image as output. How do we solve this problem?
Padding. This is where the magic of zeros comes into play.
We need to add a layer of “0” around the image, and the filter also needs to be padded by 1 pixel.
In this way, the output image has the same dimensions as the input image, called same padding.
Convolution Layer
The convolution layer contains the set of filters mentioned above, and the main parameter of the convolution layer is the number of filters.
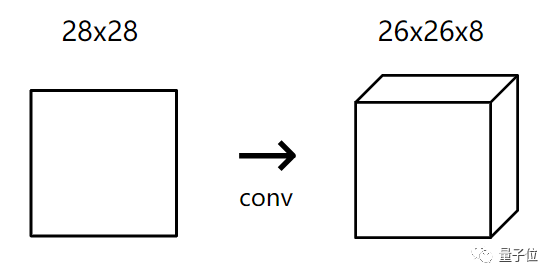
For MNIST CNN, if we use a small convolutional layer with 8 filters, the input will be 28×28, and the output will become 26×26×8.
(Because of valid padding, it will reduce the height and width of the input by 2)
Pooling Layer
Adjacent pixels in an image often have similar values, and after passing through the convolution layer, similar values can be produced among adjacent pixels. This can lead to redundancy in the information output by the convolution layer.
For example, the filter responsible for edge detection can find strong edges at a certain position, but it is also likely to find strong edges in an adjacent pixel, resulting in the presence of two identical edges simultaneously.
This causes information redundancy and prevents the discovery of new information.
Pooling solves this problem. Pooling reduces the size of the input by concentrating the values.
Typically, this is done through a simple operation, such as taking the max, min, or average value.
Below is an example of a max pooling layer with a pooling size of 2. To perform max pooling, we traverse the input image with 2×2 blocks and place the maximum value into the corresponding pixel of the output image.
Pooling reduces the width and height of the input by the pooling size.
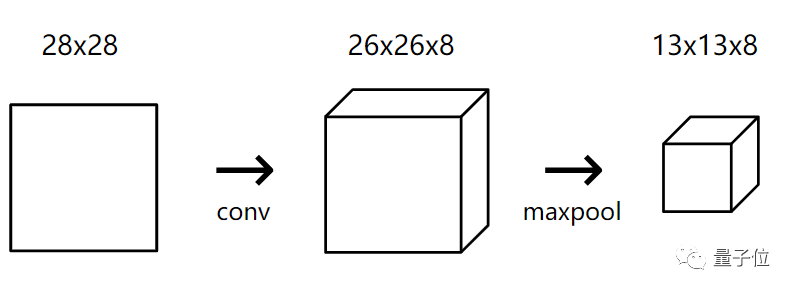
For our MNIST CNN, we will immediately place a max pooling layer with a pooling size of 2 after the initial transformation layer. The pooling layer will convert the 26x26x8 input into a 13x13x8 output.
Softmax Layer
In fact, to complete CNN, we also need to endow it with predictive capabilities.
We will do this by using the standard final layer for multi-class classification problems: the Softmax layer, which is a fully connected (dense) layer that uses the Softmax function as its activation.
What is the Softmax Function?
Given some numbers, the Softmax function can convert any number into a probability.
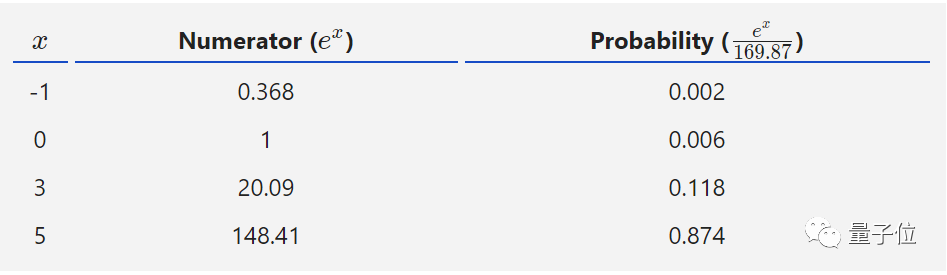
For example, let’s select the numbers -1, 0, 3, and 5.
First, we need to calculate the exponentials of the specified numbers and then sum all results to serve as the denominator.
Finally, the values of the exponentials serve as the numerator, thus calculating the probabilities.
Taking MNIST CNN as an example, we will use a softmax layer with 10 nodes as the last layer of the CNN, with each node representing a digit. Each node in the layer will connect to each input.
After applying the softmax transformation, the digit represented by the node with the highest probability will be the output of the CNN.
Now that we have covered so much, do you have a good understanding of Convolutional Neural Networks?
You can click the link below for more information~
Portal:
https://victorzhou.com/blog/intro-to-cnns-part-1/
https://victorzhou.com/blog/softmax/