Lightweight Backbone Dominance | VGNetG Achieves 'Want It All Without Choices' Lightweight Backbone Network!

Modern efficient convolutional neural networks (CNN) always use depthwise separable convolutions (DSC) and neural architecture search (NAS) to reduce the number of parameters and computational complexity. However, they overlook some inherent features of the network. Inspired by visual feature maps and N×N (N>1) convolution kernels, this paper introduces several guidelines to further improve parameter efficiency and inference speed.

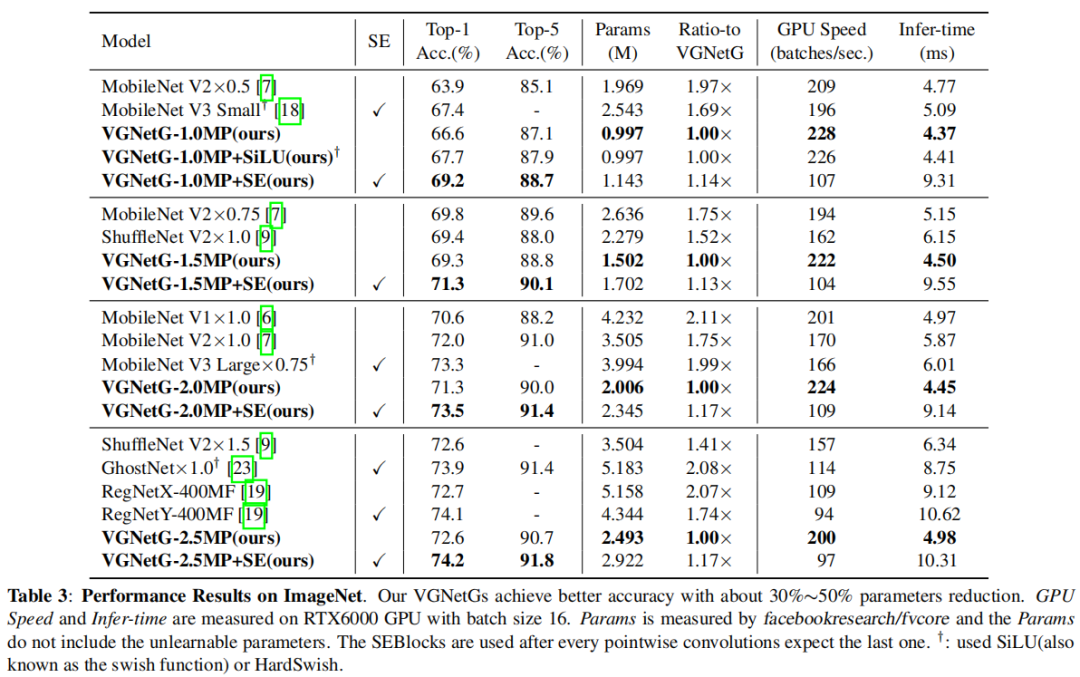
The parameter-efficient CNN architecture designed based on these guidelines is called VGNetG, which achieves better accuracy and lower latency compared to previous networks, with a reduction in parameters by about 30%~50%. VGNetG-1.0MP achieved 67.7% top-1 accuracy with 0.99M parameters on the ImageNet classification dataset, and 69.2% top-1 accuracy with 1.14M parameters.

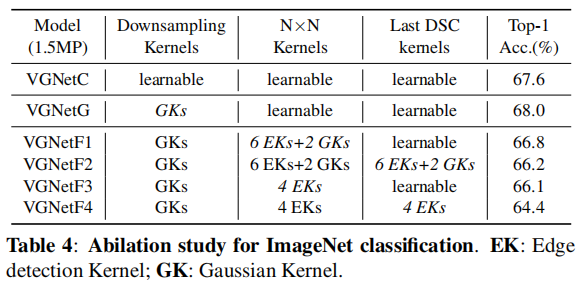
Additionally, it is demonstrated that edge detectors can replace learnable depthwise convolution layers by using fixed edge detection kernels instead of N×N kernels to mix features. VGNetF-1.5MP achieved 64.4% (-3.2%) top-1 accuracy and 66.2% (-1.4%) top-1 accuracy with additional Gaussian kernels.

1Methodology

The authors mainly studied three typical networks constructed by standard convolutions:

Standard Convolution ==> ResNet-RS,
Group Convolution ==> RegNet,
Depthwise Separable Convolution ==> MobileNet, ShuffleNetV2, and EfficientNets.

These visual results indicate that M×N×N kernels exhibit significantly different patterns and distributions at various stages of the network.

1.1 CNNs Can Learn to Satisfy the Sampling Theorem

Previous work has assumed that convolutional neural networks ignore the classical sampling theorem, but the authors found that CNNs can satisfy the sampling theorem to some extent by learning low-pass filters, especially networks based on DSCs, such as MobileNetV1 and EfficientNets, as shown in Figure 2.

1. Standard Convolution/Group Convolution

As shown in Figures 2a and 2b, there exists one or more significant N×N kernels among the entire M×N×N kernels, such as the blurring kernel, indicating that the parameters of these layers are redundant. Note that significant kernels do not necessarily resemble Gaussian kernels.

2. Depthwise Separable Convolution

Strided-DSC kernels usually resemble Gaussian kernels, including but not limited to MobileNetV1, MobileNetV2, MobileNetV3, ShuffleNetV2, ReXNet, and EfficientNets. Moreover, the distribution of Strided-DSC kernels is not Gaussian but rather a Gaussian mixture distribution.

3. Kernels of the Last Convolution Layer

Modern CNNs always use a global pooling layer before the classifier to reduce dimensionality. Therefore, similar phenomena also occur in the last depthwise convolution layer, as shown in Figure 4.

These visualizations suggest that depthwise convolutions should be chosen over standard and group convolutions in downsampling layers and the last layer. Additionally, fixed Gaussian kernels can be used in downsampling layers.

1.2 Reusing Feature Maps Between Adjacent Layers

Identity Kernel and Similar Feature Maps

As shown in the above figure, many depthwise convolution kernels have large values only at the center, similar to the identity kernel in the middle part of the network. Since the input is merely passed to the next layer, convolutions with identity kernels lead to feature map duplication and computational redundancy. On the other hand, the following figure shows that many feature maps are similar (repeated) between adjacent layers.

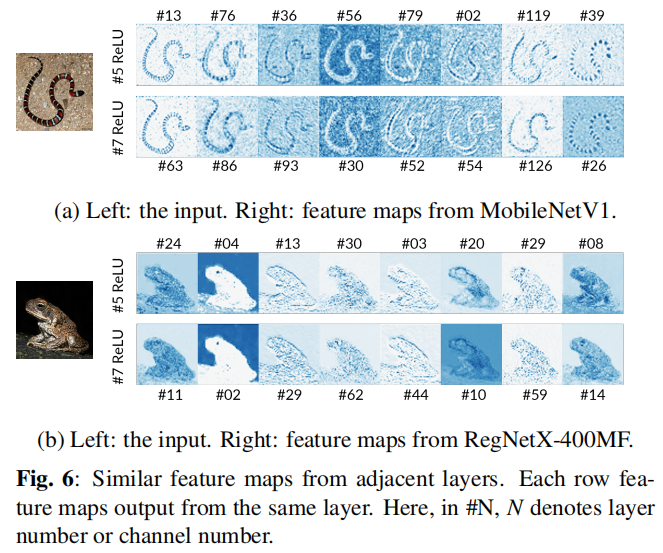
Therefore, parts of convolutions can be replaced with identity mapping. Otherwise, depthwise convolutions in early layers are slow because they often do not fully utilize modern accelerators reported in Shufflenet V2. Thus, this approach can improve parameter efficiency and inference time.

1.3 Edge Detectors as Learnable Depthwise Convolutions

Edge features contain important information about images. As shown in the figure below, most kernels approximate edge detection kernels, such as the Sobel filter kernel and Laplace filter kernel. The proportion of such kernels decreases in later layers, while the proportion of kernels resembling blurring kernels increases.

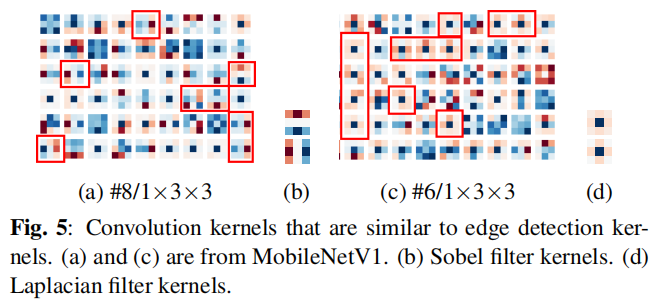
Therefore, perhaps edge detectors can replace depthwise convolutions based on DSC networks to mix features between different spatial locations. The authors will demonstrate this by replacing learnable kernels with edge detection kernels.

2Network Architecture

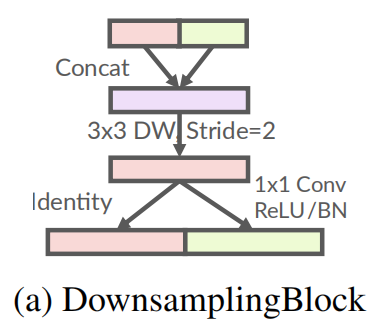
2.1 DownsamplingBlock

DownsamplingBlock halves the resolution and expands the number of channels. As shown in Figure a, channel expansion is generated by pointwise convolutions to reuse features. The kernels of depthwise convolutions can be randomly initialized or use fixed Gaussian kernels.

2.2 HalfIdentityBlock

As shown in Figure b, half-depth convolutions are replaced with identity mappings while reducing half pointwise convolutions, maintaining block width.

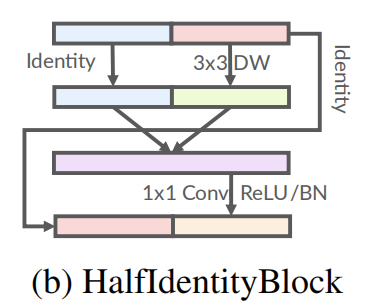
Note that the right half channel of the input becomes the left half channel of the output for better feature reuse.

2.3 VGNet Architecture

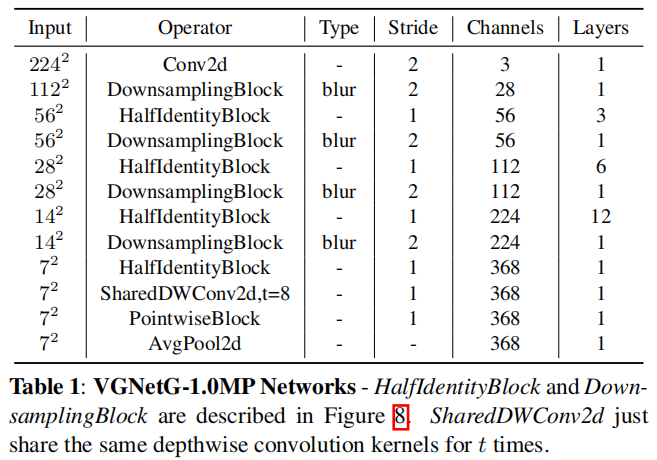
The parameter-limited VGNets are constructed using DownsamplingBlock and HalfIdentityBlock. The overall VGNetG-1.0MP architecture is shown in Table 1.

2.4 Variants of VGNet

To further investigate the effects of N×N kernels, several variants of VGNets are introduced: VGNetC, VGNetG, and VGNetF.

VGNetC: All parameters are randomly initialized and learnable.

VGNetG: All parameters except for the kernels of DownsamplingBlock are randomly initialized and learnable.

VGNetF: All parameters of depthwise convolutions are fixed.

3Experiments

4References

[1]. EFFICIENT CNN ARCHITECTURE DESIGN GUIDED BY VISUALIZATION.

Recommended Reading

Deep Understanding of Generative Models VAE

The Principle and Implementation of DropBlock

How SOTA Model Swin Transformer is Created!

Stylish and Functional! The Generative Model VQ-VAE is Here!

Integrating YYDS! Making Your Model Faster and More Accurate!

Auxiliary Modules Accelerate Convergence, Significantly Improve Accuracy! The Real-Time NanoDet-Plus for Mobile is Here!

SimMIM: A Simpler MIM Method

Detailed Implementation of SSD’s Torchvision Version

Machine Learning Algorithm Engineer

A Caring Public Account