Skip to content
Original Source: Machine Heart
Edited by: Big Plate Chicken
This article introduces a new research on an approximate attention mechanism, HyperAttention, proposed by institutions such as Yale University and Google Research, which accelerates inference time for ChatGLM2 with a context length of 32k by 50%.
Transformers have been successfully applied to various learning tasks in natural language processing, computer vision, and time series forecasting. Despite their success, these models still face severe scalability limitations due to the quadratic (in sequence length) runtime and memory complexity caused by the precise computation of their attention layers. This presents a fundamental challenge in scaling Transformer models to longer context lengths.
The industry has explored various methods to address the quadratic time attention layer issue, one notable direction being the intermediate matrices in approximate attention layers. Approaches to achieve this include approximations through sparse matrices, low-rank matrices, or a combination of both.
However, these methods do not provide end-to-end guarantees for the approximation of the attention output matrix. These approaches aim to approximate various components of attention faster, but none provide a complete end-to-end approximation for dot-product attention. They also do not support the use of causal masks, which are a crucial component of modern Transformer architectures. Recent theoretical boundaries indicate that, in general, it is impossible to perform term-wise approximations of the attention matrix in sub-quadratic time.
However, a recent study called KDEFormer has shown that under the assumption of bounded attention matrix terms, it can provide provable approximations in sub-quadratic time. Theoretically, the runtime of KDEFormer is approximately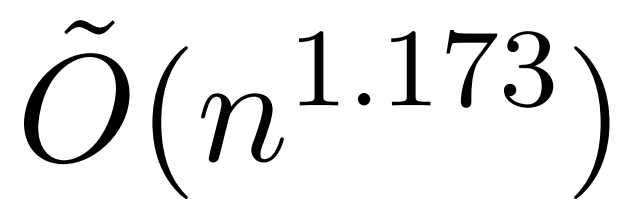 ; it employs Kernel Density Estimation (KDE) to approximate the column norms, allowing for the calculation of probabilities for sampling columns of the attention matrix.However, current KDE algorithms lack practical efficiency, and even theoretically, there is a gap between the runtime of KDEFormer and the theoretically feasible O(n) time algorithms.In this paper, the authors prove that under the same bounded entry hypothesis, a near-linear time
; it employs Kernel Density Estimation (KDE) to approximate the column norms, allowing for the calculation of probabilities for sampling columns of the attention matrix.However, current KDE algorithms lack practical efficiency, and even theoretically, there is a gap between the runtime of KDEFormer and the theoretically feasible O(n) time algorithms.In this paper, the authors prove that under the same bounded entry hypothesis, a near-linear time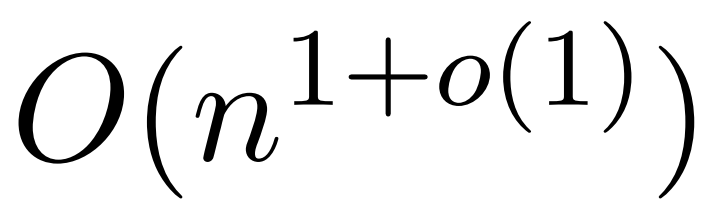 algorithm is possible.However, their algorithm also involves using polynomial methods to approximate softmax, which may not be practical.
In this paper, researchers from Yale University, Google Research, and other institutions provide a win-win algorithm that is both practically efficient and can achieve optimal near-linear time guarantees.Additionally, this method supports causal masks, which were previously impossible to implement.
algorithm is possible.However, their algorithm also involves using polynomial methods to approximate softmax, which may not be practical.
In this paper, researchers from Yale University, Google Research, and other institutions provide a win-win algorithm that is both practically efficient and can achieve optimal near-linear time guarantees.Additionally, this method supports causal masks, which were previously impossible to implement.

Paper link: https://arxiv.org/abs/2310.05869
This paper proposes an approximate attention mechanism called “HyperAttention” to address the computational challenges posed by the increasingly complex long contexts used in large language models. Recent work indicates that in the worst case, quadratic time is necessary unless the entries of the attention matrix are bounded or the matrix’s stable rank is low.
The researchers introduce two parameters to measure: (1) the maximum column norm in the normalized attention matrix, and (2) the ratio of the row norms in the non-normalized attention matrix after detecting and removing large entries. They use these fine-grained parameters to reflect the difficulty of the problem. As long as the above parameters are small, it is possible to achieve linear-time sampling algorithms even if the matrix has unbounded entries or a large stable rank.
HyperAttention features a modular design that allows for easy integration of other fast underlying implementations, especially FlashAttention. Empirically, by using the LSH algorithm to identify large entries, HyperAttention outperforms existing methods, achieving significant speed improvements compared to state-of-the-art solutions like FlashAttention. The researchers validated the performance of HyperAttention on various long context length datasets.
For instance, HyperAttention accelerated inference time for ChatGLM2 with a context length of 32k by 50%, while perplexity increased from 5.6 to 6.3. With larger context lengths (e.g., 131k) and causal masks, HyperAttention achieved a 5-fold speedup on a single attention layer.
Dot-product attention involves processing three input matrices: Q (queries), K (keys), and V (values), all of size nxd, where n is the number of tokens in the input sequence and d is the dimension of the latent representation. The output of this process is as follows:
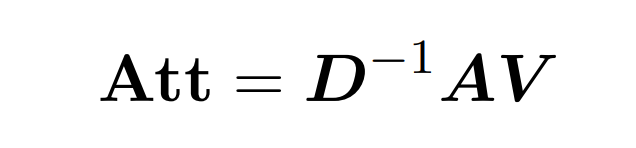
Here, matrix A := exp(QK^T) is defined as the element-wise exponent of QK^T. D is an n×n diagonal matrix derived from the sum of each row of A, where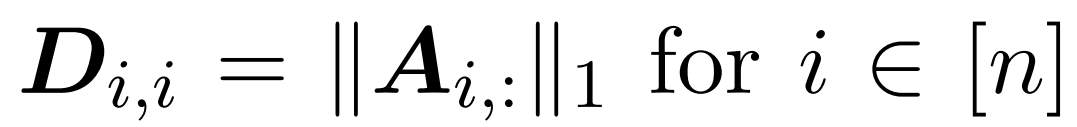 . In this case, matrix A is called the “attention matrix,” and (D^-1) A is called the “softmax matrix.” It is worth noting that directly computing the attention matrix A requires Θ(n²d) operations, and storing it consumes Θ(n²) memory.Therefore, directly computing Att requires Ω(n²d) runtime and Ω(n²) memory.
The researchers’ goal is to efficiently approximate the output matrix Att while preserving its spectral properties. Their strategy includes designing an efficient estimator for the diagonal scaling matrix D in near-linear time. Additionally, they quickly approximate the matrix product of the softmax matrix D^-1A through subsampling. More specifically, they aim to find a sampling matrix with a limited number of rows
. In this case, matrix A is called the “attention matrix,” and (D^-1) A is called the “softmax matrix.” It is worth noting that directly computing the attention matrix A requires Θ(n²d) operations, and storing it consumes Θ(n²) memory.Therefore, directly computing Att requires Ω(n²d) runtime and Ω(n²) memory.
The researchers’ goal is to efficiently approximate the output matrix Att while preserving its spectral properties. Their strategy includes designing an efficient estimator for the diagonal scaling matrix D in near-linear time. Additionally, they quickly approximate the matrix product of the softmax matrix D^-1A through subsampling. More specifically, they aim to find a sampling matrix with a limited number of rows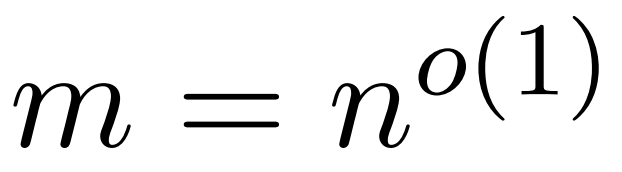 and a diagonal matrix
and a diagonal matrix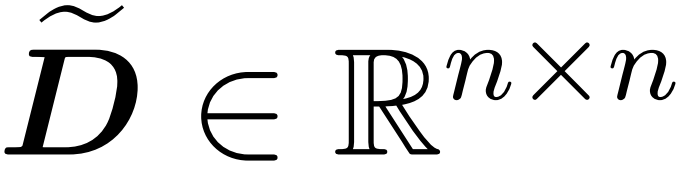 , satisfying the following constraints of the operator norm of the error:
, satisfying the following constraints of the operator norm of the error:
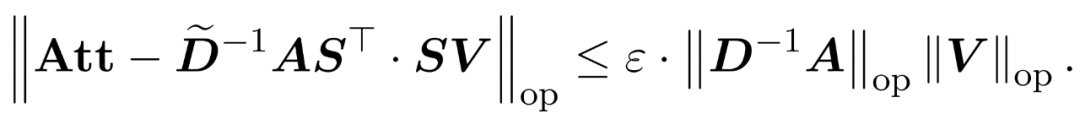
The researchers demonstrate that by defining the sampling matrix S based on the row norms of V, they can efficiently solve the matrix multiplication part of the attention approximation problem in formula (1). The more challenging problem is how to obtain a reliable approximation for the diagonal matrix D. In recent results, Zandieh effectively utilized a fast KDE solver to obtain high-quality approximations for D. The researchers simplified the KDEformer procedure and proved that uniform sampling is sufficient to achieve the desired spectral guarantees without the need for important sampling based on kernel density. This significant simplification enabled them to develop a practical, provable linear-time algorithm.
Unlike previous research, the method in this paper does not require bounded entries or bounded stable rank. Furthermore, even if the entries in the attention matrix or stable rank are large, the fine-grained parameters introduced for analyzing time complexity may still be small.
As a result, HyperAttention shows significant speed improvements, achieving over 50 times faster forward and backward propagation at a sequence length of n=131k. When handling causal masks, the method still achieves a remarkable 5-fold speed increase. Moreover, when applied to pretrained LLMs (such as chatqlm2-6b-32k) and evaluated on the long context benchmark dataset LongBench, it maintains performance levels close to the original model even without fine-tuning. The researchers also evaluated specific tasks and found that summarization and code completion tasks are more significantly impacted by the approximate attention layers than question-answering tasks.
To achieve spectral guarantees when approximating Att, the first step in this paper is to obtain a 1 ± ε approximation of the diagonal entries of matrix D. Subsequently, the matrix product between D^-1 and A and V is approximated through sampling based on the square row ℓ₂-norms of V.
The process of approximating D involves two steps. First, an algorithm rooted in Hamming sorting LSH is used to identify the main entries in the attention matrix, as defined in Definition 1. The second step is to randomly select a small subset K. This paper will prove that under certain mild assumptions on matrices A and D, this simple method can establish spectral bounds for the estimated matrices. The researchers’ goal is to find a sufficiently accurate approximate matrix D that satisfies:

The assumption of this paper is that the column norms of the softmax matrix exhibit a relatively uniform distribution. More accurately, the researchers assume that for any i ∈ [n] t there exists some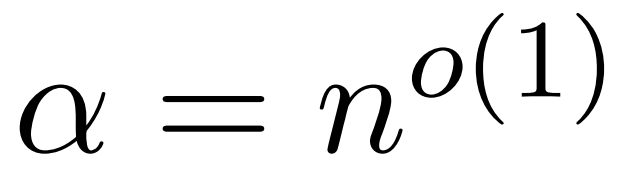 such that
such that .
The first step of the algorithm is to use Hamming sorting LSH (sortLSH) to hash keys and queries into uniformly sized buckets, thereby identifying large entries in the attention matrix A. Algorithm 1 details this process, and Figure 1 visually illustrates the process.
.
The first step of the algorithm is to use Hamming sorting LSH (sortLSH) to hash keys and queries into uniformly sized buckets, thereby identifying large entries in the attention matrix A. Algorithm 1 details this process, and Figure 1 visually illustrates the process.
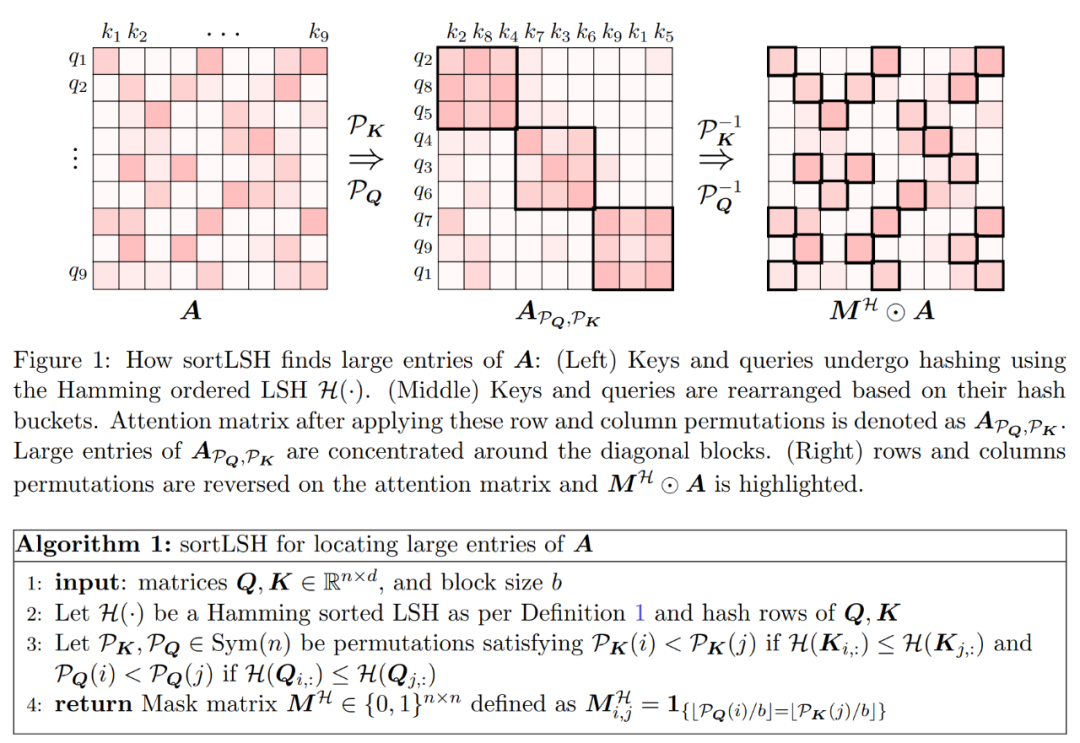
Algorithm 1 returns a sparse mask aimed at isolating the main entries of the attention matrix. Given this mask, the researchers compute an approximation of matrix D in Algorithm 2, which satisfies the spectral guarantees in formula (2). This algorithm achieves this by combining the attention values corresponding to the mask with a randomly selected subset of columns from the attention matrix. The algorithm presented in this paper is versatile and can effectively utilize predefined masks specifying the locations of the main entries in the attention matrix. The primary guarantees provided by this algorithm are given in Theorem 1.


Integrating approximate diagonals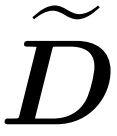 and approximating
and approximating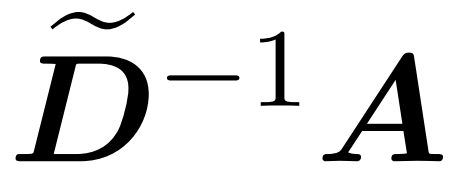 the matrix product between the value matrix V. Thus, the researchers introduce HyperAttention, an efficient algorithm that can approximate the attention mechanism with spectral guarantees in near-linear time. Algorithm 3 takes the mask MH, which defines the positions of the dominant entries in the attention matrix, as input. This mask can be generated using the sortLSH algorithm (Algorithm 1) or can be a predefined mask similar to methods in [7]. The researchers assume that the large entry mask M^H is designed to be sparse, and its number of non-zero entries is bounded
the matrix product between the value matrix V. Thus, the researchers introduce HyperAttention, an efficient algorithm that can approximate the attention mechanism with spectral guarantees in near-linear time. Algorithm 3 takes the mask MH, which defines the positions of the dominant entries in the attention matrix, as input. This mask can be generated using the sortLSH algorithm (Algorithm 1) or can be a predefined mask similar to methods in [7]. The researchers assume that the large entry mask M^H is designed to be sparse, and its number of non-zero entries is bounded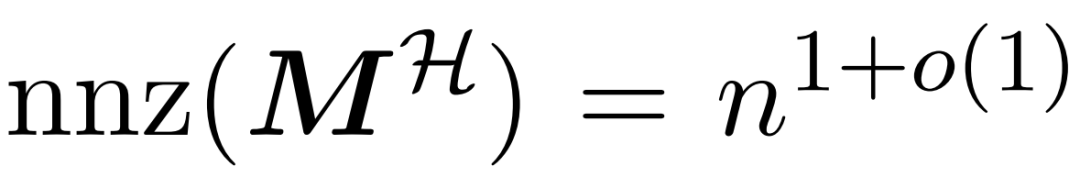 .
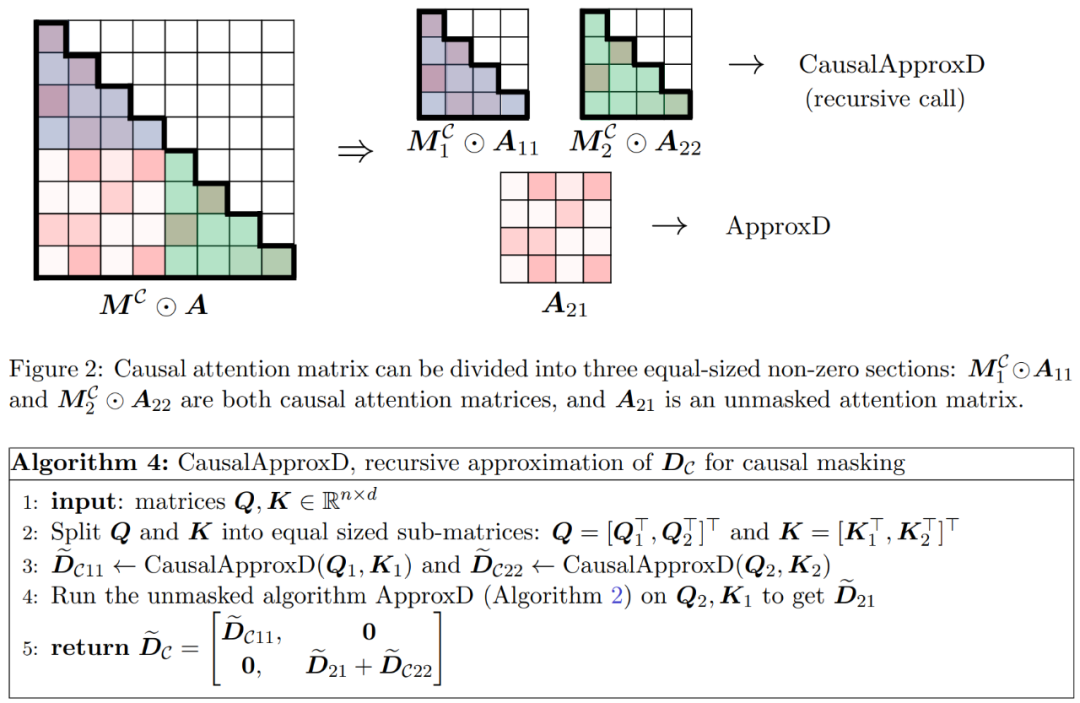
As shown in Figure 2, the method in this paper is based on an important observation. The masked attention M^C⊙A can be decomposed into three non-zero matrices, each of size half of the original attention matrix. The block A_21, completely below the diagonal, represents the unmasked attention. Therefore, we can use Algorithm 2 to approximate its row sum.
The two diagonal blocks shown in Figure 2
.
As shown in Figure 2, the method in this paper is based on an important observation. The masked attention M^C⊙A can be decomposed into three non-zero matrices, each of size half of the original attention matrix. The block A_21, completely below the diagonal, represents the unmasked attention. Therefore, we can use Algorithm 2 to approximate its row sum.
The two diagonal blocks shown in Figure 2 and
and represent causal attention, which is only half the size of the original. To handle these causal relationships, the researchers use a recursive approach, further splitting them into smaller blocks and repeating this process. Pseudocode for this process is given in Algorithm 4.
represent causal attention, which is only half the size of the original. To handle these causal relationships, the researchers use a recursive approach, further splitting them into smaller blocks and repeating this process. Pseudocode for this process is given in Algorithm 4.
The researchers benchmarked the algorithm by extending existing large language models to handle long-range sequences. All experiments were run on a single 40GB A100 GPU and used FlashAttention 2 for accurate attention calculations.
Monkey Patching Self-Attention
The researchers first evaluated HyperAttention on two pretrained LLMs, selecting two widely used models with different architectures: chatglm2-6b-32k and phi-1.5.
In practice, they patched the final ℓ attention layers by replacing them with HyperAttention, where ℓ can range from 0 to the total number of attention layers in each LLM. Note that both models require causal masks for attention, and Algorithm 4 is recursively applied until the input sequence length n is less than 4,096. For all sequence lengths, the researchers set the bucket size b and the number of sampled columns m to 256. They evaluated the performance of such monkey-patched models in terms of perplexity and acceleration.
Simultaneously, the researchers used a collection of long-context benchmark datasets called LongBench, which contains six different tasks: single/multi-document question answering, summarization, few-shot learning, synthesis tasks, and code completion. They selected subsets of datasets with encoded sequence lengths greater than 32,768 and pruned them if they exceeded that length. They then calculated the perplexity for each model, which is the loss of predicting the next token. To highlight the scalability of long sequences, the researchers also calculated the total acceleration of all attention layers, whether performed by HyperAttention or FlashAttention.
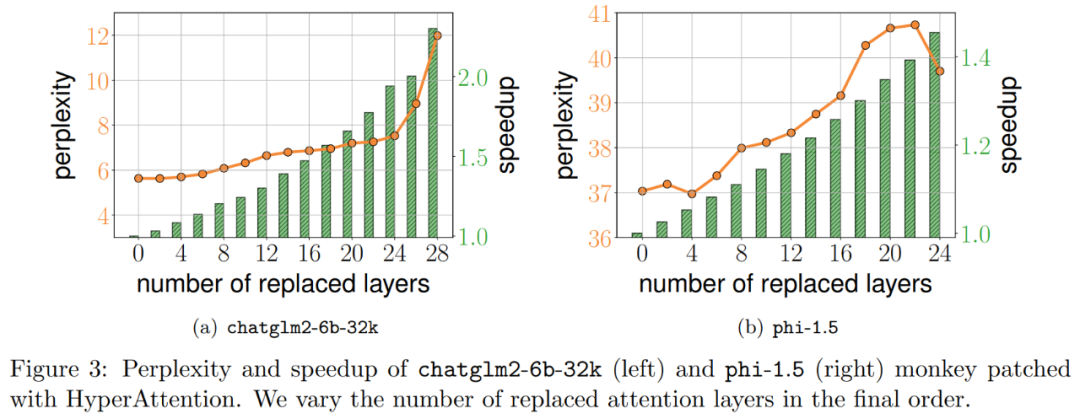
The results are shown in Figure 3, where even after monkey patching with HyperAttention, chatglm2-6b-32k still shows reasonable perplexity. For example, after replacing 20 layers, the perplexity increases by about 1 and continues to rise slowly until reaching 24 layers. The runtime of the attention layers improved by about 50%. If all layers are replaced, the perplexity rises to 12, and the speedup is 2.3. The phi-1.5 model also exhibited similar behavior, but the perplexity increases linearly with the number of HyperAttention layers.
Additionally, the researchers evaluated the performance of the monkey-patched chatglm2-6b-32k on the LongBench dataset and calculated evaluation scores for each task, such as single/multi-document question answering, summarization, few-shot learning, synthesis tasks, and code completion. The results are shown in Table 1.
Although replacing with HyperAttention generally leads to a performance decline, they observed that its impact varies based on the task at hand. For instance, summarization and code completion tasks exhibited the strongest robustness compared to other tasks.
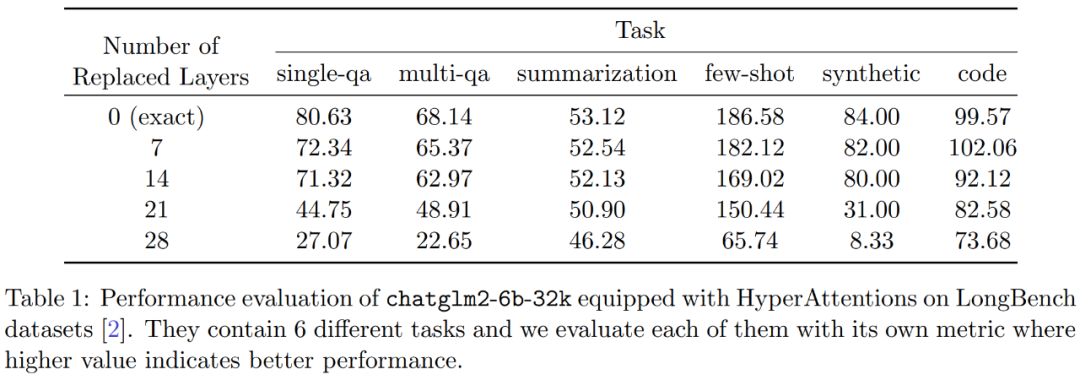
A significant point is that after patching half of the attention layers (i.e., 14 layers), the researchers confirmed that the performance drop for most tasks does not exceed 13%. Particularly for the summarization task, its performance remains nearly unchanged, indicating that this task is most robust to partial modifications in the attention mechanism. When n=32k, the computation speed of the attention layers improved by 1.5 times.
Single Self-Attention Layer
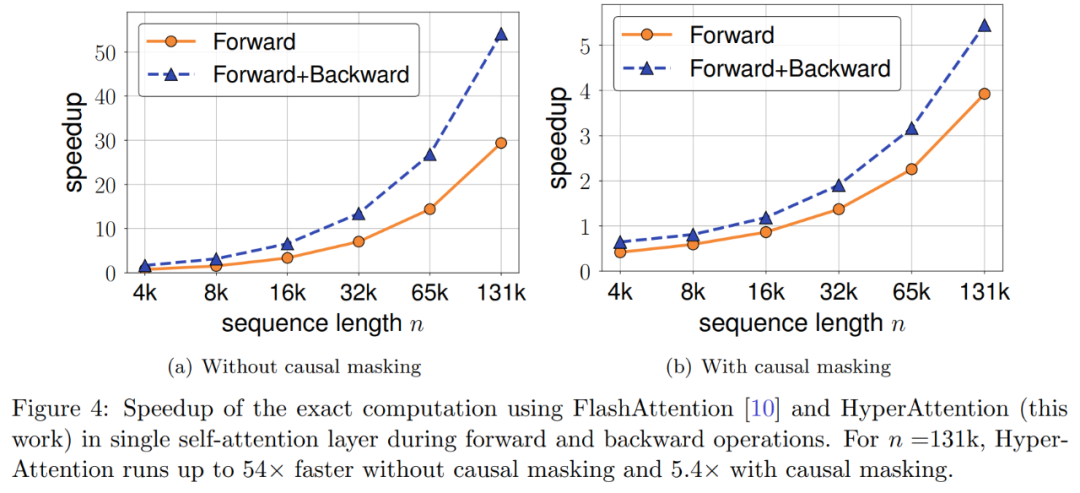
The researchers further explored the acceleration of HyperAttention when the sequence length varies from 4,096 to 131,072. They measured the wall-clock time for forward and forward + backward operations when using FlashAttention for computation or accelerating through HyperAttention. They also measured the wall-clock time with and without causal masks. All input Q, K, and V have the same length, and the dimension is fixed at d = 64, with 12 attention heads.
They selected the same parameters in HyperAttention as mentioned earlier. As shown in Figure 4, HyperAttention achieves a 54-fold speedup without applying causal masks and a 5.4-fold speedup with them. Although the time perplexity is the same for both causal and non-causal masks, the actual algorithm for causal masks (Algorithm 1) requires additional operations, such as partitioning Q, K, and V, merging attention outputs, leading to increased actual runtime. The acceleration increases as the sequence length n grows.
The researchers believe that these results open the door to scaling self-attention not only for inference but also for training or fine-tuning LLMs to accommodate longer sequences.
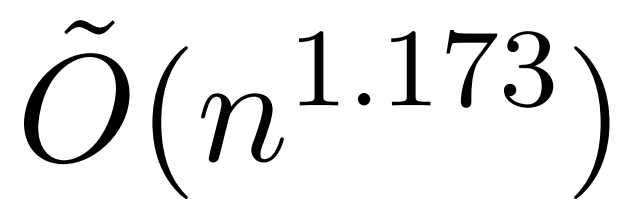 ; it employs Kernel Density Estimation (KDE) to approximate the column norms, allowing for the calculation of probabilities for sampling columns of the attention matrix.However, current KDE algorithms lack practical efficiency, and even theoretically, there is a gap between the runtime of KDEFormer and the theoretically feasible O(n) time algorithms.In this paper, the authors prove that under the same bounded entry hypothesis, a near-linear time
; it employs Kernel Density Estimation (KDE) to approximate the column norms, allowing for the calculation of probabilities for sampling columns of the attention matrix.However, current KDE algorithms lack practical efficiency, and even theoretically, there is a gap between the runtime of KDEFormer and the theoretically feasible O(n) time algorithms.In this paper, the authors prove that under the same bounded entry hypothesis, a near-linear time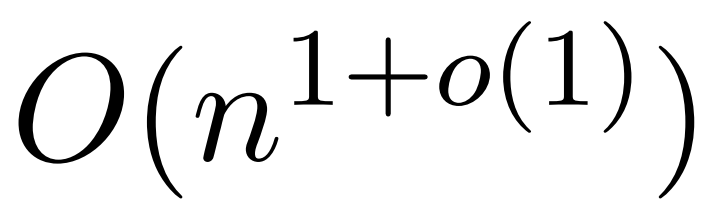 algorithm is possible.However, their algorithm also involves using polynomial methods to approximate softmax, which may not be practical.
algorithm is possible.However, their algorithm also involves using polynomial methods to approximate softmax, which may not be practical.
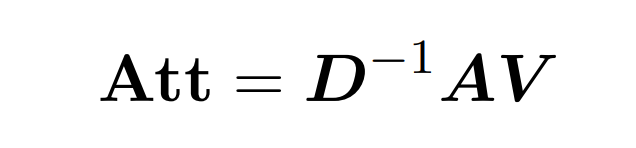
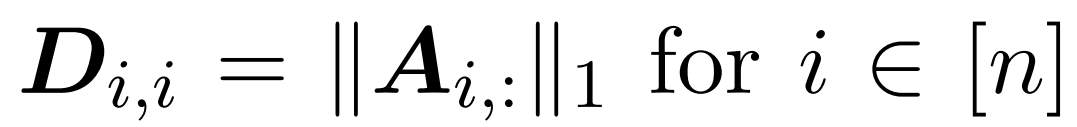 . In this case, matrix A is called the “attention matrix,” and (D^-1) A is called the “softmax matrix.” It is worth noting that directly computing the attention matrix A requires Θ(n²d) operations, and storing it consumes Θ(n²) memory.Therefore, directly computing Att requires Ω(n²d) runtime and Ω(n²) memory.
. In this case, matrix A is called the “attention matrix,” and (D^-1) A is called the “softmax matrix.” It is worth noting that directly computing the attention matrix A requires Θ(n²d) operations, and storing it consumes Θ(n²) memory.Therefore, directly computing Att requires Ω(n²d) runtime and Ω(n²) memory.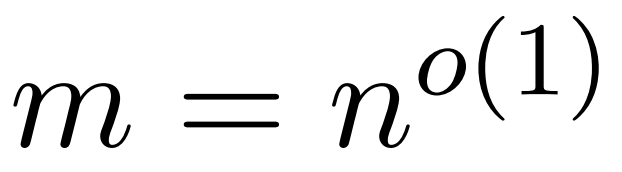 and a diagonal matrix
and a diagonal matrix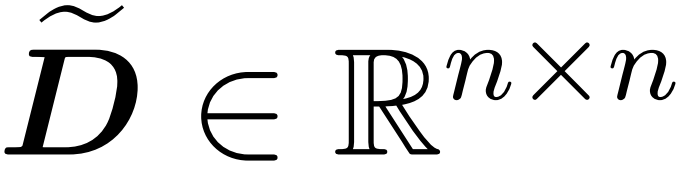 , satisfying the following constraints of the operator norm of the error:
, satisfying the following constraints of the operator norm of the error: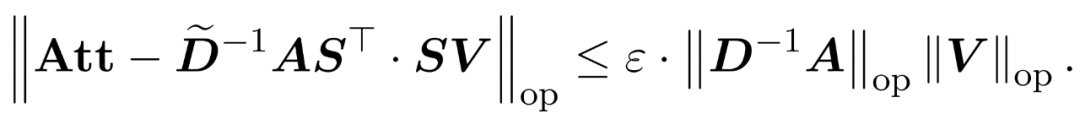

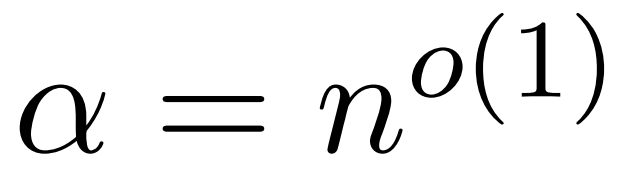 such that
such that .
.


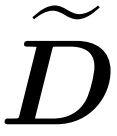 and approximating
and approximating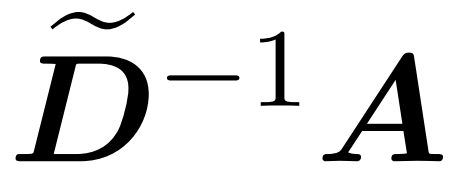 the matrix product between the value matrix V. Thus, the researchers introduce HyperAttention, an efficient algorithm that can approximate the attention mechanism with spectral guarantees in near-linear time. Algorithm 3 takes the mask MH, which defines the positions of the dominant entries in the attention matrix, as input. This mask can be generated using the sortLSH algorithm (Algorithm 1) or can be a predefined mask similar to methods in [7]. The researchers assume that the large entry mask M^H is designed to be sparse, and its number of non-zero entries is bounded
the matrix product between the value matrix V. Thus, the researchers introduce HyperAttention, an efficient algorithm that can approximate the attention mechanism with spectral guarantees in near-linear time. Algorithm 3 takes the mask MH, which defines the positions of the dominant entries in the attention matrix, as input. This mask can be generated using the sortLSH algorithm (Algorithm 1) or can be a predefined mask similar to methods in [7]. The researchers assume that the large entry mask M^H is designed to be sparse, and its number of non-zero entries is bounded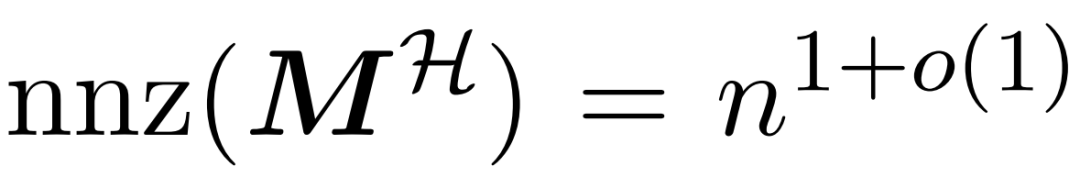 .
. and
and represent causal attention, which is only half the size of the original. To handle these causal relationships, the researchers use a recursive approach, further splitting them into smaller blocks and repeating this process. Pseudocode for this process is given in Algorithm 4.
represent causal attention, which is only half the size of the original. To handle these causal relationships, the researchers use a recursive approach, further splitting them into smaller blocks and repeating this process. Pseudocode for this process is given in Algorithm 4.



