Self-Attention Mechanism
The Self-Attention mechanism (Self-Attention)https://so.csdn.net/so/search?q=Self-Attention&spm=1001.2101.3001.7020, as a type of attention mechanism, is also known as intra Attention. It is an important component of the famous Transformer model. It allows the model to allocate weights within the same sequence, thereby focusing on different parts of the sequence to extract features. This mechanism is very effective when processing a single sequence (such as text, images, etc.) because it does not require external sequences or information to compute the attention weights.
I. Attention Mechanism
The traditional attention mechanism usually refers to how a model relies on another related sequence to determine the distribution of attention when given an input sequence.
II. Self-Attention Mechanism
The self-attention mechanism does not depend on external sequences but calculates attention weights internally within the input sequence, where each element is generated by focusing on different parts of the input sequence.
Advantages:
Flexibility: It can capture long-range dependencies without being constrained by the length of the input sequence. Parallel Computation: The computations in the self-attention layer can be executed in parallel, making it more efficient than traditional recurrent neural network structures. Interpretability: The attention maps generated by the self-attention mechanism can help explain how the model focuses on different parts of the input sequence.
Disadvantages:
Computational Cost: Although it can be processed in parallel, the computational cost and memory requirements of the self-attention mechanism increase significantly with the length of the input. Possible Overfitting: On smaller datasets, self-attention models may easily overfit due to their complexity. They require a large amount of data.
III. Self-Attention Mechanism Model Architecture
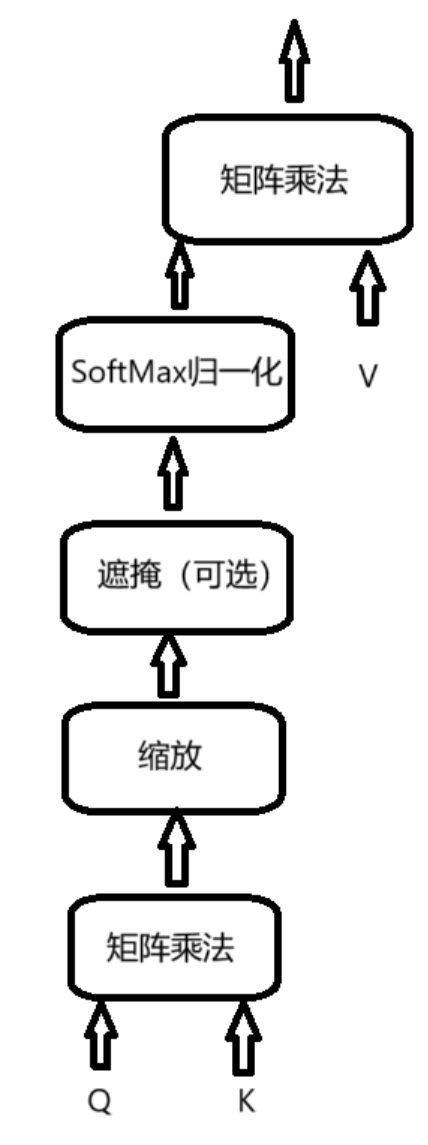
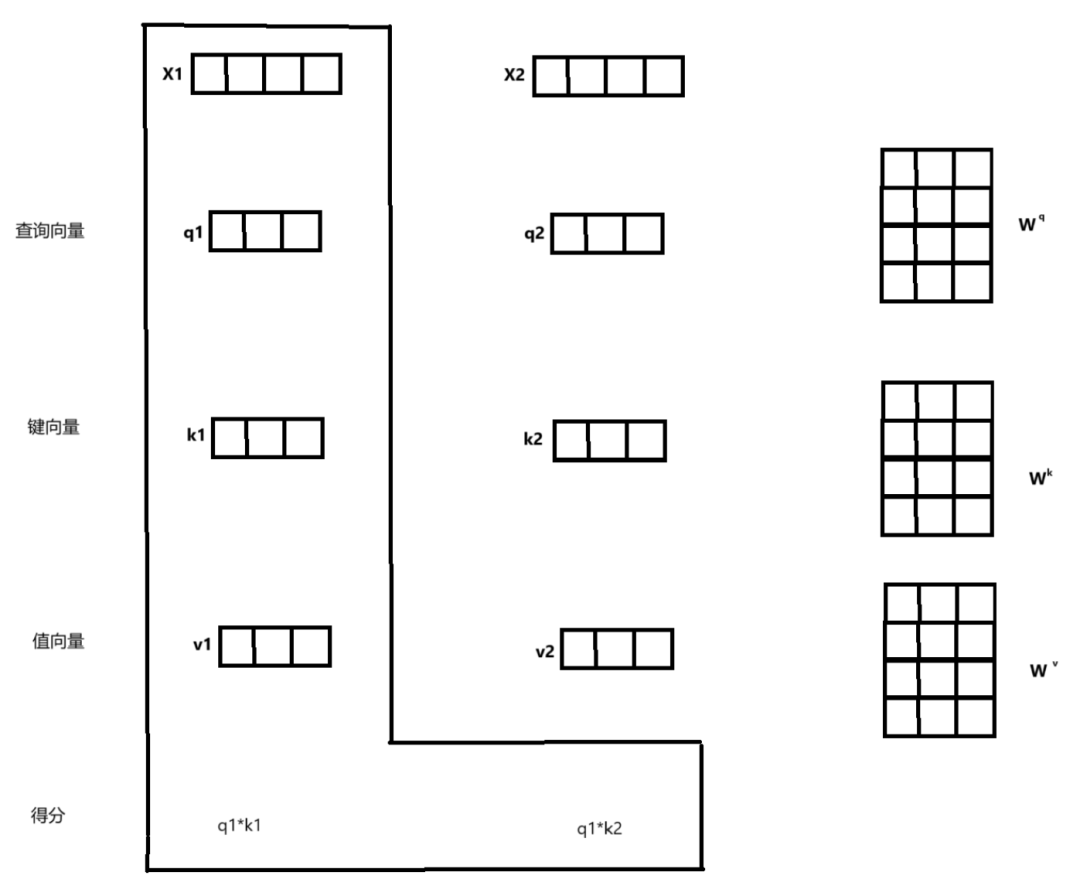
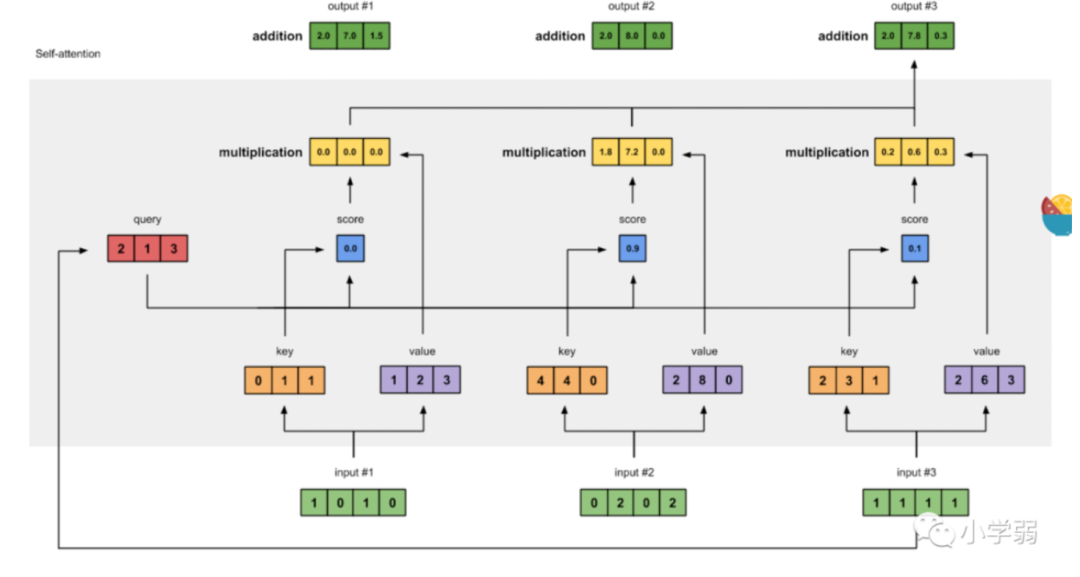
Step 1: Matrix Multiplication (MatMul) Input: Query (Q) and Key (K). Process: First, use the input word vector x to generate three new vectors q, k, and v. Each input word vector generates three new vectors. These three new vectors are called Query vector, Key vector, and Value vector, respectively. These vectors are obtained by performing a dot product between the input word vector x and three matrices. The weights of these matrices are initialized randomly and will be adjusted during training.

Calculate the dot product of the query matrix and the key matrix to measure the similarity or relevance between the query and each key. The assumption here is that certain parts of the sequence (the keys) are more relevant to the part currently being processed (the query).
In this step, we need to calculate the Score for all words based on the current word (including the current word). The value of Score determines how much attention should be placed on the corresponding other input words. In this step, the query vector and key vector must have the same dimensions for the dot product.
The dimensions of the three new vectors q, k, and v are usually smaller than the dimension of the word vector x. For example, the new vector’s dimension is 64, while the input word vector is 512. However, they do not necessarily have to be smaller than the dimension of the word vector.
Output: The result of this matrix multiplication is an attention score matrix, where each element represents the compatibility score between the query vector and the key vector.
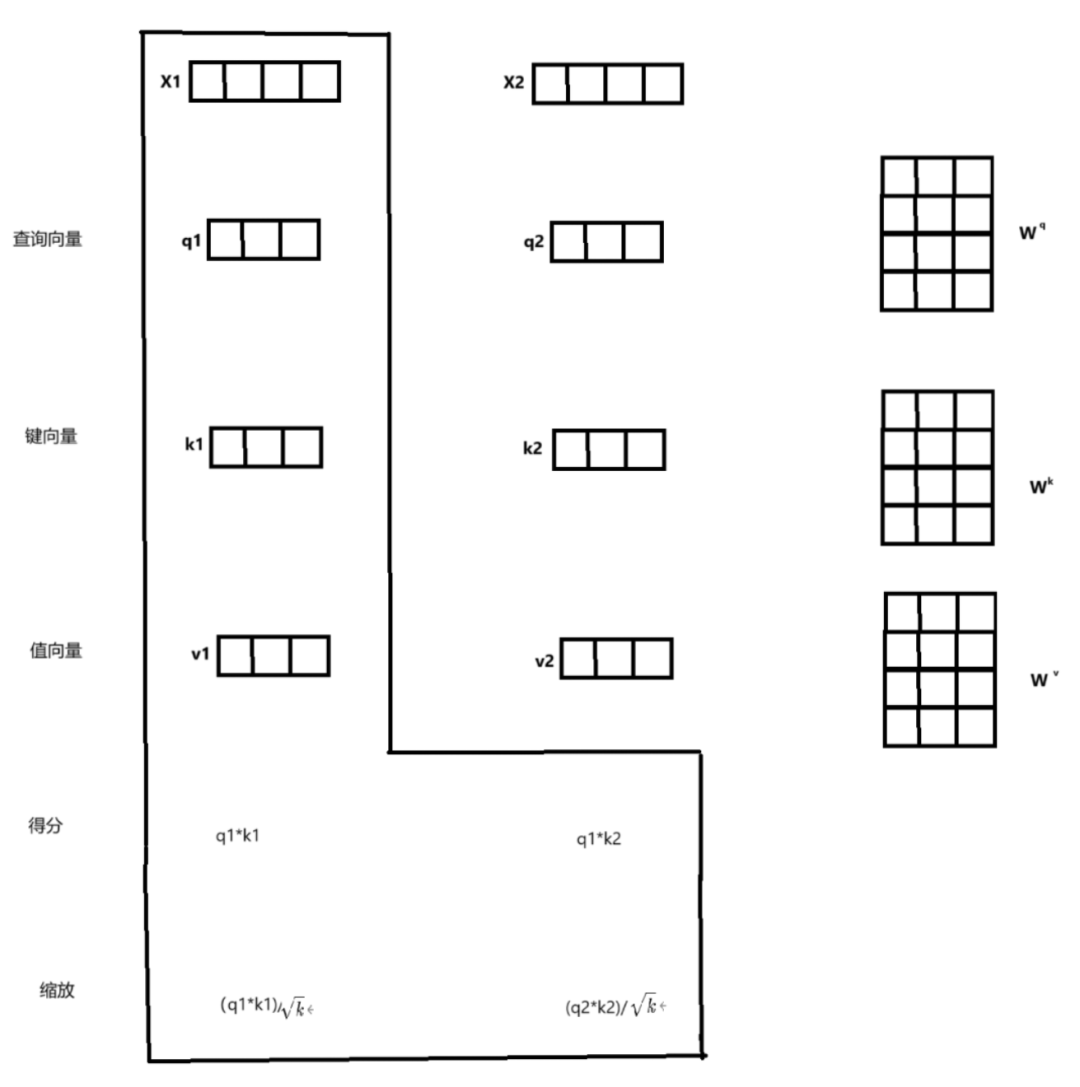
Step 2: Scaling (Scale) Input: Attention score matrix. Process: Scale the score matrix, usually by dividing by the square root of the dimension of the key vector. This scaling helps to avoid excessively large values during the softmax operation, which can lead to the vanishing gradient problem. Output: Scaled score matrix.
Step 3: Optional Masking (Mask) Input: Scaled score matrix. Process: Apply a mask, which is usually used to conceal parts of the sequence that should not be attended to. For example, in the decoder self-attention, information from future positions should be masked to prevent information leakage. Output: Masked score matrix.
Step 4: SoftMax Input: Score matrix after optional masking. Process: Use the softmax function on each row to convert scores into probabilities. This step ensures that the sum of all values in each row equals 1, representing a probability distribution. Output: Attention weights for each query against all keys.
Step 5: Matrix Multiplication (MatMul) Input: Output of Softmax (Attention Weights) and Value (V). Process: Perform matrix multiplication between the attention weight matrix and the value matrix. This step applies the computed weights to the corresponding values, which is the core of the attention mechanism. Output: The output after weighted summation, representing the input sequence’s representation considering the surrounding context.
QA
Is the output of step five a new value vector, and will the updated value vector be used again when this word appears next time?
The output of step five will participate in the calculation of Q, K, and V in the next layer, which may be further transformed or integrated. How exactly is it integrated?
In fact, during a single forward pass, the new vectors output from the self-attention layer will be used as inputs to the next layer (which may be another self-attention layer or another type of layer, such as a feedforward neural network layer). In a standard Transformer model, each self-attention layer is independent, meaning each layer recalculates new Q, K, and V vectors based on the output of the previous layer.
Therefore, if the same word (or more generally, an element in the sequence) appears multiple times in the same processing, it will recalculate its representation based on the output of the previous layer each time. This does not mean it uses the output of the previous self-attention layer directly as a