Collect! Various Amazing Self-Attention Mechanisms

Reference video can be found at:

In the transformer video of the 2021 course, Teacher Li detailed some of the self-attention content, but self-attention actually has various forms of variations:

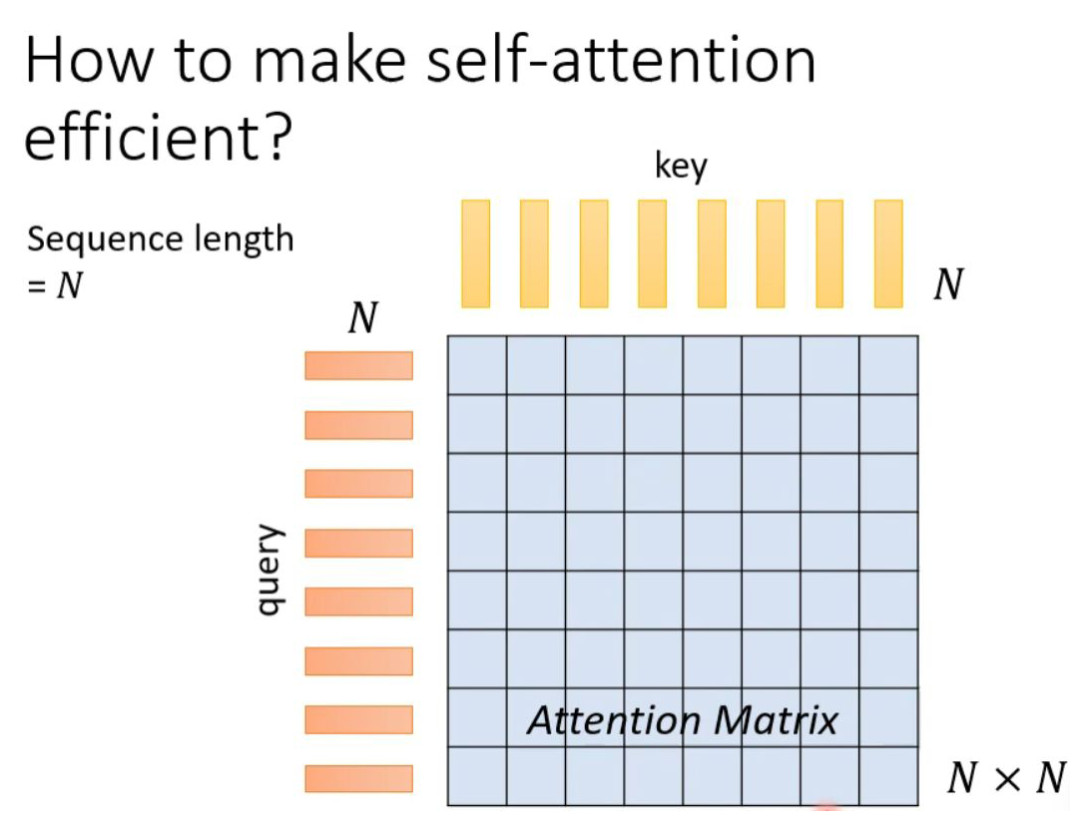
First, let’s briefly review the previous self-attention. Assuming the input sequence (query) length is N, in order to capture the relationship between each value or token, it is necessary to generate N keys corresponding to it, and by performing a dot-product between the query and key, we can produce an Attention Matrix (attention matrix) with dimensions N*N. The biggest problem with this method is that when the sequence length is too long, the corresponding Attention Matrix dimension becomes too large, causing computational difficulties.

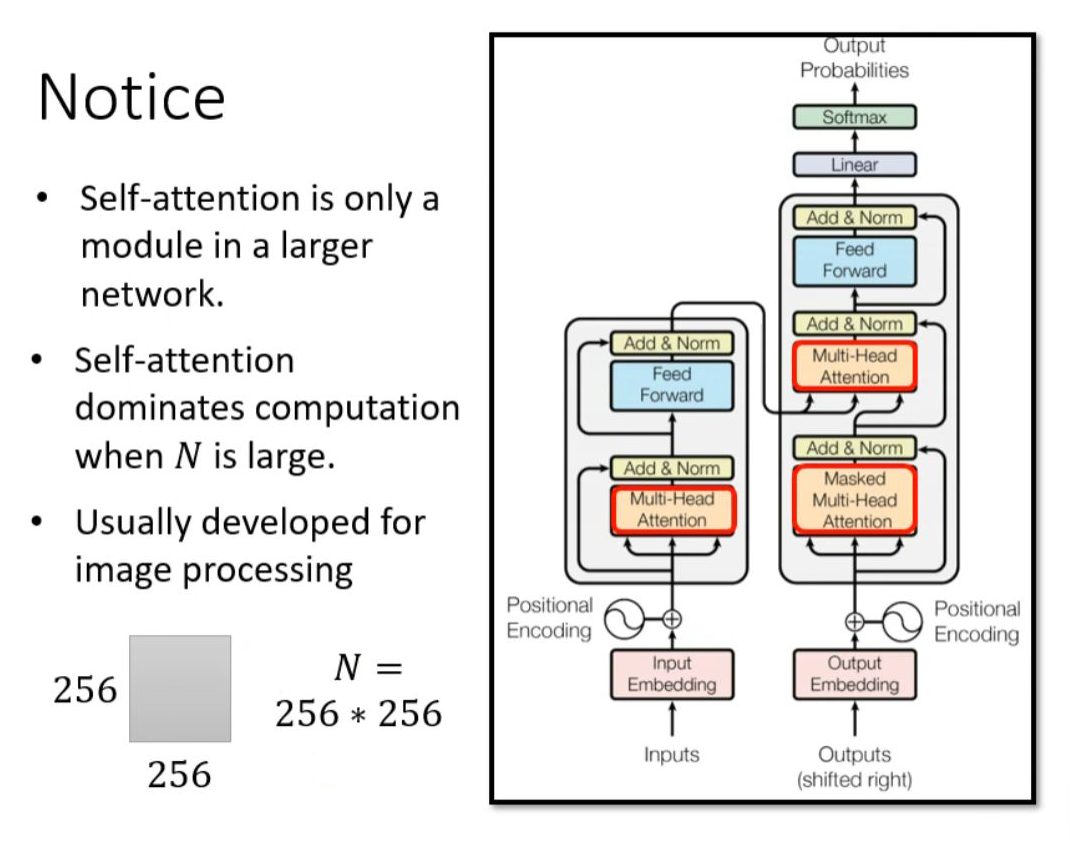
For transformers, self-attention is just one module in a large network architecture. From the above analysis, we know that the computational load for self-attention is proportional to the square of N. When N is very small, simply increasing the computational efficiency of self-attention may not significantly impact the overall network’s computational efficiency. Therefore, improving the computational efficiency of self-attention to greatly enhance the efficiency of the entire network is contingent upon N being particularly large, such as in image recognition (image processing).

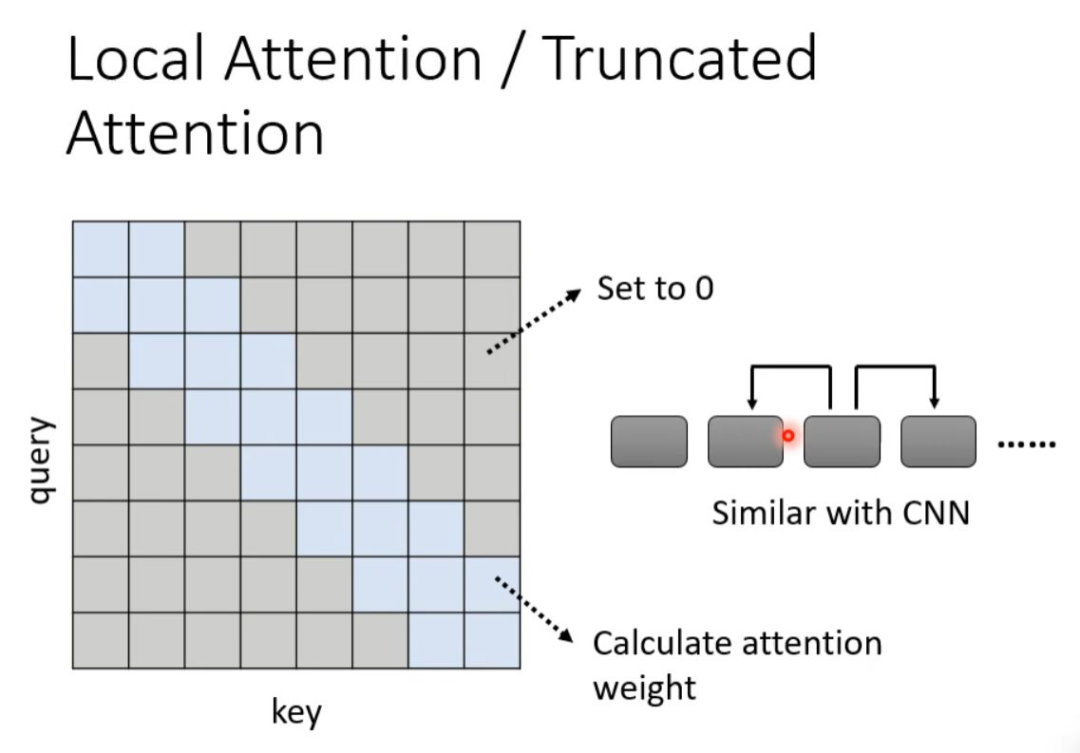
How can we speed up the computation of self-attention? Based on the above analysis, we can see that the biggest issue affecting the efficiency of self-attention is the computation of the Attention Matrix. If we can selectively compute certain values in the Attention Matrix based on some human knowledge or experience, or if we can determine some values without computation, theoretically, we can reduce the computational load and improve computational efficiency.

For example, when we are doing text translation, sometimes it is not necessary to consider the entire sequence when translating the current token; knowing just the neighboring tokens can achieve accurate translations, which is called local attention. This can significantly enhance computational efficiency, but the downside is that it only focuses on the local values, which is quite similar to CNN.

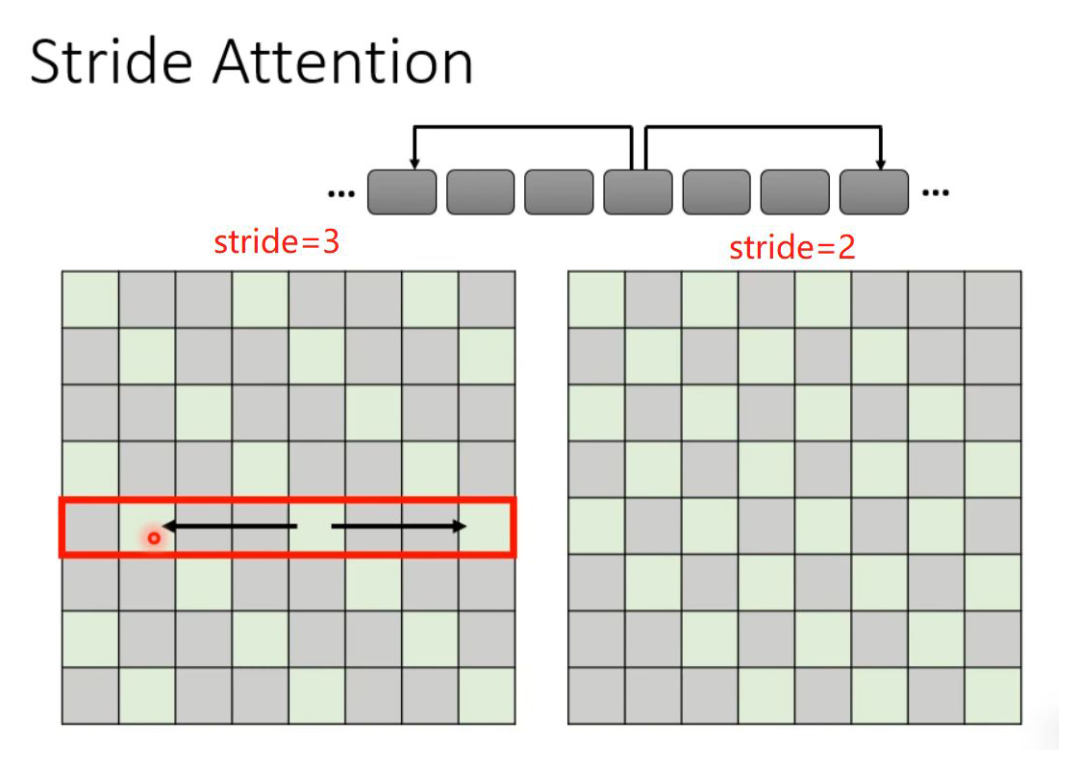
If the above local attention is not satisfactory, another approach is to give the current token a certain interval (stride) of left and right neighbors to capture the relationships between the current token and both past and future tokens. Of course, the value of stride can be determined by oneself.

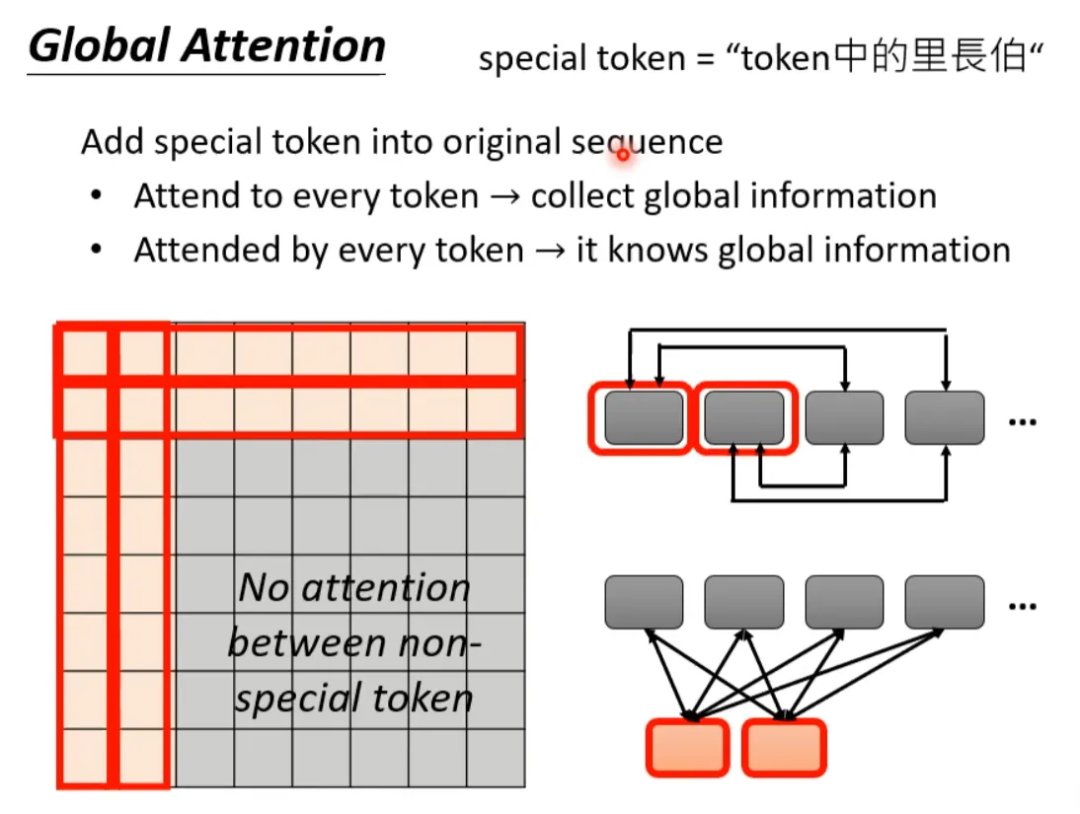
Another method is global attention, which involves selecting certain tokens in the sequence as special tokens (for example, punctuation marks), or adding special tokens to the original sequence. This allows the special tokens to establish global relationships with the sequence, while the other non-special tokens do not have attention. For instance, adding two special tokens at the beginning of the original sequence:

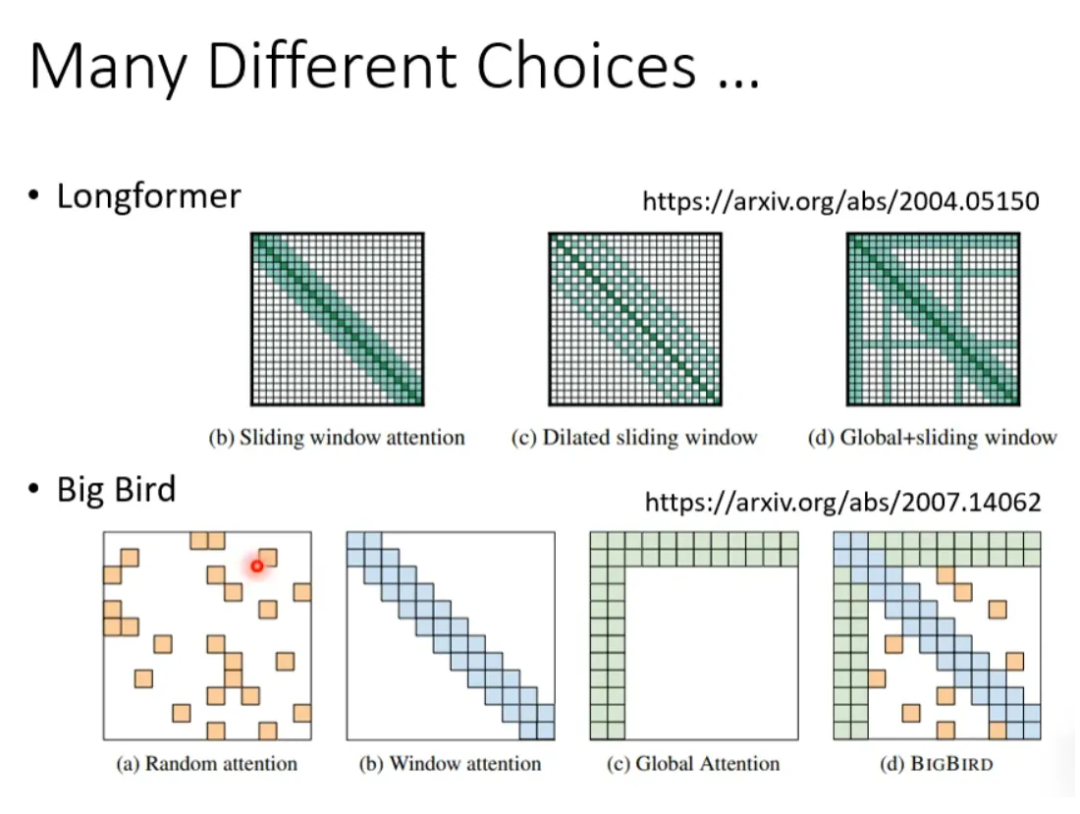
Which attention method is the best? Only children make choices… For a network, some heads can do local attention while others can do global attention… thus no choice is needed. See the following examples:

• Longformer combines the three attention methods mentioned above.
• Big Bird is based on Longformer and randomly selects attention assignments to further improve computational efficiency.

The methods mentioned above are all manually set to determine where attention needs to be calculated and where it does not. But is this the best way to calculate? Not necessarily. For the Attention Matrix, if certain position values are very small, we can directly set these positions to 0, which will not have a significant impact on the actual prediction results. In other words, we only need to identify the values in the Attention Matrix that are relatively large. But how do we find out which positions have very small/very large values?

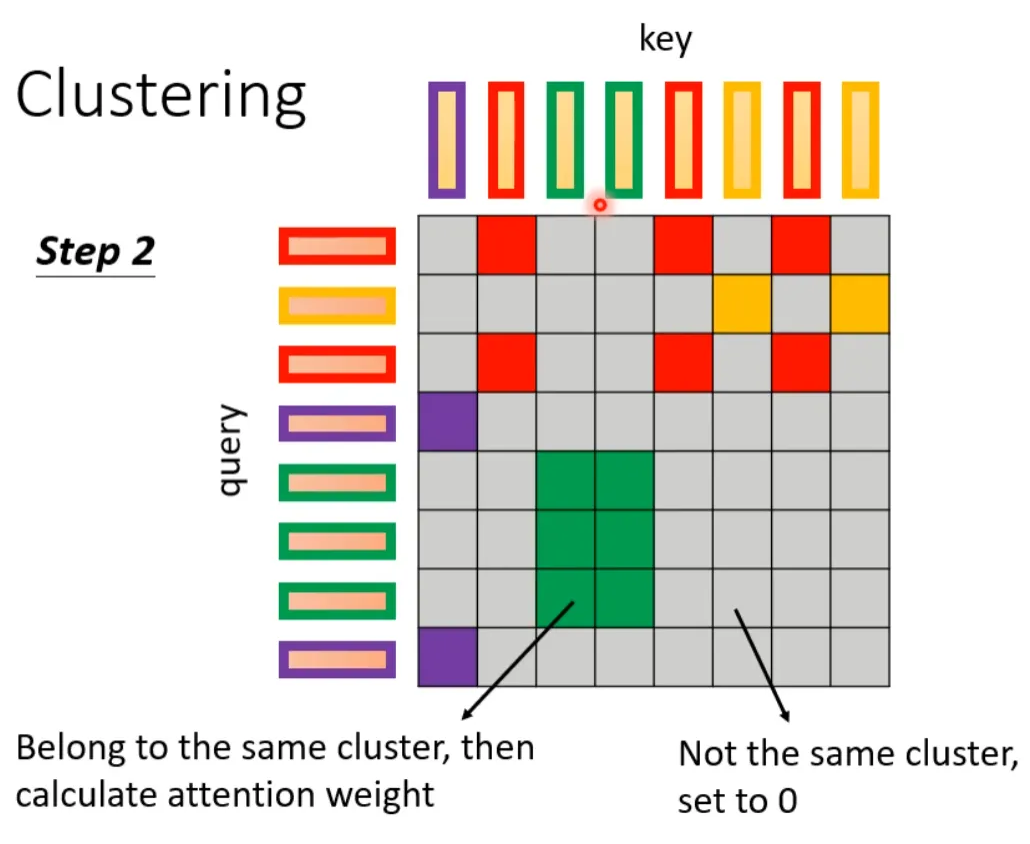
The following two papers propose a clustering scheme, which first clusters the queries and keys. Queries and keys belonging to the same class calculate attention, while those not in the same class do not participate in the calculation, thus speeding up the computation of the Attention Matrix. For example, in the following example, there are 4 classes: 1 (red box), 2 (purple box), 3 (green box), and 4 (yellow box). The two papers introduce methods for quick rough clustering.

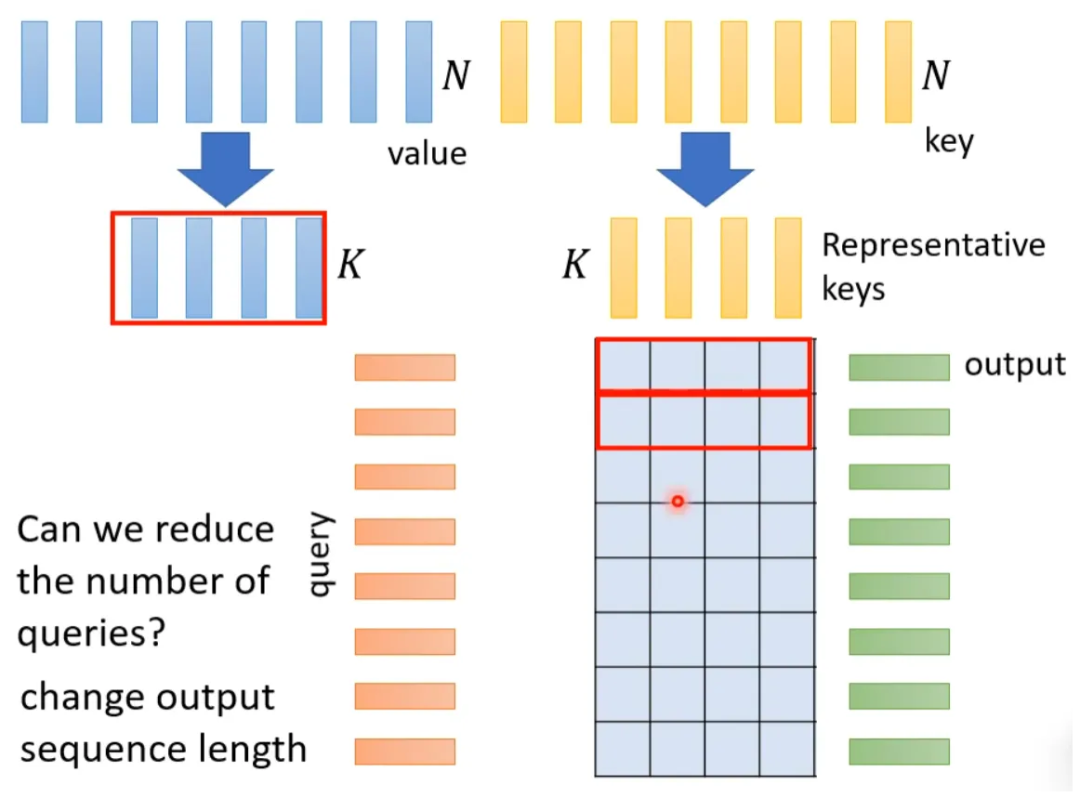
Is there a way to learn whether or not to calculate attention? It is possible. We can train another network, where the input is the input sequence and the output is a weight sequence of the same length. By concatenating all weight sequences and transforming them, we can obtain a matrix indicating where to calculate attention and where not to. One detail is that certain different sequences may output the same weight sequence through the neural network, which can greatly reduce the computational load.

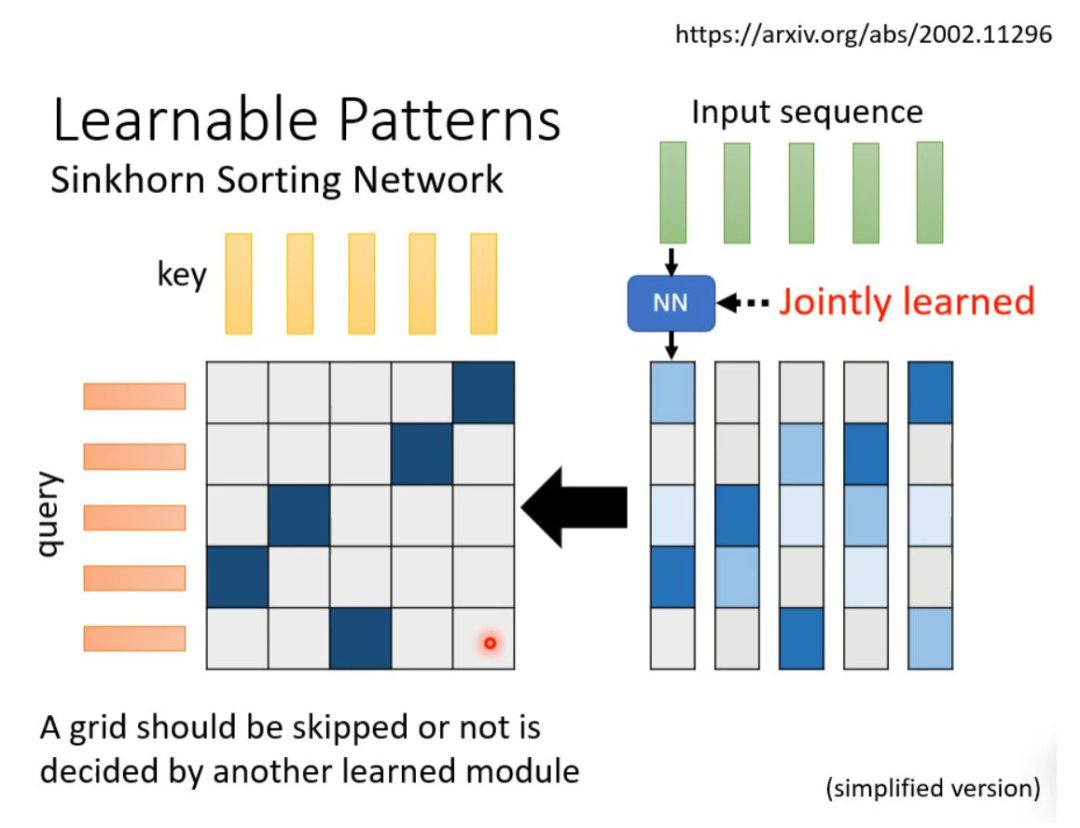
What we discussed above is the N*N matrix, but in practice, such a matrix is usually not full rank, meaning we can reduce the dimensionality of the original N*N matrix by removing redundant columns to obtain a relatively small matrix.

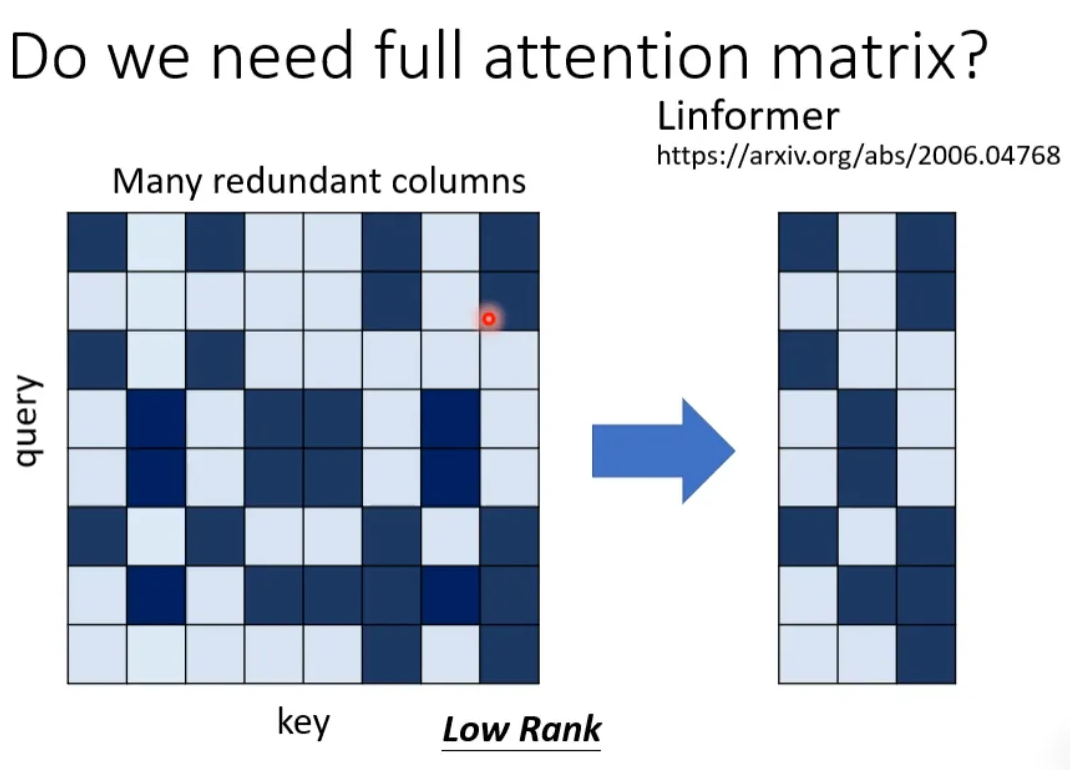
Specifically, select K representative keys from N keys, each key corresponding to a value, and then perform a dot product with the query. Then perform gradient descent to update the value.

Why select representative keys instead of representative queries? Because queries correspond to outputs, thus the output would be shortened, resulting in loss of information.

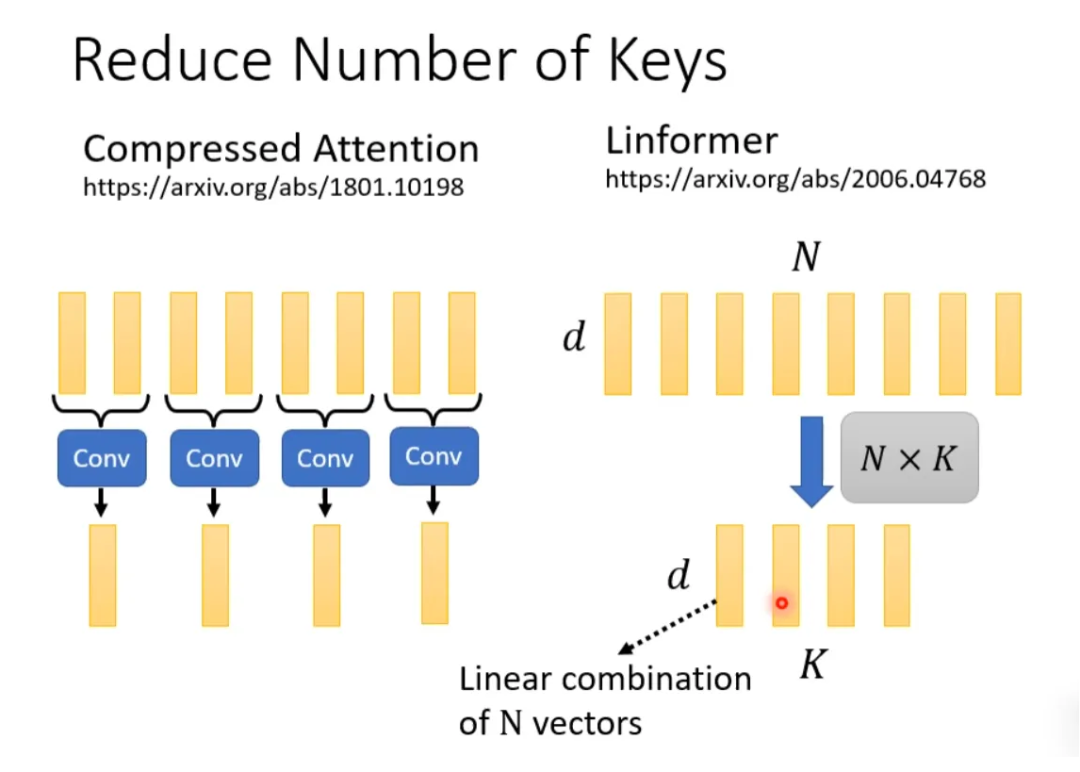
How to select representative keys? Here are two methods: one is to directly convolve (conv) the keys, and the other is to perform matrix multiplication with a matrix.

Let’s review the computation process of the attention mechanism, where I is the input matrix and O is the output matrix.

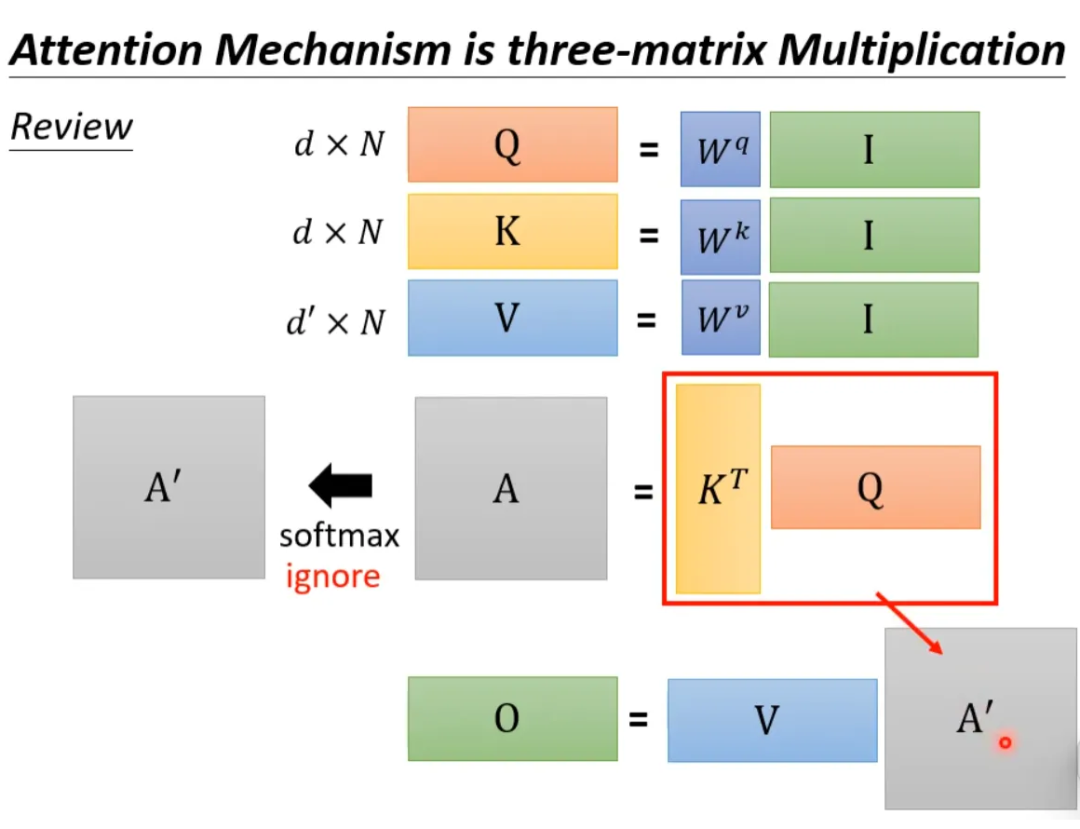
First, ignore softmax, and it can be expressed in the following form:

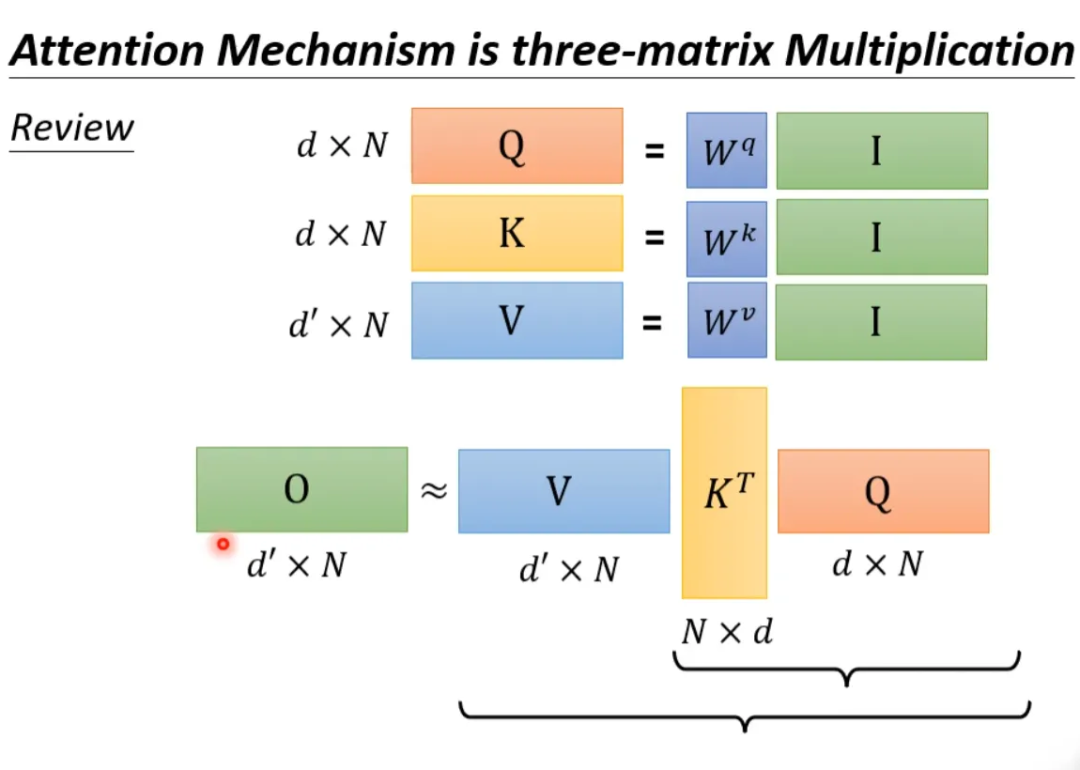
The above process can be accelerated. If we compute V*K^T first and then multiply by Q, it will yield the same result as K^T*Q multiplied by V, but the computational load will be significantly reduced.

Appendix: Linear algebra explanation regarding this part

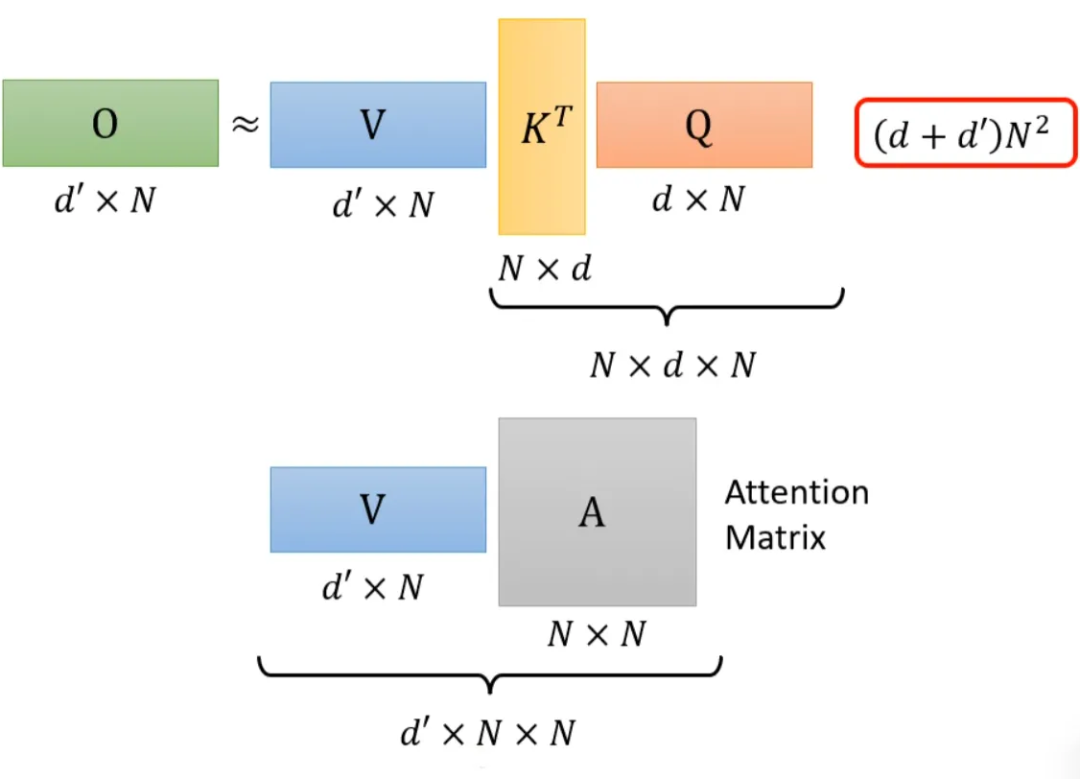
Still explaining the above example. If we compute K^T*Q, it will execute N*d*N multiplications. V*A will execute d’*N*N multiplications, so the total computational load is (d+d’)N^2.

If we compute V*K^T, it will execute d’*N*d multiplications. Then multiplying by Q will execute d’*d*N multiplications, so the total computational load is 2*d’*d*N.

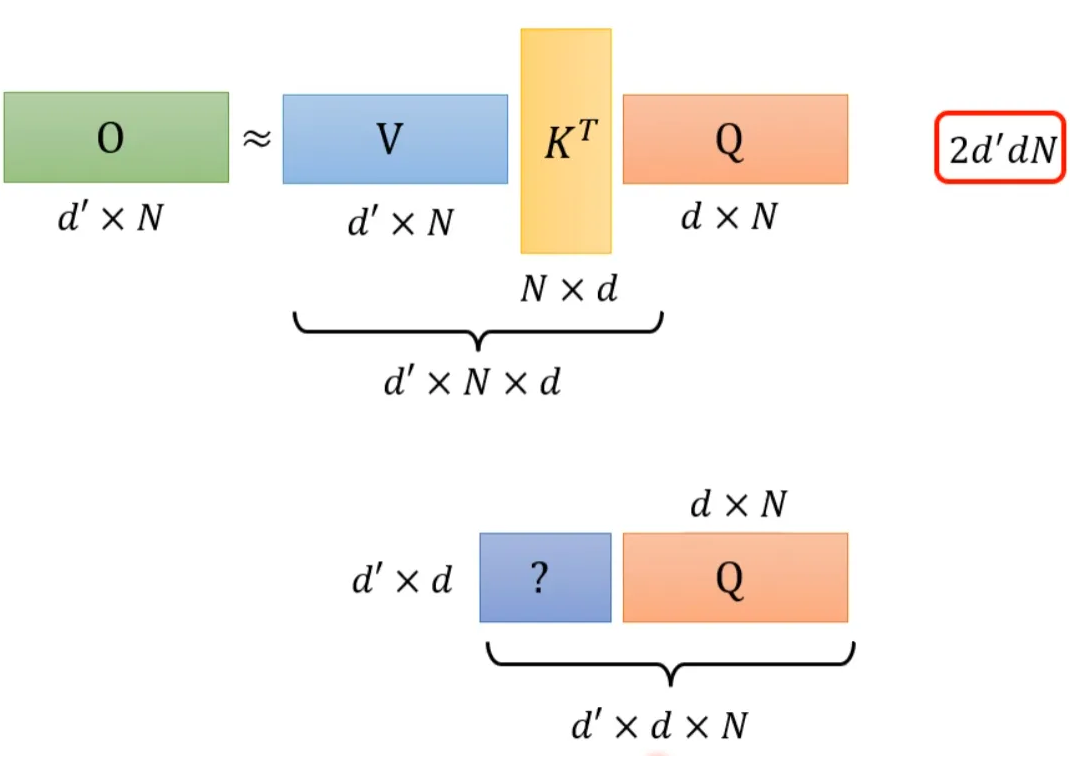
And (d+d’)N^2>>2*d’*d*N, so by changing the order of operations, we can greatly enhance computational efficiency.

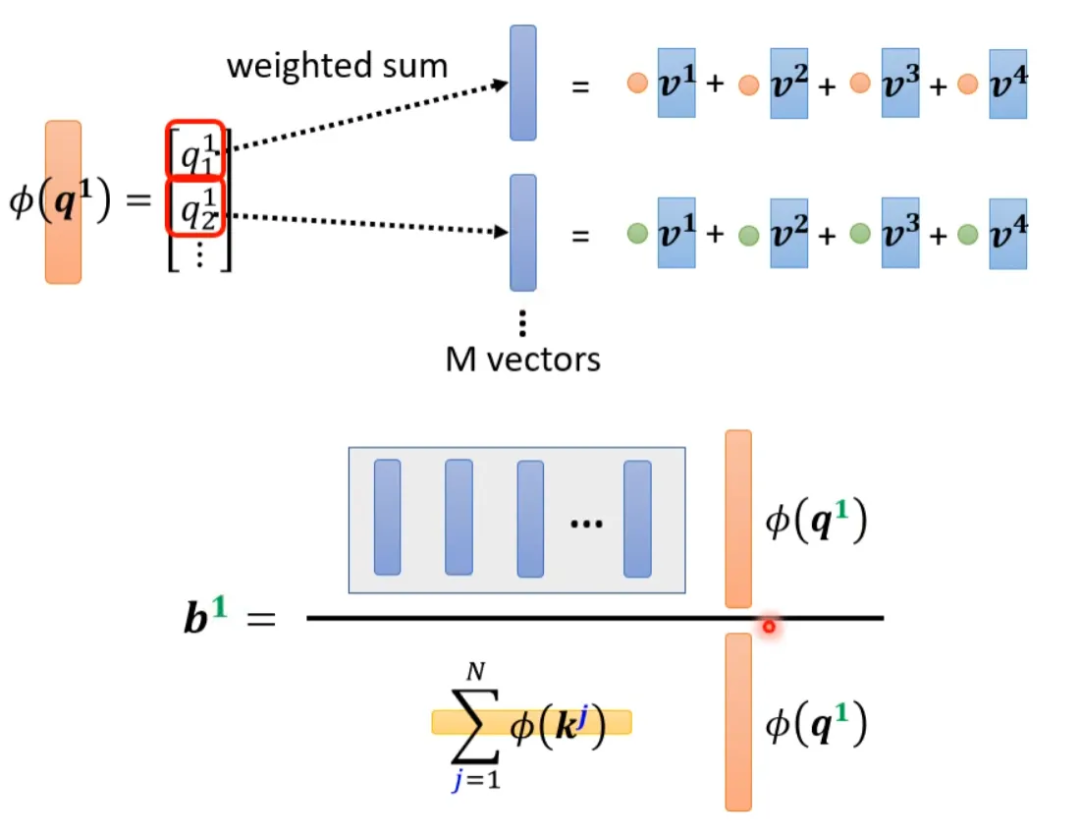
Now let’s bring back softmax. The original self-attention looks like this, taking b1 as an example:

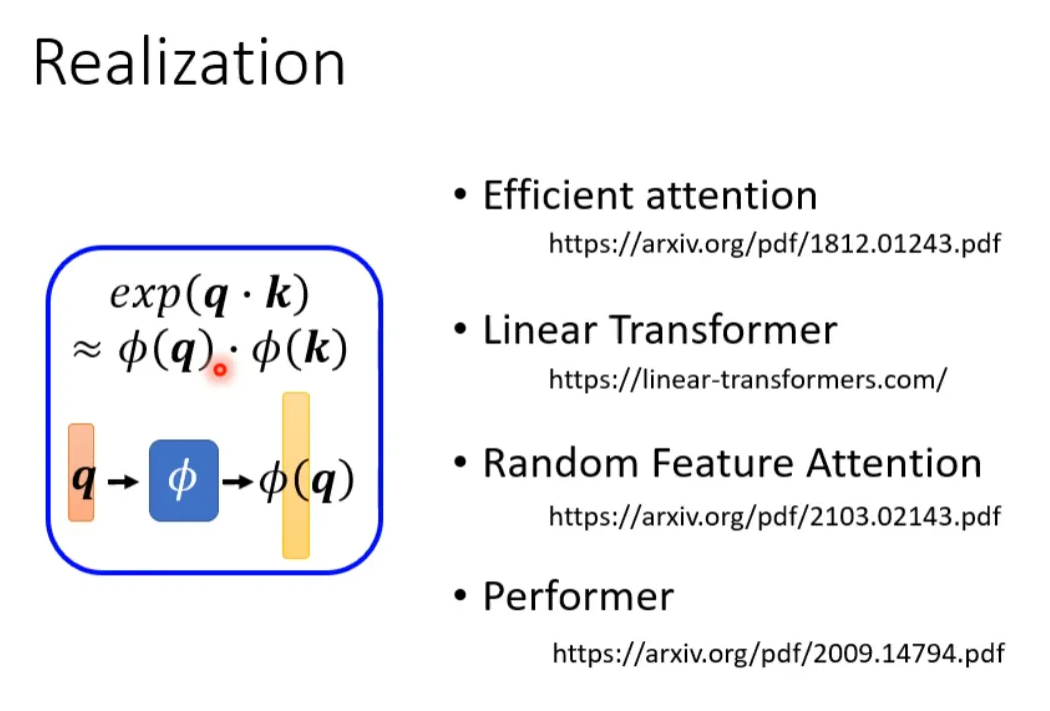
If we can convert exp(q*k) into the form of two mappings multiplied, we can further simplify the above formula:

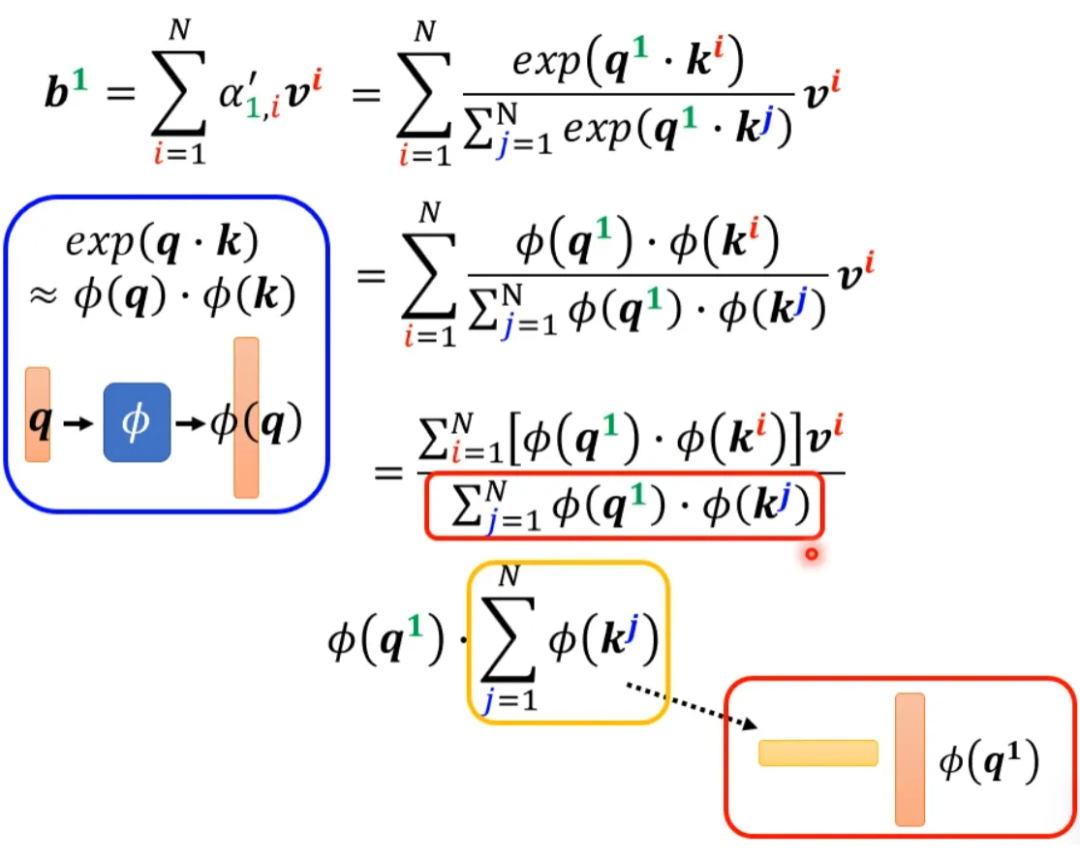
▲ Simplification of the denominator

▲ Simplification of the numerator

Taking the items inside the parentheses as a vector, M vectors form an M-dimensional matrix, which, when multiplied by φ(q1), yields the numerator.

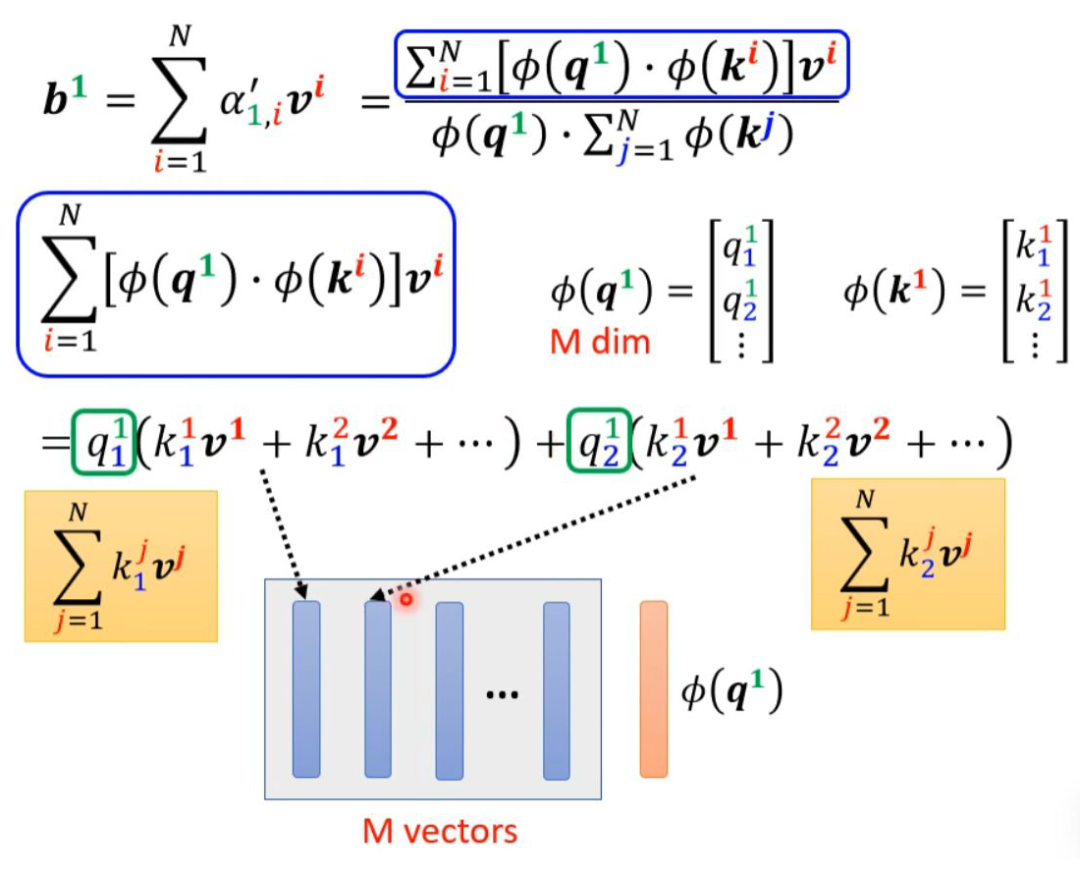
Graphically represented as follows:

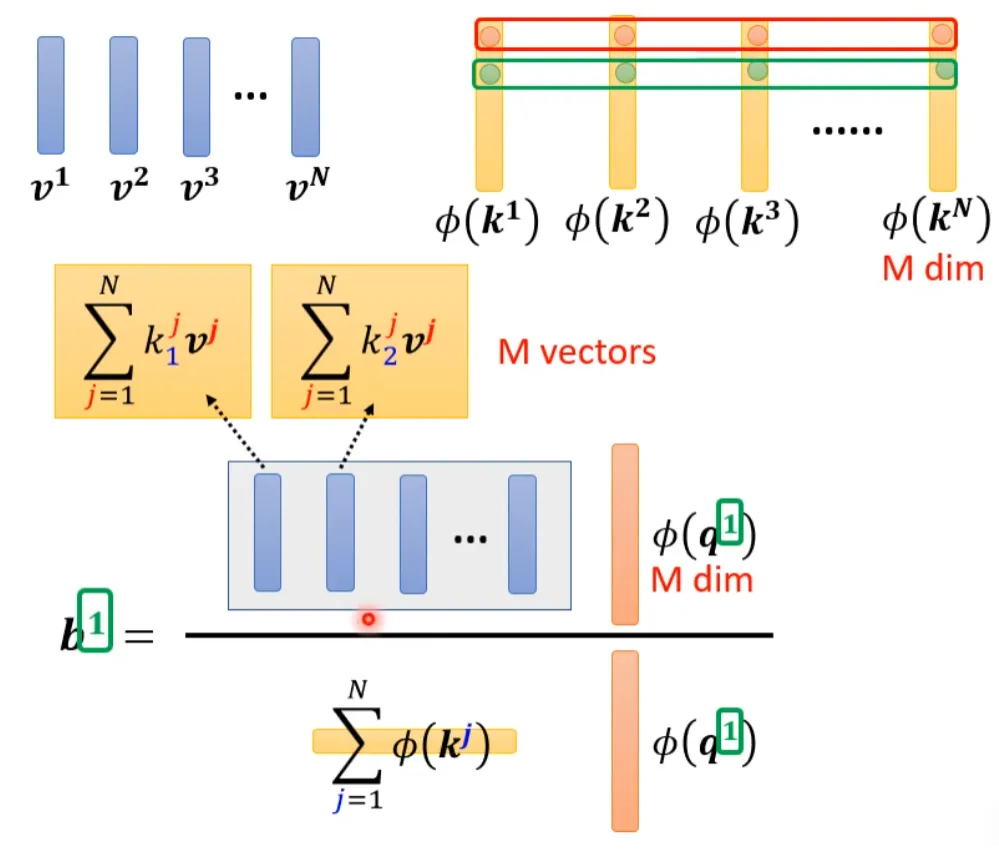
From the above, it can be seen that the blue vector and the yellow vector are actually unrelated to the 1 in b1. This means that when we compute b2, b3…, the blue and yellow vectors do not need to be recalculated.

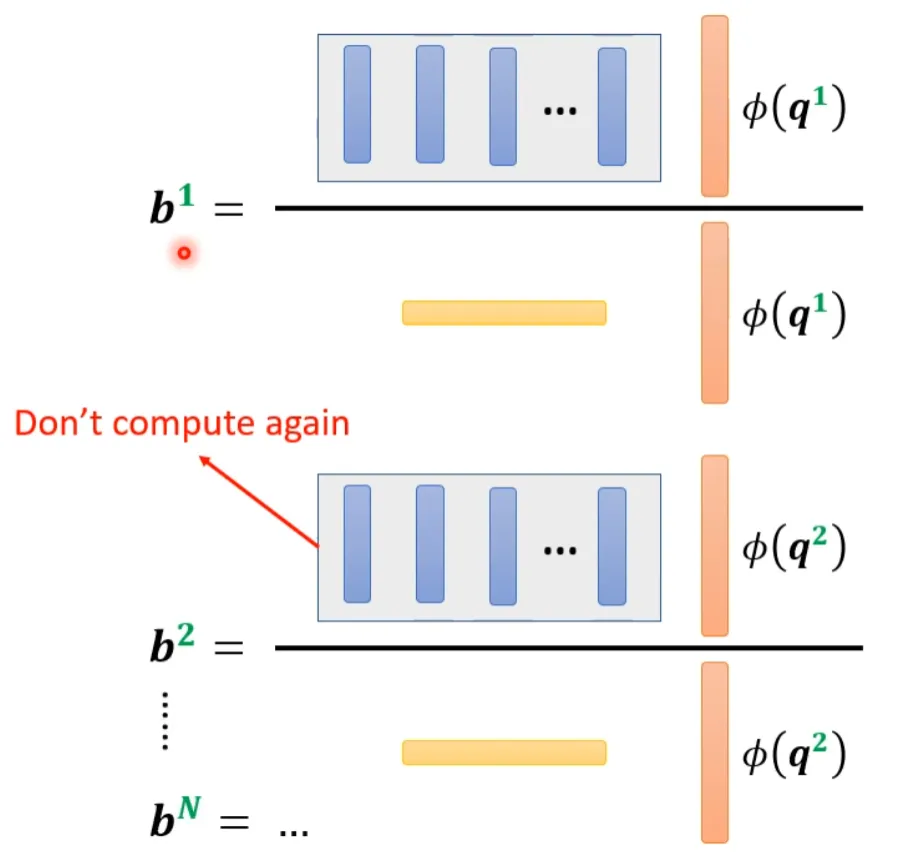
Self-attention can also be viewed in another way. This computation method is almost identical to the results produced by the original self-attention but significantly reduces the computational load. Simply put, first find a transformation φ(), transform k, and then perform a dot product with v to obtain an M-dimensional vector. Then transform q and multiply it with the corresponding dimension of M. The M-dimensional vector only needs to be computed once.

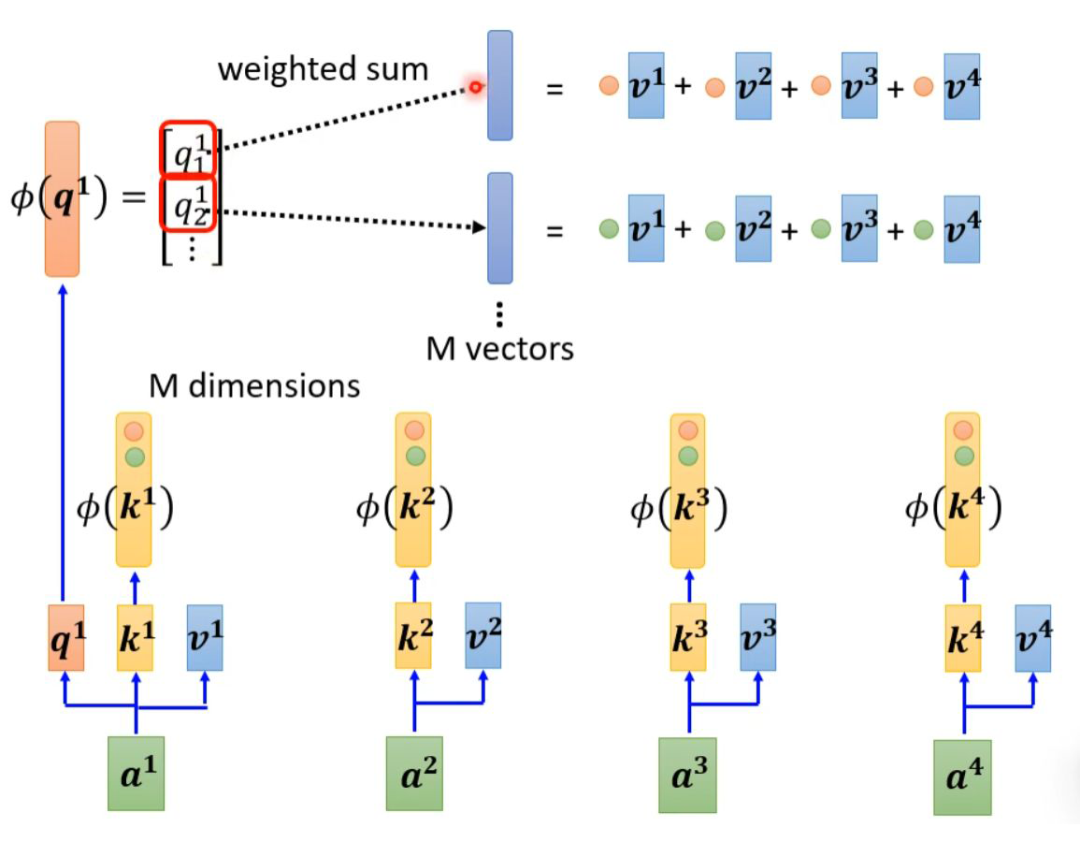
b1 is computed as follows:

b2 is computed as follows:

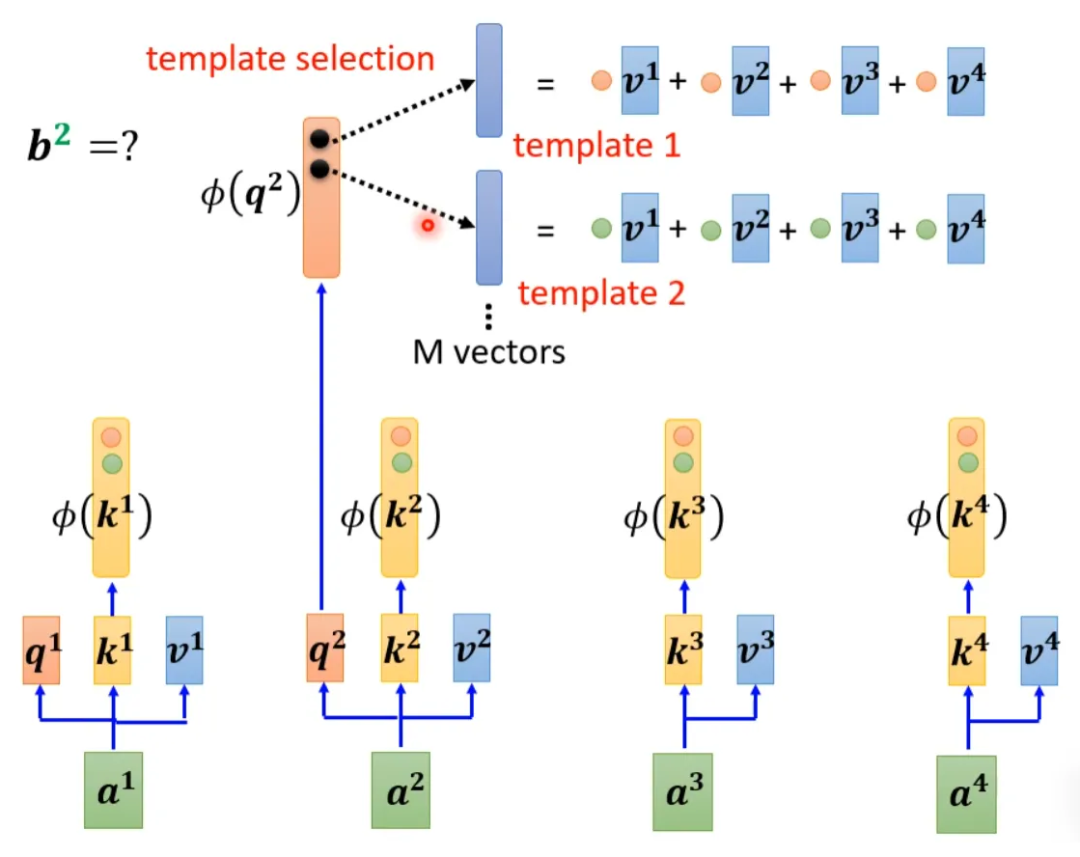
This can be understood as treating φ(k) and v to compute the vector as a template, and then using φ(q) to find which template is the most important and perform matrix operations to obtain the output b.

So how to choose φ? Different literature has different methods:

Do we necessarily need q and k when calculating self-attention? Not necessarily. In the Synthesizer literature, the attention matrix is not obtained through q and k, but learned as network parameters. Although different input sequences correspond to the same attention weights, performance does not deteriorate significantly. This also raises a question: what is the value of attention?

Is it necessary to use attention to process sequences? Is it possible to try discarding attention? Are there attention-free methods? Below are several MLP methods used as alternatives to attention for processing sequences.

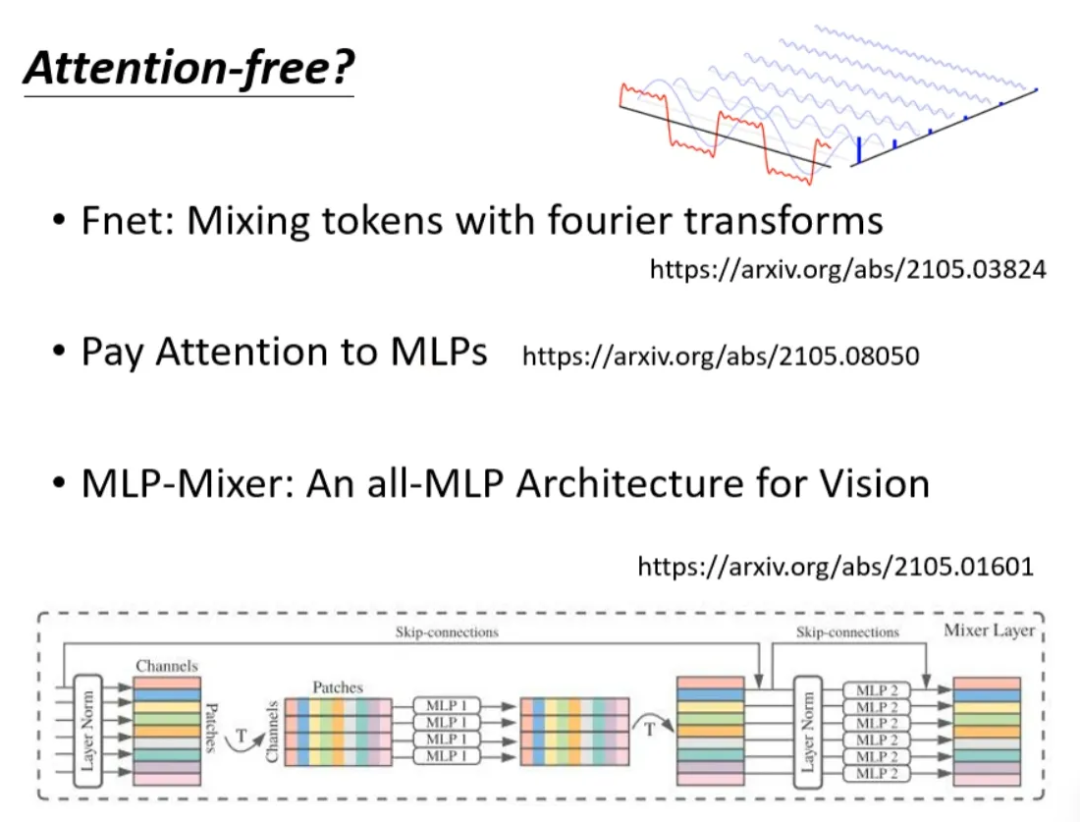
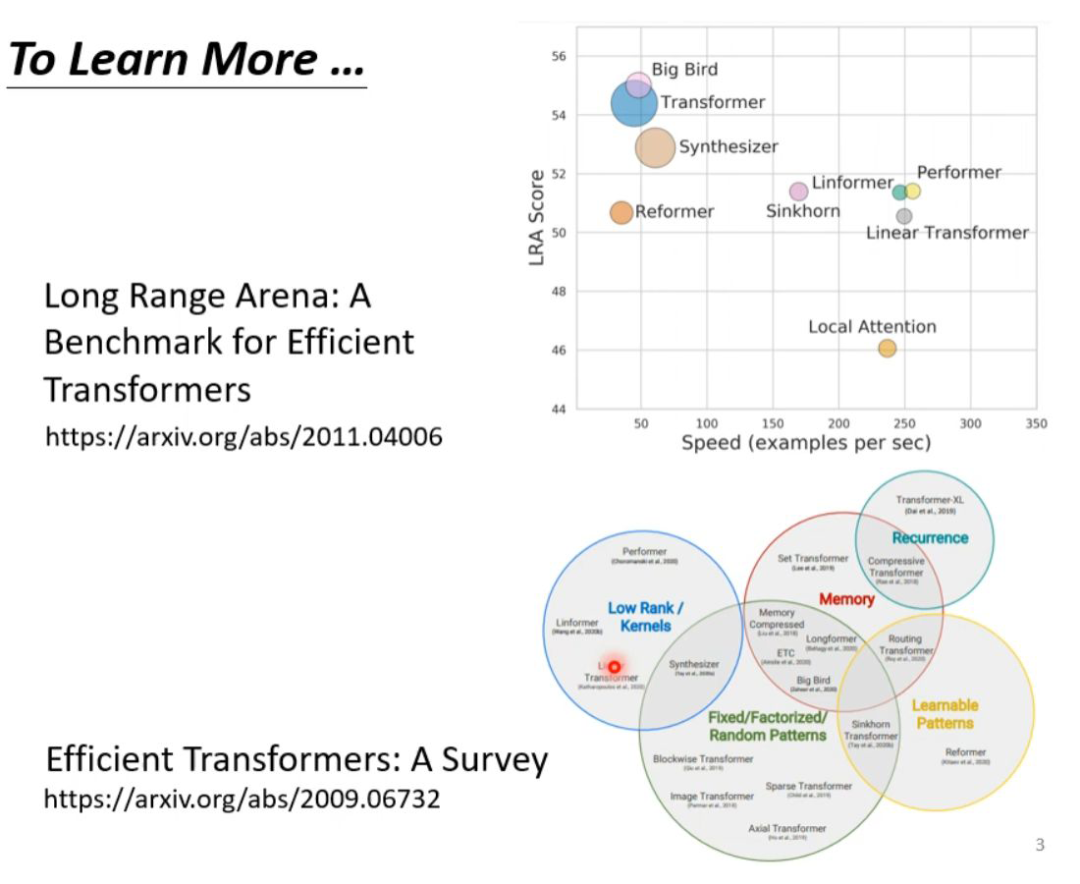
The last page summarizes all the methods discussed today. In the figure below, the vertical axis represents the LRA score, where higher values indicate better network performance; the horizontal axis indicates how many sequences can be processed per second, with further right indicating faster speed; larger circles represent more memory used (greater computational load).

That concludes Teacher Li’s summary of “Various Amazing Self-Attention Mechanisms” for this class.

Download 1: OpenCV-Contrib Extension Module Chinese Tutorial

Reply in the "Beginner Learning Vision" public account backend: Extension Module Chinese Tutorial to download the first OpenCV extension module tutorial in Chinese, covering installation of extension modules, SFM algorithms, stereo vision, object tracking, biological vision, super-resolution processing, and more than twenty chapters of content.

Download 2: Python Vision Practical Project 52 Lectures

Reply in the "Beginner Learning Vision" public account backend: Python Vision Practical Project to download 31 visual practical projects including image segmentation, mask detection, lane line detection, vehicle counting, eyeliner addition, license plate recognition, character recognition, emotion detection, text content extraction, facial recognition, etc., to help quickly learn computer vision.

Download 3: OpenCV Practical Project 20 Lectures

Reply in the "Beginner Learning Vision" public account backend: OpenCV Practical Project 20 Lectures to download 20 practical projects based on OpenCV for advanced learning of OpenCV.

Discussion Group

Welcome to join the public account reader group to communicate with peers. Currently, there are WeChat groups for SLAM, 3D vision, sensors, autonomous driving, computational photography, detection, segmentation, recognition, medical imaging, GAN, algorithm competitions, etc. (which will gradually be subdivided). Please scan the WeChat number below to join the group, and note: "Nickname + School/Company + Research Direction", for example: "Zhang San + Shanghai Jiao Tong University + Visual SLAM". Please follow the format for remarks, otherwise, you will not be approved. After successful addition, you will be invited to join the relevant WeChat group based on your research direction. Please do not send advertisements in the group, or you will be removed from the group. Thank you for your understanding~