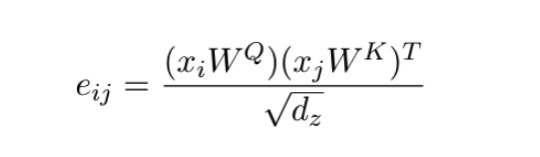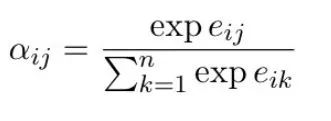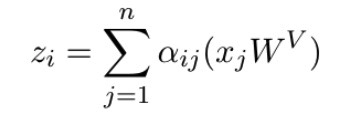Click on the "Xiaobai Learns Vision" above, select "Star" or "Pin"
Heavy content delivered first
This article is compiled from Zhihu Q&A, used for academic sharing only, copyright belongs to the author. If there is any infringement, please contact the backend for deletion.
Author | Guohao Li
https://www.zhihu.com/question/366088445/answer/1023290162
Let’s talk about my understanding.
First, the conclusion is that most GCNs and Self-attention belong to Message Passing. The Message in GCN is propagated from the neighboring nodes of a node, while the Message in Self-attention is propagated from the Query’s Key-Value.
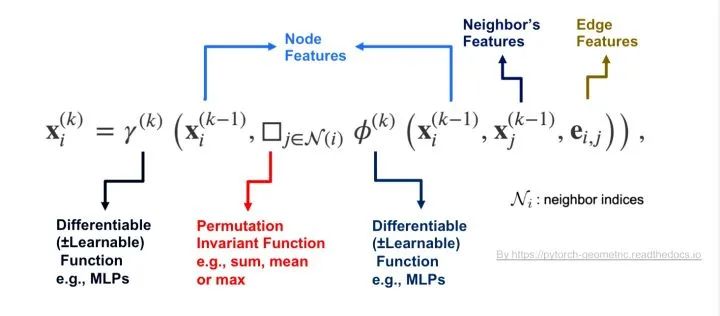
First, let’s see what Message Passing is. We know that when implementing and designing GCNs, many times a Message Passing framework is adopted, whose idea is to transmit the feature information of each node’s neighborhood to the node. Here’s an example describing the process of a node i in the k-th layer of GCN convolution:
1) Each neighbor j of node i forms a Message after the feature of that node is transformed by a function (corresponding to the operation in the formula inside function \phi);
2) A Permutation Invariant function aggregates all Messages from the neighborhood of that node (corresponding to function \square);
3) The aggregated neighborhood information and node features are then transformed by function \gamma to obtain the features X_i of that node after the k-th layer of graph convolution.
So, does Self-attention also fall within the Message Passing framework? Let’s first review how Self-attention is generally computed, here’s an example of a Query i’s attention computation process:
1) The feature x_i of Query i will calculate a similarity e_ij with each Key j’s feature;
2) After obtaining the similarity of Query i with all Keys, it goes through SoftMax to get the Attention coefficient \alpha_ij;
3) The output z_j of Query i is calculated by weighting Value j with the Attention coefficient.
Now, let’s look at their correspondence. The conclusion is that steps 1), 2) in Self-attention correspond to steps 1), 2) in Message Passing.
If we use Message Passing to implement Self-attention, we can correspond them as follows:
-1 Each Key-Value j can be seen as a neighbor of Query i;
-2 The calculation of similarity and Attention coefficient, and the operation of multiplying Value j by the Attention coefficient can correspond to the process of forming a Message in Message Passing;
-3 Finally, the summation operation in Self-attention corresponds to the Permutation Invariant function in Message Passing, meaning that the aggregation of neighborhood information here is achieved through Query’s aggregation of Key-Value.
In other words, the Attention process connects each Query with all Keys to form a Complete Bipartite Graph (Query on the left, Key-Value on the right), and then performs Message Passing on this graph for all Query nodes. Of course, Self-attention, where Query and Key-Value are the same, is just performing Message Passing on a general Complete Graph.
At this point, you might wonder why there is no third step in Message Passing that transforms the aggregated information and node information through the \gamma function in Self-attention. Yes, without this step, it is likely that the original features of the Query would be lost during the learning process. In fact, this step is still present in “Attention is All You Need”; if you don’t believe it, take a look:
After each Self-Attention, there is basically a Skip connection + MLP, which to some extent corresponds to the \gamma function in Message Passing, doesn’t it?
So, to put it simply, both GCN and Self-attention fall within the Message Passing framework. The Message in GCN is propagated from the neighboring nodes of the node, while the Message in Self-attention is propagated from the Query’s Key-Value. If we call all Message Passing functions GCN, then Self-attention is a special case of GCN acting on the Complete Graph formed by Query and Key-Value. Just as Naiyan Wang’s answer indicates.
It can be said that GCN in NLP should have great potential, as Self-attention can be seen as a type of GCN, thus there must exist GCNs with stronger expressive power and broader applicability than Self-attention.
Thanks to @Ye Zihao for the supplementary information in the comments, the DGL team has written a detailed tutorial on implementing Transformer with Message Passing. Those interested in specific implementations can read it: DGL Transformer Tutorial.
1. Attention is All You Need
2. Self-Attention with Relative Position Representations
4. DeepGCNs for Representation Learning on Graphs
Author | Houye
https://www.zhihu.com/question/366088445/answer/1022692208
Let’s talk about my understanding.
The Attention in GAT is self-attention, as stated by the author in the paper.
Next, let’s discuss my understanding:
GNNs, including GCNs, are neural network models that aggregate neighbor information to update node representations. The following diagram from GraphSAGE illustrates the aggregation process well. Here we focus only on Figure 2: The red point u is the point we ultimately need to focus on, and the three blue points {v1,v2,v3} are the first-order neighbors of the red point. Every time the representation of the red node is updated, GNN collects information from the three blue points and aggregates it, then updates the representation of the red node through a neural network. The neural network can be a mean-pooling, where the weights for v1, v2, and v3 are all 1/3.
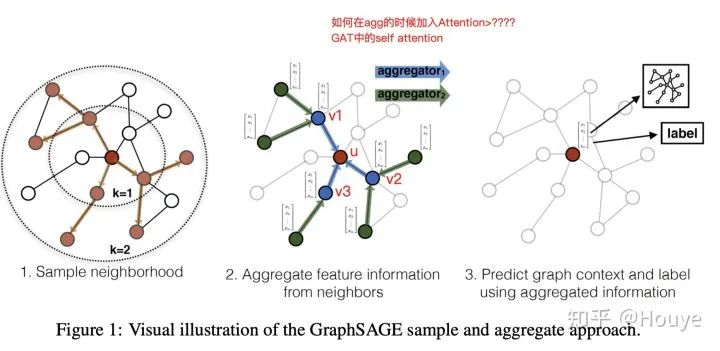Now, there’s a problem: all three blue points are neighbors, and intuitively, different neighbors have different importance for the red point. So, can we consider the importance of neighbors to weight the aggregation when GNN aggregates neighbors (e.g., 0.8v1 + 0.19v2 + 0.01v3)? Manual weighting is certainly impractical. Although weighting seems better, GNN can still perform without weighting; in some datasets, the performance without weighting can even be better.
Personally, I feel that in deep learning, “weighting = attention”. Here we can design an attention mechanism to achieve weighting of neighbors. The weights can be understood as edge weights, which are specific to a pair of nodes (e.g., u and v1).
Now, why is it self-attention? Because GNN considers itself as a neighbor during aggregation. That is, the neighbor set of u in the above diagram is actually {u,v1,v2,v3}. This is quite natural, as the information from neighbors can only be supplementary; the information from the node itself is the most important.
The problem now transforms to: Given {u,v1,v2,v3} as input, how to better represent u? This is quite similar to self-attention in NLP, as shown in the following diagram (from Chuan Tuo Scholar: Detailed Explanation of Attention Mechanism (II) — Self-Attention and Transformer).
Finally, to summarize: GCNs, self-attention, and even attention do not have a necessary connection. Weighting neighbors to learn better node representations is an optional choice.
Good news!
Xiaobai Learns Vision Knowledge Circle
Has started to open to the outside👇👇👇
Download 1: OpenCV-Contrib Extension Module Chinese Version Tutorial
Reply "Extension Module Chinese Tutorial" in the backend of the "Xiaobai Learns Vision" public account to download the first OpenCV extension module tutorial in Chinese, covering installation of extension modules, SFM algorithms, stereo vision, object tracking, biological vision, super-resolution processing, and more than twenty chapters of content.
Download 2: Python Vision Practical Projects 52 Lectures
Reply "Python Vision Practical Projects" in the backend of the "Xiaobai Learns Vision" public account to download 31 practical vision projects including image segmentation, mask detection, lane detection, vehicle counting, eyeliner addition, license plate recognition, character recognition, emotion detection, text content extraction, facial recognition, etc., to help quickly learn computer vision.
Download 3: OpenCV Practical Projects 20 Lectures
Reply "OpenCV Practical Projects 20 Lectures" in the backend of the "Xiaobai Learns Vision" public account to download 20 practical projects based on OpenCV for advanced OpenCV learning.
Group Chat
Welcome to join the reader group of the public account to exchange with peers. Currently, there are WeChat groups for SLAM, 3D vision, sensors, autonomous driving, computational photography, detection, segmentation, recognition, medical imaging, GAN, algorithm competitions, etc. (these will gradually be subdivided). Please scan the WeChat number below to join the group, and note: "Nickname + School/Company + Research Direction", for example: "Zhang San + Shanghai Jiao Tong University + Vision SLAM". Please follow the format; otherwise, it will not be approved. After successfully adding, you will be invited to join relevant WeChat groups based on research direction. Please do not send advertisements in the group; otherwise, you will be removed from the group. Thank you for your understanding~
