Nature Communications
2020 Jan 9
IF: 17.694
Introduction:
GAN includes a generator that outputs realistic silicon-generated samples. This is achieved through a neural network that learns to transform a simple low-dimensional distribution into a high-dimensional distribution, which is indistinguishable from the actual training distribution.
In this paper, the authors establish a single-cell GAN (scGAN) to generate real scRNA-seq data. scGAN can produce specific cell types or subpopulations as needed using conditioning (cscGAN), increasing sparse cell populations to enhance the quality and robustness of downstream classification.
Methods:
Model Description:
scGAN:
First, the authors outline the model used for scGAN by defining the loss function optimized by scGAN, the optimization process, and key elements of the model architecture. GAN typically involves two artificial neural networks: one generator that trains to output real samples given some input random noise, and one discriminator that trains to detect the differences between real cells and cells generated by the generator. The adversarial training process allows these entities to compete with each other in a mutually beneficial way. Formally, GAN minimizes the difference between the distributions of real samples and generated samples. Different divergences yield different GAN variants. While the original GANs minimized the so-called Jensen-Shannon divergence, they have known flaws that make their optimization difficult. For instance, they are known to be prone to mode collapse, where the generated samples are real but only represent a small fraction of the trained sample types. On the other hand, WGAN uses Wasserstein distance, which has compelling theoretical and empirical justification. In experiments, WGAN showed no signs of mode collapse and displayed stable and robust training in hyperparameter optimization. In contrast, earlier attempts to train the original GAN on scRNA-seq data never resulted in convergence, whereas WGAN implementations did achieve convergence. This does not mean that it is impossible to successfully train the original GAN on these data.
Let Pr and Ps denote the distributions of real units and generated units, respectively. The Wasserstein distance between them, also known as the Earth Mover’s Distance, is defined as follows:
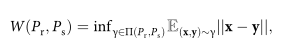
where x and y are random variables, and ∏(Pr, Ps) is the set of all joint distributions γ(x, y) whose marginals are Pr and Ps, respectively. These distributions represent all the ways to move mass from x to y to transform Pr into Ps.
However, in this formula, finding a generator that produces cells from the distribution Ps, thereby minimizing the Wasserstein distance to the real cell distribution, is challenging. However, a more reliable and equivalent formula can be used for the Wasserstein distance, given by the Kantorovich–Rubinstein dual:
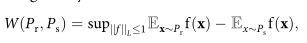
where ||f||L≤1 is the set of 1-Lipschitz functions valued in R. The solution to this problem is approximated by training a neural network, previously referred to as the critic network, whose function is denoted by fc.
The input to the generator is a realization of multivariate noise, whose distribution is represented by Pn. As is common in the literature, a centered Gaussian distribution with unit diagonal covariance (i.e., multivariate white noise) is used. The dimension of the Gaussian distribution defines the size of the latent space of the GAN. The dimension of this latent space should reflect the intrinsic dimension of the scRNA-seq expression data we are learning from, and is expected to be significantly smaller than their apparent dimension (i.e., the total number of genes).
If fg represents the function learned by the generator network, the optimization problem solved by scGAN is the same as that of the Wasserstein GAN:
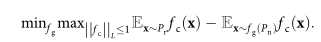
The Lipschitz constraint is implemented using the gradient penalty term proposed by Gulrajani et al.
Therefore, training the scGAN model requires solving the so-called min/max problem. Since an analytical solution to this problem cannot be found, the authors resort to numerical optimization schemes. Essentially following the same approach as most GAN literature, they adopt an alternating scheme between maximizing the discriminator loss (five iterations) and minimizing the generator loss (one iteration). For minimization and maximization, the authors used a recent algorithm called AMSGrad, which addresses some shortcomings of the widely used Adam algorithm, leading to more stable training and convergence to more appropriate saddle points. The AMSGrad exponential decay parameters β1 are set to 0.5 and β2 to 0.9.
Regarding the architecture of the discriminator and generator networks, most existing image literature prescribes the use of convolutional neural networks (CNNs). In natural images, spatially proximate pixels exhibit stronger and more complex interdependencies. Moreover, spatial translation of objects in images typically does not alter their meaning. CNNs are designed to leverage these two properties. However, these properties do not apply to scRNA-seq data, as the order of genes is mostly arbitrary and fixed for all cells. In other words, there is no reason to believe that CNNs are sufficient, which is why scGAN uses fully connected (FC) layers. Using MLPs with FC layers having 256, 512, and 1024 neurons as the generator, and MLPs with 1024, 512, and 256 neurons FC as the critic, optimal results were obtained. In the outermost layer of the discriminator network, no activation function is used. For every other layer of the discriminator and generator networks, the Rectified Linear Unit (ReLU) is used as the activation function.
Naturally, the optimal parameters in each layer of the artificial neural network are highly dependent on the parameters of the previous and subsequent layers. However, these parameters change during the training process of each layer, altering the distribution of inputs to subsequent layers and slowing down the training process. To mitigate this effect and accelerate the training process, normalization layers, such as batch normalization, are typically used for each training mini-batch. It was found that optimal results can be obtained when batch normalization is used at every layer of the generator. Finally, as described in the dataset and preprocessing section, each real sample used for training has been normalized for library size. A custom LSN layer is now introduced, which forces scGAN to explicitly generate cells with a fixed library size.
LSN Layer:
A notable feature of scRNA-seq is the variable range of gene expression levels across all cells. Importantly, even for cells within the same cell subpopulation, scRNA-seq data is highly heterogeneous. In the field of machine learning, training on this data becomes easier through the use of input normalization. Normalizing inputs yields features with similar ranges that produce stable gradients. The scRNA-seq normalization method used includes LSN, where the total read count for each cell is exactly 20000.
It can be found that training scGAN on library size normalized scRNA-seq data helps improve training and enhance the quality of generated cells based on evaluation criteria (model selection methods). Providing library size normalized cells for the training of scGAN means that the generated cells should possess the same properties. Ideally, the model will inherently learn this property. In practice, to accelerate the training process and make it smoother, the aforementioned LSN layer was added at the output end of the generator. The LSN layer readjusts its input (x) to ensure each unit has a fixed total read count (φ):
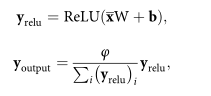
where W and b are its weights and biases, and (yrelu)i denotes the i-th component of the yrelu vector.
cscGAN:
The authors’ cscGAN model utilizes conditional information about each cell type or subpopulation to further generate specific types of cells. Integrating this auxiliary information during the generation process is known as conditional action. In recent years, several extensions have been proposed for GANs to allow for such conditioning. It is worth noting that these extensions are available regardless of the type of GAN at hand.
The authors explored two conditional modulation techniques, Auxiliary Classifier (ACGAN) and Projection-based Conditional Modulation (PCGAN). The former adds a classification loss term to the objective. The latter implements class labels as an inner product at the output end of the discriminator. While results obtained with ACGAN are also reported, the best outcomes were achieved through projection modulation.
In practice, PCGAN differs from the previously described scGAN in that (i) it has multiple critical output layers, one for each cell type, and (ii) it uses conditional BNL27, whereby the learned singular scaling and shifting factors of BNL are replaced by one for each cell type.
Discussion:
This work demonstrates how cscGAN can be used to generate realistic scRNA-seq data representations with various cell types and millions of cells. cscGAN outperforms current methods in the actual generation of scRNA-seq data and exhibits sublinear scaling with respect to cell numbers. Most importantly, the evidence provided suggests that generating scRNA-seq data in silico can improve downstream applications, especially when sparse and under-represented cell populations are augmented by cells generated by cscGAN.
While this paper focuses on the task of cell type classification, many other applications are likely to benefit from data augmentation, including but not limited to clustering itself, cell type detection, and data denoising. It is noteworthy that any other type of auxiliary information (sample segmentation) can be used similarly. For example, cscGAN can be conditioned and trained based on combinations of case and control samples. In summary, data augmentation may be particularly useful when dealing with human data, as human data is notoriously heterogeneous due to genetic and environmental variations. Data generation and augmentation may be most valuable when dealing with rare diseases or when specific ethnic or gender samples are lacking.
Reference: Realistic in silico generation and augmentation of single-cell RNA-seq data using generative adversarial networks
PMID: 31919373
DOI: 10.1038/s41467-019-14018-z
