Engineer friends often ask me: “Graph deep learning” sounds impressive, but are there any major success stories in business? Has it been deployed in actual apps?

Besides the recommendation systems of Pinterest, Alibaba, and Twitter, a notable success is the Transformer architecture, which has brought a storm in NLP.

Through this article, I aim to establish a connection between Graph Neural Networks (GNNs) and transformers. I will discuss the intuition behind model architectures in the NLP and GNN communities, using equations and graphs to connect the two, and discuss how to bring both together to make progress.

Let’s first talk about the purpose of model architecture – representation learning.

Representation Learning in NLP

At a high level, all neural network architectures construct input data into vector/embedding “representations” that encode useful statistical and semantic information related to the data. These latent or hidden representations can be used to perform useful tasks, such as classifying images or translating sentences. Neural networks “learn” by receiving feedback (typically through error/loss functions), building increasingly better representations.

For Natural Language Processing (NLP), typically, Recurrent Neural Networks (RNNs) construct representations of each word in a sentence sequentially, i.e., one word at a time. Intuitively, we can think of RNN layers as a conveyor belt, processing the text recursively from left to right. In the end, we obtain hidden features for each word in the sentence, which we pass to the next RNN layer or use for our NLP tasks.

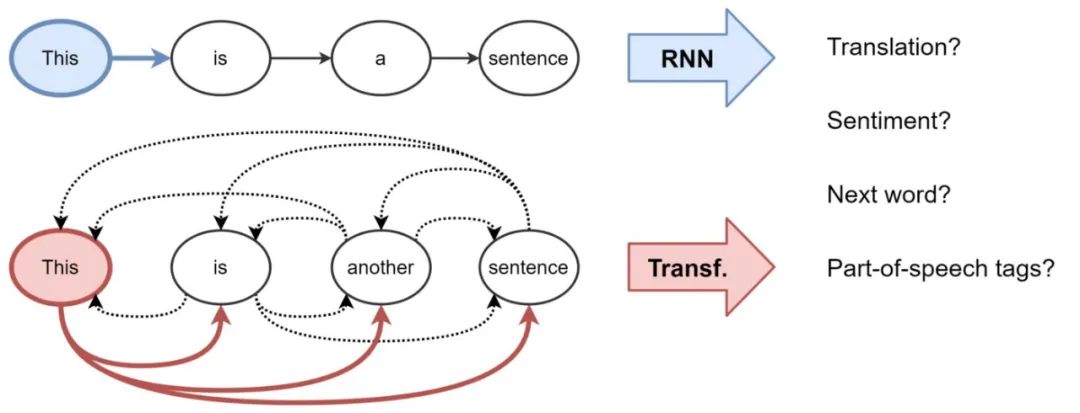
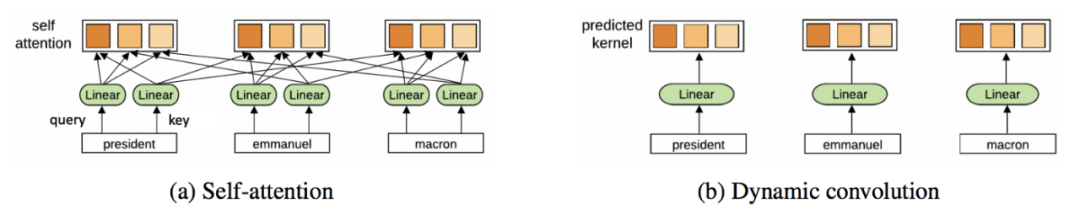
Transformers were initially introduced for machine translation and have gradually replaced RNNs in mainstream NLP. This architecture uses a completely new way to perform representation learning: without recursion, Transformers use attention mechanisms to build features for each word, determining the importance of other words in the sentence to the preceding words. Knowing this, the feature update for a word is the weighted sum of linear transformations of all other word features, based on their importance.

Breaking Down the Transformer

Let’s develop intuition about the architecture by translating the previous paragraph into mathematical symbols and vector language. We update the hidden feature h of the i-th word from layer l to layer l+1 in the sentence S:

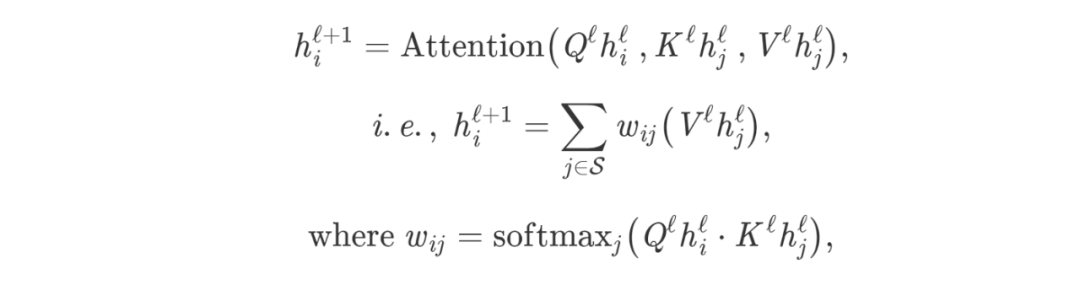
Where j∈S represents the set of words in the sentence, and Q, K, V are learnable linear weights (representing the Query, Key, and Value for attention computation, respectively). For Transformers, the attention mechanism is executed in parallel for each word in the sentence, while RNNs update one word at a time.

Through the following pipeline, we can better understand the attention mechanism:

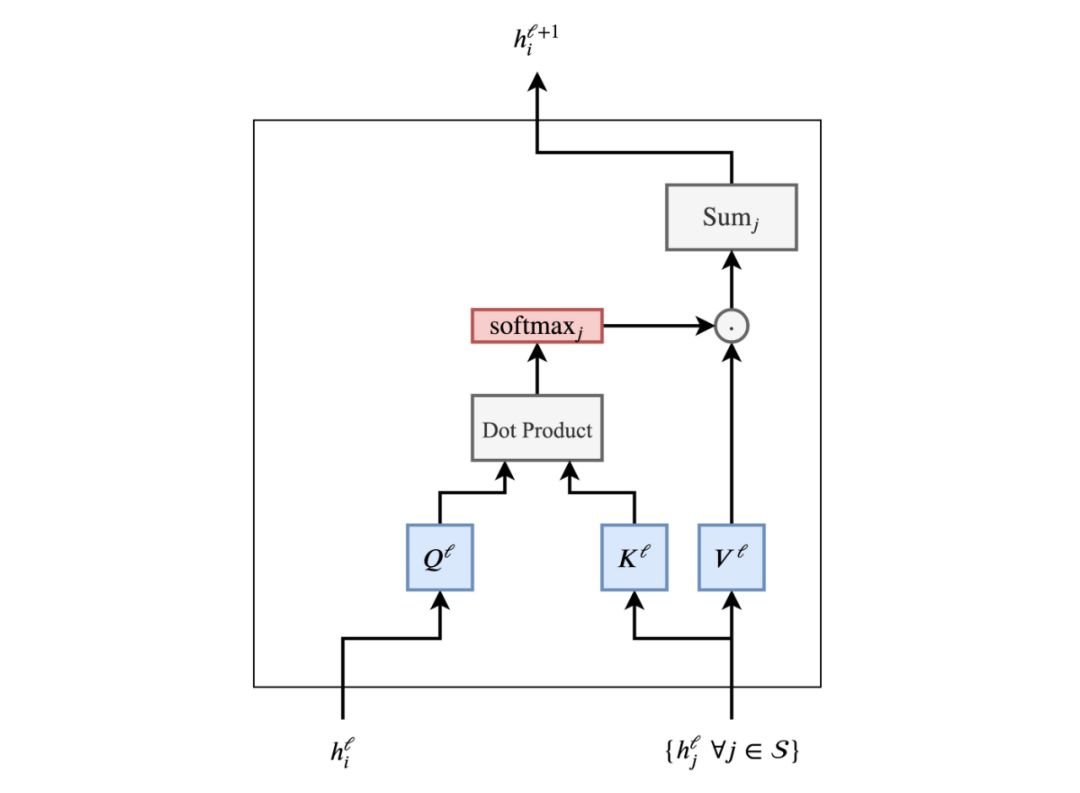
Using this word’s feature h_i ^ℓ^ and the features of other words in the sentence h_j ^ℓ^, ∀j∈S, we calculate the attention weight w~ij~ for each pair (i, j) using dot products, then apply softmax to all j. Finally, we perform a weighted sum of all h_j ^ℓ^ to produce the updated word feature h_i ^{ℓ+ 1}. Each word in the sentence undergoes the same pipeline in parallel to update its features.

Multi-Head Attention Mechanism

Making this dot-product attention mechanism work is tricky because random initialization can disrupt the stability of the learning process. We can overcome this issue by executing multiple “heads” of attention in parallel and concatenating the results (now each head has independent learnable weights):

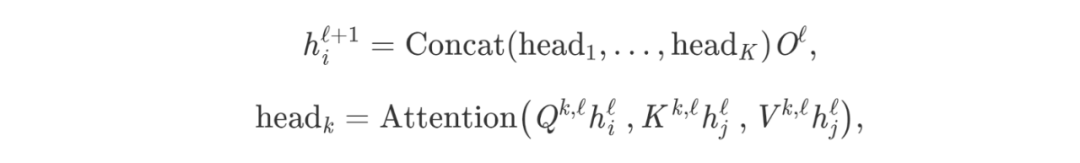
Where Q^k^, K^k^, V^k^ are the learnable weights of the k-th attention head, and O is a dimensionality reduction projection to match feature dimensions.

Multiple heads allow the attention mechanism to effectively “hedge bets,” observing different transformations or aspects of the hidden features from the previous layer. We will discuss this in detail later.

Scaling Issues and Feedforward Layers

A key issue in the Transformer architecture is that the features of words after the attention mechanism may be of different scales, (1) this is due to the potentially very shaped distribution of weights when summing the features of other words. (2) At the level of individual feature vectors, concatenating multiple attention heads may output values of different scales, leading to a final value with a wide dynamic range. Based on traditional ML experience, it seems reasonable to add a normalization layer in the pipeline.

The Transformer overcomes this issue through LayerNorm, which normalizes at the feature level and learns affine transformations. Additionally, scaling the dot-product attention by the square root of the feature dimension helps mitigate issue (1).

Finally, the authors propose another “trick” to control the scaling issue: a position-wise 2-layer MLP. After multi-head attention, they project the vector *h_i ^{ℓ + 1}* to a higher dimension through a learnable weight, then project back to the original size through ReLU, followed by another normalization:

Honestly, I’m not sure what the exact intuition is behind this overly parameterized feedforward sublayer, and it seems no one has questioned it! I think LayerNorm and scaled dot products don’t completely solve this issue, so the large MLP is a hack to independently rescale the feature vectors.

The final appearance of the Transformer layer looks like this:

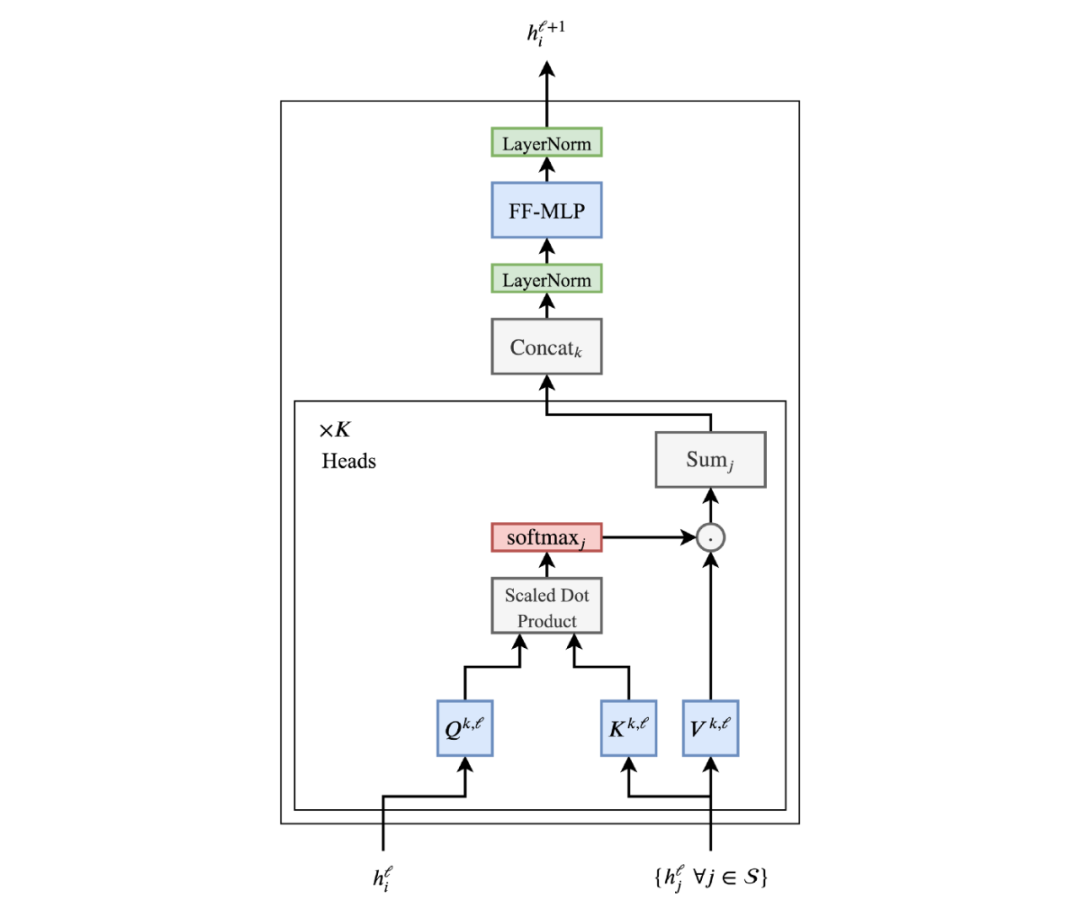
The Transformer architecture is also very suitable for deep networks, enabling the NLP community to scale in both model parameters and data. The residual connections between each multi-head attention sublayer and feedforward sublayer are key to stacking Transformer layers (but omitted in the diagram for clarity).

Building Graph Representations with GNNs

Let’s temporarily step away from NLP.

Graph Neural Networks (GNNs) or Graph Convolutional Networks (GCNs) build representations of nodes and edges in graph data. They achieve this through neighborhood aggregation (or message passing), where each node collects features from its neighborhood to update the representation of its surrounding local graph structure. Stacking several GNN layers allows the model to propagate features of each node throughout the entire graph – spreading from its neighbors to the neighbors’ neighbors, and so on.

In its most basic form, a GNN at layer ℓ aggregates features of the node itself and its neighboring nodes through a nonlinear transformation to update the hidden feature h of node i:

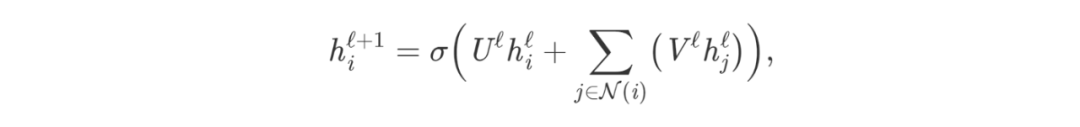
Where U, V are the learnable weight matrices for the GNN layer, and σ is a nonlinear transformation such as ReLU.

The sum of neighboring nodes *j∈N(i)* can be replaced by other input-size invariant aggregation functions, such as simple mean/max, or more powerful functions like the weighted sum through attention mechanisms.

Sound familiar?

Perhaps a pipeline helps establish the connection:

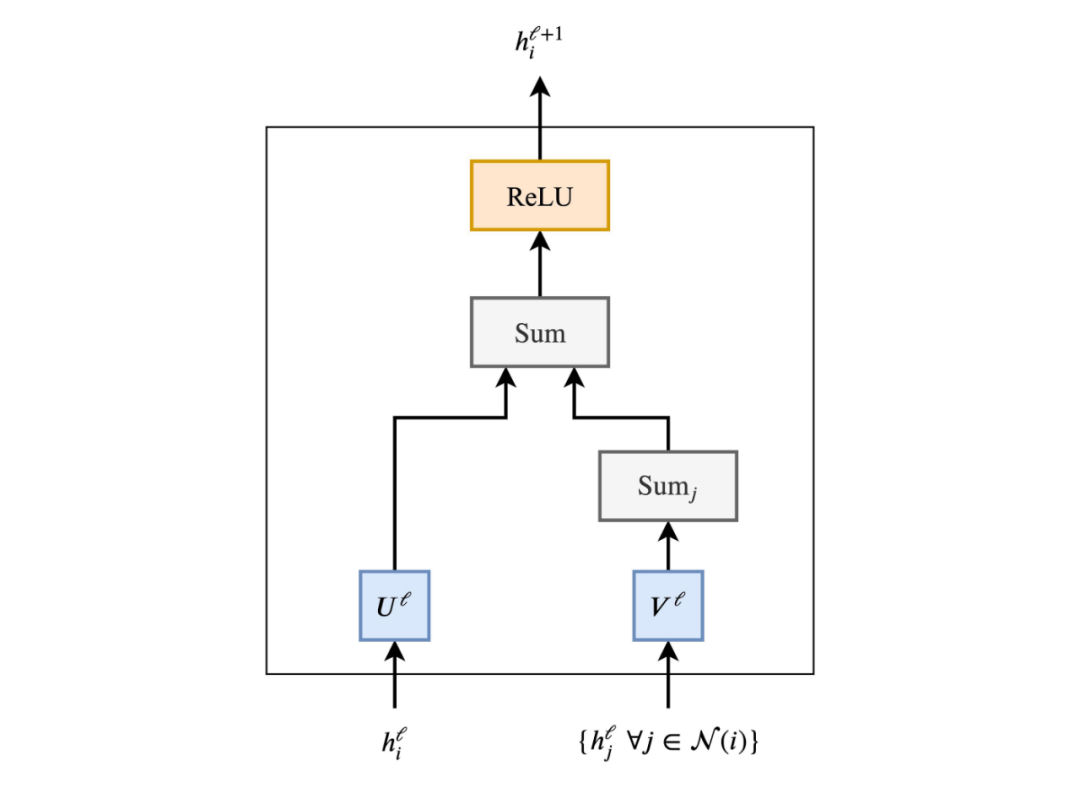
If we aggregate multiple parallel neighborhood heads and replace the summation of neighborhood j with an attention mechanism, i.e., a weighted sum, we obtain Graph Attention Networks (GAT). Adding normalization and feedforward MLP, we see we have a Graph Transformer!

A Sentence is a Fully Connected Word Graph

To make this connection clearer, we can view a sentence as a fully connected graph where each word is connected to every other word. Now, we can use GNNs to build features for each node (word) in the graph (sentence), and then we can use it to execute NLP tasks.

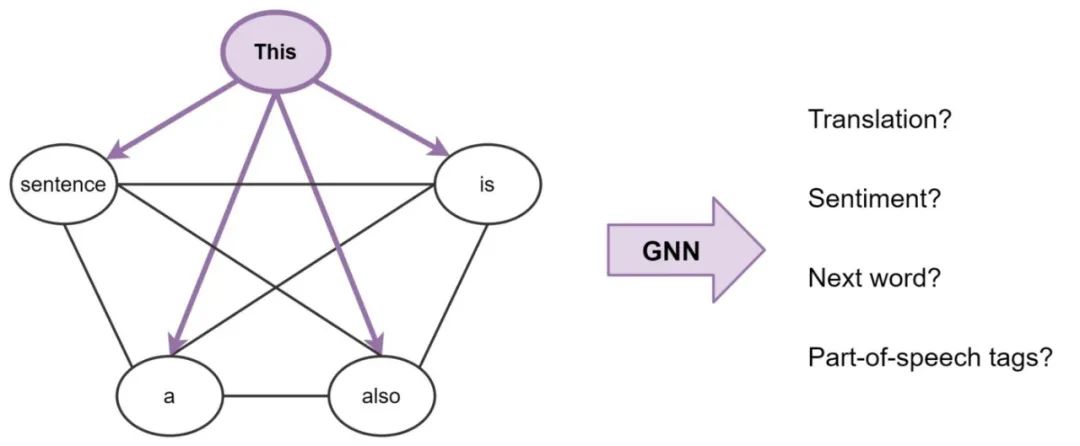
In general, this is what Transformers are doing: they are GNNs with multi-head attention as the aggregation function for neighbors. Standard GNNs aggregate features from their local neighboring nodes j∈N(i), while NLP Transformers treat the entire sentence S as local neighbors, aggregating features from every word j∈S at each layer.

Importantly, various tricks for specific problems — such as positional encoding, causal/hiding aggregation, learning rate strategies, and pre-training — are crucial for the success of Transformers but rarely appear in the GNN community. At the same time, viewing Transformers from the GNN perspective can help us shed many fancy aspects of the architecture.

What Can We Learn From Each Other?

Now that we have established a connection between Transformers and GNNs, let me discuss…

Is Fully Connected Graph the Best Input Format for NLP?

Before statistical NLP and ML, linguists like Noam Chomsky focused on developing formal theories of language structure, such as syntax trees/graphs. Tree LSTMs have tried this, but perhaps transformers/GNNs are better architectures that can bring the world of linguistic theory closer to statistical NLP?

How to Learn Long-Term Dependencies?

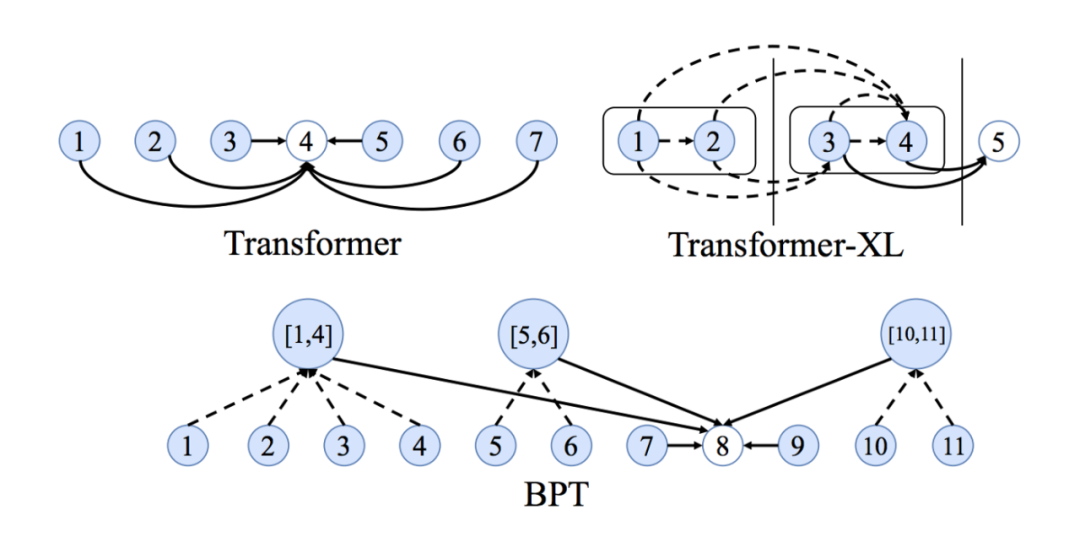
Another issue with fully connected graphs is that they make learning long-term dependencies between words difficult. This is simply due to how the number of edges in a graph grows quadratically with the number of nodes. In a sentence with n words, a Transformer/GNN will compute for n^2^ word pairs. For very large n, this becomes unmanageable.

The NLP community has interesting views on the long sequence and dependency problem: making the attention mechanism sparse or adaptive to input size, adding recursion or compression at each layer, using locality-sensitive hashing for efficient attention, are all promising new ideas to improve Transformers.

It would be interesting to see ideas from the GNN community join in, such as using bipartite graph partitioning for sentence graph sparsification seems like another exciting approach.

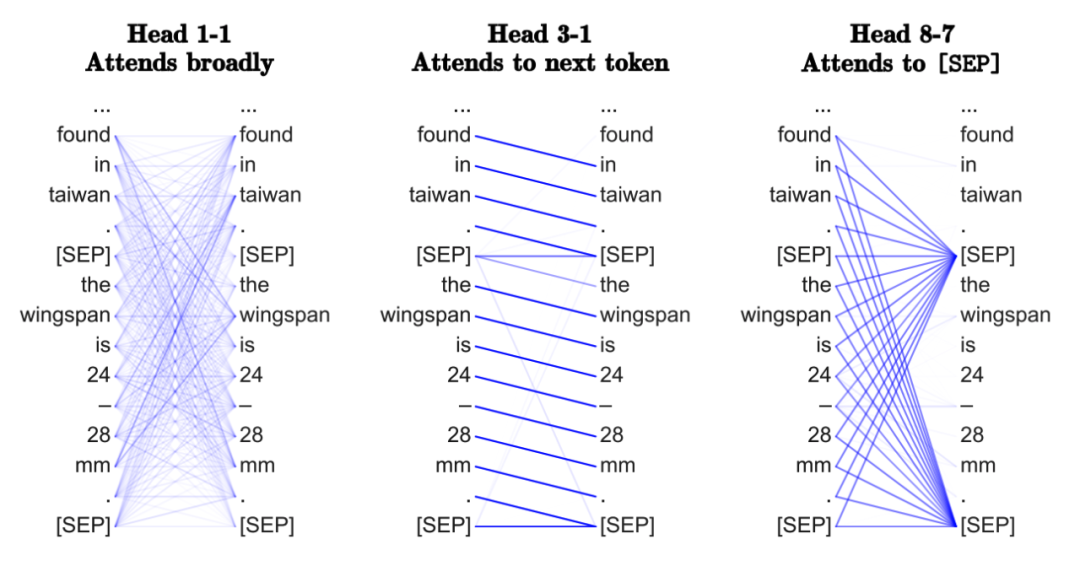
Are Transformers Learning “Neural Syntax”?

There are several intriguing papers from the NLP community regarding what Transformers might be learning. The basic premise is that by attending to all words in a sentence, to determine which words to focus on, “Transformers” may be able to learn something akin to specific task syntax. In multi-head attention, different heads may also “look” at different syntactic properties.

In graph terms, can we recover the most important edges (and what they might contain) from how GNN performs neighbor aggregation at each layer across the entire graph? I’m not so convinced of this perspective.

Why Multi-Head Attention? Why Attention?

I tend to agree with the optimization view of the multi-head mechanism — having multiple attention heads improves learning and overcomes bad random initialization. For example, these papers suggest that Transformer heads can be “pruned” or removed during training without significantly affecting performance.

The multi-head neighbor aggregation mechanism has also proven effective in GNNs; for instance, GAT uses the same multi-head attention and MoNet uses multiple Gaussian kernels to aggregate features. Although invented to stabilize the attention mechanism, could the multi-head mechanism become a standard operation for squeezing model performance?

Conversely, GNNs with simple aggregation functions (like sum or max) do not require multiple aggregation heads for stable training. Wouldn’t it be better for Transformers if we didn’t have to compute compatibility between each pair of words in a sentence?

Can Transformers benefit from completely shedding attention? Recent work by Yann Dauphin and collaborators proposed an alternative ConvNet architecture. Transformers may eventually do something similar.

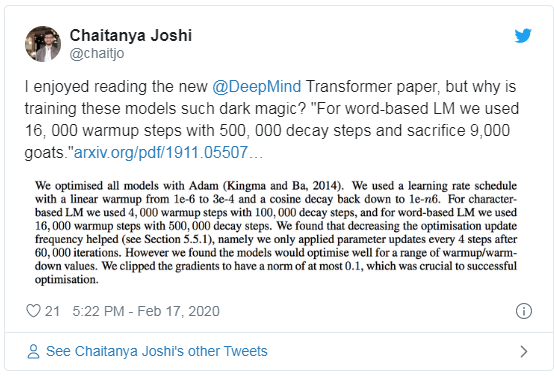
Why is Training Transformers So Difficult?

Reading new papers on Transformers makes me feel that training these models requires something akin to “black magic” when determining the best learning rate strategies, warmup strategies, and decay settings. This may simply be due to the models being too large and the NLP research tasks being too challenging.

Recent findings suggest it may also be due to the specific arrangements of normalization and residual connections within the architecture.

At this point, I’m frustrated, but it makes me wonder: do we really need the expensive pairwise attention of multiple heads, overly parameterized MLP layers, and complex learning rate strategies?

Do we really need to have models this large?

For the task at hand, shouldn’t architectures with good inductive bias be easier to train?

Further Reading

This blog is not the first to connect GNNs and Transformers: here’s a fantastic talk by Arthur Szlam on the history and connections between attention/memory networks, GNNs, and Transformers: https://ipam.wistia.com/medias/1zgl4lq6nh. Similarly, DeepMind’s star-studded position paper introduced a framework for graph networks, unifying all these ideas. The DGL team has a great tutorial on transforming seq2seq problems into GNNs: https://docs.dgl.ai/en/latest/tutorials/models/4_old_wines/7_transformer.html