Introduction
Recently, Renmin University of China, in collaboration with Tencent AI Lab, Tsinghua University, Stanford, and other institutions, published a review paper: “A Survey of Geometric Graph Neural Networks: Data Structures, Models and Applications.” This review systematically organizes the relevant literature on geometric graph neural networks based on a brief introduction to theoretical knowledge such as group theory and symmetry, covering data structures, models, and numerous scientific applications.Keywords: Geometric Graph Neural Networks, AI for Science, Graph Base Models, Large Language Models
XS | EditorScienceAI | Source In November 2023, Nature published two significant results: the protein generation method Chroma and the crystal material design method GNoME, both using graph neural networks as tools for representing scientific data. In fact, graph neural networks, especially geometric graph neural networks, have been essential tools in scientific intelligence (AI for Science) research. This is because physical systems such as particles, molecules, proteins, and crystals in the scientific field can all be modeled as a special data structure—geometric graphs. Unlike general topological graphs, geometric graphs incorporate essential spatial information to better describe physical systems, needing to satisfy physical symmetries of translation, rotation, and reflection. Given the advantages of geometric graph neural networks in modeling physical systems, various methods have emerged in recent years, with the number of papers continuing to grow. Recently, Renmin University of China, in collaboration with Tencent AI Lab, Tsinghua University, Stanford, and other institutions, published a review paper: “A Survey of Geometric Graph Neural Networks: Data Structures, Models and Applications.” This review systematically organizes the relevant literature on geometric graph neural networks based on a brief introduction to theoretical knowledge such as group theory and symmetry, covering data structures, models, and numerous scientific applications.
Paper link: https://arxiv.org/abs/2403.00485GitHub link: https://github.com/RUC-GLAD/GGNN4Science
In this review, the authors surveyed over 300 references, summarizing three different geometric graph neural network models, introducing relevant methods for 23 different tasks in various scientific data such as particles, molecules, and proteins, and collecting over 50 relevant benchmark datasets. Finally, the review looks forward to future research directions, including geometric graph base models and integration with large language models. Below is a brief introduction to each chapter.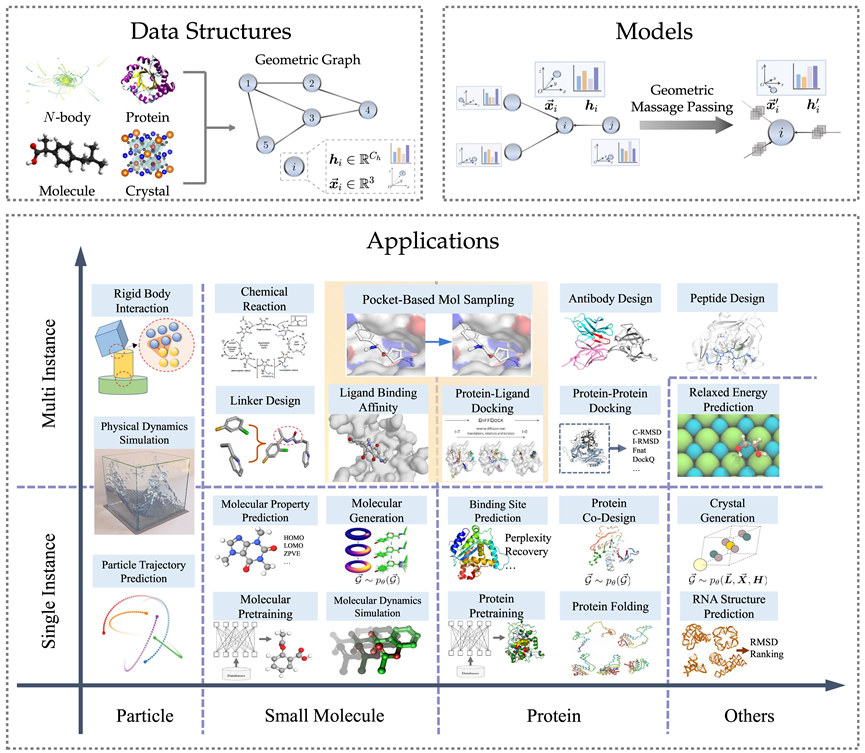
Geometric Graph Data Structures
Geometric graphs consist of adjacency matrices, node features, and node geometric information (e.g., coordinates). In Euclidean space, geometric graphs typically exhibit physical symmetries of translation, rotation, and reflection, generally characterized by groups that describe these transformations, including Euclidean groups, translation groups, orthogonal groups, permutation groups, etc. Intuitively, it can be understood as a combination of four operations: permutation, translation, rotation, and reflection in a certain order. For many AI for Science fields, geometric graphs are a powerful and universal representation method that can represent numerous physical systems, including small molecules, proteins, crystals, and physical point clouds.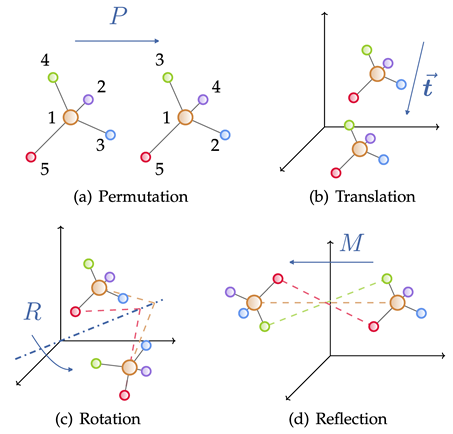
Geometric Graph Neural Network Models
Based on the requirements for symmetry in solving objectives in practical problems, this article categorizes geometric graph neural networks into three types: invariant (invariant) models, equivariant (equivariant) models, and the Geometric Graph Transformer inspired by the Transformer architecture, where equivariant models are further divided into Scalarization-Based Models and High-Degree Steerable Models based on spherical harmonics. Following the above rules, the article collected and categorized well-known geometric graph neural network models in recent years.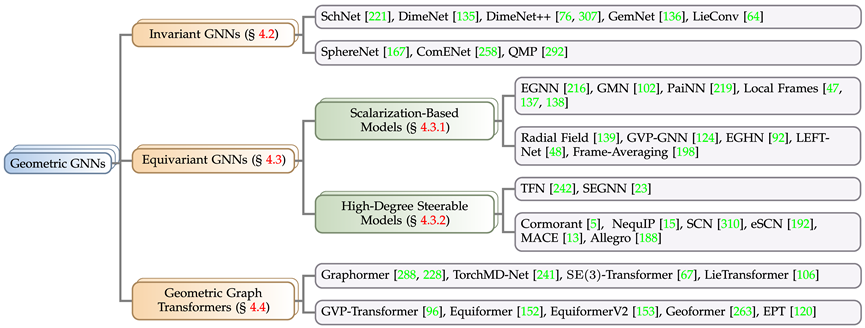
Here we briefly introduce the representative works of the invariant model (SchNet[1]), Scalarization-Based Model (EGNN[2]), and High-Degree Steerable Model (TFN[3]), highlighting their connections and distinctions. It can be observed that all three adopt a message-passing mechanism, but the latter two, as equivariant models, additionally introduce a single geometric message passing. The invariant model primarily utilizes the features of the nodes themselves (e.g., atomic type, mass, charge, etc.) and the invariant features between atoms (e.g., distance, angle[4], dihedral angle[5]) for message computation, followed by propagation. On top of that, the Scalarization-Based Model additionally introduces geometric information through the coordinate differences between nodes and uses invariant information as weights for the geometric information in a linear combination, achieving the introduction of equivariance. The High-Degree Steerable Model uses higher-order spherical harmonics (Spherical Harmonics) and Wigner-D matrices to represent the geometric information of the system; this method manipulates the degree of irreducible representations using Clebsch–Gordan coefficients from quantum mechanics, thus facilitating the geometric message passing process.
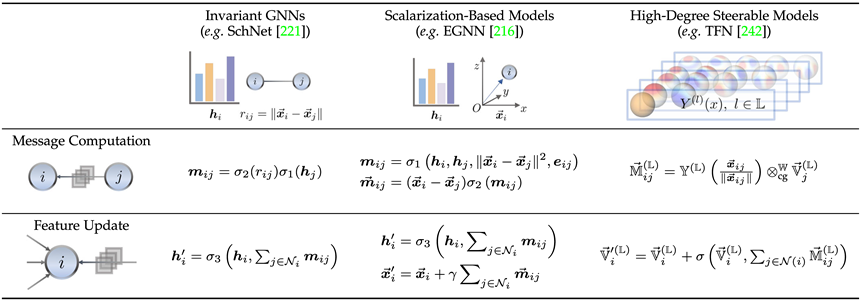The geometric graph neural networks designed in this way ensure significant improvements in accuracy due to their guaranteed symmetry, and they also shine in generative tasks. The following figure shows the results of geometric graph neural networks compared to traditional models in molecular property prediction, protein-ligand docking, and antibody design (generation) tasks across the QM9, PDBBind, and SabDab datasets, clearly demonstrating the advantages of geometric graph neural networks.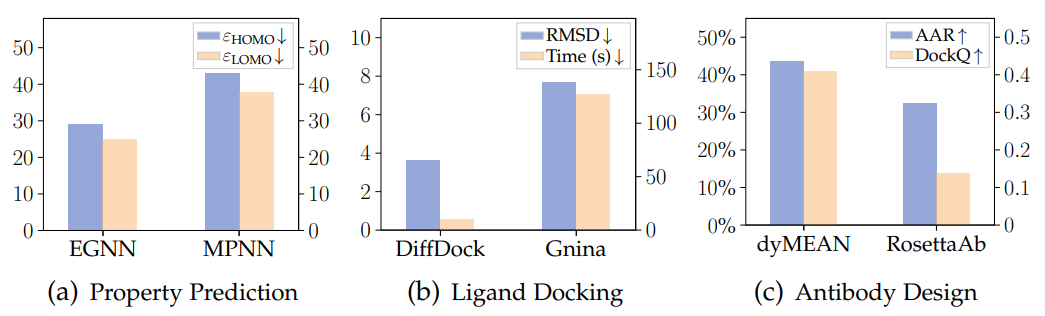
Scientific Applications
In terms of scientific applications, the review covers various application scenarios including physics (particles), biochemistry (small molecules, proteins), and others such as crystals, defining tasks and the required types of symmetry, introducing commonly used datasets and classic model design ideas for each task.
The table above displays common tasks and classic models in various fields, where the article separately distinguishes between single-instance and multi-instance tasks (e.g., chemical reactions require multiple molecules to participate), highlighting small molecule-small molecule, small molecule-protein, and protein-protein domains. To better facilitate model design and experimental development in the field, the article statistically summarizes common datasets and benchmarks for both single-instance and multi-instance tasks, recording the sample sizes and task types of different datasets. The following table organizes common single-instance task datasets.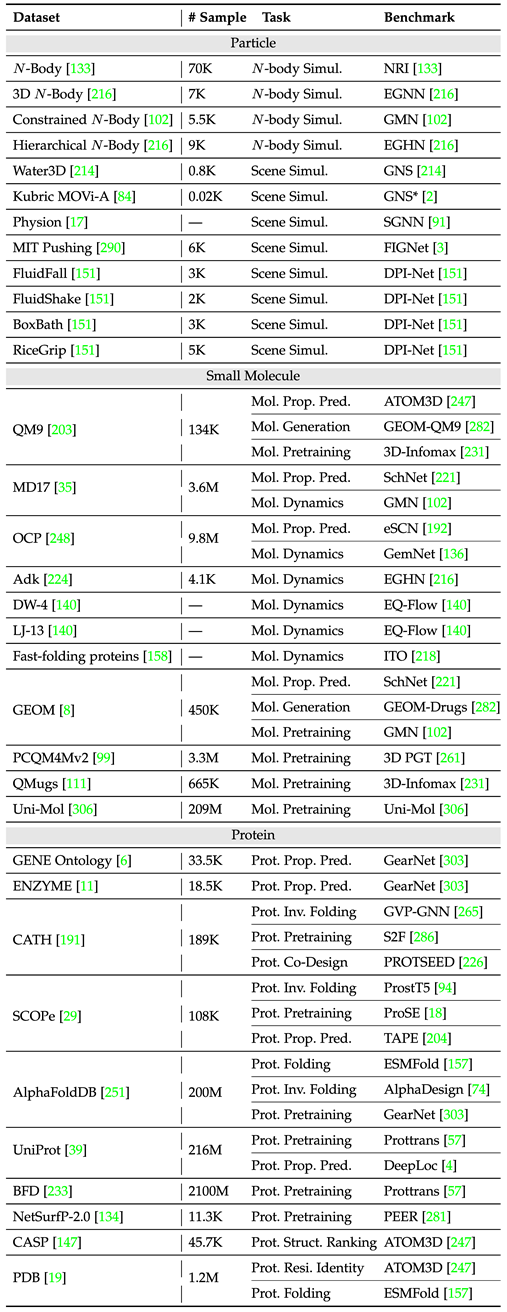
The following table organizes common multi-instance task datasets.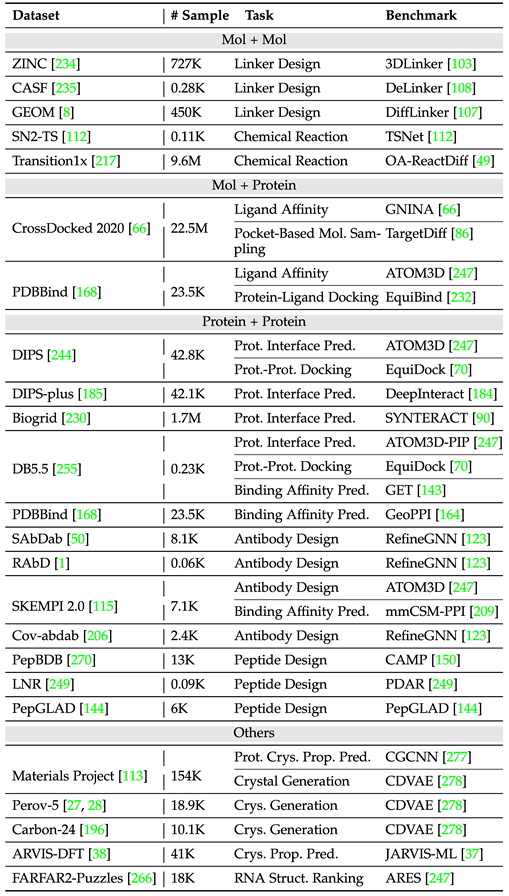
Future Outlook
The article offers preliminary insights on several aspects, hoping to inspire further exploration:1. Geometric Graph Base Models The superiority of adopting a unified base model across various tasks and fields has been vividly demonstrated in the significant advancements of GPT series models. How to reasonably design in the task space, data space, and model space to introduce this idea into the design of geometric graph neural networks remains an interesting open question.2. Efficient Cycle of Model Training and Real-World Experimental Validation The acquisition of scientific data is costly and time-consuming, and models evaluated solely on independent datasets cannot directly reflect feedback from the real world. The importance of achieving an efficient model-reality iterative experimental paradigm, similar to GNoME (which integrates an end-to-end pipeline, including graph network training, density functional theory calculations, and automated laboratories for material discovery and synthesis), will continue to grow.3. Integration with Large Language Models (LLMs) Large language models (LLMs) have been widely proven to possess rich knowledge covering various fields. Although some work has utilized LLMs for certain tasks, such as molecular property prediction and drug design, they only operate on primitives or molecular graphs. How to organically combine them with geometric graph neural networks to enable handling 3D structural information and performing predictions or generation on 3D structures remains a considerable challenge.4. Relaxation of Equivariance Constraints Undoubtedly, equivariance is crucial for enhancing data efficiency and model generalization capabilities, but it is worth noting that overly strong equivariance constraints can sometimes overly restrict the model, potentially harming its performance. Therefore, how to balance the designed model between equivariance and adaptability is a very interesting problem. Exploration in this area can not only enrich our understanding of model behavior but also pave the way for developing more robust and versatile solutions, making them applicable in broader contexts.
References
[1] Schütt K, Kindermans P J, Sauceda Felix H E, et al. Schnet: A continuous-filter convolutional neural network for modeling quantum interactions[J]. Advances in neural information processing systems, 2017, 30.[2] Satorras V G, Hoogeboom E, Welling M. E (n) equivariant graph neural networks[C]//International conference on machine learning. PMLR, 2021: 9323-9332.[3] Thomas N, Smidt T, Kearnes S, et al. Tensor field networks: Rotation-and translation-equivariant neural networks for 3D point clouds[J]. arXiv preprint arXiv:1802.08219, 2018.[4] Gasteiger J, Groß J, Günnemann S. Directional Message Passing for Molecular Graphs[C]//International Conference on Learning Representations. 2019.[5] Gasteiger J, Becker F, Günnemann S. Gemnet: Universal directional graph neural networks for molecules[J]. Advances in Neural Information Processing Systems, 2021, 34: 6790-6802.[6] Merchant A, Batzner S, Schoenholz S S, et al. Scaling deep learning for materials discovery[J]. Nature, 2023, 624(7990): 80-85.
Graph Neural Networks and Combinatorial Optimization Reading Club
The solution to a large number of real-world problems relies on the design and solving of algorithms. Traditional algorithms are designed by human experts, while with the continuous development of artificial intelligence technology, there are increasing cases of algorithms learning algorithms, such as artificial intelligence algorithms represented by neural networks, which is the reason for algorithmic neuralization solving. In the direction of algorithmic neuralization solving, graph neural networks are a powerful tool that can fully utilize the characteristics of graph structures to achieve efficient approximate solutions for high-complexity algorithms. Optimization and control of complex systems based on graph neural networks will be a new future direction after the wave of large models. To explore the development and real-world applications of graph neural networks in algorithmic neuralization solving, the Intelligence Club has jointly initiated the “Graph Neural Networks and Combinatorial Optimization” reading club with Associate Professor Fan Changjun from the College of Systems Engineering at National University of Defense Technology and Associate Professor Huang Wenbing from Renmin University of China. The reading club will focus on related fields of graph neural networks and algorithmic neuralization solving, including neural algorithm inference, combinatorial optimization problem solving, geometric graph neural networks, and the application of algorithmic neuralization solving in AI for Science. The reading club has concluded, and registration now allows joining the community and unlocking replay video access.
For more details, please see: Accelerating the Efficiency of Classic Algorithms, Breaking Through Real-World Technical Bottlenecks: Launch of the Graph Neural Networks and Combinatorial Optimization Reading Club
Recommended Reading
1. Frontier Discussion: How Graph Neural Networks, Combinatorial Optimization, and Large Models Promote Each Other in AI4Science?2.Geometric Deep Learning: Bringing AI to the Physical World | Huang Wenbing’s Sharing and Compilation3. AI Frontiers: Machine Learning Solutions for Combinatorial Optimization Problems | Fan Changjun’s Sharing and Compilation4. Zhang Jiang: The Foundation of Third-Generation Artificial Intelligence Technology—From Differentiable Programming to Causal Reasoning | New Course from Intelligence Academy5. With the Year of the Dragon Rising, It’s Time to Learn! Unlock All Content from Intelligence Academy and Start Your New Year Learning Plan6. Join Intelligence, Let’s Get Complex!
Click “Read the Original” to register for the reading club