Source: Machine Learning Algorithms
This article is about 2400 words long and is suggested to be read in 5 minutes.
This article illustrates the Self-Attention mechanism.
1. Difference Between Attention Mechanism and Self-Attention Mechanism
The difference between Attention mechanism and Self-Attention mechanism:
The traditional Attention mechanism occurs between the elements of the Target and all elements in the Source.
In simple terms, the calculation of weights in the Attention mechanism requires the Target to participate. In an Encoder-Decoder model, the calculation of Attention weights requires not only the hidden states in the Encoder but also the hidden states in the Decoder.
Self-Attention:
It is not the Attention mechanism between the input sentence and the output sentence, but the Attention mechanism occurring between the elements within the input sentence or the output sentence.
For example, in a Transformer, when calculating the weight parameters, converting the word vectors into corresponding KQV only requires matrix operations at the Source and does not need information from the Target.
2. Purpose of Introducing Self-Attention Mechanism
The input received by the neural network consists of many vectors of different sizes, and there are certain relationships between different vectors. However, during actual training, it is impossible to fully leverage these relationships, resulting in poor model training outcomes. For example, in machine translation problems (sequence-to-sequence problems where the machine decides how many labels to use), part-of-speech tagging problems (one vector corresponds to one label), semantic analysis problems (multiple vectors correspond to one label), and other text processing issues.
To address the issue that fully connected neural networks cannot establish correlations for multiple related inputs, the Self-Attention mechanism is introduced. The Self-Attention mechanism aims to make the machine pay attention to the relationships between different parts of the entire input.
3. Detailed Explanation of Self-Attention
For an input of a set of vectors, the output is also a set of vectors, where the input length is N (N can vary), and the output is also a vector of length N.
3.1 Single Output
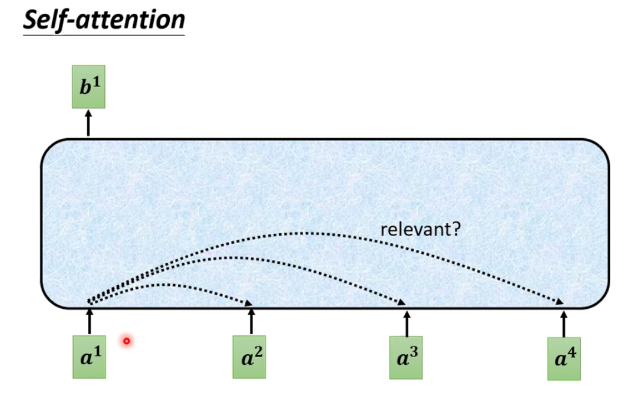
For each input vector a, after going through the blue part of self-attention, it outputs a vector b. This vector b considers the influence of all the input vectors on a1. If there are four word vectors a, there will be four output vectors b.
Taking b1’s output as an example:
First, how to calculate the correlation degree between each vector in the sequence and a1, there are two methods.
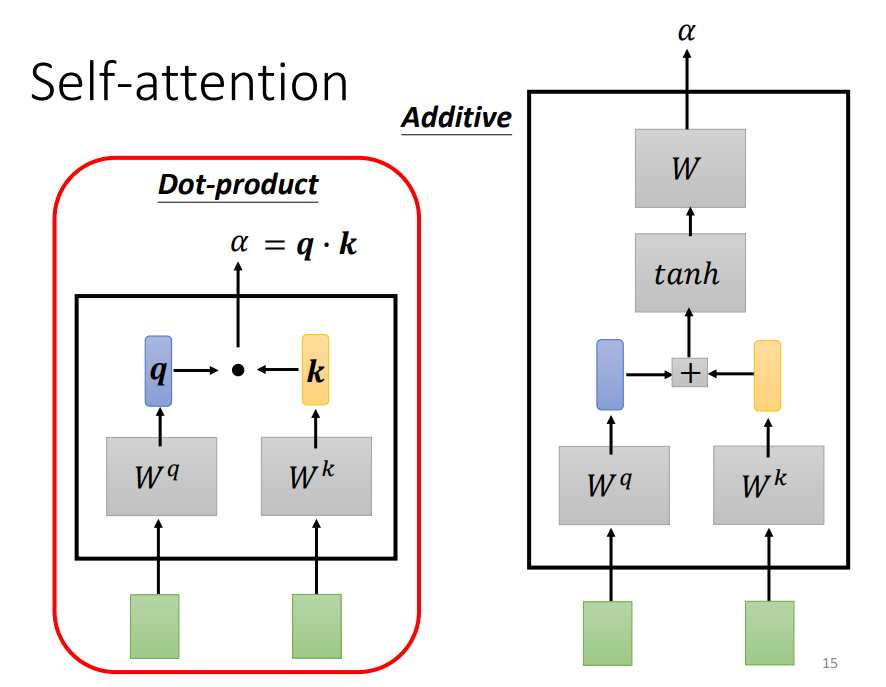
The Dot-product method involves multiplying two vectors by different matrices w to obtain q and k, then performing a dot product to get α. The transformer uses the Dot-product.
The green part in the above image represents the input vectors a1 and a2, while the gray Wq and Wk are weight matrices that need to be learned and updated. Using a1 multiplied by Wq gives a vector q, and using a2 multiplied by Wk gives a value k. Finally, the dot product of q and k yields α, which represents the correlation degree between the two vectors.
The additive model on the right side of the image also involves multiplying the input vector by the weight matrix and then adding, projecting to a new function space using tanh, and multiplying by the weight matrix to obtain the final result.
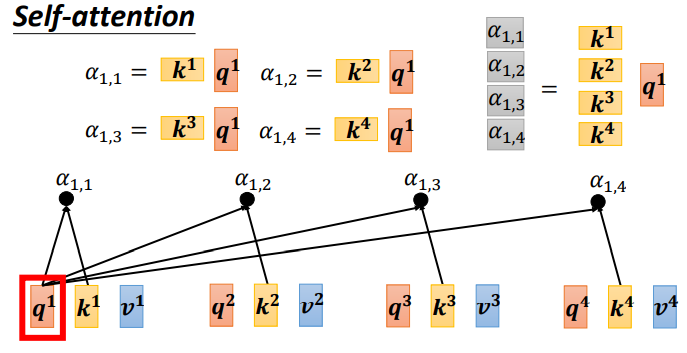
Each α (also known as the attention score) can be calculated, where q is called query and k is called key.
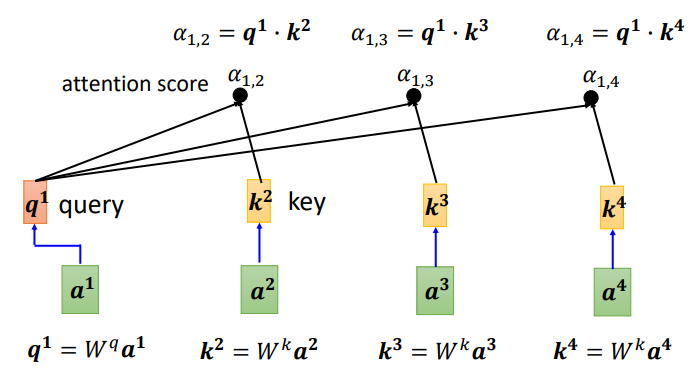
Additionally, the correlation of a1 with itself can also be calculated. After obtaining the correlation degree of each vector with a1, a softmax function is used to calculate an attention distribution, which normalizes the correlation degree. The values indicate which vectors are most related to a1.
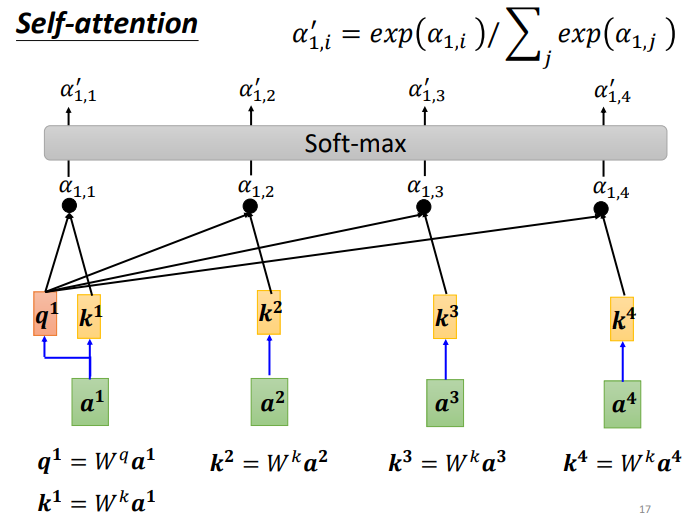
Next, important information from the sequence needs to be extracted based on α′:
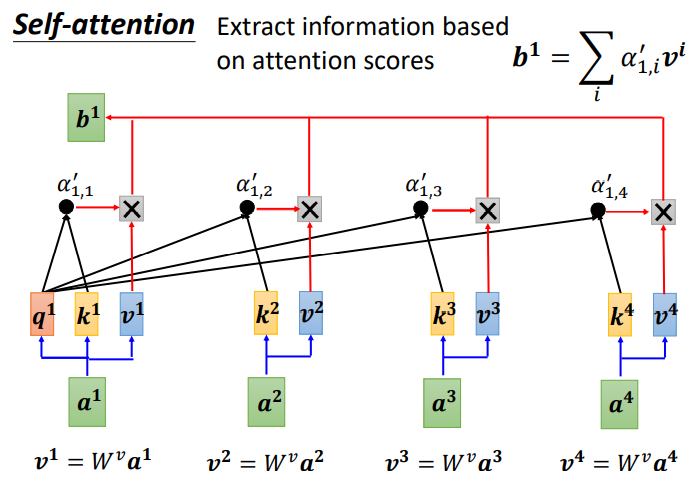
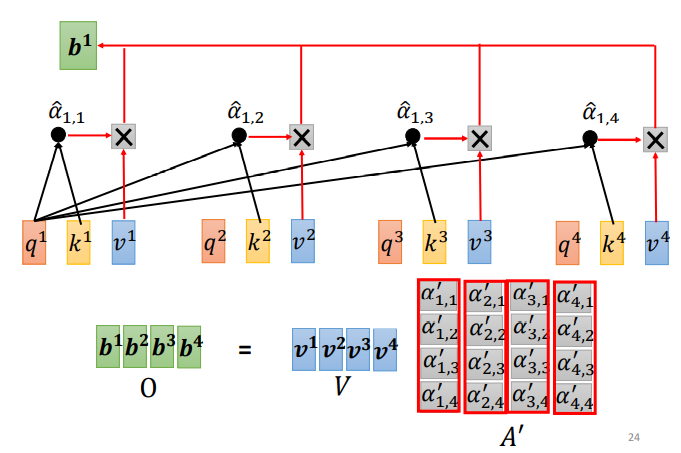
First, calculate v, which is the key value. v is calculated in the same way as q and k, using the input a multiplied by the weight matrix W. After obtaining v, multiply it with the corresponding α′. Each v multiplied by α’ is summed to obtain the output b1.
If a1 and a2 have a high correlation, then α1,2′ will be relatively large. Thus, the output b1 will likely be close to v2, meaning the attention score determines the contribution of that vector in the result;
3.2 Matrix Form
Expressing the generation of b1 using matrix operations:
Step 1: Generate matrices for q, k, and v:
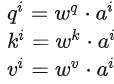
Written in matrix form:
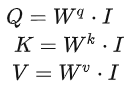
The four inputs a are combined into a matrix with four columns, from a1 to a4, multiplied by the corresponding weight matrix W to obtain the resulting matrices Q, K, and V, representing query, key, and value respectively.
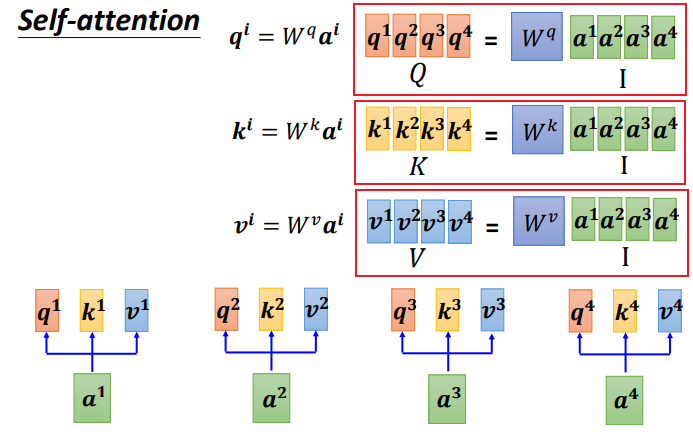
The three Ws are the parameters we need to learn.
Step 2: Using the obtained Q and K to calculate the correlation between each pair of input vectors, which is the calculation of the attention value α. There are various methods to calculate α, usually using the dot product method.
First, for q1, multiply it with the matrix K formed by concatenating k1 to k4 to obtain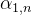
the concatenated matrix.
Similarly, q1 to q4 can also be concatenated into a matrix Q and directly multiplied with matrix K:
The formula is:
In matrix form:
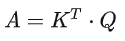
Each value in matrix A records the attention size α between the corresponding two input vectors, and A’ is the matrix after softmax normalization.
Step 3: Using the obtained A’ and V, calculate the output vector b corresponding to each input vector a in the self-attention layer:
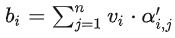
Written in matrix form:
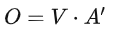
To summarize the self-attention operation process, the input is I, and the output is O:
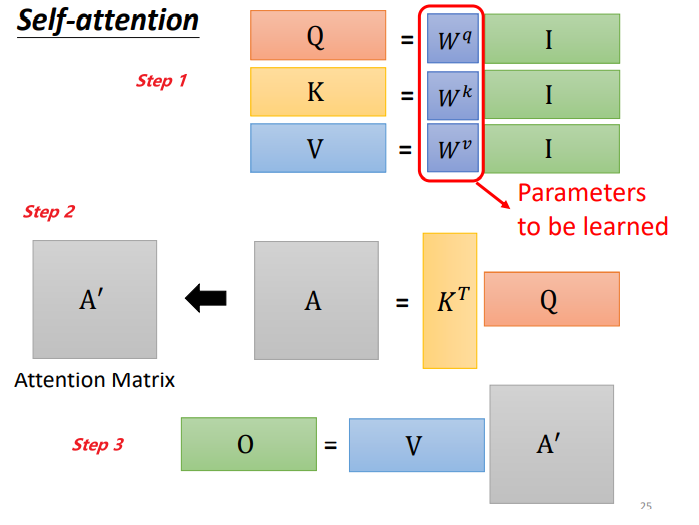
The matrices Wq, Wk, and Wv are the parameters that need to be learned.
4. Multi-head Self-attention
The advanced version of self-attention is Multi-head Self-attention. The multi-head self-attention mechanism.
Since there are many different forms of correlation and many different definitions, sometimes there cannot be just one q; there should be multiple q’s, each responsible for different types of correlation.
For one input a.
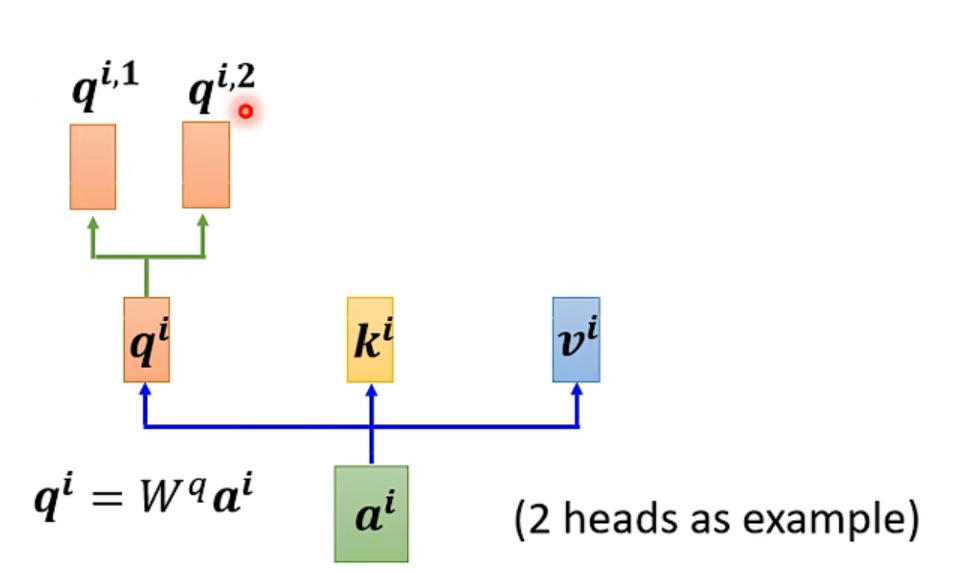
First, similar to above, multiply a by the weight matrix W to obtain q, then use two different Ws to obtain two different q’s, where i represents the position, and 1 and 2 represent the first and second q of that position.
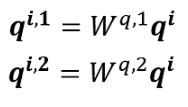
This image shows two heads representing two different types of correlation for this problem.
Similarly, k and v also need to have multiple instances; two k’s and v’s are calculated similarly to q, first calculating ki and vi, then multiplying by two different weight matrices.
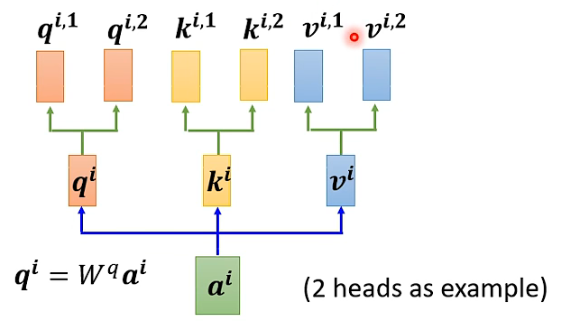
For multiple input vectors, each vector will also have multiple heads:
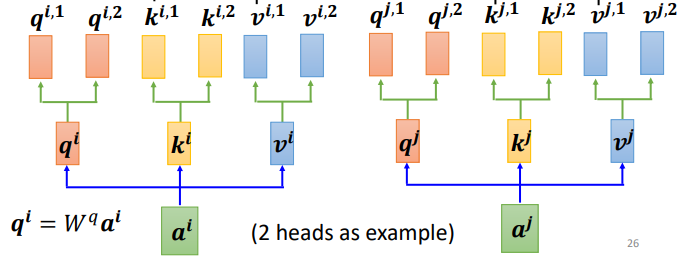
After calculating q, k, and v, how to perform self-attention?
It follows the same process as described above, but the calculations for type 1 are done together, and type 2 is done together, resulting in two independent processes and two outputs b.
For type 1:
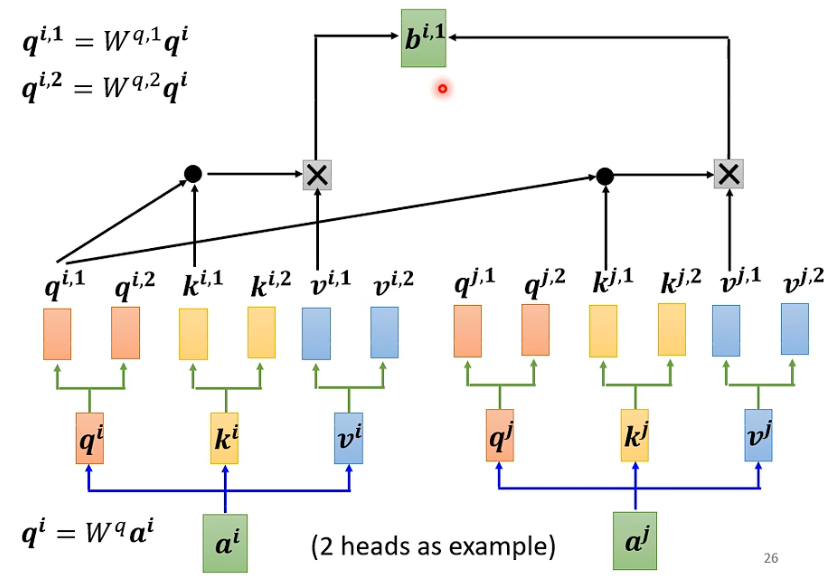
For type 2:
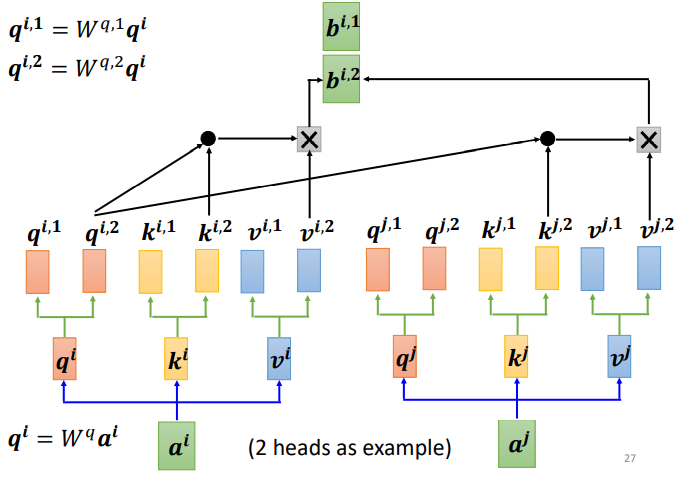
This is just an example of two heads; the process for multiple heads is the same, where b is calculated separately.
5. Positional Encoding
When training self-attention, the information about position is actually missing; there is no distinction between before and after. The above-mentioned a1, a2, a3 do not represent the order of inputs but merely indicate the number of input vectors, unlike RNN, where there is a clear order for inputs. For example, in translation tasks, “machine learning” is input sequentially. However, the input to self-attention is processed simultaneously, and the output is also produced simultaneously.
How can positional information be reflected in Self-Attention? This is done using Positional Encoding.
If ai adds ei, it will reflect the positional information, where i indicates the position.
The length of the vector is set manually, but it can also be trained from data.
6. Differences Between Self-Attention and RNN
The main differences between Self-Attention and RNN are:
1. Self-attention can consider all inputs, while RNN seems to only consider previous inputs (to the left). However, this issue can be avoided when using bidirectional RNN.
2. Self-attention can easily consider inputs from a long time ago, while the earliest inputs in RNN become difficult to consider due to processing through many layers of the network.
3. Self-attention can be computed in parallel, while RNN has a sequential dependency between different layers.
1. Self-attention can consider all inputs, while RNN seems to only consider previous inputs (to the left). However, this issue can be avoided when using bidirectional RNN.
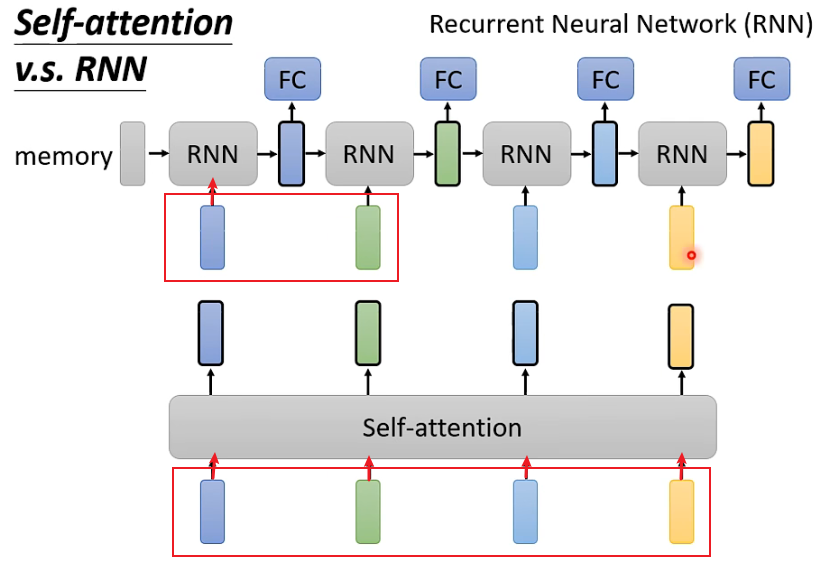
For example, the first RNN only considers the deep blue input, while the green and subsequent inputs are not considered. In contrast, Self-Attention considers all four inputs.
2. Self-attention can easily consider inputs from a long time ago, while the earliest inputs in RNN become difficult to consider due to processing through many layers of the network.
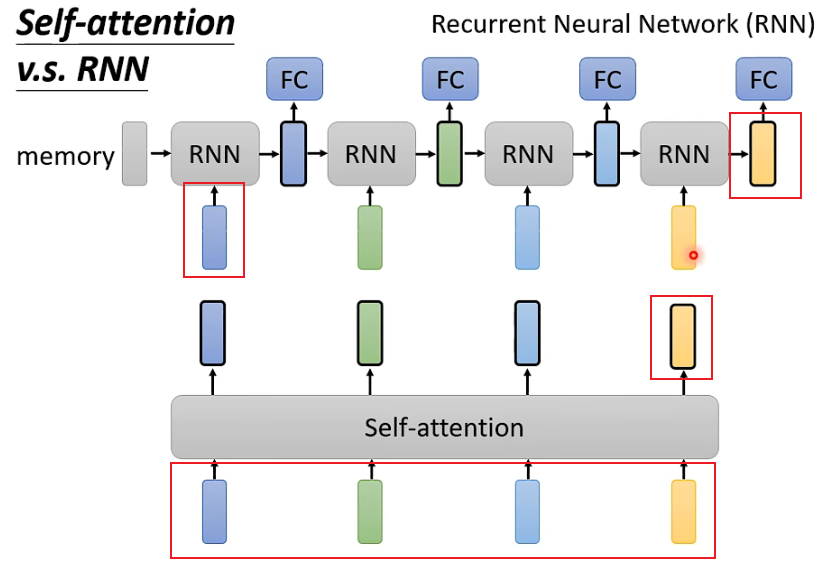
For example, for the last yellow output of RNN, to include the earliest blue input, it must ensure that the blue input does not lose information through each layer. However, if a sequence is very long, it becomes challenging to guarantee this. In contrast, Self-attention directly relates each output to all inputs.
3. Self-attention can be computed in parallel, while RNN has a sequential dependency between different layers.
The input to Self-attention is processed simultaneously, and the output is also produced simultaneously.
Editor: Yu TengkaiProofreader: Wang Xin