This article introduces the main differences between various optimization algorithms and how to choose the best optimization method.
What Are Optimization Algorithms?
The function of optimization algorithms is to minimize (or maximize) the loss function E(x) by improving the training method.
Some internal parameters of the model are used to calculate the deviation between the true value Y and the predicted value in the test set, based on these parameters, the loss function E(x) is formed.
For example, weights (W) and biases (b) are such internal parameters, generally used to calculate the output value and play a major role when training neural network models.
When effectively training the model and producing accurate results, the internal parameters of the model play a very important role. This is why we should use various optimization strategies and algorithms to update and calculate the network parameters that affect model training and model output, bringing them closer to or achieving optimal values.
Optimization algorithms are divided into two main categories:
1. First-order Optimization Algorithms
This type of algorithm uses the gradient values of each parameter to minimize or maximize the loss function E(x). The most commonly used first-order optimization algorithm is Gradient Descent.
Function gradient: The multivariable expression of the derivative dy/dx, used to represent the instantaneous rate of change of y with respect to x. Often, to calculate the derivative of a multivariable function, the gradient is used instead of the derivative, and partial derivatives are used to compute the gradient. A major difference between gradients and derivatives is that the gradient of a function forms a vector field.
Therefore, for single-variable functions, derivatives are used for analysis; while gradients are produced based on multivariable functions. More theoretical details will not be explained here.
2. Second-order Optimization Algorithms
Second-order optimization algorithms use second derivatives (also known as Hessian methods) to minimize or maximize the loss function. Due to the high computational cost of second derivatives, this method is not widely used.
Detailed Explanation of Various Neural Network Optimization Algorithms
Gradient Descent
In training and optimizing intelligent systems, gradient descent is one of the most important techniques and foundations. The function of gradient descent is:
By finding the minimum value, controlling variance, updating model parameters, and ultimately making the model converge.
The formula for updating network parameters is: θ=θ−η×∇(θ).J(θ) , where η is the learning rate, and ∇(θ).J(θ) is the gradient of the loss function J(θ).
This is the most commonly used optimization algorithm in neural networks.
Today, gradient descent is mainly used for weight updates in neural network models, that is, updating and adjusting model parameters in one direction to minimize the loss function.
The introduction of backpropagation technology in 2006 made training deep neural networks possible. Backpropagation calculates the product of input signals and their corresponding weights during forward propagation, then applies the activation function to the sum of these products. This method of transforming input signals into output signals is an important means of modeling complex nonlinear functions and introduces nonlinear activation functions, allowing the model to learn almost any form of function mapping. Then, during the backpropagation of the network, the relevant errors are backpropagated, using gradient descent to update the weight values by calculating the gradient of the error function E with respect to the weight parameters W, updating the weight parameters in the opposite direction of the gradient of the loss function.
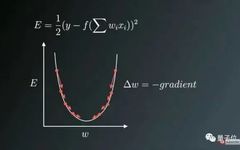
Figure 1: Weight Update Direction Opposite to Gradient Direction
Figure 1 shows the weight update process opposite to the direction of the gradient vector error, where the U-shaped curve represents the gradient. It should be noted that when the weight value W is too small or too large, there can be significant errors, requiring updates and optimizations to convert the weights into suitable values, so we try to find a local optimal value in the direction opposite to the gradient.
Variants of Gradient Descent
Traditional batch gradient descent computes the gradient of the entire dataset but only performs one update, making it slow and difficult to control when dealing with large datasets, even leading to memory overflow.
The speed of weight updates is determined by the learning rate η, and it can converge to a global optimal value in convex error surfaces, while it may approach local optimal values in non-convex surfaces.
Using the standard form of batch gradient descent also has the issue of redundant weight updates when training large datasets.
The above issues with standard gradient descent are resolved in the stochastic gradient descent method.
1. Stochastic Gradient Descent (SGD)
Stochastic gradient descent (SGD) updates parameters for each training sample, performing an update with each execution, and is faster.
θ=θ−η⋅∇(θ) × J(θ;x(i);y(i)), where x(i) and y(i) are the training samples.
Frequent updates result in high variance among parameters, and the loss function will fluctuate with different intensities. This is actually a good thing, as it helps us discover new and possibly better local minima, while standard gradient descent will only converge to a certain local optimal value.
However, the problem with SGD is that due to the frequent updates and fluctuations, it will eventually converge to a minimum limit and may experience overshooting due to frequent fluctuations.
It has been shown that when the learning rate η is gradually reduced, the convergence pattern of standard gradient descent is the same as that of SGD.
Figure 2: High Variance Parameter Updates in Each Training Sample May Cause Significant Fluctuations in the Loss Function, Hence We May Not Obtain the Minimum Value of the Loss Function.
Another variant called Mini-batch Gradient Descent can solve the issues of high variance parameter updates and unstable convergence.
2. Mini-batch Gradient Descent
To avoid the issues present in SGD and standard gradient descent, an improved method is mini-batch gradient descent, which only performs one update for n training samples in each batch.
The advantages of using mini-batch gradient descent are:
1) It can reduce the fluctuations in parameter updates, ultimately achieving better and more stable convergence.
2) It can also utilize common matrix optimization methods in the latest deep learning libraries, making the computation of gradients for mini-batch data more efficient.
3) Generally, the size of mini-batch samples ranges from 50 to 256, which may vary based on the actual problem.
4) When training neural networks, mini-batch gradient descent is usually chosen.
This method is sometimes still referred to as SGD.
Challenges Faced When Using Gradient Descent and Its Variants
1. It is difficult to select an appropriate learning rate. A learning rate that is too small can lead to slow convergence, while a learning rate that is too large may affect convergence and cause the loss function to fluctuate around the minimum value, or even lead to gradient divergence.
2. Furthermore, the same learning rate is not suitable for all parameter updates. If the training data is sparse and the feature frequencies are very different, they should not all be updated to the same extent; rather, features that occur infrequently should use larger update rates.
3. Another key challenge in minimizing non-convex error functions in neural networks is avoiding getting stuck in multiple other local minima. In reality, the problem is not due to local minima, but arises from saddle points, which are points that slope up in one dimension and down in another. These saddle points are often surrounded by planes with the same error value, making it difficult for the SGD algorithm to escape, as the gradient approaches zero in all dimensions.
Further Optimizing Gradient Descent
Now we will discuss various algorithms used to further optimize gradient descent.
1. Momentum
The high variance oscillation in the SGD method makes it difficult for the network to converge stably, so researchers proposed a technique called momentum, which speeds up SGD training by optimizing the training in relevant directions and weakening oscillations in irrelevant directions. In other words, this new method adds the component ‘γ’ of the update vector from the previous step to the current update vector.
V(t)=γV(t−1)+η∇(θ).J(θ)
Finally, parameters are updated through θ=θ−V(t).
The momentum term γ is usually set to 0.9, or a similar value.
The momentum here is consistent with the momentum in classical physics, like throwing a ball from a hill, where the ball collects momentum as it falls, and its speed continues to increase.
The principle is similar in the parameter update process:
1) It enables the network to converge more optimally and stably;
2) It reduces oscillations.
When the gradient points in the actual direction of movement, the momentum term γ increases; when the gradient points in the opposite direction of movement, γ decreases. This means that the momentum term updates parameters only for relevant samples, reducing unnecessary parameter updates, leading to faster and more stable convergence, and reducing oscillation processes.
2. Nesterov Accelerated Gradient
A researcher named Yurii Nesterov noted a problem with the momentum method:
If a ball rolls down a slope blindly, it is very inappropriate. A smarter ball should be aware of where it is going, so when it starts sloping up again, the small ball should slow down.
In fact, when the small ball reaches the lowest point on the curve, the momentum is quite high. High momentum can cause it to completely miss the minimum value, so the ball does not know when to slow down and continues to move upward.
Yurii Nesterov published a paper in 1983 addressing the momentum issue, and thus, we call this method Nesterov’s accelerated gradient.
In this method, he proposed to first make a large leap based on the previous momentum, then calculate the gradient for correction, thus achieving parameter updates. This pre-update method can prevent large oscillations and avoid missing the minimum value, making the parameter updates more sensitive.
Nesterov’s accelerated gradient (NAG) is a method that endows the momentum term with predictive capability by using the momentum term γV(t−1) to modify the parameters θ. By calculating θ−γV(t−1), we obtain an approximate value of the next parameter location, where the parameter is a rough concept. Thus, we do not calculate the gradient of the current parameter θ, but effectively predict the future based on the rough future position of the relevant parameters.
V(t)=γV(t−1)+η∇(θ)J( θ−γV(t−1) ), then use θ=θ−V(t) to update parameters.
Now, we adjust and update the corresponding parameters according to the importance of each parameter, enabling larger or smaller update amplitudes.
3. Adagrad Method
The Adagrad method adjusts the appropriate learning rate η based on parameters, making large updates for sparse parameters and small updates for frequent parameters. Therefore, the Adagrad method is very suitable for handling sparse data.
In each time step, the Adagrad method sets different learning rates for different parameters θ based on the past gradients calculated for each parameter.
Previously, each parameter θ(i) used the same learning rate, and all parameters θ were updated each time. In each time step t, the Adagrad method selects different learning rates for each parameter θ, updates the corresponding parameters, and then vectorizes. For simplicity, we denote the gradient of the loss function of parameter θ(i) at time t as g(t,i).
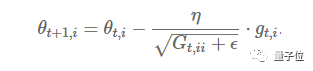
Figure 3: Parameter Update Formula
The Adagrad method modifies the corresponding learning rate η for each parameter θ(i) based on previously computed gradients in each time step.
The main advantage of the Adagrad method is that it does not require manual adjustment of the learning rate. Most parameters use a default value of 0.01, which remains unchanged.
The main disadvantage of the Adagrad method is that the learning rate η continuously decreases and decays.
Because each additional term is positive, the accumulated sum of squared gradients in the denominator keeps increasing during training. This, in turn, leads to a decrease in the learning rate, turning into a very small number, causing the model to completely stop learning and stop acquiring new knowledge.
As the learning speed decreases, the model’s learning ability rapidly diminishes, and the convergence speed is very slow, requiring a long time for training and learning, that is, reduced learning speed.
Another algorithm called Adadelta improves the issue of the continuously decaying learning rate.
4. AdaDelta Method
This is an extension of the AdaGrad method that tends to solve its learning rate decay problem. Adadelta does not accumulate all previous squared gradients, but limits the accumulation of previous gradients to a fixed window size w.
Unlike the previous ineffective storage of prior squared gradients, the sum of gradients is defined recursively as the exponentially decaying average of all previous squared gradients. Similar to the momentum term, the sliding average Eg² at time t only depends on the previous average and the current gradient value.
Eg²=γ.Eg²+(1−γ).g²(t), where γ is set to a value close to the momentum term, around 0.9.
Δθ(t)=−η⋅g(t,i).
θ(t+1)=θ(t)+Δθ(t)

Figure 4: Final Formula for Parameter Updates
Another advantage of the AdaDelta method is that there is no need to set a default learning rate.
Improvements Made So Far
1) Different learning rates are calculated for each parameter;
2) The momentum term has also been calculated;
3) Prevent issues such as learning rate decay or gradient vanishing.
What Further Improvements Can Be Made?
In previous methods, the corresponding learning rates for each parameter were calculated, but why not calculate the corresponding momentum changes for each parameter and store them independently? This is the improvement point proposed by the Adam algorithm.
Adam Algorithm
The Adam algorithm, which stands for Adaptive Moment Estimation, can calculate adaptive learning rates for each parameter. This method not only stores the exponentially decaying average of the previous squared gradients of AdaDelta but also maintains the exponentially decaying average of the previous gradients M(t), similar to momentum:
M(t) is the first moment average of the gradient, and V(t) is the second moment non-central variance.
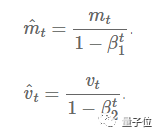
Figure 5: The Two Formulas Represent the First Moment Average of the Gradient and the Second Moment Variance
Then the final formula for parameter updates is:
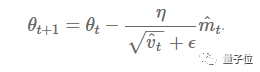
Figure 6: Final Formula for Parameter Updates
Where β1 is set to 0.9, β2 is set to 0.9999, and ϵ is set to 10-8.
In practical applications, the Adam method performs well. Compared to other adaptive learning rate algorithms, it converges faster, learns more effectively, and can correct issues present in other optimization techniques, such as vanishing learning rates, slow convergence, or high variance parameter updates leading to significant fluctuations in the loss function.
Visualizing Optimization Algorithms
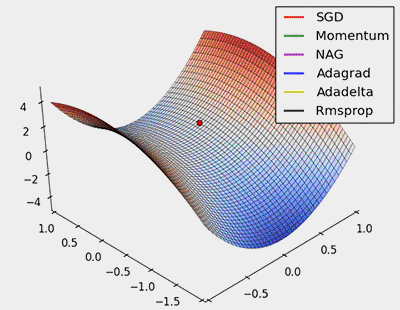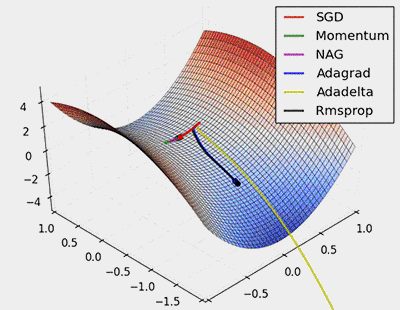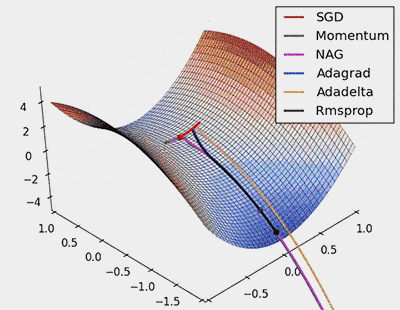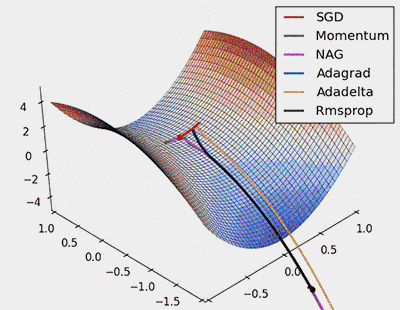
Figure 7: SGD Optimization on Saddle Points
From the animation above, it can be seen that adaptive algorithms can converge quickly and find the correct target direction in parameter updates; while standard SGD, NAG, and momentum methods converge slowly and find it difficult to locate the correct direction.
Conclusion
Which optimizer should we use?
When constructing neural network models, it is important to select the best optimizer to achieve rapid convergence and accurate learning, while adjusting internal parameters to minimize the loss function as much as possible.
In practical applications, Adam performs well, surpassing other adaptive techniques.
If the input dataset is relatively sparse, methods like SGD, NAG, and momentum may not perform well. Therefore, for sparse datasets, some adaptive learning rate method should be used, and another benefit is that there is no need for manual adjustment of the learning rate; using default parameters may yield optimal values.
If you want to quickly converge deep network models or if the constructed neural network is relatively complex, then you should use Adam or other adaptive learning rate methods, as these methods perform better in practice.
We hope this article helps you understand the differences in characteristics among different optimization algorithms.
Related Links:
Second-order Optimization Algorithms: https://web.stanford.edu/class/msande311/lecture13.pdf
Nesterov’s Accelerated Gradient: http://cs231n.github.io/neural-networks-3/
Text / Southern
Images / Southern
Layout / Southern
Click below
Follow us