【Introduction】This article provides the background and overview of Dropout, as well as a parameter analysis of its application in language modeling using LSTM / GRU recurrent neural networks.
Author|Adrian G
Compiler|Zhuanzhi (No secondary reproduction), Xiaoshi
Organizer|Yingying
Dropout
Inspired by the role of gender in evolution, Hinton et al. first proposed Dropout, which temporarily removes units from the neural network. Srivastava et al. applied Dropout to feedforward neural networks and restricted Boltzmann machines, noting that a dropout rate of 0.5 for hidden layers and 0.2 for input layers is suitable for various tasks.
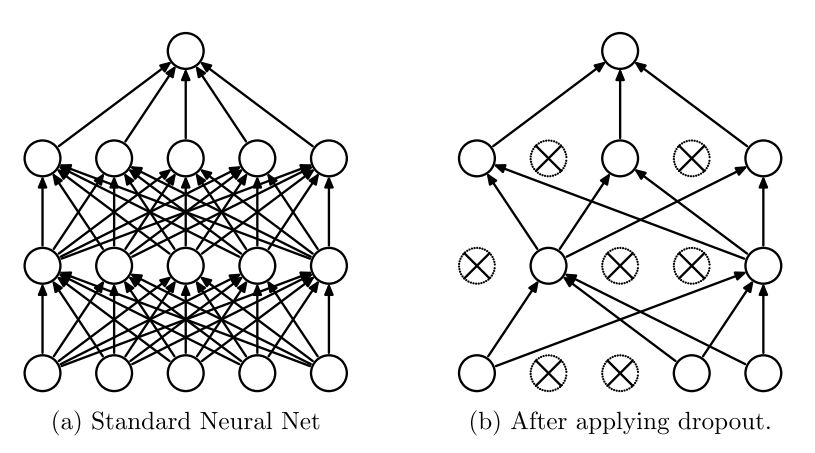
Figure 1. (a) Standard neural network without dropout. (b) Neural network with dropout applied.
The core concept of Srivastava et al.’s work is that “in a neural network with dropout, each hidden unit must learn to randomly select samples from other units during training. This should make each hidden unit more robust and drive it to learn useful features without relying on other hidden units to correct its errors.” In standard neural networks, each parameter is gradually optimized to reach a global minimum through gradient descent. As a result, hidden units may update parameters to correct the errors of other units. This can lead to “co-adaptation,” which in turn can result in overfitting. By making the presence of other hidden units unreliable, dropout prevents co-adaptation of each hidden unit.
For each training sample, the network is reconfigured, and a new set of neurons is dropped. During testing, the weights need to be multiplied by the dropout rate of the relevant units.

Figure 2. (a) Error when the number of hidden units (n) is fixed (2) after dropout with a fixed number of hidden units.
We can see in Figure 2a that the test error remains stable when the probability of keeping neurons (1-dropout) is between 0.4 and 0.8. As the dropout rate falls below 0.2 (P> 0.8), the test error increases. When the dropout rate is too high (p <0.3), the network underfits.
Srivastava et al. further found that “as the dataset grows, the benefit of dropout increases to a point and then decreases. This indicates that there exists an ‘optimal point’ for any given network structure and dropout rate.”
Srivastava et al. represented the probability of hidden units being activated using Bernoulli, where the value is 1 with probability p, otherwise 0.
Example code for dropout is as follows:
class Dropout():
def __init__(self, prob=0.5):
self.prob = prob
self.params = []
def forward(self,X):
self.mask = np.random.binomial(1,self.prob,size=X.shape) / self.prob
out = X * self.mask
return out.reshape(X.shape)
def backward(self,dout):
dX = dout * self.mask
return dX,[]DropConnect
After Dropout, Wan et al. further proposed DropConnect, which “extends Dropout by randomly dropping weights instead of activations.” “With DropConnect, what is dropped is each connection, not each output unit.” Like Dropout, this technique only applies to fully connected layers.

Figure 3. (a) Example model layout of a single DropConnect layer. After running the feature extractor g() on input x, a mask M is randomly instantiated (for example (b). The masked weights are multiplied by this feature vector to produce u, which is the input to the activation function a and softmax layer s. For comparison, c) shows the effective weight mask used when Dropout is applied to the output (column) of the previous layer and the output (row) of this layer.
As shown in the figure below, we can illustrate the difference between Dropout and DropConnect. By applying dropout to the input weights instead of activations, DropConnect can generalize to the entire connection structure of fully connected network layers.

Figure 4. Neurons take a series of weights as input and apply a nonlinear activation function to generate output.
The two dropout methods mentioned above are applied to feedforward convolutional neural networks. The difference between RNN and only feedforward neural networks is that the previous state is fed back into the network, allowing the network to retain previous states. Therefore, applying standard dropout to RNN limits the network’s ability to retain previous states, hindering its performance. Bayer et al. pointed out the problem of applying dropout to recurrent neural networks (RNNs). Setting the entire output weight vector to zero “causes significant dynamic changes in the RNN during each forward pass.”

Figure 5. Examples of regular feedforward and (feedforward) convolutional neural networks (ConvNet).

Figure 6. Applying dropout in RNNs

Figure 7. The above model unfolds after RNN
Code for applying Dropout in RNN
class RNN:
# ...
def step(self, x):
# update the hidden state
self.h = np.tanh(np.dot(self.W_hh, self.h) + np.dot(self.W_xh, x))
# compute the output vector
y = np.dot(self.W_hy, self.h)
return y
rnn = RNN()
y = rnn.step(x) # x is an input vectorDropout in RNNs
As a method to overcome the performance issues of dropout applied to RNNs, Zaremba and Pham et al. only apply dropout to non-recurrent connections (Dropout is not applied to hidden states). “By not using dropout on recurrent connections, LSTM can benefit from dropout regularization without sacrificing its valuable memory capabilities.”

Figure 8. Regularizing multi-layer RNN. Dropout is only applied to non-recurrent connections (i.e., only applied to feedforward dashed lines). The thick line shows the typical information flow path in LSTM. The information is affected by dropout L + 1 times, where L is the depth of the network.
Variational Dropout
Gal and Ghahramani (2015) analyzed the application of Dropout to only feedforward RNNs and found that this approach still leads to overfitting. They proposed “Variational Dropout,” which uses the same dropout mask for each time step of the input, output, and recurrent layers (dropping the same network units at each time step). Using a Bayesian interpretation, they observed improvements in language modeling and sentiment analysis tasks over ‘pure dropout.’
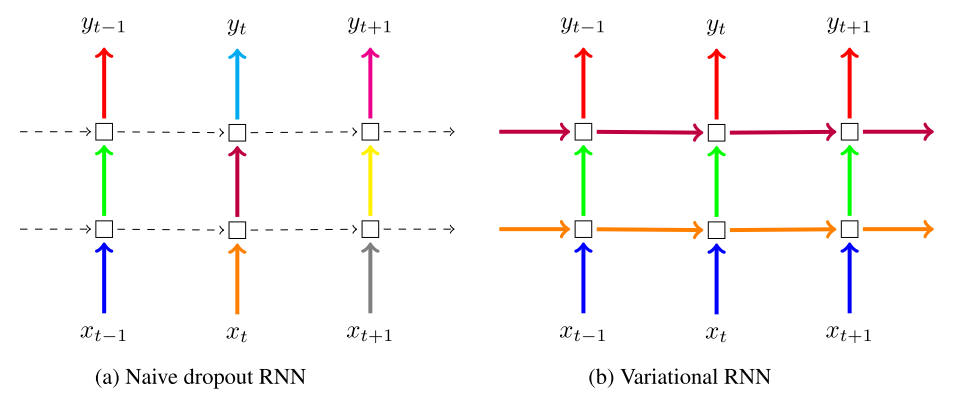
Figure 9. Naive dropout (a) uses different masks at different time steps, with no dropout on recurrent layers. Variational dropout (b) uses the same dropout mask at each time step, including recurrent layers (color indicates Dropout mask, solid line indicates dropout, dashed line indicates standard connections without dropout).
Recurrent Dropout
Similar to Moon and Gal and Ghahramani, Semeniuta et al. proposed applying dropout to the recurrent connections of RNNs so that the recurrent weights could be regularized for performance improvement. Gal and Ghahramani used the hidden state of the network to compute gate values and cell updates, and used the hidden state as input to the subnetwork with dropout (Figure 9b). The difference with Semeniuta et al. is that they believe “the entire architecture is key to the hidden state and regularizes the entire network.” This is similar to the concept of Moon et al. (as shown in Figure 9a), but Semeniuta et al. found that directly dropping the previous state according to Moon et al. produced mixed results, while applying dropout to the hidden state update vector is a more principled approach.

“Our technique allows for the addition of strong regularizers on model weights responsible for learning short-term and long-term dependencies, without affecting the ability to capture long-term relationships, which is particularly important for models dealing with natural language.”

Figure 10. Semeniuta et al. “Illustration of three types of dropout in the recurrent connections of LSTM networks. Dashed arrows indicate broken connections. For clarity, input connections are omitted.” Note how Semeniuta et al. (2016) applied repeated dropout to the updates of LSTM memory cells.
“We demonstrate that recurrent dropout is most effective when applied to the hidden state update vector rather than the hidden state; (ii) when our recurrent dropout rate is combined with the standard forward dropout rate, we observe improvements in network performance, although the degree of this improvement depends on the value of the dropout rate; (iii) contrary to our expectations, networks trained using our recurrent dropout method with stepwise and sequential mask sampling produce similar results, both outperforming the dropout scheme proposed by Moon et al.
Zoneout
As a variant of dropout, Krueger et al. proposed Zoneout, which “does not set the activation of certain units to zero; instead, Zoneout randomly replaces the activation of certain units with their activation from the previous time step.” This “makes it easier for the network to retain information from previous time steps as it progresses, facilitating rather than hindering the flow of gradient information backward.”

Figure 11. Zoneout as a special case of dropout; ~ht is the hidden activation of unit h at the next time step (if no partition). Zoneout can be seen as applying dropout on the hidden state increment, ~ht – ht-1. When this update is removed (as indicated by the dashed line), ht becomes ht-1.
While both recurrent dropout and Zoneout prevent the loss of long-term memory established in GRUs / LSTMs, “zoneout achieves this by precisely retaining the activation of units. This difference is most pronounced when partitioning the hidden state of LSTMs (not the memory cell) since there is no similar recurrent dropout in LSTMs. Saturated output gates or output nonlinearities can lead to gradient vanishing in repeated dropout, whereas Zoneout effectively propagates gradients. Furthermore, while recurrent dropout methods are specific to LSTMs and GRUs, zoneout generalizes to any model that sequentially builds its input’s distributed representation, including naive RNNs.”

Figure 12. (a) Zoneout, compared with (b) recurrent dropout strategy in LSTM. Dashed lines indicate zero masks; in zoneout, the corresponding dashed line covers the respective opposite zero mask. Rectangular nodes are embedding layers.
Core idea of implementing Zoneout with TensorFlow
if self.is_training:
new_state = (1 - state_part_zoneout_prob) * tf.python.nn_ops.dropout(
new_state_part - state_part, (1 - state_part_zoneout_prob),
seed=self._seed) + state_part
else:
new_state = state_part_zoneout_prob * state_part
+ (1 - state_part_zoneout_prob) * new_state_partAWD-LSTM
In a pioneering work on RNN regularization for language modeling, Merity et al. proposed a method they called AWD-LSTM. In this approach, Merity et al. used DropConnect on the hidden weight matrix, while all other dropout operations used variational dropout, along with several other regularization strategies including random lengths, backpropagation through time (BPTT), activation regularization (AR), and time activation regularization (TAR).
Regarding DropConnect, Merity et al. mentioned that “since the same weights are reused across multiple time steps, the same weight remains down throughout the forward and backward passes. The result is similar to variational dropout, which applies the same dropout mask to the recurrent connections within the LSTM by performing dropout on ht-1, except that dropout is applied to the recurrent weights.”
Concerning the use of variational dropout, Merity et al. noted that “each example in the mini-batch uses a unique dropout mask, rather than using a single dropout mask across all examples, ensuring diversity of elements.”
Utilizing the embedded dropout by Gal & Ghahramani, Merity et al. also noted that this “corresponds to performing dropout at the word level on the embedding matrix, where dropout is broadcasted across all word vectors in the embedding.” “Since dropout occurs on the embedding matrix used for full forward and backward passes, this means that all occurrences of a specific word will disappear in that pass, equivalent to performing variational dropout on one-hot embeddings and connections in between.”
Code used by Merity et al.:
class LockedDropout(nn.Module):
def __init__(self):
super().__init__()
def forward(self, x, dropout=0.5):
if not self.training or not dropout:
return x
m = x.data.new(1, x.size(1), x.size(2)).bernoulli_(1 - dropout)
mask = Variable(m, requires_grad=False) / (1 - dropout)
mask = mask.expand_as(x)
return mask * xThus, the location of applying the forward method dropout in RNNModel (note self.lockdrop = LockedDropout(mask = mask)):
def forward(self, input, hidden, return_h=False):
emb = embedded_dropout(self.encoder, input, dropout=self.dropoute
if self.training else 0)
emb = self.lockdrop(emb, self.dropouti)
raw_output = emb
new_hidden = []
raw_outputs = []
outputs = []
for l, rnn in enumerate(self.rnns):
current_input = raw_output
raw_output, new_h = rnn(raw_output, hidden[l])
new_hidden.append(new_h)
raw_outputs.append(raw_output)
if l != self.nlayers - 1:
raw_output = self.lockdrop(raw_output, self.dropouth)
outputs.append(raw_output)
hidden = new_hidden
output = self.lockdrop(raw_output, self.dropout)
outputs.append(output)
result = output.view(output.size(0)*output.size(1), output.size(2))
if return_h:
return result, hidden, raw_outputs, outputs
return result, hiddenDropConnect applied to the same RNNModel’s init method:
if rnn_type == 'LSTM':
self.rnns = [torch.nn.LSTM(ninp if l == 0 else nhid,
nhid if l != nlayers - 1
else (ninp if tie_weights else nhid),
1, dropout=0) for l in range(nlayers)]
if wdrop:
self.rnns = [WeightDrop(rnn, ['weight_hh_l0'], dropout=wdrop)
for rnn in self.rnns]The key part of the WeightDrop class is the following method:
def _setweights(self):
for name_w in self.weights:
raw_w = getattr(self.module, name_w + '_raw')
w = None
if self.variational:
mask = torch.autograd.Variable(torch.ones(raw_w.size(0), 1))
if raw_w.is_cuda: mask = mask.cuda()
mask = torch.nn.functional.dropout(mask, p=self.dropout,
training=True)
w = mask.expand_as(raw_w) * raw_w
else:
w = torch.nn.functional.dropout(raw_w, p=self.dropout,
training=self.training)
setattr(self.module, name_w, w)References:
J. Bayer, C. Osendorfer, D. Korhammer, N. Chen, S. Urban, P. van der Smagt. 2013. On Fast Dropout and its Applicability to Recurrent Networks.
Y. Bengio, P. Simard, P. Frasconi. 1994. Learning long-term dependencies with gradient descent is difficult.
cs231n. https://cs231n.github.io/convolutional-networks/
deepnotes.io. https://deepnotes.io/dropout
Y. Gal, abd Z. Ghahramani. 2015. A Theoretically Grounded Application of Dropout in Recurrent Neural Networks.
G. E. Hinton, N. Srivastava, A. Krizhevsky, I. Sutskever and R. R. Salakhutdinov. 2012. Improving neural networks by preventing co-adaptation of feature detectors.
karpathy.github.io. https://karpathy.github.io/2015/05/21/rnn-effectiveness/
D. Krueger, T. Maharaj, J. Kramár, M. Pezeshki, N. Ballas, N. Rosemary Ke, A. Goyal, Y. Bengio, A. Courville, C. Pal. 2016. Zoneout: Regularizing RNNs by Randomly Preserving Hidden Activations.
S. Merity, N. Shirish Keskar, R. Socher. 2017. Regularizing and Optimizing LSTM Language Models.
ml-cheatsheet.readthedocs.io. https://ml-cheatsheet.readthedocs.io/en/latest/nn_concepts.html
T. Moon, H. Choi, H. Lee, I. Song. 2015. Rnndrop: A novel dropout for rnns.
P. Morerio, J. Cavazza, R. Volpi, R.Vidal, V. Murino. 2017. Curriculum Dropout
A. Narwekar, A. Pampari. 2016. Recurrent Neural Network Architectures. http://slazebni.cs.illinois.edu/spring17/lec20_rnn.pdf
V. Pham, T. Bluche, C. Kermorvant, J. Louradour. 2013. Dropout improves Recurrent Neural Networks for Handwriting Recognition
S. Semeniuta, A. Severyn, E. Barth. 2016. Recurrent Dropout without Memory Loss.
N. Srivastava, G. Hinton, A. Krizhevsky, I. Sutskever, R. Salakhutdinov. 2014. Dropout: A Simple Way to Prevent Neural Networks from Overfitting.
L. Wan, M. Zeiler, Matthew, S. Zhang, Y. LeCun, R. Fergus. 2013. Regularization of neural networks using dropconnect.
W. Zaremba, I. Sutskever, O. Vinyals. 2014. Recurrent Neural Network Regularization
K. Zolna, D. Arpit, D. Suhubdy, Y. Bengio. 2017. Fraternal Dropout
