In-Depth! Illustrated Mathematical Principles of Neural Networks

Nowadays, after becoming proficient in using dedicated frameworks and high-level libraries like Keras, TensorFlow, or PyTorch, we no longer need to frequently worry about the size of neural network models or remember formulas for activation functions and derivatives. With these libraries and frameworks, creating a neural network, even one with a complex architecture, often only requires a few imports and a few lines of code. Here’s an example:

Building a Neural Network Using a Framework

First, I will demonstrate a popular neural network framework — Keras used for building neural network models.

from keras.models import Sequential
from keras.layers import Dense

model = Sequential()
model.add(Dense(4, input_dim=2, activation='relu'))
model.add(Dense(6, activation='relu'))
model.add(Dense(6, activation='relu'))
model.add(Dense(4, activation='relu'))
model.add(Dense(1, activation='sigmoid'))

model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X_train, y_train, epochs=50, verbose=0)

As mentioned earlier, just a few imports and a few lines of code can create and train a model that can achieve nearly 100% accuracy in solving classification problems. Our task can be summarized as providing hyperparameters for the model based on the chosen model structure, such as the number of network layers, the number of neurons in each layer, activation functions, and the number of training epochs, etc. Now let’s take a look at what happens during the training process; we can see that the data is correctly separated as the training progresses!

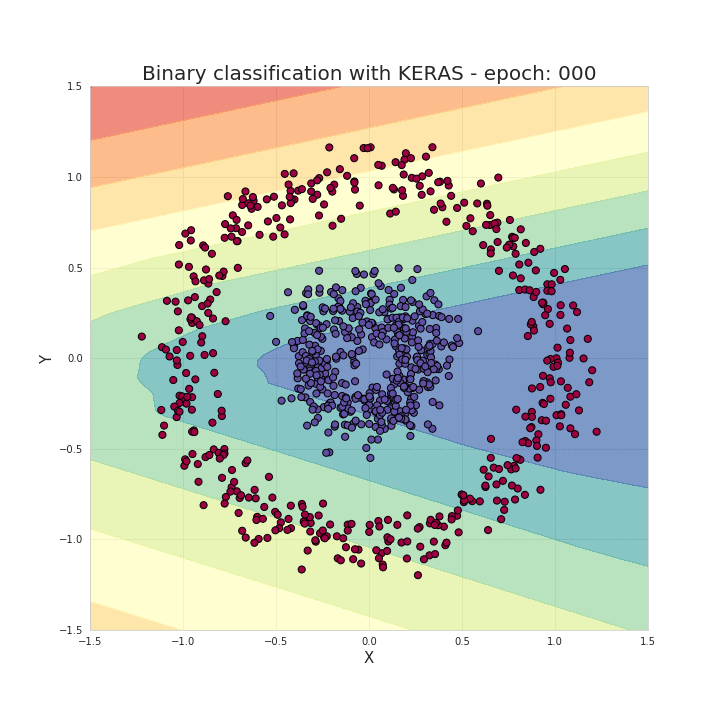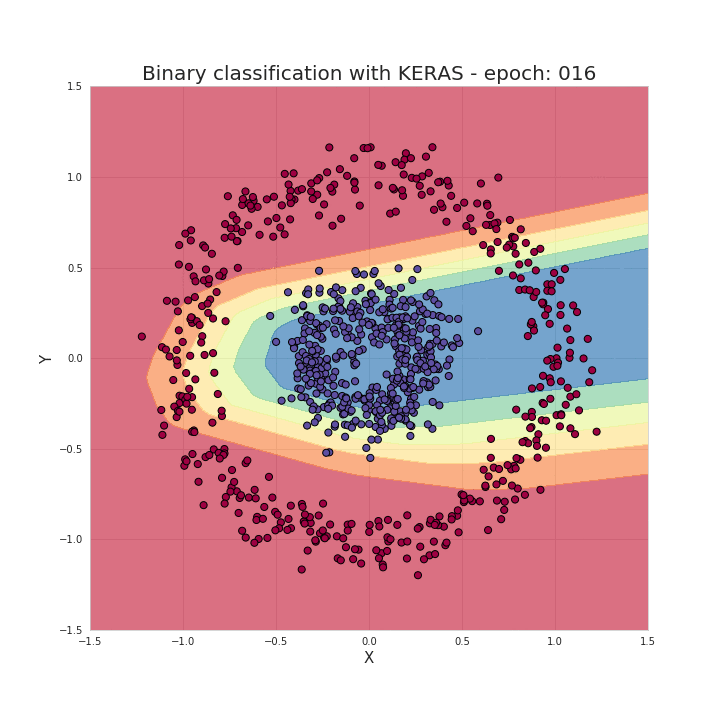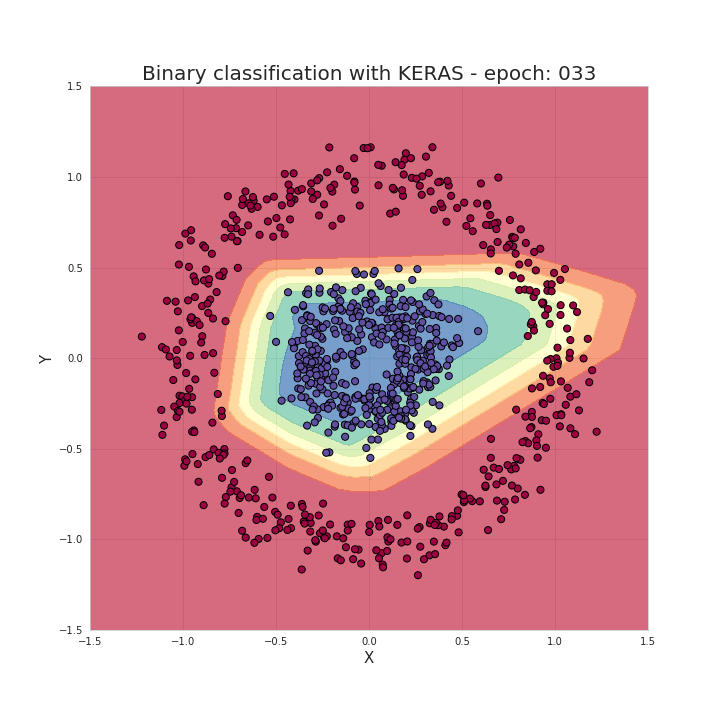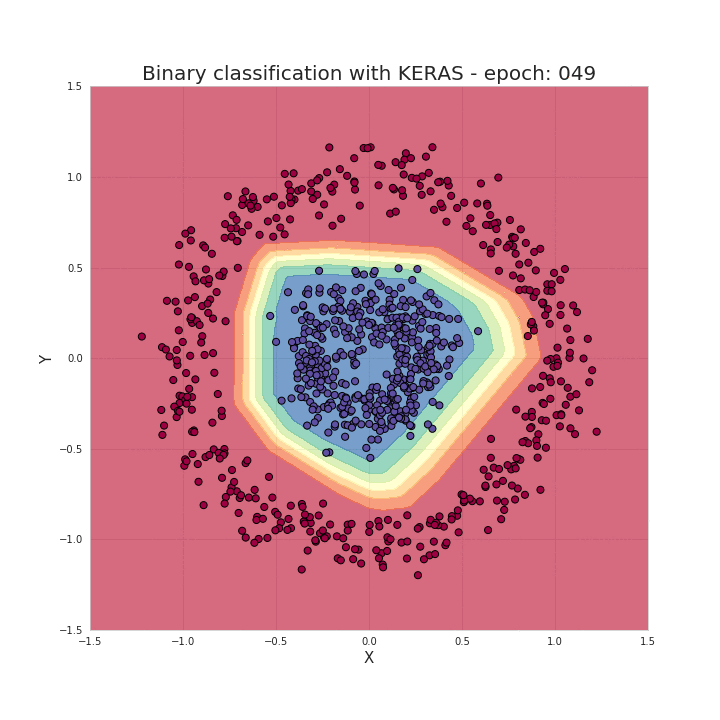
With these frameworks, it indeed saves us a lot of time writing bugs (…) and makes our work more streamlined. However, understanding the working principles behind neural networks is extremely helpful for us in choosing model architectures, tuning parameters, or optimizing models.

Principles of Neural Networks

To gain a deeper understanding of how neural networks work, this article will help everyone understand some concepts that may be confusing during the learning process. I will try to make it less painful for those who are not interested in algebra and calculus, but as the title suggests, this article mainly discusses mathematical principles, so a lot of mathematics will be discussed; just a heads-up.

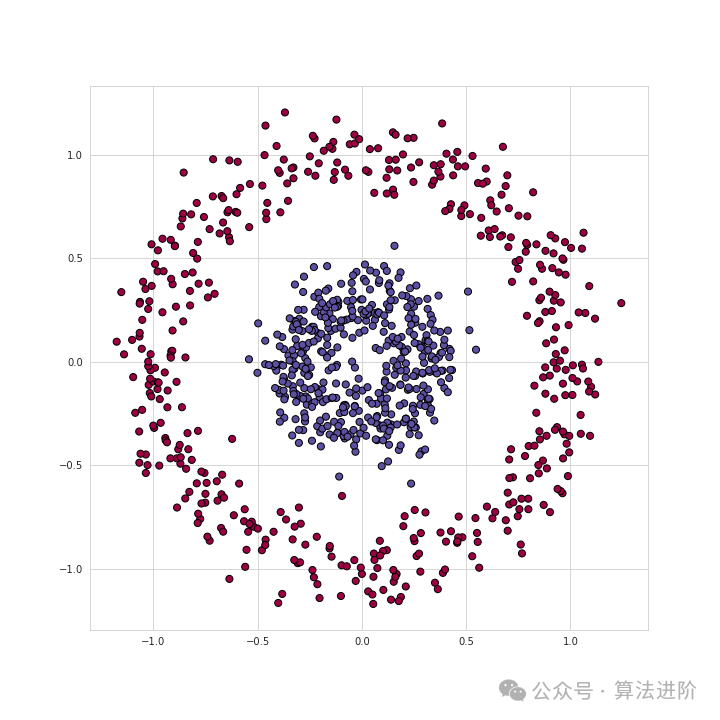
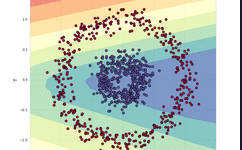
For example, we want to solve a binary classification problem for a dataset, as shown above.

The data points are composed of two categories in circular shapes, and distinguishing this data is very troublesome for many traditional machine learning algorithms, but neural networks can handle this nonlinear classification problem well.

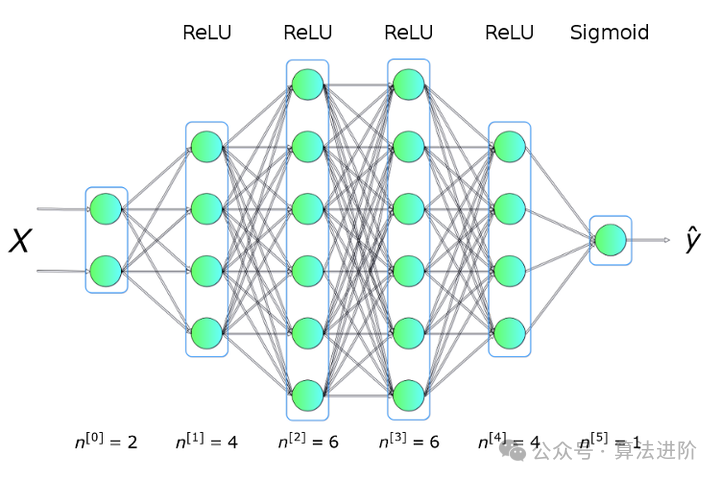
To solve this problem, we will use a neural network structure as shown in the figure below, which has 5 fully connected layers, each with a different number of neurons. For the hidden layers, we will use ReLU as the activation function, and in the output layer, we will use the sigmoid function. This is a fairly simple structure but sufficient to solve our problem.

What is a Neural Network?

First, let’s answer this key question: what is a neural network? It is a computer program created under biological inspiration that can learn knowledge and independently discover relationships in data. As shown in Figure 2, a neural network is a series of neurons arranged in network layers, which are connected in such a way that they can communicate with each other.

Single Neuron

Each neuron receives a series of x values (numbers from 1 to n) as input and calculates the predicted y-hat value. The vector x actually contains the feature values of one sample from the m samples in the training set. Each neuron has its own set of parameters, usually referred to as w (the column vector of weights) and b (bias), which change continuously during the learning process. In each iteration, the neuron calculates its weighted average based on the current weight vector x and adds the bias. Finally, the calculated result is passed to a nonlinear function or function g. I will mention some of the most common activation functions below.

Single Network Layer

Now, let’s narrow down the scope a bit and think about how the entire network layer of the neural network performs mathematical operations. We will use the calculation knowledge of a single neuron to vectorize the calculations across the entire layer and integrate these calculations into matrix equations. To keep the mathematical symbols consistent, these equations will be written for the selected network layer. Additionally, the subscript i symbol marks the order of the neurons in this layer.

Another important thing: when we write equations for a single neuron, we use x and y-hat, which represent the feature column vector and predicted value, respectively. When switching to the general symbols for the network layer, we use the vector a — which means the activation corresponding to that network layer. Thus, the x vector is the activation of network layer 0 (input layer). Each neuron in the network layer performs the same operation according to the following equation:

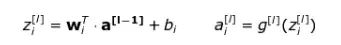
To make it clearer for everyone, let’s write down the formula for the second layer:

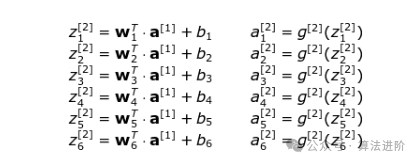
You can see that for each network layer, we must perform a series of very similar calculations. Using a for loop here is not very efficient, so we switch to vectorization to speed up the calculations. First, we stack the horizontal vectors of weights w together to create matrix W. Similarly, we stack the biases of each neuron in the network layer together to create a vertical vector b. Now, we can smoothly create a matrix equation to calculate all neurons in that network layer at once. We also write down the dimensions of the matrices and vectors used.

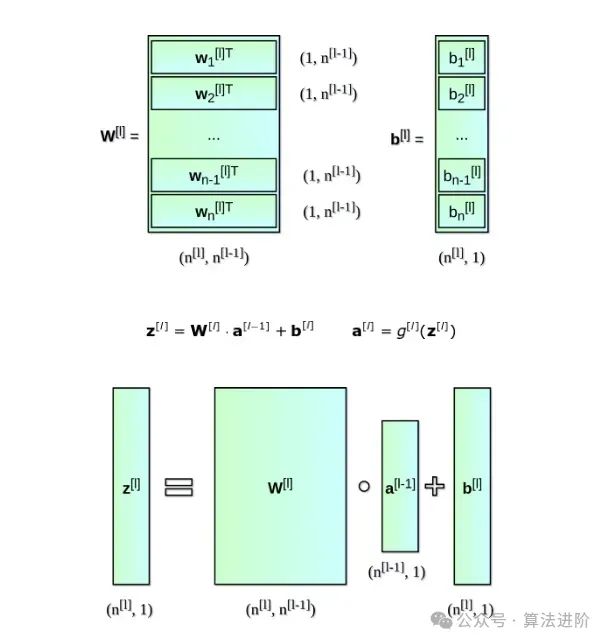
Vectorization in Multiple Examples

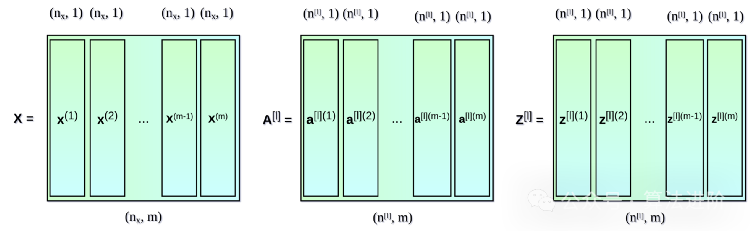
The equations we have used so far only involve one example. In the learning process of neural networks, you usually have to deal with a large amount of data, up to millions of entries. So the next step is to implement vectorization across multiple examples. Suppose our dataset has m entries, each with nx features. First, we will stack the vertical vectors x, a, and z of each layer together to create matrices X, A, and Z, respectively. Then, we will rewrite the previously listed equations based on the newly created matrices.

What is an Activation Function? Why Do We Need It?

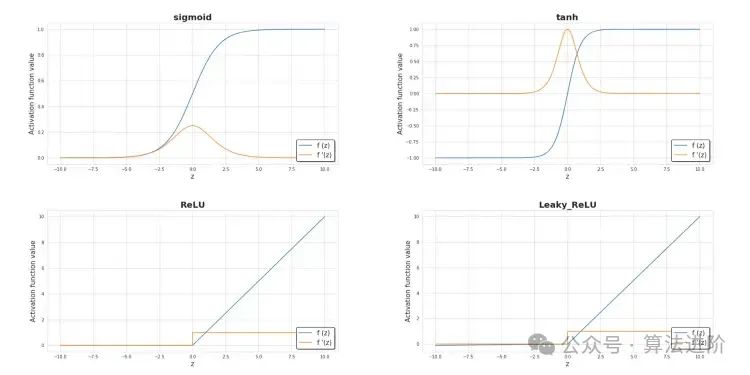
The activation function is one of the most important parts of a neural network.Without an activation function, our neural network would just be a combination of linear functions, which would merely be a linear function. If that were the case, the model’s scalability would be very limited, not much stronger than logistic regression. The nonlinear part allows the model to have greater flexibility and to create complex functions during the learning process.

Moreover, the activation function significantly impacts the learning speed of the model, which is one of the main criteria for selecting a model. The following figure shows some commonly used activation functions. Currently, the most commonly used activation function in hidden layers should be ReLU. When dealing with binary classification problems, especially when we want the model to return values between 0 and 1, we sometimes also use the sigmoid function, especially in the output layer.

Loss Function

The basic information source during the learning process is the value of the loss function. Generally speaking, the purpose of using a loss function is to show the gap between us and the “ideal” situation. In our case, we used binary cross-entropy, but depending on the specific problem we are dealing with, different functions can be used. The function we used is represented by the following formula, and the visualization of its value changes during the learning process is shown in the animated image below. It shows that the value of the loss function decreases continuously with each iteration, and the accuracy value also increases continuously.

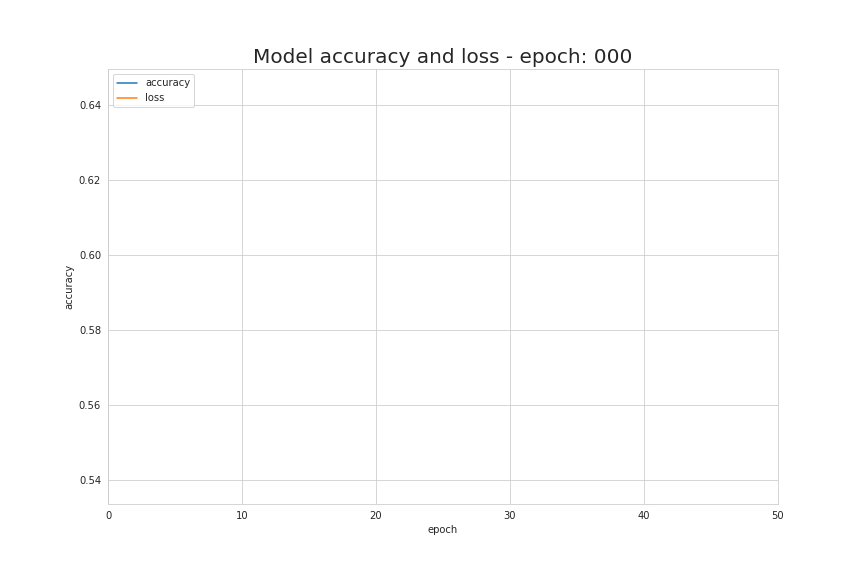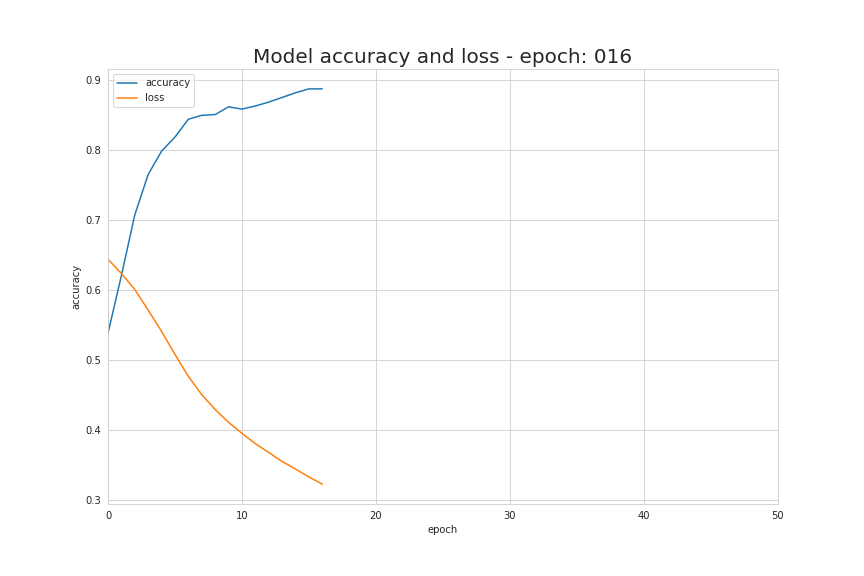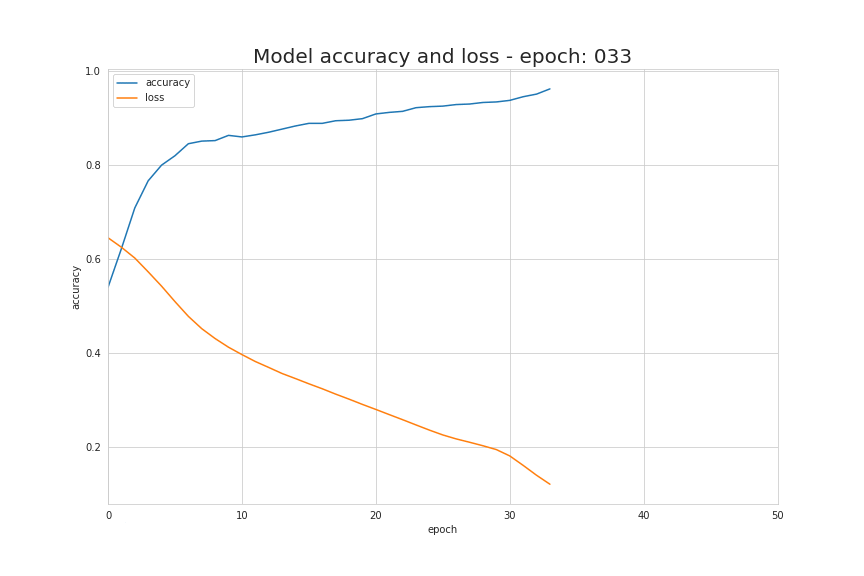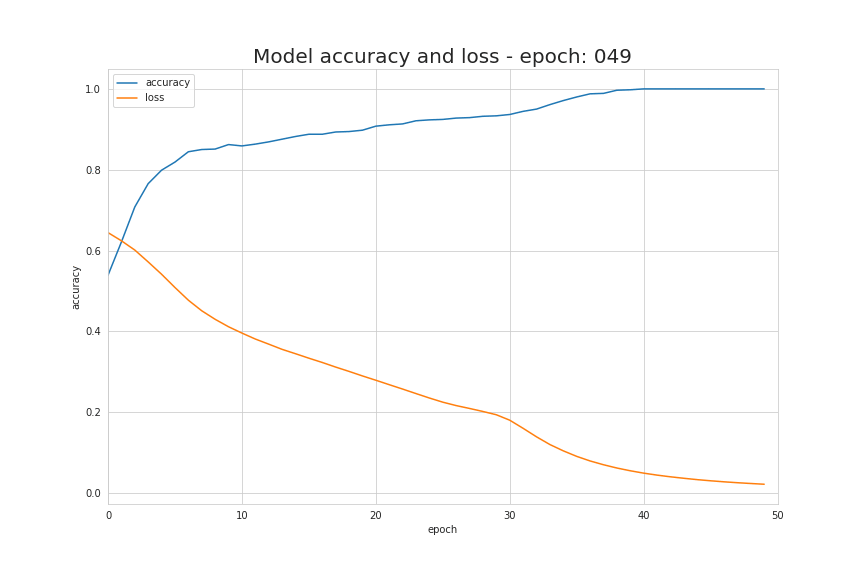
How Do Neural Networks Learn?

The learning process involves continuously changing the values of the parameters W and b to minimize the loss function. To achieve this goal, we use calculus and employ gradient descent to find the minimum value of the function. In each iteration, we calculate the partial derivatives of the loss function with respect to each parameter of the neural network. For those who are not very familiar with this type of calculation, let me give you a hint: derivatives can describe the slope of a function. Because of this, we can know how to manipulate the variables to move downward in the graph. To give everyone an intuitive feel for how gradient descent works, I prepared a small visualization, as shown in the figure below. You can see that as the training batches increase, we get closer to the minimum value. The same working principle applies in our neural network — the gradients calculated in each iteration show us which direction to move. The main difference is that in our neural network, we have more parameters to adjust. So how do we calculate such complex derivatives?

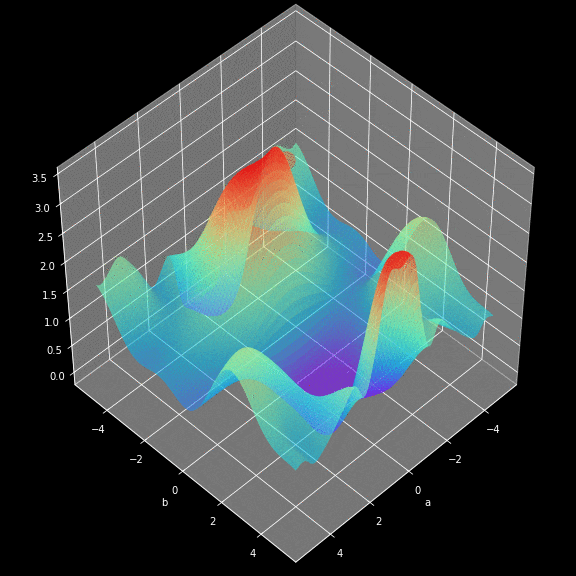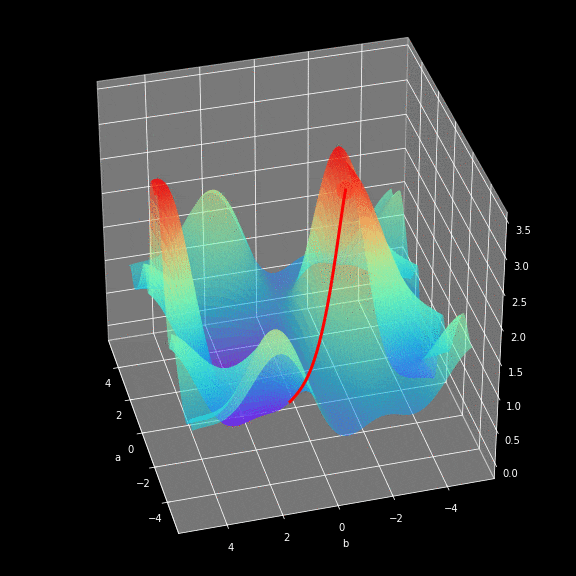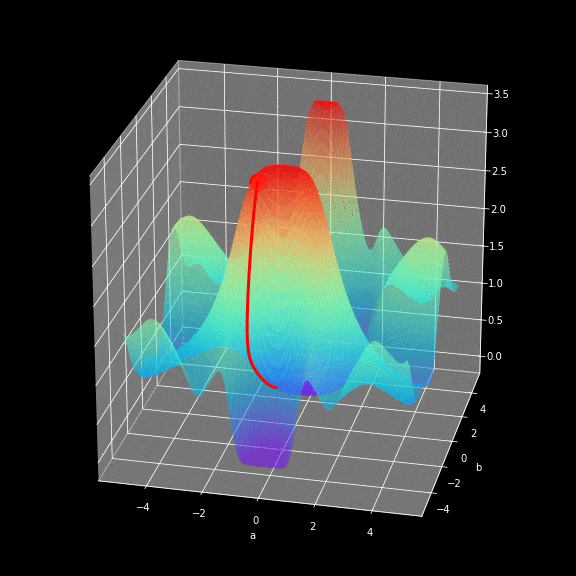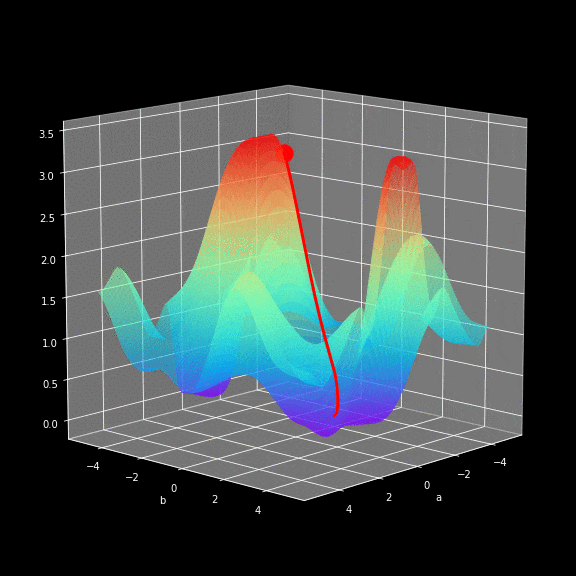
Backpropagation

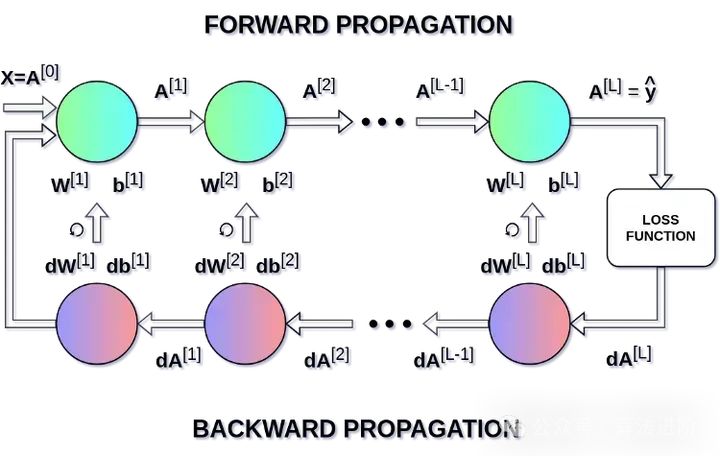
Backpropagation is an algorithm that allows us to compute very complex gradients, such as those needed in our example. The parameters of the neural network are adjusted according to the following formula.

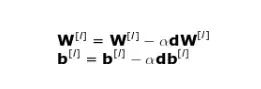
In the equation above, α represents the learning rate — this hyperparameter allows us to control the size of the adjustment. Choosing the learning rate is crucial; if it’s set too low, the neural network will learn very slowly; if it’s set too high, we won’t be able to reach the minimum loss. By using the chain rule and the partial derivatives of the loss function with respect to W and b to compute dW and db, the sizes of these two are equal to W and b, respectively. The second image below shows the order of operations in the neural network. We can clearly see how forward propagation and backpropagation work together to optimize the loss function.

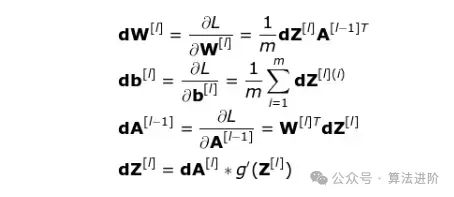
Conclusion

I hope this article can help you understand some of the mathematical principles behind neural networks; mastering the mathematical fundamentals will greatly assist you in using neural networks. Although this article lists some important content, it is only the tip of the iceberg. I strongly recommend that you try writing a small neural network using some simple frameworks without relying on very advanced frameworks; this will deepen your understanding of machine learning.

This article is reprinted from “Algorithm Advancement”.

(End)

Leave a Comment Cancel reply