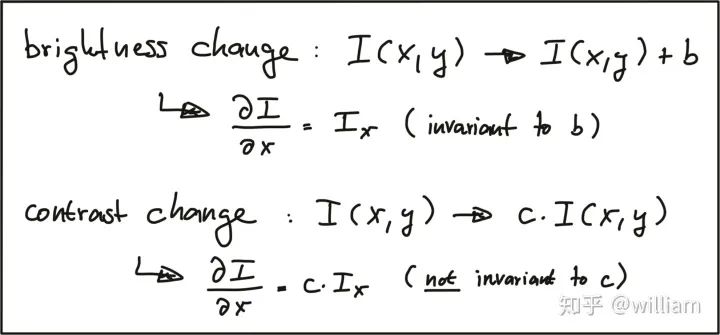Click on the above “Visual Learning for Beginners”, select “Add to Favorites” or “Pin to Top”
Essential knowledge delivered instantly Link: https://zhuanlan.zhihu.com/p/133301967
This article is for sharing only, infringement will be deleted
Link: https://zhuanlan.zhihu.com/p/133301967
This article is for sharing only, infringement will be deleted
Feature extraction and matching are crucial tasks in many computer vision applications, widely used in motion structure, image retrieval, object detection, etc. The feature detector that every computer vision beginner learns about first is almost always the HARRIS released in 1988. Over the following decades, various feature detectors/descriptors emerged, improving both the accuracy and speed of feature detection.
Feature extraction and matching consist of three steps: keypoint detection, keypoint feature description, and keypoint matching. The combinations of different detectors, descriptors, and matchers often confuse beginners. This article will mainly introduce the principles behind keypoint detection, description, and matching, the advantages and disadvantages of different combinations, and propose several optimal combinations based on practical results.
Feature Extraction and Matching
Feature
A feature is a piece of information related to solving a computational task for a specific application. Features can be specific structures in an image, such as points, edges, or objects. Features may also be the result of general neighborhood operations or feature detection applied to the image. These features can be divided into two main categories:
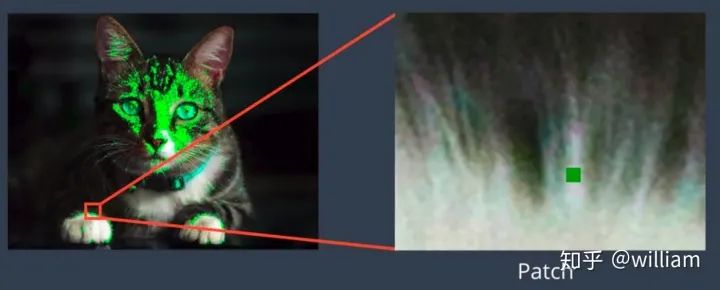
1. Features located at specific positions in the image, such as peaks, building corners, doorways, or interestingly shaped snow blocks. These localized features are often referred to as keypoint features (or even corner points), and they are usually described by pixel blocks appearing around the point position, often called image patches.
2. Features that can be matched based on their direction and local appearance (edge contours) are called edges, which can also indicate object boundaries and occlusion events in image sequences.
Main Components of Feature Extraction and Matching
1. Detection: Identifying interest points
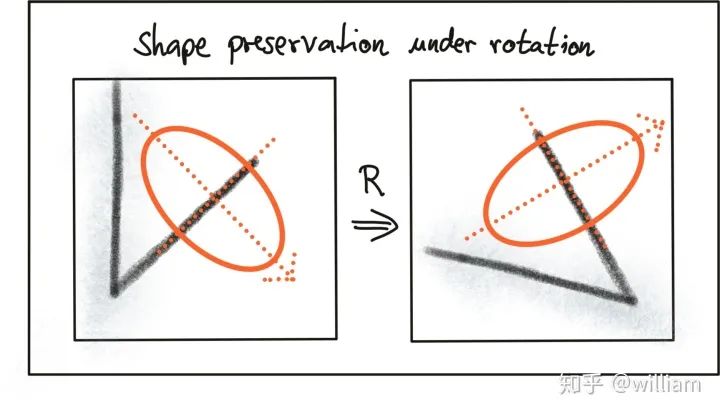
2. Description: Describing the local appearance around each feature point, this description is (ideally) invariant to changes in illumination, translation, scale, and in-plane rotation. We usually provide a descriptor vector for each feature point.
3. Matching: Identifying similar features by comparing descriptors in the images. For two images, we can obtain a set of pairs (Xi, Yi) -> (Xi’, Yi’), where (Xi, Yi) are the features of one image, and (Xi’, Yi’) are the features of another image.
Keypoints/Interest Points
Keypoints, also known as interest points, are points that express texture. Keypoints are often points where the direction of the object boundary changes suddenly or the intersection between two or more edge segments. They have a definite position in image space or are well localized. Even in the presence of disturbances such as changes in illumination and brightness in the local or global image domain, keypoints remain stable and can be reliably computed repeatedly. In addition, they should provide effective detection.
There are two methods for computing keypoints:
1. Based on image brightness (usually through image derivatives).
2. Based on boundary extraction (usually through edge detection and curvature analysis).
Invariance to Photometric and Geometric Changes in Keypoint Detectors
In the OPENCV library, we can choose from many feature detectors. The choice of feature detector depends on the type of keypoints to be detected and the properties of the image, considering the robustness of the corresponding detectors to photometric and geometric transformations.
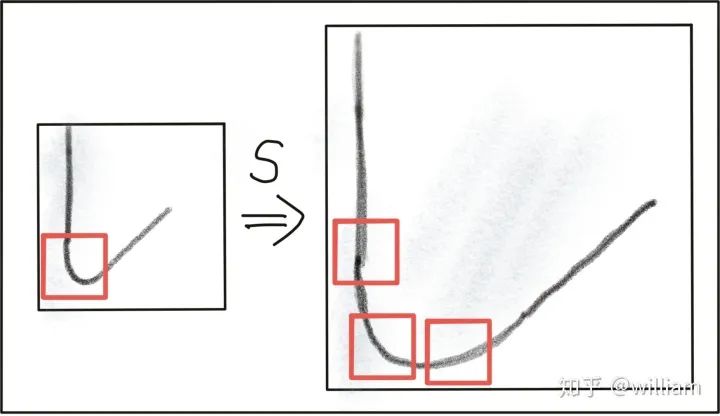
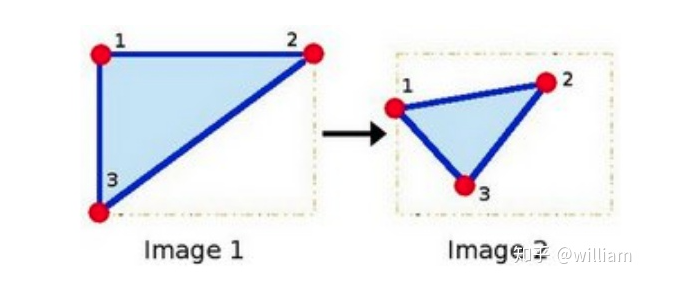
When selecting the appropriate keypoint detector, we need to consider four basic transformation types:
1. Rotation Transformation
3. Intensity Transformation
The Graffiti sequence is one of the standard image sets used in computer vision, where we can observe that the graffiti image in frame i+n includes all transformation types. For the highway sequence, when focusing on the vehicle in front, there are only scale and intensity changes between frame i and frame i + n.
The traditional HARRIS sensor is robust against rotation and additive intensity offset, but sensitive to scale changes, multiplicative intensity offset (i.e., contrast changes), and affine transformations.
Automatic Scale Selection
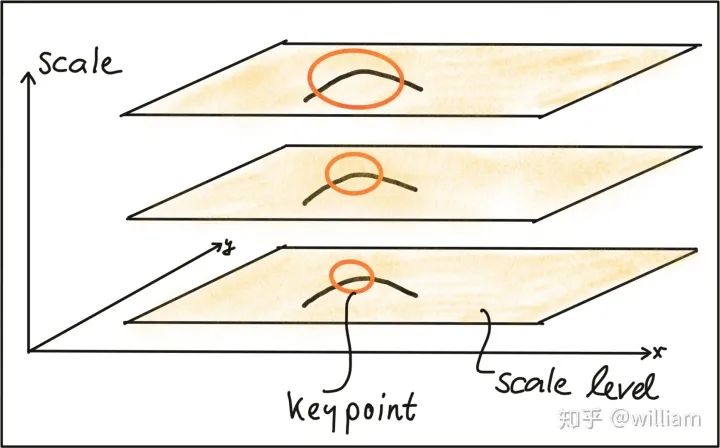
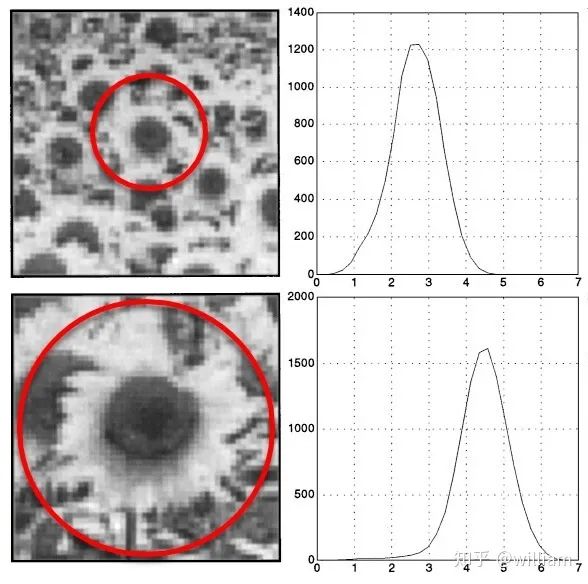
To detect keypoints at the ideal scale, we must know (or find) their respective dimensions in the image and adapt to the size of the Gaussian window w(x, y) introduced earlier in this section. If the scale of keypoints is unknown or if keypoints exist in images of different sizes, detection must be performed continuously at multiple scales.
Based on the standard deviation increment between adjacent layers, the same keypoint may be detected multiple times. This raises the issue of selecting the “correct” scale that best represents the keypoint. In 1998, Tony Lindeberg published a method for “Feature Detection with Automatic Scale Selection”. It proposed a function f(x, y, scale) that can be used to select keypoints with stable maxima at scale FF. The scale that maximizes Ff is referred to as the “feature scale” of each keypoint.
The following figure shows such a function FF, evaluated over several scale levels, with a clear maximum visible in the second image, which can be seen as the feature scale of the image content within the circular area.
A good detector can automatically select the feature scale of keypoints based on the structural characteristics of the local neighborhood. Modern keypoint detectors typically have this capability, making them robust to changes in image scale.
Common Keypoint Detectors
Keypoint detectors are a very popular research area, and many powerful algorithms have been developed over the years. Applications of keypoint detection include object recognition and tracking, image matching and panorama stitching, as well as robotic mapping and 3D modeling. The choice of detector also requires comparing the invariance in the transformations mentioned above, as well as the detection performance and processing speed of the detectors.
Classic Keypoint Detectors
The purpose of classic keypoint detectors is to maximize detection accuracy, with complexity generally not being the primary consideration.
HARRIS– 1988 Harris Corner Detector (Harris, Stephens)
Shi, Tomasi– 1996 Good Features to Track (Shi, Tomasi)
SIFT– 1999 Scale Invariant Feature Transform (Lowe) – None free
SURF– 2006 Speeded Up Robust Features (Bay, Tuytelaars, Van Gool) – None free
Modern Keypoint Detectors
In recent years, some faster detectors have been developed for real-time applications on smartphones and other portable devices. The following list shows the most popular detectors belonging to this group:
FAST– 2006 Features from Accelerated Segment Test (FAST) (Rosten, Drummond)
BRIEF– 2010 Binary Robust Independent Elementary Features (BRIEF) (Calonder, et al.)
ORB– 2011 Oriented FAST and Rotated BRIEF (ORB) (Rublee et al.)
BRISK– 2011 Binary Robust Invariant Scalable Keypoints (BRISK) (Leutenegger, Chli, Siegwart)
FREAK– 2012 Fast Retina Keypoint (FREAK) (Alahi, Ortiz, Vandergheynst)
KAZE– 2012 KAZE (Alcantarilla, Bartoli, Davidson)
Gradient and Binary Based Descriptors
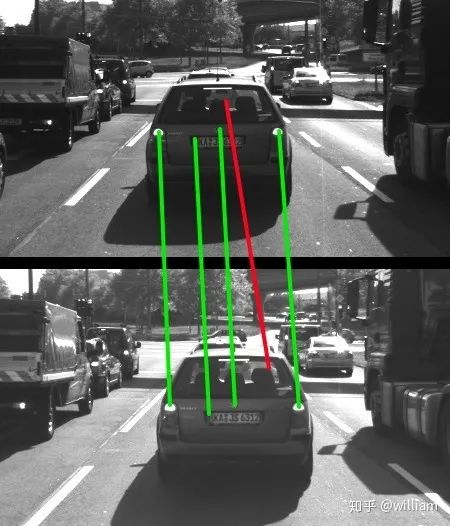
Since our task is to find corresponding keypoints in image sequences, we need a method based on similarity measures to reliably assign keypoints to each other. Various similarity measures (called Descriptors) have been proposed in the literature, and many authors have simultaneously published a new method for keypoint detection along with optimized similarity measures for their keypoint types. In other words, most of the wrapped OPENCV keypoint detector functions can also be used to generate keypoint descriptors.
Keypoint detectors are algorithms that select points from images based on the local maxima of a function, such as the “corner” metric we see in the HARRIS detector.
Keypoint descriptors are vectors used to describe the pixel values of the image patches around keypoints. The description methods range from simple pixel value comparisons to more complex methods, such as histograms of gradient directions.
Keypoint detectors generally find feature points from a frame image. Descriptors help us in the “keypoint matching” step to assign similar keypoints in different images to each other. As shown in the figure below, a set of keypoints in one frame is assigned to keypoints in another frame to maximize the similarity of their respective descriptors, and these keypoints represent the same object in the image. Besides maximizing similarity, good descriptors should also minimize mismatches, i.e., avoid assigning keypoints that do not correspond to the same object to each other.
HOG Based Descriptors
Despite the emergence of faster detectors/descriptor combinations, the Scale Invariant Feature Transform (SIFT), one of the histogram of oriented gradients (HOG) based descriptors, is still widely used. The basic idea of HOG is to describe the structure of an object through the distribution of intensity gradients in the local neighborhood of the object. To do this, the image is divided into multiple cells, where gradients are computed and collected into histograms. Then, the histogram sets of all cells are used as similarity measures to uniquely identify image blocks or objects.
SIFT/SURF uses HOG as a descriptor, including both keypoint detectors and descriptors, and is very powerful, but is patent protected. SURF is an improvement on SIFT, which not only increases computational speed but also enhances robustness; the implementation principles of both are quite similar. Here I will only introduce SIFT.
The SIFT method follows a five-step process, which will be briefly summarized below.
First, a method called “Laplacian of Gaussian (LoG)” is used to detect keypoints in the image, which is based on the second-order intensity derivative. LoG is applied at various scale levels of the image and tends to detect blobs rather than corners. In addition to using a unique scale level, directions are assigned to keypoints based on the intensity gradients in the local neighborhood around the keypoints.
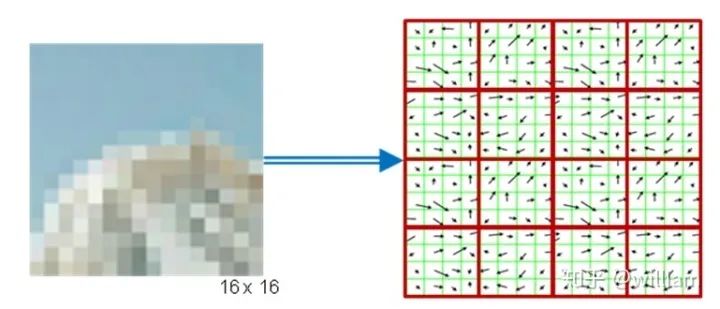
Second, the surrounding area of each keypoint is changed by eliminating directions, ensuring a normalized direction. Moreover, the size of this area is adjusted to 16 x 16 pixels, providing a standardized image patch.
Third, the direction and magnitude of each pixel in the normalized image patch are calculated based on intensity gradients _Ix_ and _Iy_.
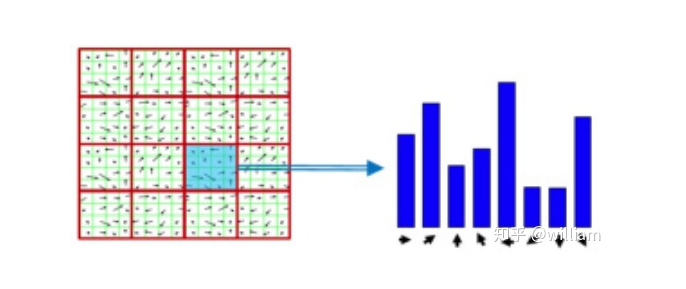
Fourth, the normalized patch is divided into a grid of 4 x 4 cells. Within each cell, the directions of pixels exceeding the magnitude threshold are collected in a histogram consisting of 8 bins.
Finally, all 16 cell histograms of 8 bins are concatenated into a 128-dimensional vector (descriptor), which uniquely represents the keypoint.
The SIFT detector/descriptor can reliably identify objects even in clutter and partial occlusion. Uniform changes in scale, rotation, brightness, and contrast are invariant, and affine distortions are even invariant.
The disadvantage of SIFT is its low speed, which makes it unsuitable for real-time applications like smartphones. Other members of the HOG series (such as SURF and GLOH) have been optimized for speed. However, they are still computationally expensive and should not be used in real-time applications. Moreover, SIFT and SURF are heavily patented, so they cannot be freely used in commercial environments. To use SIFT in OpenCV, you must include#include <opencv2/xfeatures2d/nonfree.hpp>and install the OPENCV_contribute package, ensuring to enableOPENCV_ENABLE_NONFREEin the Cmake options.
The problem with HOG-based descriptors is that they rely on computing intensity gradients, which is a very expensive operation. While some improvements have been made (e.g., SURF), using integral images has increased speed, but these methods are still unsuitable for real-time applications on devices with limited processing power (e.g., smartphones). The binary descriptor family is a faster (free) alternative to HOG-based methods, but with slightly lower accuracy and performance.
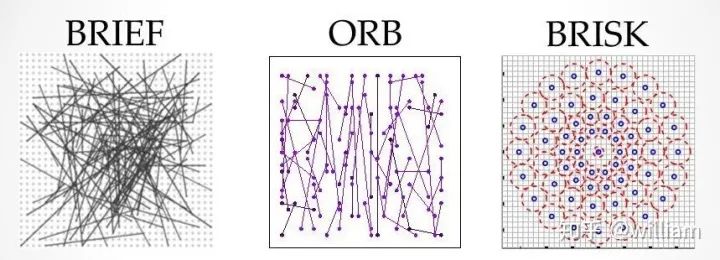
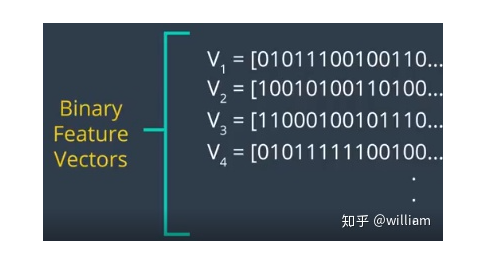
The core idea of binary descriptors is to rely solely on intensity information (i.e., the image itself) and encode information around keypoints into a string of binary numbers, which can be compared very efficiently during the matching step. In other words, binary descriptors encode the information of interest points into a series of numbers, serving as a digital “fingerprint” that can differentiate one feature from another. Currently, the most popular binary descriptors are BRIEF, BRISK, ORB, FREAK, and KAZE (all of which can be found in the OpenCV library).
From a high-level perspective, binary descriptors consist of three main components:
1. A sampling pattern that describes the location of sample points around the keypoint.
2. A direction compensation method that eliminates the influence of rotation around the keypoint position on the image patch.
3. A sample pair selection method that generates paired sample points, which are compared based on their intensity values. If the first value is greater than the second value, we write a “1” in the binary string; otherwise, we write a “0”. After performing this on all pairs of points in the sampling pattern, a long binary chain (or “string”) is created (hence the name of the descriptor class family).
BRISK “Binary Robust Invariant Scalable Keypoints” keypoint detector/descriptor is representative of binary descriptors. Here I will only introduce BRISK.
Proposed by Stefan Leutenegger in 2011, BRISK is a combination of a FAST detector and a Binary Descriptor, created by specifically sampling the intensity comparisons around each keypoint neighborhood.
The sampling pattern of BRISK consists of multiple sampling points (in blue), with concentric rings (in red) around each sampling point representing the area where Gaussian smoothing is applied. Unlike some other binary descriptors (such as ORB or Brief), BRISK’s sampling pattern is fixed. Smoothing is crucial to avoid aliasing (this effect causes different signals to become difficult to distinguish when sampled or to interfere with each other).
During the sample pair selection, the BRISK algorithm distinguishes between long-distance pairs and short-distance pairs. Long-distance pairs (i.e., sample points that have minimal distance from each other in the sampling pattern) are used to estimate the direction of the image patch based on intensity gradients, while short-distance pairs are used for intensity comparisons of the assembled descriptor string. Mathematically, these pairs are represented as follows:
First, we define the set of all possible sampling point pairs A. Then, we extract a subset L from A, where the Euclidean distance of subset L is greater than the upper threshold. L is used for long-distance pairs for direction estimation. Finally, we extract those pairs from A where the Euclidean distance is below the lower threshold. This set S contains short-distance pairs used to assemble the binary descriptor string.
The following figure shows the two types of distance pairs on the sampling pattern: short pairs (left) and long pairs (right).
From the long pairs, the keypoint direction vector G is calculated as follows:
First, the gradient intensity between two sampled points is computed based on normalized unit vectors, which provide the direction between the two points multiplied by the intensity difference at each point. Then, in (2), the keypoint direction vector g is calculated from the total sum of all gradient intensities.
Based on g, we can rearrange the short-distance pairs using the direction of the sampling pattern to ensure rotational invariance. Using the rotation-invariant short-distance pairs, the final binary descriptor can be constructed as follows:
Once the orientation vector of the keypoint is calculated from g, we use it to make the short-distance pairs rotation-invariant. Then, the intensities S between all pairs are compared and used to assemble a binary descriptor that can be used for matching.
OPENCV Detector/Descriptor Implementation
Currently, there are various feature point detectors/descriptors, such as HARRIS, SHI-TOMASI, FAST, BRISK, ORB, AKAZE, SIFT, FREAK, BRIEF. Each of these deserves a separate blog post for description, but the purpose of this article is to provide an overview, so I will not analyze these detectors/descriptors in detail from a theoretical perspective. There are many articles online describing these detectors/descriptors, but I still recommend that you first look at the OPENCV library’s Tutorial: How to Detect and Track Objects With OpenCV.
Below, I will introduce the code implementation and parameter details of each feature point detector/descriptor, and at the end of the article, evaluate these combinations based on practical results.
Some OPENCV functions can be used for both detectors/descriptors, but some combinations may have issues.
SIFT Detector/Descriptor SIFT detector and ORB descriptor do not work together
int nfeatures = 0; // The number of best features to retain.int nOctaveLayers = 3; // The number of layers in each octave. 3 is the value used in D. Lowe paper.double contrastThreshold = 0.04; // The contrast threshold used to filter out weak features in semi-uniform (low-contrast) regions. double edgeThreshold = 10; // The threshold used to filter out edge-like features. double sigma = 1.6; // The sigma of the Gaussian applied to the input image at the octave #0.xxx=cv::xfeatures2d::SIFT::create(nfeatures, nOctaveLayers, contrastThreshold, edgeThreshold, sigma);
// Detector parametersint blockSize = 2; // for every pixel, a blockSize × blockSize neighborhood is consideredint apertureSize = 3; // aperture parameter for Sobel operator (must be odd)int minResponse = 100; // minimum value for a corner in the 8bit scaled response matrixdouble k = 0.04; // Harris parameter (see equation for details)// Detect Harris corners and normalize outputcv::Mat dst, dst_norm, dst_norm_scaled;dst = cv::Mat::zeros(img.size(), CV_32FC1);cv::cornerHarris(img, dst, blockSize, apertureSize, k, cv::BORDER_DEFAULT);cv::normalize(dst, dst_norm, 0, 255, cv::NORM_MINMAX, CV_32FC1, cv::Mat());cv::convertScaleAbs(dst_norm, dst_norm_scaled);// Look for prominent corners and instantiate keypointsdouble maxOverlap = 0.0; // max. permissible overlap between two features in %, used during non-maxima suppressionfor (size_t j = 0; j < dst_norm.rows; j++) { for (size_t i = 0; i < dst_norm.cols; i++) { int response = (int) dst_norm.at<float>(j, i); if (response > minResponse) { // only store points above a threshold cv::KeyPoint newKeyPoint; newKeyPoint.pt = cv::Point2f(i, j); newKeyPoint.size = 2 * apertureSize; newKeyPoint.response = response; // perform non-maximum suppression (NMS) in local neighbourhood around new key point bool bOverlap = false; for (auto it = keypoints.begin(); it != keypoints.end(); ++it) { double kptOverlap = cv::KeyPoint::overlap(newKeyPoint, *it); if (kptOverlap > maxOverlap) { bOverlap = true; if (newKeyPoint.response > (*it).response) { // if overlap is >t AND response is higher for new kpt *it = newKeyPoint; // replace old key point with new one break; // quit loop over keypoints } } } if (!bOverlap) { // only add new key point if no overlap has been found in previous NMS keypoints.push_back(newKeyPoint); // store new keypoint in dynamic list } } } // eof loop over cols} // eof loop over rows
int blockSize = 6; // size of an average block for computing a derivative covariation matrix over each pixel neighborhooddouble maxOverlap = 0.0; // max. permissible overlap between two features in %double minDistance = (1.0 - maxOverlap) * blockSize;int maxCorners = img.rows * img.cols / max(1.0, minDistance); // max. num. of keypointsdouble qualityLevel = 0.01; // minimal accepted quality of image cornersdouble k = 0.04;bool useHarris = false;// Apply corner detectionvector<cv::Point2f> corners;cv::goodFeaturesToTrack(img, corners, maxCorners, qualityLevel, minDistance, cv::Mat(), blockSize, useHarris, k);// add corners to result vectorfor (auto it = corners.begin(); it != corners.end(); ++it) { cv::KeyPoint newKeyPoint; newKeyPoint.pt = cv::Point2f((*it).x, (*it).y); newKeyPoint.size = blockSize; keypoints.push_back(newKeyPoint);}
BRISK Detector/Descriptor
int threshold = 30; // FAST/AGAST detection threshold score.int octaves = 3; // detection octaves (use 0 to do single scale)float patternScale = 1.0f; // apply this scale to the pattern used for sampling the neighbourhood of a keypoint.xxx=cv::BRISK::create(threshold, octaves, patternScale);
FREAK Detector/Descriptor
bool orientationNormalized = true;// Enable orientation normalization.bool scaleNormalized = true;// Enable scale normalization.float patternScale = 22.0f;// Scaling of the description pattern.int nOctaves = 4;// Number of octaves covered by the detected keypoints.const std::vector<int> &selectedPairs = std::vector<int>(); // (Optional) user defined selected pairs indexes,xxx=cv::xfeatures2d::FREAK::create(orientationNormalized, scaleNormalized, patternScale, nOctaves,selectedPairs);
int threshold = 30;// Difference between intensity of the central pixel and pixels of a circle around this pixelbool nonmaxSuppression = true;// perform non-maxima suppression on keypoints cv::FastFeatureDetector::DetectorType type = cv::FastFeatureDetector::TYPE_9_16;// TYPE_9_16, TYPE_7_12, TYPE_5_8xxx=cv::FastFeatureDetector::create(threshold, nonmaxSuppression, type);
ORB Detector/Descriptor SIFT detector and ORB descriptor do not work together
int nfeatures = 500;// The maximum number of features to retain.float scaleFactor = 1.2f;// Pyramid decimation ratio, greater than 1.int nlevels = 8;// The number of pyramid levels.int edgeThreshold = 31;// This is size of the border where the features are not detected.int firstLevel = 0;// The level of pyramid to put source image to.int WTA_K = 2;// The number of points that produce each element of the oriented BRIEF descriptor.auto scoreType = cv::ORB::HARRIS_SCORE;// The default HARRIS_SCORE means that Harris algorithm is used to rank features.int patchSize = 31;// Size of the patch used by the oriented BRIEF descriptor.int fastThreshold = 20;// The fast threshold.xxx=cv::ORB::create(nfeatures, scaleFactor, nlevels, edgeThreshold, firstLevel, WTA_K, scoreType,patchSize, fastThreshold);
AKAZE Detector/Descriptor KAZE/AKAZE descriptors will only work with KAZE/AKAZE detectors.
auto descriptor_type = cv::AKAZE::DESCRIPTOR_MLDB;// Type of the extracted descriptor: DESCRIPTOR_KAZE, DESCRIPTOR_KAZE_UPRIGHT, DESCRIPTOR_MLDB or DESCRIPTOR_MLDB_UPRIGHT.int descriptor_size = 0;// Size of the descriptor in bits. 0 -> Full sizeint descriptor_channels = 3;// Number of channels in the descriptor (1, 2, 3)float threshold = 0.001f;// Detector response threshold to accept pointint nOctaves = 4;// Maximum octave evolution of the imageint nOctaveLayers = 4;// Default number of sublevels per scale levelauto diffusivity = cv::KAZE::DIFF_PM_G2;// Diffusivity type. DIFF_PM_G1, DIFF_PM_G2, DIFF_WEICKERT or DIFF_CHARBONNIERxxx=cv::AKAZE::create(descriptor_type, descriptor_size, descriptor_channels, threshold, nOctaves,nOctaveLayers, diffusivity);
BRIEF Detector/Descriptor
int bytes = 32;// Length of the descriptor in bytes, valid values are: 16, 32 (default) or 64 .bool use_orientation = false;// Sample patterns using keypoints orientation, disabled by default.xxx=cv::xfeatures2d::BriefDescriptorExtractor::create(bytes, use_orientation);
Feature matching, or image matching in general, is part of computer vision applications such as image registration, camera calibration, and object recognition; it is the task of establishing correspondences between two images of the same scene/target. A common image matching method detects a set of interest points associated with image descriptors from image data. Once features and descriptors are extracted from two or more images, the next step is to establish some preliminary feature matches between these images.
In general, the performance of feature matching methods depends on the nature of the underlying keypoints and the choice of associated image descriptors.
We have learned that keypoints can be described by transforming their local neighborhoods into high-dimensional vectors, which can capture unique characteristics of gradient or intensity distributions.
Distance Between Descriptors
Feature matching requires calculating the distance between two descriptors, allowing their differences to be converted into a single number, which we can use as a simple similarity measure.
Currently, there are three distance metrics:
-
Sum of Absolute Differences (SAD) – L1-norm
-
Sum of Squared Differences (SSD) – L2-norm
-
The difference between SAD and SSD is that: first, the shortest distance between the two is a straight line, given the two components of each vector; SAD computes the sum of length differences, which is a one-dimensional process. SSD computes the sum of squares, following the Pythagorean theorem, where the total of the squares of the longer sides equals the square of the hypotenuse in a right triangle. Therefore, in terms of geometric distance between the two vectors, L2-norm is a more accurate measure. Note that the same principle applies to high-dimensional descriptors.
Hamming distance is very suitable for binary descriptors composed only of 1s and 0s, calculated by using the XOR function to compute the differences between two vectors; if two bits are the same, it returns zero; if the two bits differ, it returns one. Therefore, the total of all XOR operations is the number of different bits between the two descriptors.
It is worth noting that a suitable distance metric must be chosen based on the type of descriptor used.
-
BINARY descriptors: BRISK, BRIEF, ORB, FREAK, and AKAZE – Hamming Distance
-
HOG descriptors: SIFT (and SURF and GLOH, all patented) – L2-norm
Finding Matching Pairs
Let’s assume there are N keypoints and their associated descriptors in one image, and M keypoints in another image.
Brute Force Matching
The most obvious way to find corresponding pairs is to compare all features with each other, i.e., performing N x M comparisons. For each keypoint in the first image, it will take every keypoint in the second image and calculate the distance. The keypoint with the smallest distance will be considered a pair. This method is called “Brute Force Matching” or “Nearest Neighbor Matching”. The output of brute force matching in OPENCV is a list of keypoint pairs, sorted by the distance of their descriptors under the selected distance function.
Fast Nearest Neighbor (FLANN)
In 2014, David Lowe and Marius Muja released