Reading articles about LLMs, you often see phrases like “we use the standard Transformer architecture.” But what does “standard” mean, and has it changed since the original paper?
Interestingly, despite the rapid growth in the NLP field over the past five years, the Vanilla Transformer still adheres to the Lindy Effect, which suggests that the longer something exists, the longer it is likely to continue existing in the future.
“The Lindy Effect is a concept originating from a deli in New York City, referring to the idea that the future life expectancy of a non-perishable item (such as a technology, idea, or cultural phenomenon) is proportional to its current age. In short, the longer something has existed, the longer it is likely to continue existing.
This concept has become popular in discussions about technology, books, ideas, and even social structures. For example, a book that has been published for 100 years may remain a bestseller for another 100 years, while a newly published book may not have such a long future. “
Below are the five major changes summarized from the image:
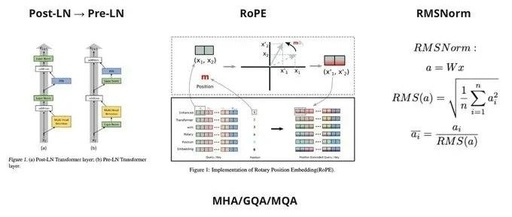
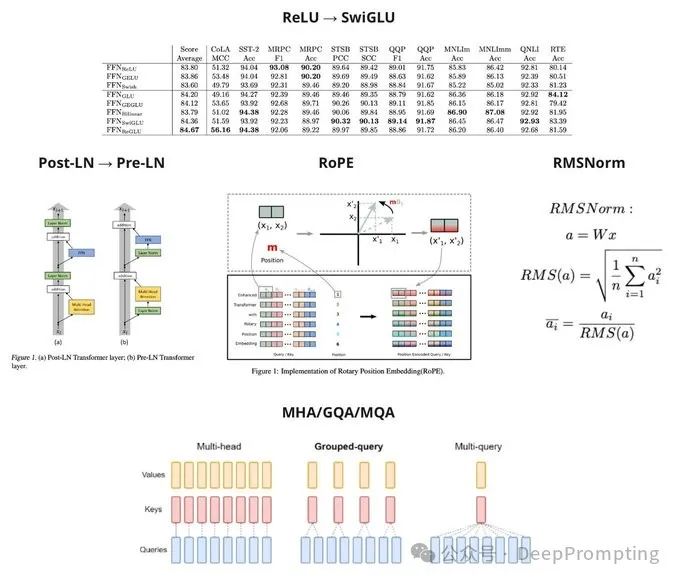
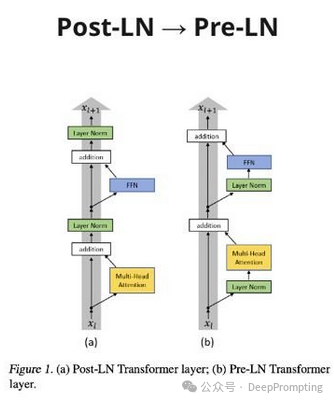
(1) Using the language model (i.e., decoder-only) LLaMa-2 as an example, let’s look at the main architectural improvements of LLMs: — Post LayerNorm → Pre LayerNorm (https://arxiv.org/abs/2002.04745). This makes convergence more stable. Now, the process involves the original embeddings simply passing through the decoder blocks, with the adjustments from FFN and Attention added in the Residual Connection way.
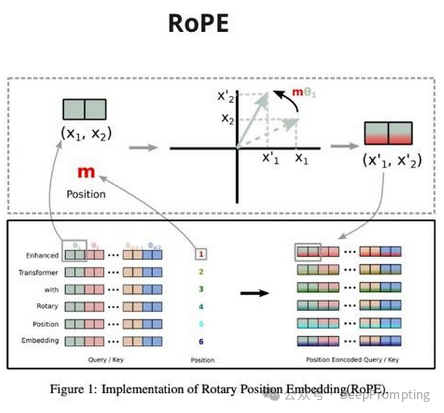
(2) — Absolute Position Embedding → RoPE (https://arxiv.org/abs/2104.09864). This method rotates token embeddings by a certain angle based on their position. Moreover, it performs very well. Additionally, this method has undergone many modifications to extend context to very large numbers.
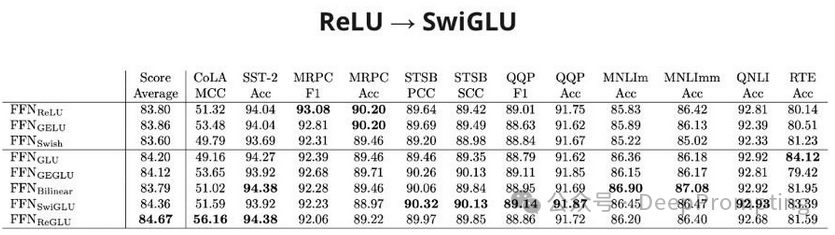
(3) — ReLU Activation → SwiGLU (https://arxiv.org/abs/2002.05202). The gated linear unit (part of the SwiGLU series of methods) adds an operation of element-wise multiplication of matrices, where one matrix has been passed through a sigmoid, thus controlling the signal strength passed from the first matrix, which slightly improves the quality of multi-tasking.
(4) LayerNorm → RMSNorm (https://arxiv.org/abs/1910.07467). RMSNorm is computationally simpler but maintains the same quality.
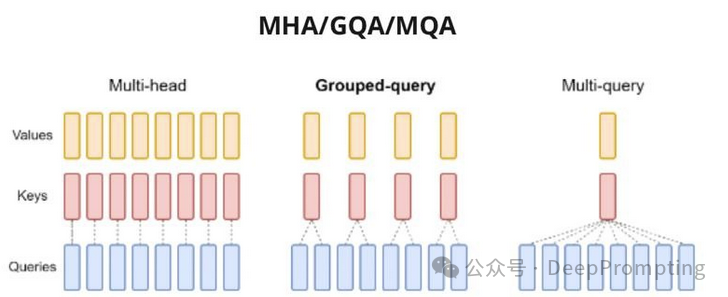
(5) Attention Modifications (https://arxiv.org/abs/2305.13245), for example, using one pair of K-V matrices for each group of Q matrices at a time. This improvement has primarily affected optimization during inference. However, there are also many methods aimed at reducing computational quadratic complexity.
