This article is about 9300 words, recommended reading 10+ minutes.
This article will explore the interpretability of the attention mechanism.
Introduction
Since Bahdanau introduced Attention as soft alignment in neural machine translation in 2014, a large number of natural language processing works have regarded it as an important module for improving model performance. Numerous experiments have shown that the Attention mechanism is computationally efficient and effective. Consequently, discussions on its interpretability have emerged. On one hand, people hope to better understand its internal mechanisms to optimize models; on the other hand, some scholars have raised doubts about it. Here, as a prospective PhD student at SCIR laboratory, I have written this reflective note on related papers based on my understanding of the Attention mechanism, hoping to inspire readers. Due to my personal limitations, any errors in the text are welcome to be pointed out by everyone.
1. Attention Mechanism
1.1 Background
The Attention mechanism is currently one of the most commonly used methods in the field of natural language processing, as it can significantly improve model performance on a series of tasks, especially in sequence-to-sequence models based on recurrent neural networks. Coupled with the extensive use of the Transformer model proposed by Google, which is entirely based on Attention, and the BERT model, the Attention mechanism is practically a textbook technology. On one hand, Attention intuitively simulates the human behavior of focusing on certain keywords when understanding language, just as Bahdanau introduced it as soft alignment in neural machine translation. On the other hand, numerous experiments over the years have shown that Attention is indeed a feasible and efficient method for enhancing model performance. Therefore, further exploring the intrinsic principles of this mechanism, explaining its effectiveness, and providing evidence is a valuable research direction.
1.2 Structure
After a long period of development, although the implementation methods in different papers may vary, they generally follow the same paradigm, which includes three components:
-
Key corresponds to the value and is used to compute similarity with the query as the basis for selecting Attention;
-
Query is the query during one execution of Attention;
-
Value is the data that is attended to and selected.
The corresponding formula is:
Where the value Value is often the output of the previous layer and generally remains unchanged, while other parts such as key, query, and the similarity function often have different implementation methods. Here we will first introduce the Attention structure implemented by Bahdanau and Yang, as it serves as the basis for the subsequent interpretability explorations by Serrano and Jain.
The formula for Attention is as follows:
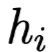 (As Value) is the output tensor at the i-th position in the sequence from the previous layer. If the previous layer is a bidirectional RNN structure, then
(As Value) is the output tensor at the i-th position in the sequence from the previous layer. If the previous layer is a bidirectional RNN structure, then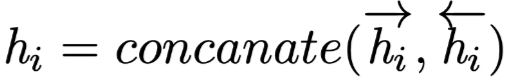 ;
;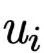 is the key Key at the i-th position, calculated from the value Value through a fully connected layer;
is the key Key at the i-th position, calculated from the value Value through a fully connected layer;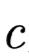 is the query Query of this Attention layer, initialized randomly and updated synchronously during training. If Attention is not a standalone layer but is built on the decoder, then
is the query Query of this Attention layer, initialized randomly and updated synchronously during training. If Attention is not a standalone layer but is built on the decoder, then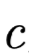 is related to the output at the corresponding position during the encoding phase; the similarity function is matrix dot product, and the resulting
is related to the output at the corresponding position during the encoding phase; the similarity function is matrix dot product, and the resulting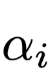 is the Attention weight,
is the Attention weight,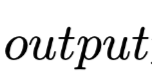 is the output of the Attention layer.
The core idea is as follows:
is the output of the Attention layer.
The core idea is as follows:
-
Calculate a non-negative normalized weight for each input element;
-
Multiply these weights by the corresponding component representations;
-
Sum the results to produce a fixed-length representation.
This is the original form of Attention, and the experimental tests on its interpretability are also based on this model.
2. Definition of Interpretability
There are various definitions of interpretability, and most related articles often derive differences from here, leading to different conclusions. However, there is some consensus that can be summarized.
The conceptual consensus on interpretability can be described as follows: if a model is interpretable, humans can understand this model, which can be divided into two aspects. One is that the model is transparent to humans, meaning that corresponding parameters and model decisions can be predicted before training on specific tasks. The second is that after a model makes a decision, humans can understand the reasons behind that decision. There are also other definitions from different perspectives, for example: interpretability means that one can reconstruct the model’s decision-making process artificially.
Specifically, for the interpretability of the Attention model, it can generally be refined to:
-
The height of Attention weights should be positively correlated with the importance of the corresponding positional information;
-
Input units with high weights have a decisive effect on the output results.
3. Specific Arguments
3.1 Not Explanation
Regarding non-interpretability, Serrano and Jain each proposed some experiments and arguments. Their works overlap and complement each other. The former’s work explores a relatively shallow level, only considering whether the weights of the Attention layer are positively correlated with the corresponding input positions. The method used is intermediate representation erasure, i.e., continuously nullifying some weights to observe changes in the model. The article mainly explores different erasure methods, while the latter’s work is slightly deeper, exploring not only the impact of removing key weights on the model but also introducing the idea of constructing adversarial Attention weights to test changes in the model.
3.1.1 Intermediate Representation Erasure
Intermediate representation erasure considers a relatively shallow understanding of Attention, mainly based on the logic that the more important the weight, the greater its influence on the output result, and setting it to zero will have a direct impact on the result.
First, introduce evaluation metrics, that is, how much the weights and output results change:
-
Total Variance Distance (TVD) as a metric for distinguishing output result distributions, defined as:
Where
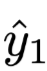 and
and 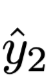 are two different output result distributions.
are two different output result distributions.
-
Jensen-Shannon Divergence (JSD) as a metric for distinguishing output result distributions and Attention weights, defined as:
Where
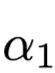 and
and 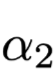 are two different distributions, which can be either output results or Attention weights,
is Kullback-Leibler Divergence.
are two different distributions, which can be either output results or Attention weights,
is Kullback-Leibler Divergence.
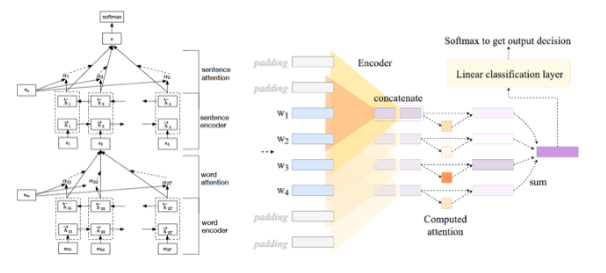
The specific implementation is shown in Figure 1. The model is divided into two parts, the first part is embedding and encoding part, for example, a fully connected layer to implement word embedding followed by a bidirectional LSTM layer for encoding. The specific models used in the experiment vary. The second part is the decoding part, which decodes the output tensor obtained from the Attention layer into the results needed for the specific task, which in the text classification task is a dimensional transformation implemented by a fully connected layer. It is important to note that here the Attention layer does not act on the decoder like in seq-to-seq models, but is tested as an independent layer.
Figure 1 Overall model of intermediate representation erasure
The entire model runs twice, the first time with normal input and output, retaining the results obtained, and the second time setting the selected erased weights on the Attention layer to 0, renormalizing the weights with Softmax, and continuing the subsequent process to obtain results, calculating the TVD metric with the data obtained from the first time. Erasing on the Attention layer rather than the input side is to isolate its impact from the preceding encoding part. Additionally, the purpose of renormalizing is that when the model sets some high-weight parameters to zero, it causes the output tensor of the Attention layer to approach zero, which is a situation the model has not encountered during training, thus leading to uncontrollable decision-making behavior of the model.
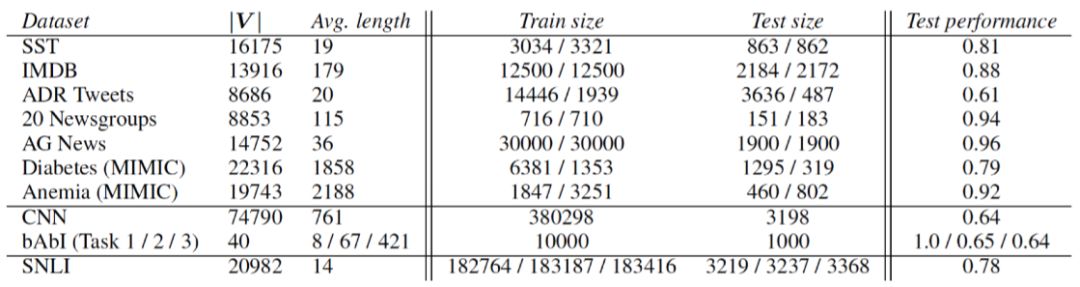
Serrano designed the experiment using a text classification task, employing four datasets as shown in Figure 2, and also designed four models for comparative testing:
Figure 2 Four text classification datasets
-
Hierarchical Attention Network proposed by Yang, a hierarchical Attention model, as shown on the left side of Figure 3, divided into word-level and sentence-level parts. The experiment only tests the sentence-level Attention layer, and the previous parts are regarded as the encoding phase;
-
Flat Attention Network modified from the previous model, which only has a word-level Attention layer operating on the entire document without sentence segmentation;
-
Flat Attention Network with CNN replacing the bidirectional RNN structure used as the encoder in the previous model with CNN, as shown on the right side of Figure 3, referencing Kim’s implementation;
-
No Encoder does not use an encoder, directly inputting the results after word embedding into the Attention layer. This control group aims to eliminate the encoder to prevent a single token from obtaining contextual information.
Figure 3 Structures of Hierarchical Attention Networks using BiRNN and CNN as the encoding parts
The experiments have two main modules, single weight zeroing and a group of weights zeroing. The difference is that the former tests the change in the entire model output after erasing the highest-weight corresponding intermediate representation, while the latter tests how many intermediate representations need to be erased and how to erase them to change the model’s final decision, thus finding evidence for interpretability from the experimental data.
Single Attention Weight’s Importance First, the highest Attention weight’s intermediate representation is erased, and the process shown in Figure 1 is used to calculate the normal result and the result after erasure for the JSD metric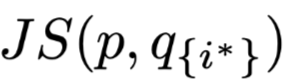 , where
, where is the distribution of the normal result,
is the distribution of the normal result,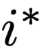 is the result distribution after erasing the highest weight’s corresponding intermediate representation. To verify how much this distance is, a random position is selected
is the result distribution after erasing the highest weight’s corresponding intermediate representation. To verify how much this distance is, a random position is selected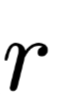 , and using the same process to erase the intermediate representation, the corresponding JSD metric is obtained
, and using the same process to erase the intermediate representation, the corresponding JSD metric is obtained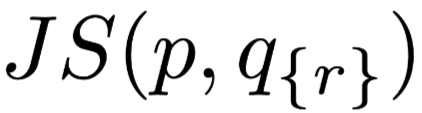 . Intuitively, if the items with high weights are indeed more important, then this formula should always be positive, and the difference in the two weights set to zero
. Intuitively, if the items with high weights are indeed more important, then this formula should always be positive, and the difference in the two weights set to zero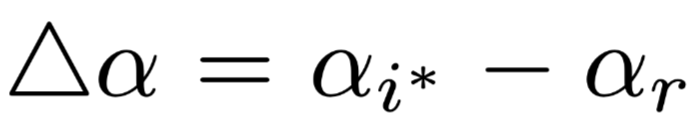 should be larger, and the value of
should be larger, and the value of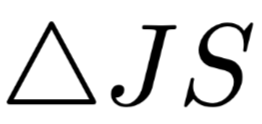 should be larger as well. The charts presented by the author in the text are shown in Figure 4 on the left, where the x-axis is the difference between the two weights, and the y-axis is the value of
should be larger as well. The charts presented by the author in the text are shown in Figure 4 on the left, where the x-axis is the difference between the two weights, and the y-axis is the value of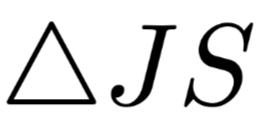 . The author states that there are almost no negative results in the data obtained, and even if there are, they are close to 0. Moreover, as the difference between the two weights increases, the degree of change in the model’s output result distribution also increases accordingly. However, the author believes that “even if the difference between the two weights reaches 0.4 (where the weights satisfy the sum normalization), most positive
. The author states that there are almost no negative results in the data obtained, and even if there are, they are close to 0. Moreover, as the difference between the two weights increases, the degree of change in the model’s output result distribution also increases accordingly. However, the author believes that “even if the difference between the two weights reaches 0.4 (where the weights satisfy the sum normalization), most positive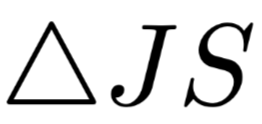 values are still very close to 0,” thus preliminarily believing that the Attention mechanism has phenomena that contradict intuition.
However, results from the appendix show that for the non-hierarchical model without an encoder, the degree of change is not as severe as claimed, meaning that under this data group, the author’s conclusion is not rigorous. The text proposes a hypothesis that when the encoding layer encodes each position’s token, it contains contextual information, suggesting that the amount of information has undergone a similar averaging operation, and the output tokens from the encoding layer contain some necessary attention information, which weakens the influence of the Attention layer’s weights. Of course, the article does not conduct experiments to verify this hypothesis.
Figure 4 Comparison of results based on the hierarchical model using BiRNN and the non-hierarchical model without an encoder
Afterwards, Serrano designed a set of experiments to strengthen the exploration of the impact of single erasure operations, using the evaluation metric of the probability of model decision flipping, that is, erasing the highest weight’s corresponding position
values are still very close to 0,” thus preliminarily believing that the Attention mechanism has phenomena that contradict intuition.
However, results from the appendix show that for the non-hierarchical model without an encoder, the degree of change is not as severe as claimed, meaning that under this data group, the author’s conclusion is not rigorous. The text proposes a hypothesis that when the encoding layer encodes each position’s token, it contains contextual information, suggesting that the amount of information has undergone a similar averaging operation, and the output tokens from the encoding layer contain some necessary attention information, which weakens the influence of the Attention layer’s weights. Of course, the article does not conduct experiments to verify this hypothesis.
Figure 4 Comparison of results based on the hierarchical model using BiRNN and the non-hierarchical model without an encoder
Afterwards, Serrano designed a set of experiments to strengthen the exploration of the impact of single erasure operations, using the evaluation metric of the probability of model decision flipping, that is, erasing the highest weight’s corresponding position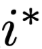 and randomly selected positions
and randomly selected positions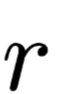 after erasing the intermediate representations, and observing the changes in model decision behavior. The experimental data is shown in Figure 5, where the orange area is where r leads to a flip and
after erasing the intermediate representations, and observing the changes in model decision behavior. The experimental data is shown in Figure 5, where the orange area is where r leads to a flip and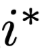 does not, while the blue area is the opposite. However, in most cases, the model’s decision does not flip, indicating that this experiment is not very useful, or further, that simply erasing an intermediate representation does not affect the robustness of the Attention layer, especially when there is a context-related encoder.
Figure 5 Situation of model decision flipping
Jain also designed a set of leave-one-out experiments, using a model framework similar to Serrano’s work, but with an increased number of datasets. The tasks involved text classification, question answering, and natural language inference, with datasets shown in Figure 6, where the text classification tasks were modified into binary classification tasks to simplify the model requirements.
Figure 6 Datasets for text classification, question answering, and natural language inference
Jain believes that the Attention weights learned by the model should be consistent with the importance evaluation indicators of feature representations. The two evaluation indicators compared are the model output results after removing different position intermediate representations and the original output results’ TVD values, where the former’s rationality lies in that if important intermediate representations are removed, the changes in model decision results will be larger, leading to larger corresponding TVD values, while the latter relates to the gradient values obtained by backpropagation for each position. The two indicators are compared with the Attention weights to compute JSD, obtaining corresponding distributions as shown in Figure 7. Here only the data for the gradient indicator is presented, where JSD is converted to relevance, with 0 indicating no correlation and 1 indicating complete consistency. The data for the other indicator is similar, so it will not be elaborated. In general, simply erasing an intermediate representation does not provide strong evidence to prove whether Attention is interpretable.
does not, while the blue area is the opposite. However, in most cases, the model’s decision does not flip, indicating that this experiment is not very useful, or further, that simply erasing an intermediate representation does not affect the robustness of the Attention layer, especially when there is a context-related encoder.
Figure 5 Situation of model decision flipping
Jain also designed a set of leave-one-out experiments, using a model framework similar to Serrano’s work, but with an increased number of datasets. The tasks involved text classification, question answering, and natural language inference, with datasets shown in Figure 6, where the text classification tasks were modified into binary classification tasks to simplify the model requirements.
Figure 6 Datasets for text classification, question answering, and natural language inference
Jain believes that the Attention weights learned by the model should be consistent with the importance evaluation indicators of feature representations. The two evaluation indicators compared are the model output results after removing different position intermediate representations and the original output results’ TVD values, where the former’s rationality lies in that if important intermediate representations are removed, the changes in model decision results will be larger, leading to larger corresponding TVD values, while the latter relates to the gradient values obtained by backpropagation for each position. The two indicators are compared with the Attention weights to compute JSD, obtaining corresponding distributions as shown in Figure 7. Here only the data for the gradient indicator is presented, where JSD is converted to relevance, with 0 indicating no correlation and 1 indicating complete consistency. The data for the other indicator is similar, so it will not be elaborated. In general, simply erasing an intermediate representation does not provide strong evidence to prove whether Attention is interpretable.
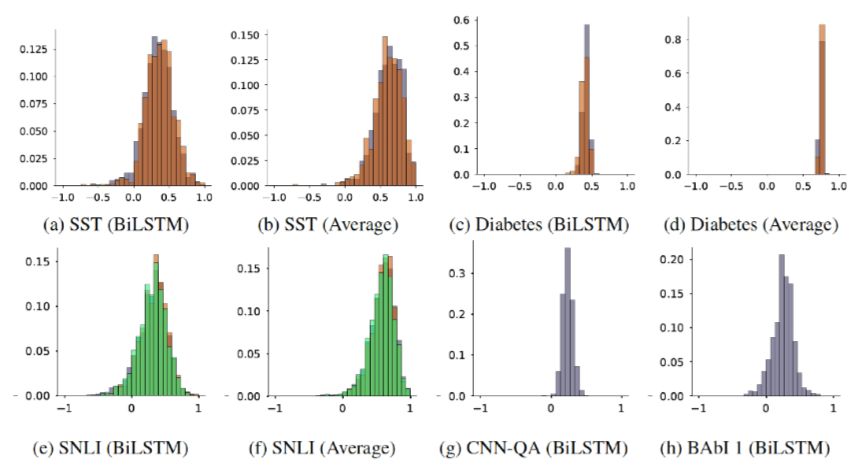 Figure 7 Correlation between Attention distribution and gradient distribution
The idea of Importance is to find a minimal set of intermediate representations to erase that can flip the model’s decision. If the Attention weights for the corresponding positions are the largest, it indicates that the ranking of the importance of Attention weights to intermediate representations is reasonable. The author proposed the following process to verify:
Figure 7 Correlation between Attention distribution and gradient distribution
The idea of Importance is to find a minimal set of intermediate representations to erase that can flip the model’s decision. If the Attention weights for the corresponding positions are the largest, it indicates that the ranking of the importance of Attention weights to intermediate representations is reasonable. The author proposed the following process to verify:
-
Sequentially add Attention weights from largest to smallest to the zeroing set;
-
If the model’s decision flips, stop expanding the set;
-
Check if there is a proper subset that can also flip the model’s decision.
However, the problem here is that finding such a proper subset requires exponential time complexity, which is almost impractical. One can only relax the requirements and find a smaller arbitrary set. The author designed three other ranking schemes to see if the number of elements needed to flip the model’s decision by sequentially setting weights to zero from largest to smallest is smaller than the scheme ranked by Attention weights. The three ranking schemes are as follows:
-
-
Ranking by the size of gradient values backpropagated to the Attention layer;
-
Ranking by the product of gradient values and Attention weights.
These three candidate rankings are not intended to find a Golden Standard erasure combination but to compare with the ranking formed by Attention weights. Additionally, some data items need to be discarded to prevent disrupting the experimental effect, such as in some cases, even when only one intermediate representation is left after erasure, the model’s decision does not flip; or when the input sequence length is 1, ranking is impossible. The results of the experiments are shown in Figure 8, where each rectangle represents the range of data points, and the horizontal line within the rectangle indicates the mean of the data. If there is no marked horizontal line, it indicates that the mean approaches 1. In most cases, the effect of random ranking is far worse than the other three methods, while the data ranges for the other three rankings overlap, but the performance in terms of the mean is generally best for the product of gradient values and Attention weights, followed by ranking by gradient values, and ranking by Attention weights performs the worst.
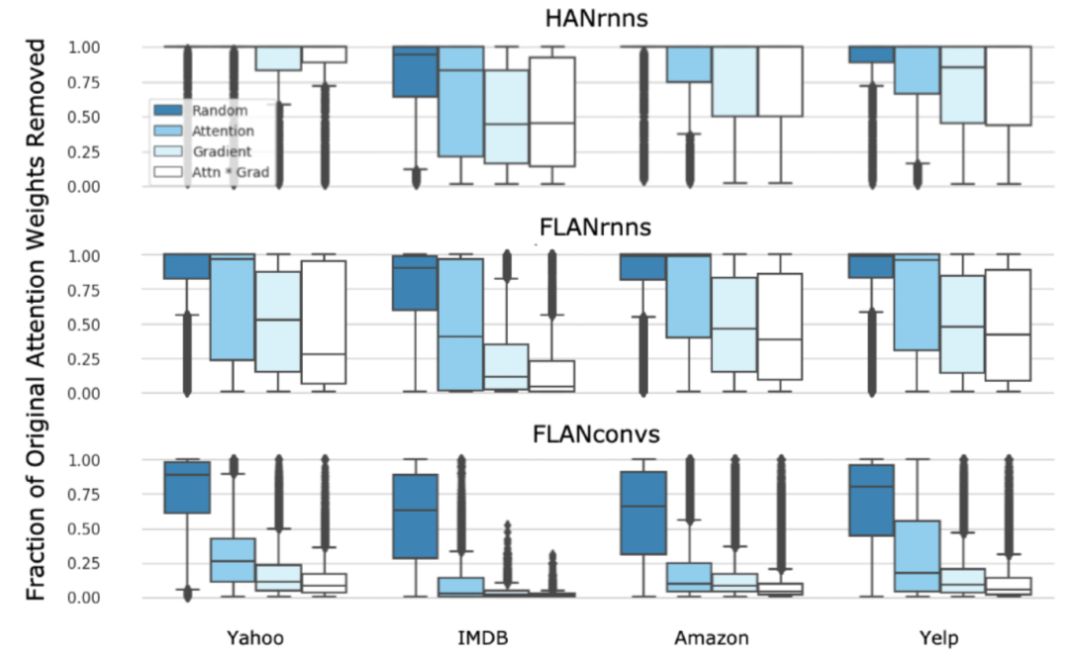 Figure 8 Proportion of Attention weights set to zero to flip model decisions under different ranking rules
The conclusion drawn by the author is that Attention does not maximally describe the model’s decision behavior, and using Attention weights as the basis is effective but not optimal. However, the issue here is that the correlation between setting Attention weights to zero and flipping model decisions is merely an intuitive hypothesis and not a strong prior or axiom.
Figure 8 Proportion of Attention weights set to zero to flip model decisions under different ranking rules
The conclusion drawn by the author is that Attention does not maximally describe the model’s decision behavior, and using Attention weights as the basis is effective but not optimal. However, the issue here is that the correlation between setting Attention weights to zero and flipping model decisions is merely an intuitive hypothesis and not a strong prior or axiom.
3.1.2 Constructing Adversarial Weights
Jain believes that changes in Attention weights should correspondingly affect the model’s predicted results. This idea is similar to flipping model decisions, but the difference is that here the goal is to deceive the model into making the same decision by constructing a set of counterintuitive weight distributions, thereby proving that the Attention mechanism is unreliable.
The adversarial effect that the author wants to construct is shown in Figure 9, illustrating a negative evaluation example. On the left is the original weight learned by the model, with the maximum weight corresponding to the word “waste”, followed by “asking”. The classifier gives a result of 0.01 (0 indicates negative, 1 indicates positive, 0.5 indicates neutral), which aligns with human judgment of the sentence’s sentiment polarity. On the right is the constructed adversarial weight, with the maximum weight corresponding to the word “was”, followed by “myself”, such a counterintuitive Attention method can still lead the classifier to give the same result.
Figure 9 Example of text sentiment analysis
The author designed two construction methods for the experiment. The first is to directly and randomly shuffle the positions of the original Attention weights, and the second is to design a target function to train adversarial weights that yield a model result distribution similar to the original while keeping the Attention weight distribution as different as possible.
Attention Permutation randomly shuffles the Attention weights and observes the changes in model output results, using the TVD metric to evaluate the degree of change. Due to randomness and computational complexity constraints, only 100 random weight groups are tested for each sample, and the median of the calculated TVD metrics is taken for evaluation. As shown in Figure 10, this is a heatmap where the x-axis is the median of model output change degrees, and the y-axis is the maximum value of the original Attention weights. Different colors represent different categories. The author uses the SST dataset as the standard, believing that shuffling Attention does not significantly affect model output results. However, the conclusion of this experiment should be debated, as the author solely attributes the inconsistency of experimental results to the dataset. For example, in the Diabetes dataset, only a few key features can decisively influence the results, while in multiple datasets showing different or even completely opposite results, choosing a dataset that aligns with one’s expectations as a standard is biased, and making conclusions without in-depth research and experimentation is not advisable.
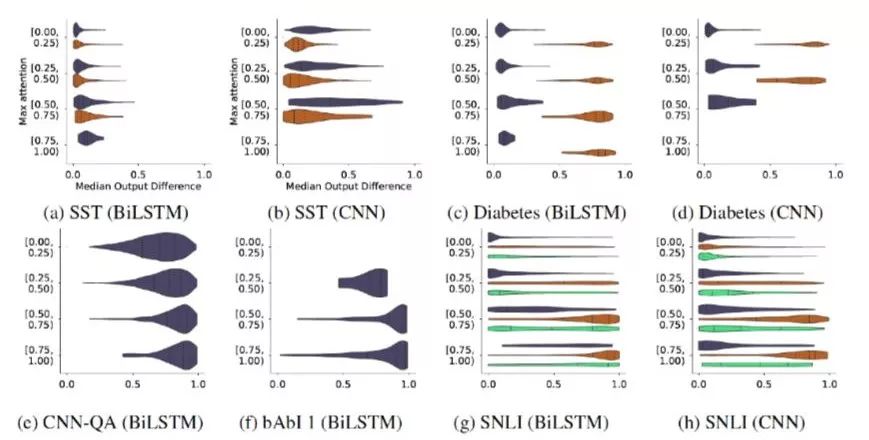 Figure 10 Changes in model output results after random weight shuffling
Adversarial Attention The key experiment conducted by the author is to construct a method for generating adversarial weights, aiming to explicitly find a weight distribution or a group of distributions as different as possible from the original Attention weights while ensuring that the model prediction results remain unchanged. The mathematical expression for the construction method is as follows:
Figure 10 Changes in model output results after random weight shuffling
Adversarial Attention The key experiment conducted by the author is to construct a method for generating adversarial weights, aiming to explicitly find a weight distribution or a group of distributions as different as possible from the original Attention weights while ensuring that the model prediction results remain unchanged. The mathematical expression for the construction method is as follows:
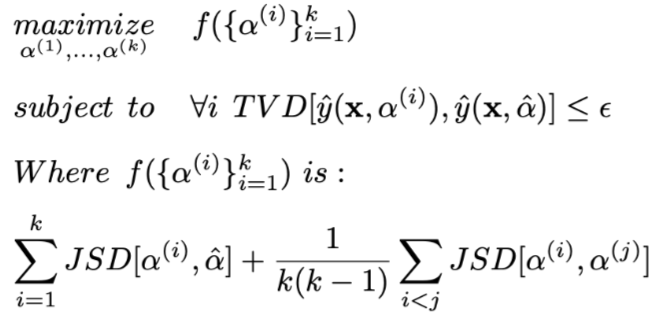 Where
Where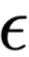 is a precise definition of the small value, indicating the maximum possible TVD distance between the decision made using constructed weights and the result obtained using original weights,
is a precise definition of the small value, indicating the maximum possible TVD distance between the decision made using constructed weights and the result obtained using original weights, is 0.01 for sentiment classification tasks, and 0.05 for question-answering tasks (due to the larger output vector space in question-answering tasks, smaller perturbations can result in larger TVD distances).
is 0.01 for sentiment classification tasks, and 0.05 for question-answering tasks (due to the larger output vector space in question-answering tasks, smaller perturbations can result in larger TVD distances).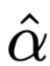 is the original Attention weights,
is the original Attention weights,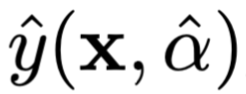 is the result obtained using the original weights.
is the result obtained using the original weights.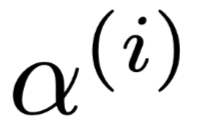 indicates the i-th group of constructed weight distributions,
indicates the i-th group of constructed weight distributions,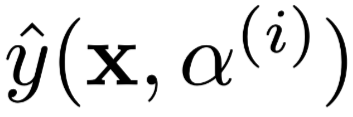 is the model result obtained using the i-th group of constructed weights. The optimization goal is to obtain the generated Attention weights for each group, ensuring that the results produced by the weights do not exceed the specified TVD distance from the original results while maximizing the JS distance between each group of weights and the original weights.
The specific implementation of the optimization goal is
is the model result obtained using the i-th group of constructed weights. The optimization goal is to obtain the generated Attention weights for each group, ensuring that the results produced by the weights do not exceed the specified TVD distance from the original results while maximizing the JS distance between each group of weights and the original weights.
The specific implementation of the optimization goal is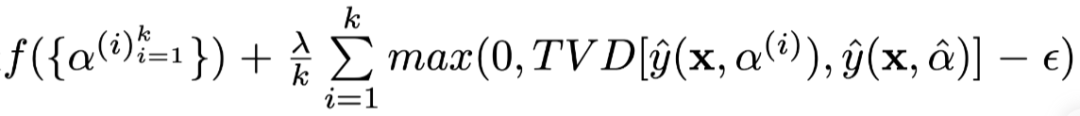 , where λ is a hyperparameter set to 500 during training.
Figure 11 Bar chart of JS distance distribution satisfying constraints
The author continues to consider the relationship between the maximum Attention weight value (to consider the impact of feature effectiveness, i.e., the larger the maximum weight, the more the model focuses on certain features) and the maximum JS distance of the adversarial weights that can be constructed. Intuitively, if the original Attention weight distribution is steeper, then it becomes more difficult to generate effective (large JSD value) adversarial weights. As shown in Figure 12, this is also a heatmap where the x-axis is the maximum JS distance and the y-axis is the maximum original Attention weight. The author believes that although there is indeed a trend as previously mentioned, it cannot be denied that there are indeed many examples in each dataset where high original Attention weights can still construct adversarial weights with large JS distances, meaning that the assertion that a specific set of features can fully influence the results is misleading.
, where λ is a hyperparameter set to 500 during training.
Figure 11 Bar chart of JS distance distribution satisfying constraints
The author continues to consider the relationship between the maximum Attention weight value (to consider the impact of feature effectiveness, i.e., the larger the maximum weight, the more the model focuses on certain features) and the maximum JS distance of the adversarial weights that can be constructed. Intuitively, if the original Attention weight distribution is steeper, then it becomes more difficult to generate effective (large JSD value) adversarial weights. As shown in Figure 12, this is also a heatmap where the x-axis is the maximum JS distance and the y-axis is the maximum original Attention weight. The author believes that although there is indeed a trend as previously mentioned, it cannot be denied that there are indeed many examples in each dataset where high original Attention weights can still construct adversarial weights with large JS distances, meaning that the assertion that a specific set of features can fully influence the results is misleading.
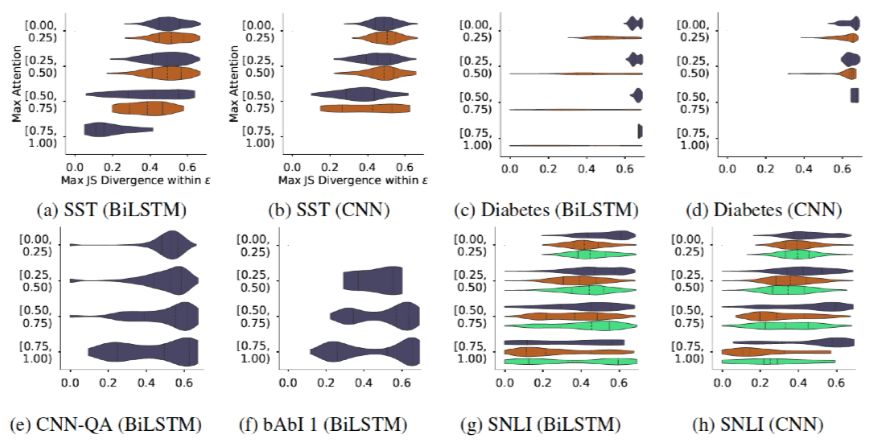 Figure 12 Relationship between JS distance and maximum original Attention weight distribution
To summarize the above conclusions, Serrano designed multiple experiments around intermediate representation erasure, observing the changes in model decisions, and concluded that: ‘Attention does not necessarily correspond to importance.’, because in the experiments, Attention often fails to successfully identify the most important intermediate representations that affect model decisions. Additionally, there is a significant but unverified hypothesis: ‘Attention magnitudes do seem more helpful in uncontextualized cases.’, meaning that the context-related encoder may make the Attention mechanism difficult to interpret, but the author did not conduct in-depth research on this.
Jain, on the other hand, raised two questions based on the contribution of Attention to the model’s transparency:
Figure 12 Relationship between JS distance and maximum original Attention weight distribution
To summarize the above conclusions, Serrano designed multiple experiments around intermediate representation erasure, observing the changes in model decisions, and concluded that: ‘Attention does not necessarily correspond to importance.’, because in the experiments, Attention often fails to successfully identify the most important intermediate representations that affect model decisions. Additionally, there is a significant but unverified hypothesis: ‘Attention magnitudes do seem more helpful in uncontextualized cases.’, meaning that the context-related encoder may make the Attention mechanism difficult to interpret, but the author did not conduct in-depth research on this.
Jain, on the other hand, raised two questions based on the contribution of Attention to the model’s transparency:
-
To what extent are Attention weights correlated with feature importance metrics?
-
Do different weight distributions necessarily lead to different model decisions?
The answers provided are as follows:
-
‘Only weakly and inconsistently’, the correlation between Attention weights and feature importance metrics (gradient distributions, changes in model results after removing a certain intermediate representation) is not significant and unstable;
-
‘It is very possible to construct adversarial attention distributions that yield effectively equivalent predictions.’, it is easy to construct adversarial weights that focus on features completely different from the original weights, and furthermore, setting weights randomly often does not significantly impact the model’s decision results.
3.2 Not Not Explanation
This section titled Not Not Explanation is a rebuttal to the previous arguments regarding the non-interpretability of Attention, not a proof of the interpretability of Attention. Here, the main reference is Wiegreffe’s rebuttal to Jain. Wiegreffe mainly provides two reasons:
-
Attention Distribution is not a Primitive. The distribution of Attention weights does not exist independently, as the parameters of the Attention layer cannot be isolated from the entire model due to the forward and backward propagation processes; otherwise, it loses its practical significance;
-
Existence does not Entail Exclusivity. The existence of Attention distributions does not imply exclusivity; Attention merely provides an explanation rather than a unique explanation. Especially when the dimensionality of intermediate representations is large while the output categories are few, the dimensionality reduction mapping function can easily exhibit considerable flexibility.
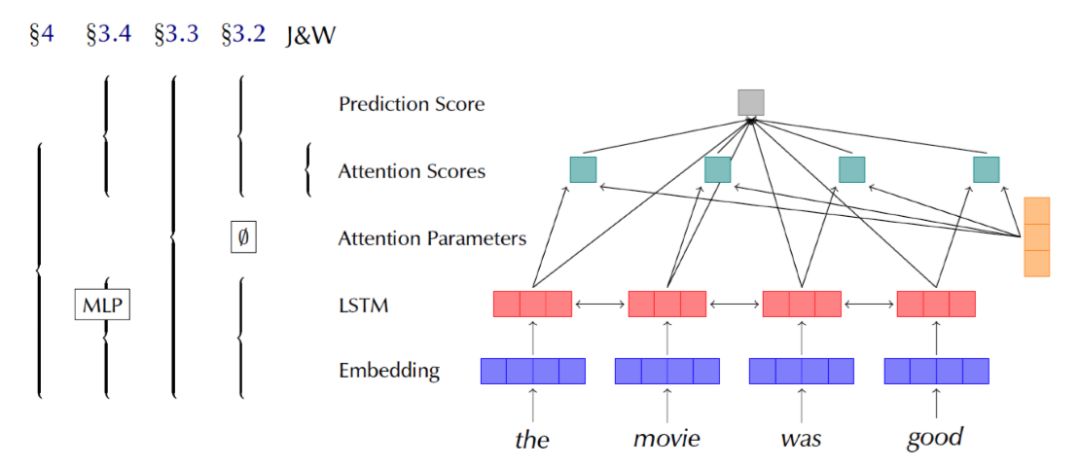
The author designed four sets of control experiments for rebuttal, as shown in Figure 13. The right side shows the model used, which is consistent with the previously introduced model, including embedding layers, encoding layers, and independent Attention layers, with the task also being text classification. The left side corresponds to the ranges involved in each experiment. J&W refers to Jain’s experiment, which only involves modifying Attention weights. It is important to note that the Attention Parameters in the figure represent the parameters trained by the Attention layer, and the final α weights are calculated from them. The four experiments from right to left are:
-
Uniform as Adversary. Train a baseline model with fixed average Attention weights;
-
Variance with a Model. Use a randomly initialized model retrained to serve as a normal baseline for Attention weight distribution deviations;
-
Diagnosing Attention Distribution by Guiding Simpler Models. Implement a diagnostic framework using fixed pre-trained Attention weights;
-
Training an Adversary. Design an end-to-end adversarial weight training method, noting that this is not an independent experiment but a specific implementation of the adversarial weight generation from the previous experiment.
Figure 13 Results of the model used and the control experiment section
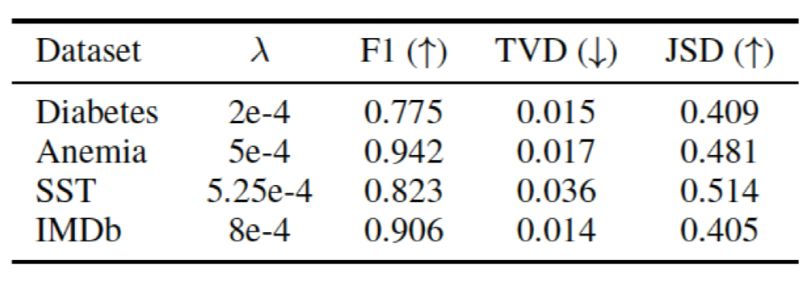
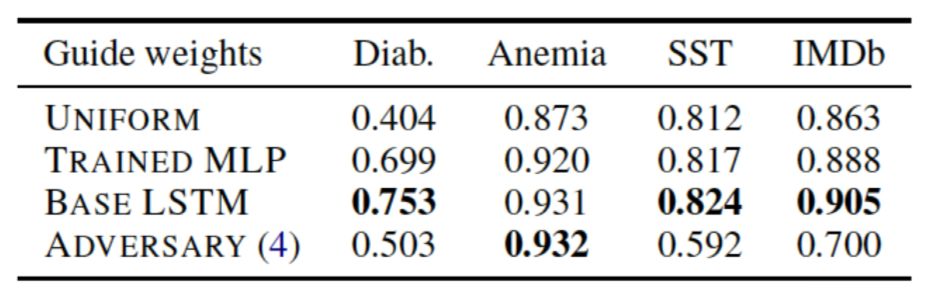
Uniform as Adversary. The intent of this experiment is to verify whether the Attention mechanism is necessary across various datasets, as if the task is too simple and does not require Attention to achieve good results, then this data group is not persuasive. Conversely, if Attention is necessary, removing it would lead to a significant decline in model performance. The experimental design is straightforward: directly set the Attention weights to their average and freeze them, training only the remaining parts, with all intermediate representations input from the encoding layer directly calculating the average as the output of the Attention layer. The text classification F1 metrics obtained are shown in Figure 14, where the leftmost is the result given by Jain, the middle is Wiegreffe’s reproduced result, and the rightmost is the result obtained from this experiment. Intuitively, it can be seen that for most of the datasets, the effect of using Attention does not significantly improve results, especially for the last two datasets, where there is almost no increase. The author summarizes this as ‘Attention is not explanation if you don’t need it.’
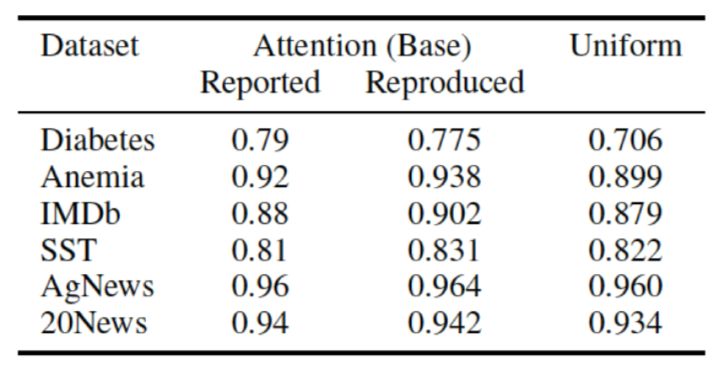 Figure 14 F1 metrics for text classification tasks
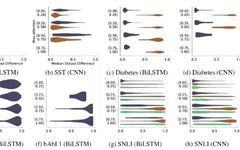
Variance with a Model. The author uses a randomly seeded model to retrain and obtain different Attention weights, which are viewed as normal weights, meaning they are merely disturbed by noise rather than artificially intervened non-adversarial weights. By calculating the JSD metric between the distributions of the normal weights and the original weights, a normal baseline is obtained, and weights exceeding this baseline are considered abnormal. As shown in Figure 15, this is a set of comparative graphs where the x-axis is the JS distance and the y-axis is the range of maximum Attention weights. From a to d are the baselines generated using random seeds for various datasets, while e and f are the adversarial weight experimental data from Jain. It can be observed that the generated weights on the SST dataset far exceed the baseline. This indicates that artificially constructed adversarial data is indeed abnormal, surpassing the degree of noise, and this result coincides with the previous experiment’s phenomenon that the less effect Attention has, the more unpredictable its weight distribution becomes. However, up to this point, it remains a theoretical discussion without precise data to explain the situation of the constructed Attention weights.
Figure 14 F1 metrics for text classification tasks
Variance with a Model. The author uses a randomly seeded model to retrain and obtain different Attention weights, which are viewed as normal weights, meaning they are merely disturbed by noise rather than artificially intervened non-adversarial weights. By calculating the JSD metric between the distributions of the normal weights and the original weights, a normal baseline is obtained, and weights exceeding this baseline are considered abnormal. As shown in Figure 15, this is a set of comparative graphs where the x-axis is the JS distance and the y-axis is the range of maximum Attention weights. From a to d are the baselines generated using random seeds for various datasets, while e and f are the adversarial weight experimental data from Jain. It can be observed that the generated weights on the SST dataset far exceed the baseline. This indicates that artificially constructed adversarial data is indeed abnormal, surpassing the degree of noise, and this result coincides with the previous experiment’s phenomenon that the less effect Attention has, the more unpredictable its weight distribution becomes. However, up to this point, it remains a theoretical discussion without precise data to explain the situation of the constructed Attention weights.
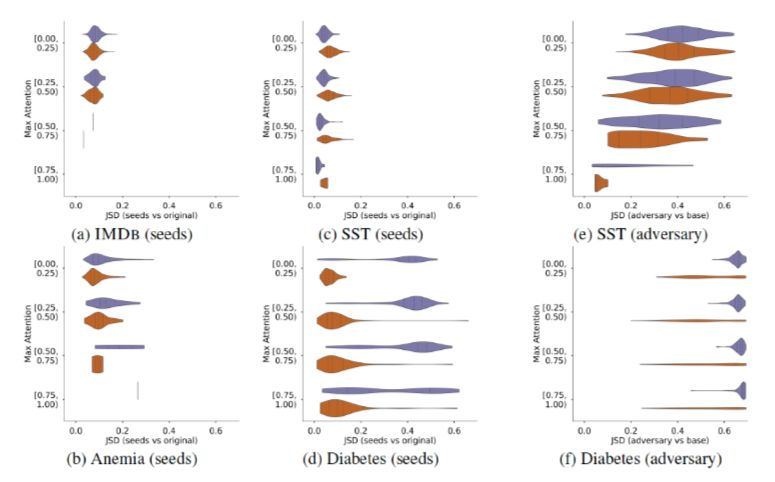 Figure 15 Comparison of the JS distances between the weight distributions generated based on random seed initialization and adversarial weights to the original distribution
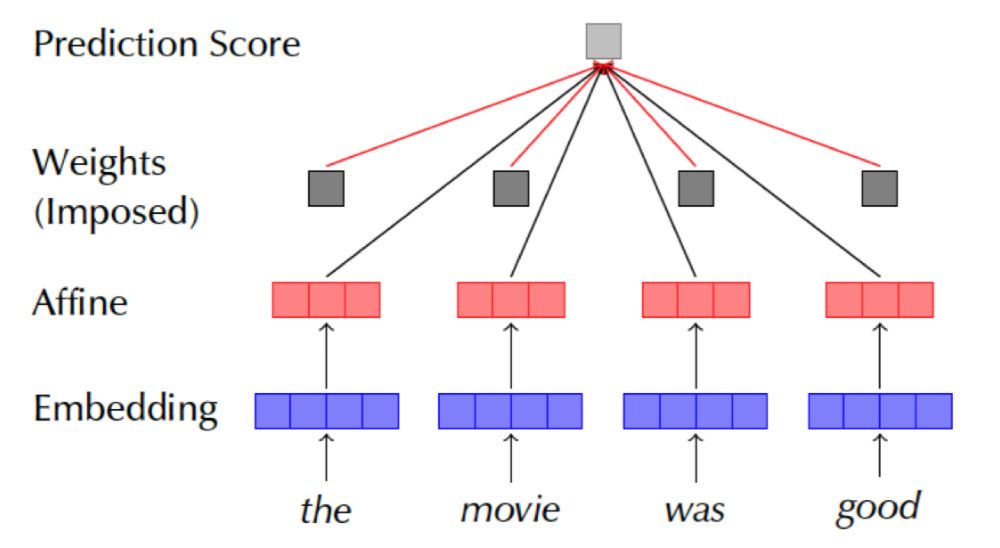
Diagnosing Attention Distribution by Guiding Simpler Models. This part of the model differs from the previous ones, as it aims to more accurately examine the Attention weight distribution, eliminating the influence of context-related structures. Thus, the previously used LSTM encoding layer is removed, and only an MLP is used to complete the affine transformation from the embedding layer to the classification result. Subsequently, fixed non-trainable Attention weights are directly used to obtain model decision results through weighted summation, with the specific model shown in Figure 16. The author designs four sets of control experiments based on this:
Figure 15 Comparison of the JS distances between the weight distributions generated based on random seed initialization and adversarial weights to the original distribution
Diagnosing Attention Distribution by Guiding Simpler Models. This part of the model differs from the previous ones, as it aims to more accurately examine the Attention weight distribution, eliminating the influence of context-related structures. Thus, the previously used LSTM encoding layer is removed, and only an MLP is used to complete the affine transformation from the embedding layer to the classification result. Subsequently, fixed non-trainable Attention weights are directly used to obtain model decision results through weighted summation, with the specific model shown in Figure 16. The author designs four sets of control experiments based on this:
-
The preset Attention weights are set to average as a baseline;
-
Weights are not fixed, allowing them to be trained together with the MLP;
-
Directly use the original Attention weights from when LSTM was used as the encoder;
-
Use the adversarially generated Attention weights (implemented in the next section).
Figure 16 Model using preset Attention weights
The results of the four sets of control experiments are shown in Figure 17, where replacing the original Attention weights with those that are trained together with the MLP enhances performance. Additionally, in the first experiment, the effect of adversarial weights is far lower than that of original weights on datasets where Attention weights are meaningful, indicating that the importance information encoded by the Attention mechanism is not independent of the model and can be transferred to other models when using the same dataset. However, the constructed adversarial weights do not discover additional information about the data but merely exploit specific model vulnerabilities (the model’s capability exceeds the task’s requirements).
Figure 17 F1 metrics obtained from four sets of control experiments
Train an Adversary. This is the specific generation model for adversarial weights, which mainly differs from Jain’s proposed model in the loss function:
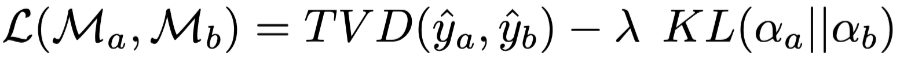 , where
, where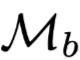 is the model with original weights, and
is the model with original weights, and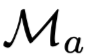 is the model with adversarial weights. As shown in Figure 18, it is indeed possible to obtain good adversarial weights, but it has also been proven in the previous experiment that these weights merely exploit the model’s vulnerabilities and do not uncover more important information.
is the model with adversarial weights. As shown in Figure 18, it is indeed possible to obtain good adversarial weights, but it has also been proven in the previous experiment that these weights merely exploit the model’s vulnerabilities and do not uncover more important information.
4. Conclusion
The interpretability of the Attention mechanism is currently a hot topic, with many authors designing various experiments to prove or disprove it, yet there are always some incomplete aspects, such as issues with datasets, model designs, and sometimes even disagreements on the definition of interpretability. Regardless, a step-by-step thorough exploration is always necessary. Whether it is the intermediate representation erasure experiment designed by Serrano or the adversarial weight generation experiment by Jain, the ultimate goal is to find examples where Attention weights do not accurately express token importance. Both perspectives are limited to the Attention weights themselves, overlooking many factors that significantly influence results, such as whether the dataset requires the Attention mechanism and the effects of context-related encoders on Attention weights, all of which could undermine the experiments’ validity. Wiegreffe has effectively rebutted the design flaws in Jain’s experiments, but the reliability of the method for testing transferred Attention weights still needs further discussion.
Moreover, many questions have only been raised but not explored:
-
What kinds of tasks require the Attention mechanism, and is it universal?
-
What impact does the choice of encoding layer have on Attention?
-
Is it reasonable to transfer Attention weights between different models on the same dataset?
-
How do the complexities of models and datasets affect the ease of constructing adversarial weights?
Additionally, Serrano has proposed some prospects. Currently, research is still limited to importance based on Argmax; everyone only considers the impact of Attention weights on the model’s final decision results, but that is not all, as there may be cases where a particular feature reduces the probability of a certain category appearing. This means that every item in the output Softmax function has research value, not just the one with the highest probability as the result.
Finally, let us look forward to what new progress the ACL 2020, due by December, will bring us.
References:
[1] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Łukasz Kaiser, and Illia Polosukhin. 2017. Attention is all you need. Advances in neural information processing systems, pp. 5998-6008.
[2] Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2019. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), pp. 4171-4186.
[3] Dzmitry Bahdanau, Kyunghyun Cho, and Yoshua Bengio. 2015. Neural machine translation by jointly learning to align and translate. In Proceedings of the International Conference on Learning Representations.
[4] Sofia Serrano, and Noah A. Smith. 2019. Is Attention Interpretable. arXiv preprint arXiv:1906.03731.
[5] Sarthak Jain and Byron C. Wallace. 2019. Attention is not Explanation. InProceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers).
[6] Sarah Wiegreffe, and Yuval Pinter. 2019. Attention is not not Explanation.arXiv preprint arXiv:1908.04626.
[7] Zichao Yang, Diyi Yang, Chris Dyer, Xiaodong He, Alex Smola, and Eduard Hovy. 2016. Hierarchical attention networks for document classification. InProceedings of the Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies.
[8] Yoon Kim. 2014. Convolutional neural networks for sentence classification. InProceedings of the Conference on Empirical Methods in Natural Language Processing.
[9] Zachary C Lipton. 2016. The mythos of model interpretability. arXiv preprint arXiv:1606.03490.
Source References:
NAACL 2019 “Attention is Not Explanation”
ACL 2019 “Is Attention Interpretable?”
EMNLP 2019 “Attention is Not Not Explanation”

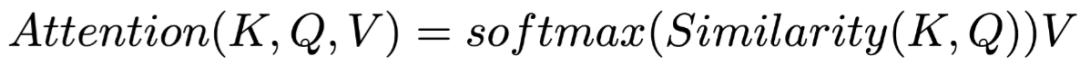
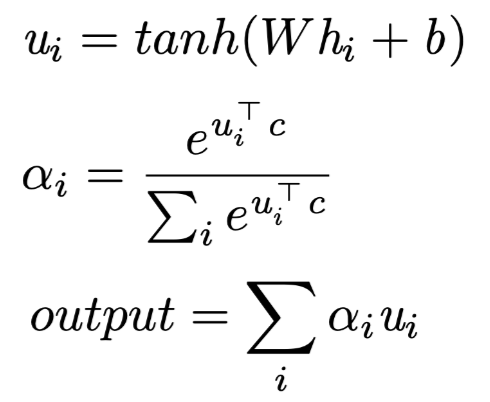
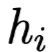 (As Value) is the output tensor at the i-th position in the sequence from the previous layer. If the previous layer is a bidirectional RNN structure, then
(As Value) is the output tensor at the i-th position in the sequence from the previous layer. If the previous layer is a bidirectional RNN structure, then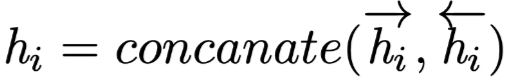 ;
;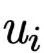 is the key Key at the i-th position, calculated from the value Value through a fully connected layer;
is the key Key at the i-th position, calculated from the value Value through a fully connected layer;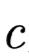 is the query Query of this Attention layer, initialized randomly and updated synchronously during training. If Attention is not a standalone layer but is built on the decoder, then
is the query Query of this Attention layer, initialized randomly and updated synchronously during training. If Attention is not a standalone layer but is built on the decoder, then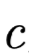 is related to the output at the corresponding position during the encoding phase; the similarity function is matrix dot product, and the resulting
is related to the output at the corresponding position during the encoding phase; the similarity function is matrix dot product, and the resulting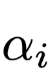 is the Attention weight,
is the Attention weight,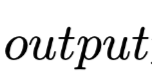 is the output of the Attention layer.
is the output of the Attention layer.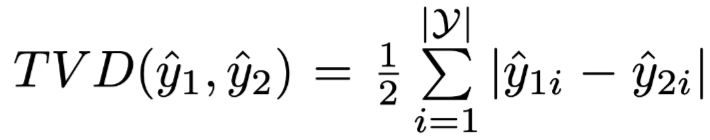
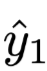 and
and 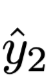 are two different output result distributions.
are two different output result distributions.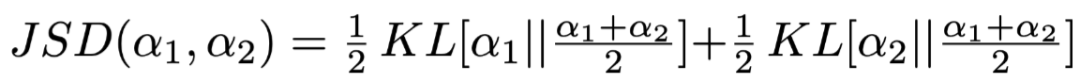
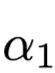 and
and 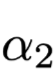 are two different distributions, which can be either output results or Attention weights,
are two different distributions, which can be either output results or Attention weights,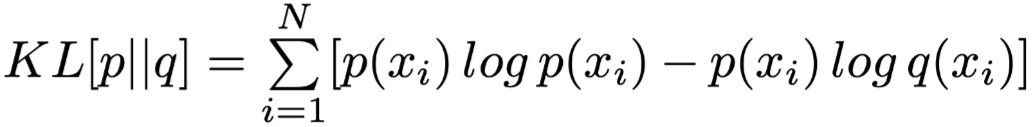


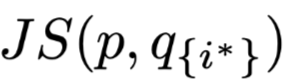 , where
, where is the distribution of the normal result,
is the distribution of the normal result,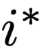 is the result distribution after erasing the highest weight’s corresponding intermediate representation. To verify how much this distance is, a random position is selected
is the result distribution after erasing the highest weight’s corresponding intermediate representation. To verify how much this distance is, a random position is selected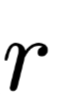 , and using the same process to erase the intermediate representation, the corresponding JSD metric is obtained
, and using the same process to erase the intermediate representation, the corresponding JSD metric is obtained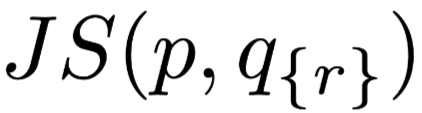 . Intuitively, if the items with high weights are indeed more important, then this formula should always be positive, and the difference in the two weights set to zero
. Intuitively, if the items with high weights are indeed more important, then this formula should always be positive, and the difference in the two weights set to zero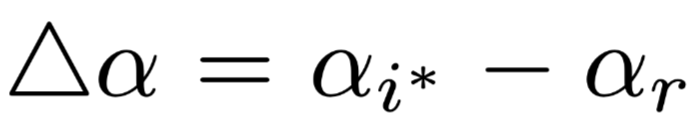 should be larger, and the value of
should be larger, and the value of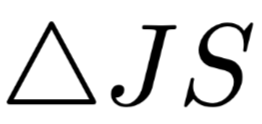 should be larger as well. The charts presented by the author in the text are shown in Figure 4 on the left, where the x-axis is the difference between the two weights, and the y-axis is the value of
should be larger as well. The charts presented by the author in the text are shown in Figure 4 on the left, where the x-axis is the difference between the two weights, and the y-axis is the value of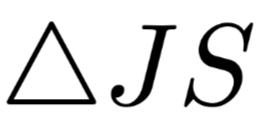 . The author states that there are almost no negative results in the data obtained, and even if there are, they are close to 0. Moreover, as the difference between the two weights increases, the degree of change in the model’s output result distribution also increases accordingly. However, the author believes that “even if the difference between the two weights reaches 0.4 (where the weights satisfy the sum normalization), most positive
. The author states that there are almost no negative results in the data obtained, and even if there are, they are close to 0. Moreover, as the difference between the two weights increases, the degree of change in the model’s output result distribution also increases accordingly. However, the author believes that “even if the difference between the two weights reaches 0.4 (where the weights satisfy the sum normalization), most positive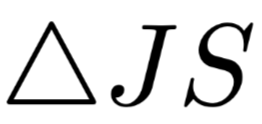 values are still very close to 0,” thus preliminarily believing that the Attention mechanism has phenomena that contradict intuition.
values are still very close to 0,” thus preliminarily believing that the Attention mechanism has phenomena that contradict intuition.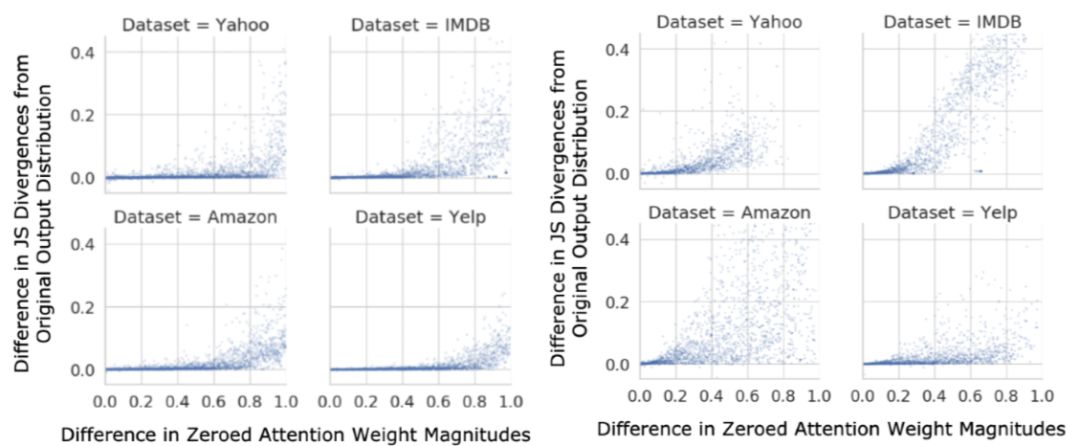
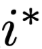 and randomly selected positions
and randomly selected positions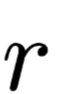 after erasing the intermediate representations, and observing the changes in model decision behavior. The experimental data is shown in Figure 5, where the orange area is where r leads to a flip and
after erasing the intermediate representations, and observing the changes in model decision behavior. The experimental data is shown in Figure 5, where the orange area is where r leads to a flip and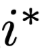 does not, while the blue area is the opposite. However, in most cases, the model’s decision does not flip, indicating that this experiment is not very useful, or further, that simply erasing an intermediate representation does not affect the robustness of the Attention layer, especially when there is a context-related encoder.
does not, while the blue area is the opposite. However, in most cases, the model’s decision does not flip, indicating that this experiment is not very useful, or further, that simply erasing an intermediate representation does not affect the robustness of the Attention layer, especially when there is a context-related encoder.




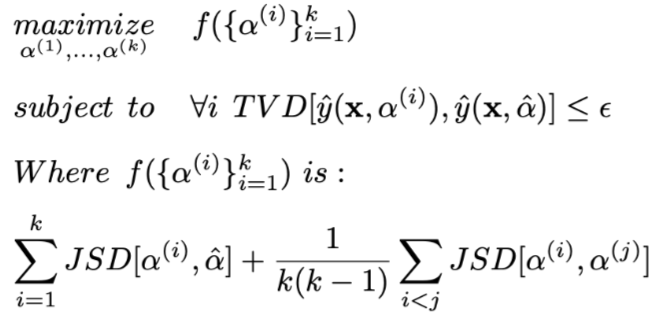
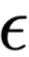 is a precise definition of the small value, indicating the maximum possible TVD distance between the decision made using constructed weights and the result obtained using original weights,
is a precise definition of the small value, indicating the maximum possible TVD distance between the decision made using constructed weights and the result obtained using original weights, is 0.01 for sentiment classification tasks, and 0.05 for question-answering tasks (due to the larger output vector space in question-answering tasks, smaller perturbations can result in larger TVD distances).
is 0.01 for sentiment classification tasks, and 0.05 for question-answering tasks (due to the larger output vector space in question-answering tasks, smaller perturbations can result in larger TVD distances).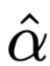 is the original Attention weights,
is the original Attention weights,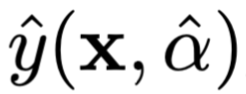 is the result obtained using the original weights.
is the result obtained using the original weights.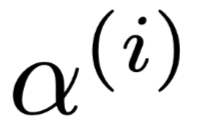 indicates the i-th group of constructed weight distributions,
indicates the i-th group of constructed weight distributions,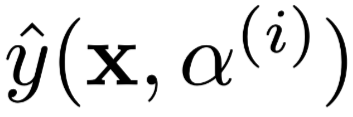 is the model result obtained using the i-th group of constructed weights. The optimization goal is to obtain the generated Attention weights for each group, ensuring that the results produced by the weights do not exceed the specified TVD distance from the original results while maximizing the JS distance between each group of weights and the original weights.
is the model result obtained using the i-th group of constructed weights. The optimization goal is to obtain the generated Attention weights for each group, ensuring that the results produced by the weights do not exceed the specified TVD distance from the original results while maximizing the JS distance between each group of weights and the original weights.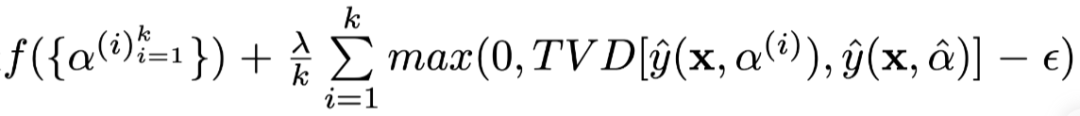 , where λ is a hyperparameter set to 500 during training.
, where λ is a hyperparameter set to 500 during training.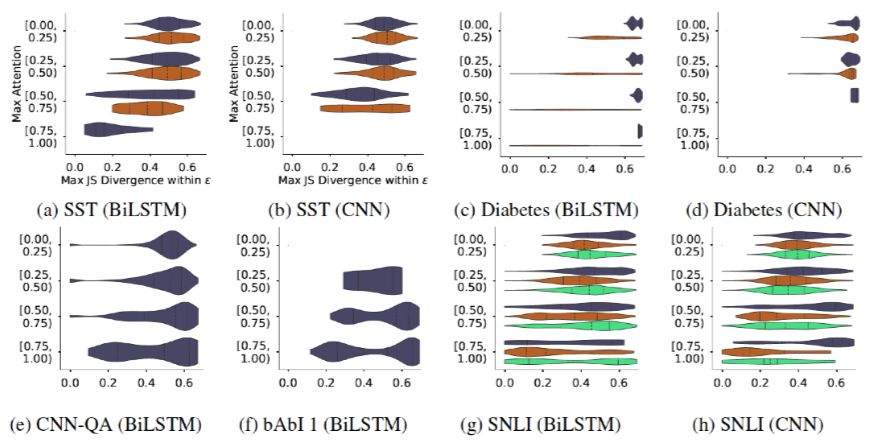



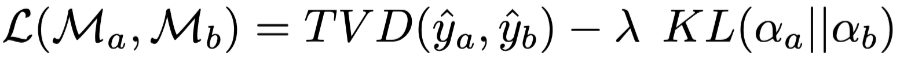 , where
, where is the model with original weights, and
is the model with original weights, and is the model with adversarial weights. As shown in Figure 18, it is indeed possible to obtain good adversarial weights, but it has also been proven in the previous experiment that these weights merely exploit the model’s vulnerabilities and do not uncover more important information.
is the model with adversarial weights. As shown in Figure 18, it is indeed possible to obtain good adversarial weights, but it has also been proven in the previous experiment that these weights merely exploit the model’s vulnerabilities and do not uncover more important information.