Can Embedded Vectors Understand Numbers? BERT vs. ELMo

Selected from arXiv

Authors:Eric Wallace et al.

Translation by Machine Heart

Contributors:Mo Wang

Performing numerical reasoning on natural language text is a long-standing challenge for end-to-end models. Researchers from the Allen Institute for AI, Peking University, and the University of California, Irvine, attempt to explore whether “out-of-the-box” neural NLP models can solve this problem, and how they do so.

Paper: Do NLP Models Know Numbers? Probing Numeracy in Embeddings
Paper link: https://arxiv.org/pdf/1909.07940.pdf

The ability to understand and process numbers (numeracy) is crucial for many complex reasoning tasks. Currently, most natural language processing models treat numbers in text the same way as other tokens: as distributed vectors. But is this sufficient to capture numbers?

Researchers investigated the numerical reasoning capabilities of the current state-of-the-art question-answering models on the DROP dataset, finding that the model excels at solving problems requiring numerical reasoning, meaning it is able to capture numbers.

To understand the source of this capability, researchers tested token embedding methods such as BERT and GloVe on synthetic list maximum, number decoding, and addition tasks. Surprisingly, standard embedding methods naturally possess a high degree of numeracy. For instance, GloVe and word2vec can accurately encode numbers up to thousands. Character-level embeddings are even more accurate—among all pre-trained methods, ELMo has the strongest numeric capturing ability, while the BERT model using subword units is less accurate than ELMo.

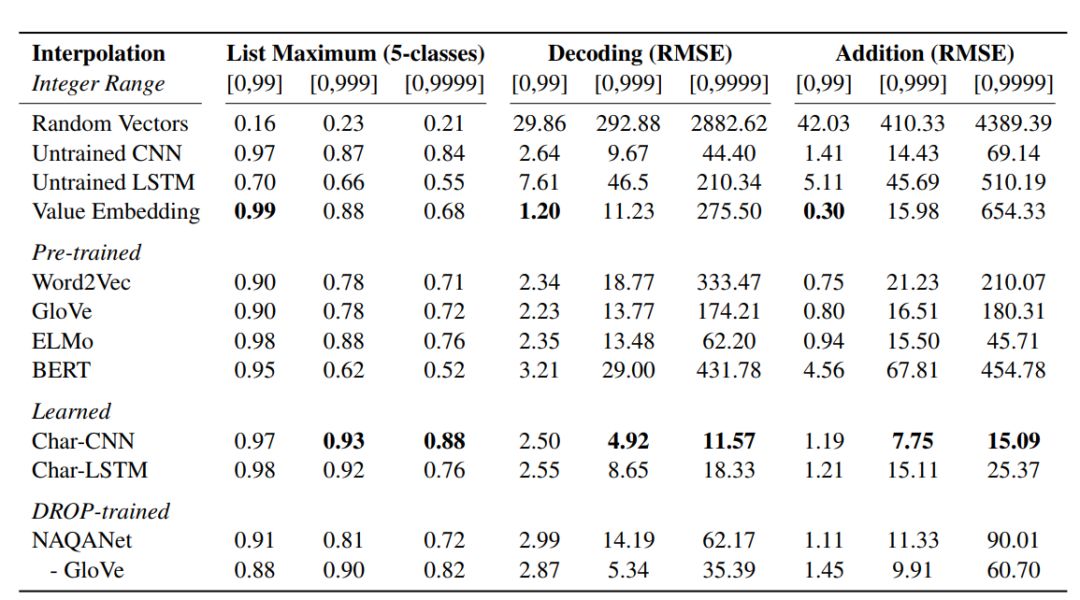
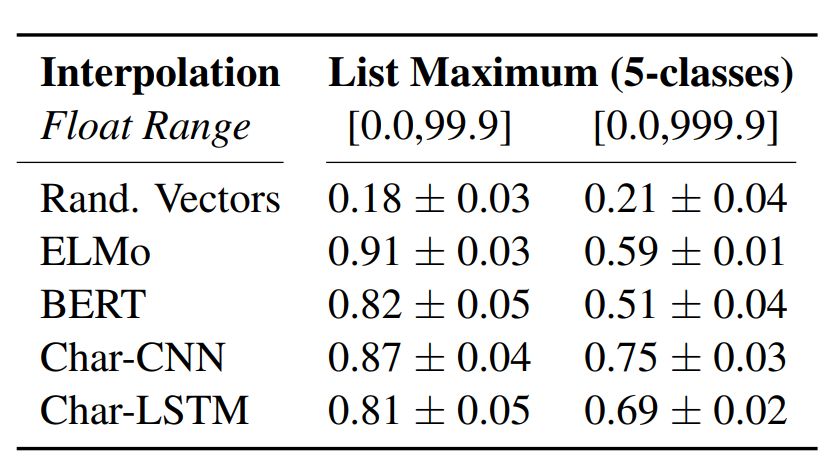
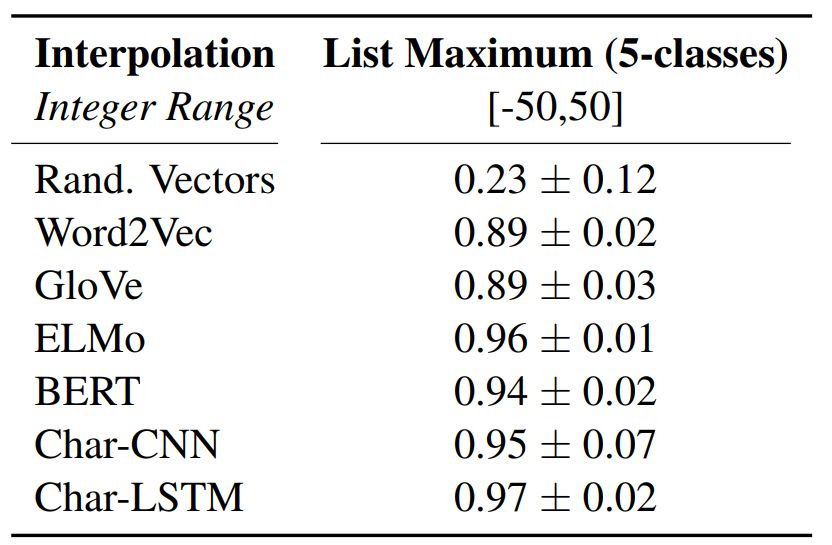
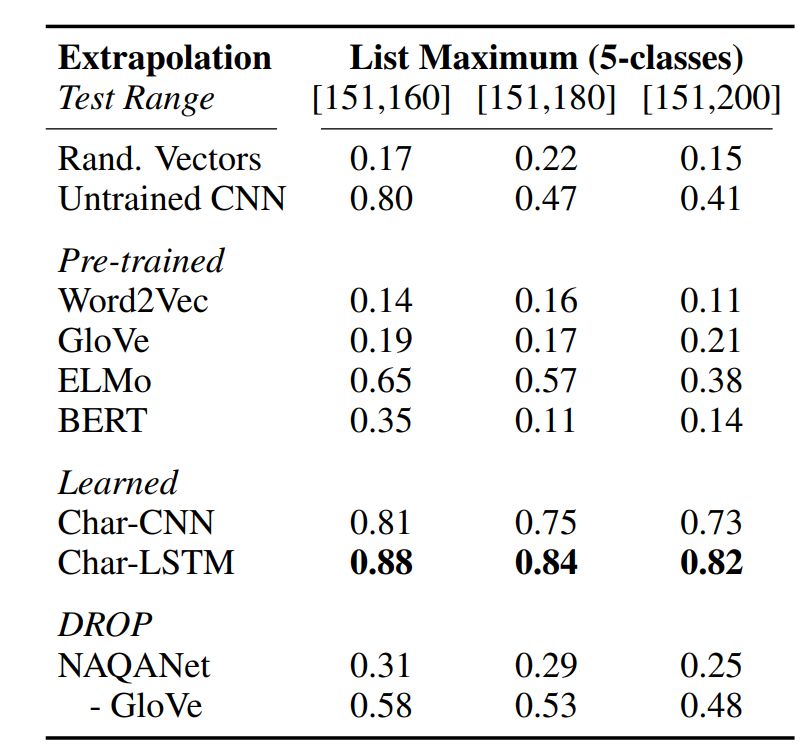
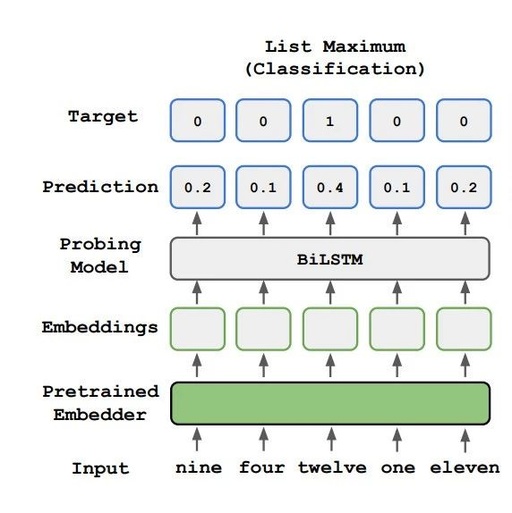
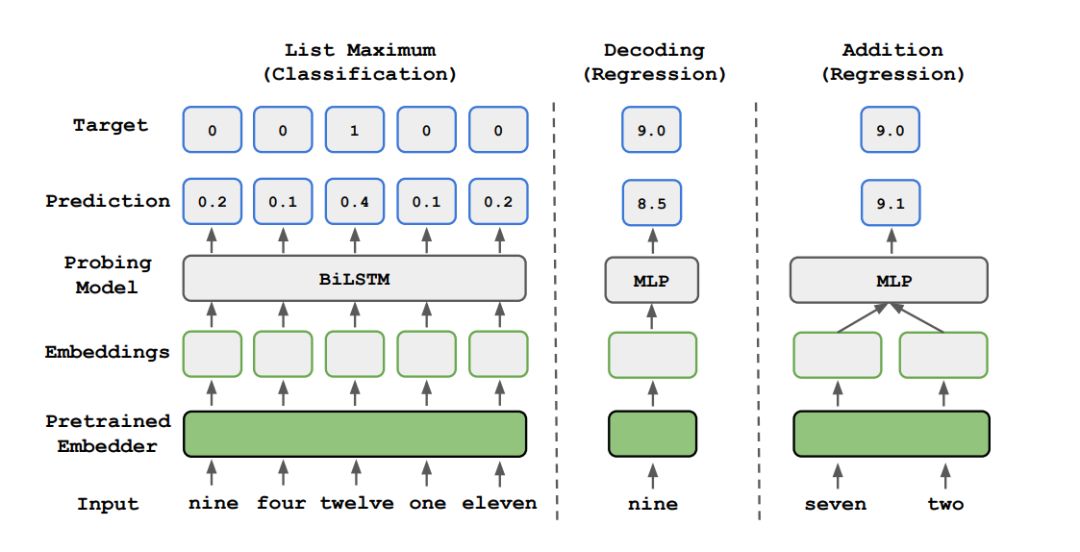
Can Embedded Vectors Understand Numbers? BERT vs. ELMo

Figure 1:Researchers trained a probing model based on word embeddings to decode random integers within the range of [-500, 500], such as “71” → 71.0.

Researchers plotted the model’s predictions for all numbers in the range of [-2000, 2000]. The model accurately decoded numbers within the training range (blue), meaning pre-trained embeddings (such as GloVe and BERT) can capture numbers. However, the probing model struggles with larger numbers (red). Char-CNN (e) and Char-LSTM (f) were jointly trained using the probing model.

The Importance of “Numeracy” in NLP Models

The first step in performing numerical reasoning on natural language is numeracy: understanding and processing numbers in numeric or textual form. For example, you must understand that “23” is greater than “twenty-two.” When a number appears (possibly implicitly), reasoning algorithms can process the text, such as extracting a list of scores and calculating the maximum (the first question in Figure 2). Performing numerical reasoning on paragraphs with only question-answer supervision has been a long-standing challenge for end-to-end models, and this study attempts to explore whether “out-of-the-box” neural NLP models have learned and how they learn to solve this problem.

Figure 2:Three DROP questions requiring numerical reasoning, with the current state-of-the-art NAQANet model accurately answering each question.(The possible answers for each question are underlined, and the model’s predictions are shown in bold.)

Researchers first analyzed the current state-of-the-art NAQANet model on the DROP dataset, testing the model on a subset of numerical reasoning problems. Surprisingly, the model exhibited excellent numerical reasoning capabilities. When reading and understanding natural language, the model successfully calculated the maximum/minimum of a score list, extracted the highest-ranked entity (superlative entity, argmax reasoning), and compared values.

For example, although NAQANet achieved only a 49 F1 score across the entire validation set, it scored an 89 F1 score on numerical comparison problems. Researchers also conducted model tests by perturbing validation paragraphs and discovered a failure mode: the model struggles to infer numbers outside the training range.

Researchers were very curious about how well the model learns numbers, specifically how it understands values based on embeddings. The model uses standard embeddings (GloVe a and Char-CNN) and does not receive direct supervision signals regarding the size/order of numbers. To understand how it masters numeracy, researchers explored token embedding methods (such as BERT and GloVe) in synthetic list maximum, number decoding, and addition tasks.

Research found that all widely used pre-trained embedding methods (such as ELMo, BERT, and GloVe) can capture numbers: the size of numbers can be represented in embeddings, even for numbers up to thousands. Among all embeddings, character-level methods have a stronger numeracy capability than word-level or subword-level methods, with ELMo outperforming BERT. Directly learned character-level models are overall the strongest in comprehensive tasks. Finally, researchers investigated why NAQANet struggles with extrapolation, whether it is a model issue or an embedding issue. They repeated probing tasks and tested the model’s extrapolation, finding that neural networks have difficulties predicting numbers outside the training range.

How Strong is the Numeracy Ability of Embeddings?

Researchers explored the numeracy abilities of token embeddings using comprehensive numerical tasks, considering three comprehensive tasks (see Figure 3).

Figure 3:Exploration setup.Researchers input numbers into pre-trained embedding models (such as BERT and GloVe) and train a probing model to solve numerical tasks, such as finding the maximum in a list, decoding numbers, or performing addition.

If the probing model can generalize to held-out numbers, then the pre-trained embeddings must contain numerical information. Researchers provided several forms of numbers: words, numeric (9), floating-point (9.1), or negative numbers (-9).

List maximum: Given an embedding list containing 5 numbers, the task is to predict the index of the maximum value.
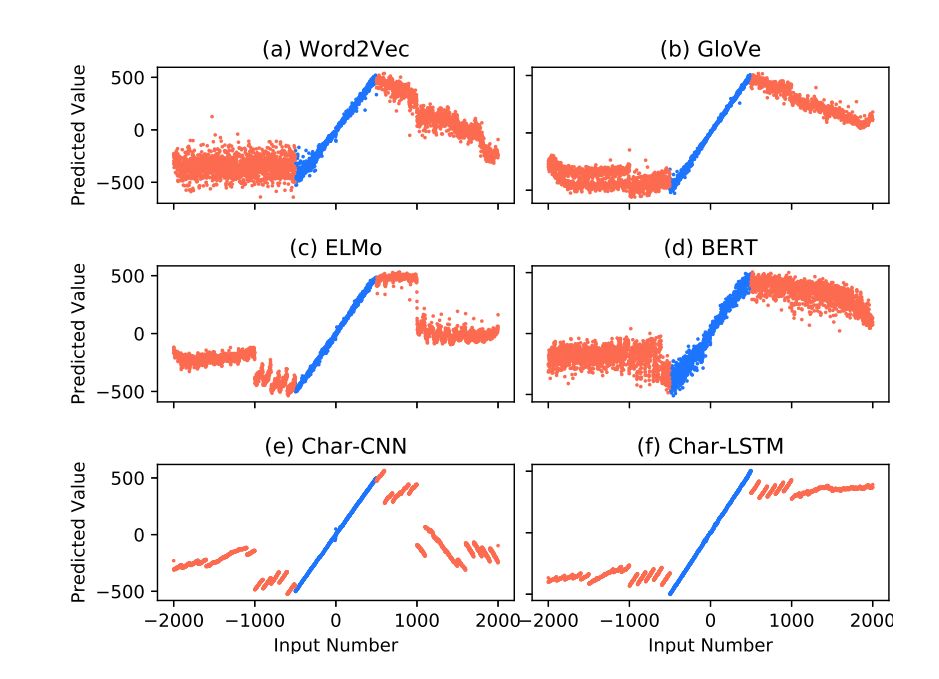
Decoding: Explore whether the size of numbers can be recognized.
Addition: This task requires numerical operations: given the embeddings of two numbers, the task is to predict their sum.

Researchers evaluated various token embedding methods:

Word vectors: Using 300-dimensional GloVe and word2vec vectors.
Contextual embeddings: Using ELMo and BERT embeddings.
NAQANet embeddings: Training the NAQANet model on the DROP dataset, extracting GloVe embeddings and Char-CNN.
Pre-trained embeddings: Using character-level CNN (Char-CNN) and character-level LSTM (Char-LSTM).
Embedding numbers as values: Directly mapping the embeddings of numbers to their values.

Results: The Numeracy Ability of Embeddings

Researchers found that all pre-trained embeddings contain fine-grained information about quantity and order. The researchers first explored integers (see Table 4):

Table 4:Interpolation using integers (such as 18).All pre-trained embedding methods (such as GloVe and ELMo) are capable of capturing numbers.The probing model was trained on 80% of randomly shuffled integers and tested on the remaining 20% of numbers.

Finally, researchers explored the embeddings of word form numbers, floating-point numbers, and negative numbers, finding that these inputs exhibit trends similar to integers: pre-trained models demonstrate natural mathematical understanding and learn strong embeddings (see Tables 5, 6, and 10).

Table 5:Interpolation using floating-point numbers (such as 18.1) in the list maximum task.Pre-trained embeddings recognize floating-point numbers.The probing model was trained on 80% of randomly shuffled integers and tested on the remaining 20% of numbers.

Can Embedded Vectors Understand Numbers? BERT vs. ELMo

Table 6:Interpolation using negative numbers (such as -18) in the list maximum task.Pre-trained embeddings recognize negative numbers.

Probing Model Struggles with Extrapolation

Previously, comprehensive experiments were typically evaluated on held-out values within the same range as the training data. However, now researchers trained models on specific integer ranges and tested them on ranges larger than the maximum training number and smaller than the minimum training number.

The accuracy of the list maximum task is close to that of the model in the interpolation environment. However, there remains a gap. Table 7 shows the accuracy of models trained on the integer range [0,150] and tested on ranges [151,160], [151,180], and [151,200], with all methods performing poorly, especially the token vectors.

Table 7:Extrapolation results on the list maximum task.The probing model was trained on the integer range [0,150] and evaluated on the integer ranges [151,160], [151,180], and [151,200].

This article is compiled by Machine Heart, for reprint, please contact this public account for authorization.

✄————————————————

Join Machine Heart (Full-time Journalist / Intern): [email protected]

Submissions or inquiries: content@jiqizhixin.com

Advertising & Business Cooperation: [email protected]

Leave a Comment Cancel reply