New Media Manager
Liú Shūlóng, currently an engineer in the technology department of Daguan Data, with interests primarily in natural language processing and data mining.
Word2vec is one of the achievements of the Google research team, and as a mainstream tool for obtaining distributed word vectors, it has a wide range of applications in natural language processing, data mining, and other fields. Some aspects of Daguan Data’s text mining business utilize this technology. This article briefly introduces the Word2vec skip-gram model from the following aspects:
The first part compares Word2vec word vectors with one-hot word vectors, highlighting the advantages of Word2vec word vectors; the second part provides related content about the skip-gram model; the third part briefly introduces optimization aspects during model solving; the fourth part gives examples of the effectiveness of word vector models; the fifth part concludes.
Advantages
Compared to traditional one-hot word vectors, Word2vec word vectors have the following two main advantages.
1. Low-Dimensional Dense
Generally, the dimensionality of distributed word vectors is set to 100-500, which is sufficient, while the dimensionality of one-hot type word vectors is proportional to the size of the vocabulary, making it a high-dimensional sparse representation method, which results in relatively low computational efficiency.
Fig.1. One-hot word vector
2. Semantic Information Containment
The one-hot representation makes each word orthogonal in high-dimensional space, meaning there are no relationships between words in the one-hot vector space, which is clearly inconsistent with reality, as words have various relationships such as synonyms and antonyms. Although Word2vec cannot learn high-level semantic information like antonyms, it cleverly employs the idea that “words with similar contexts contain similar meanings,” allowing semantically similar words to have high cosine similarity when mapped to Euclidean space.
Fig.2. Word2vec word vector
1. Training Samples
How to integrate the idea of “words with similar contexts contain similar meanings” into the model is a crucial step. In the model, whether two words appear together is determined by whether they appear within a context window. For example, the original sample “Daguan Data is a company engaged in artificial intelligence” will be processed as shown in Figure 3 (assuming a window size of 2 for simplicity; generally, the window is set to 5).
As shown in Figure 3, the input to the skip-gram model is the current word, and the output is the context of the current word. Although we train the model with pre-segmented sentences, internally it actually uses individual word pair for training. Similarly, for the previous case “Daguan Data is a company engaged in artificial intelligence,” if the window is changed to 5, the word pair (Daguan Data, artificial intelligence) will become a training sample.
If another case comes in, “Google is an artificial intelligence company,” then (Google, artificial intelligence) will also become a training sample. If multiple training samples of (Daguan Data, artificial intelligence) and (Google, artificial intelligence) are generated in the training corpus, it can be inferred that “Daguan Data” and “Google” will have a high similarity, because these two words have the same output in the training samples, implying that they have similar contexts. In short, “if two words have the same output, it can be inferred that the two input words have high similarity.” The next step is how to use the model to achieve this goal.
Fig.3. Training samples
2. Skip-Gram Model
The skip-gram model is similar to an autoencoder (Autoencoder), the only difference is that the output of the autoencoder equals the input, while the output of the skip-gram model is the context of the input. So, how should the training sample word pairs be input into the model? The answer is the one-hot vector. To obtain a one-hot vector, it is first necessary to know how many words are in the training corpus. Therefore, before training, the corpus is first counted to obtain the vocabulary. Assuming the vocabulary length is 10000 and the word vector is 300 dimensions, the skip-gram model can be represented as shown in Figure 4.
Fig.4. Skip-gram model
As shown in Figure 4, if the input word pair is (ants, able), the model fitting objective is to predict the context words for ants, and it must also satisfy the likelihood function represented as:
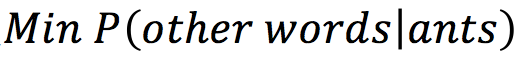while also satisfying the likelihood function represented as:
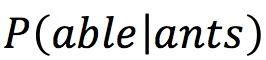where the log-likelihood function can be represented as:
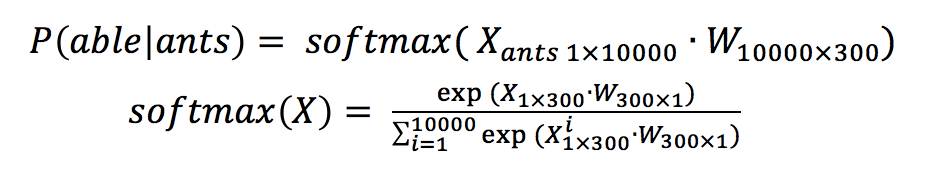
Based on the above, the likelihood function can be constructed:
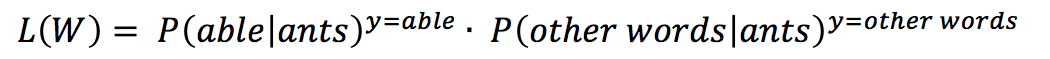
Then:
Substituting in the expression:
where {* indicates that if the expression* istrue, then{*}=1, otherwise{*}=0. The next step is to maximize the likelihood function, which is:
To achieve the above goal, gradient ascent can be utilized, first taking the partial derivative of the parameters:
Next, update the parameters based on the learning rate:
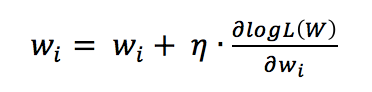
Now the question arises: where are the word vectors after the model training is complete? The hidden layer’s parameter matrix contains all the word vectors, where the rows represent the vocabulary length and the columns represent the word vector dimensions. Each row in the matrix represents a word’s word vector. Since the input layer is a one-hot vector, multiplying it with the hidden layer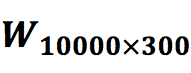 
effectively selects a row from that matrix, as shown in Figure 5, this row represents the word vector for ants, while the output layer uses the word vector for ants as features, training the softmax classifier with the context words of ants as categories.
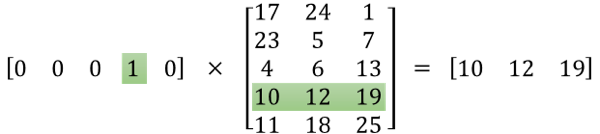
Fig.5. The word’s one-hot vector multiplied by the hidden layer’s weight matrix to obtain the word’s vector
Returning to the previous point, why do we say that after having multiple samples like (Daguan Data, artificial intelligence) and (Google, artificial intelligence), the similarity between Daguan Data and Google is likely to be high? The explanation was that these two words have the same output. To delve deeper, it is because the output layer’s parameter matrix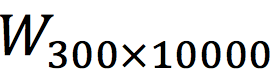 
is shared among all word vectors. Specifically, after the model training is complete, it will reach a state similar to the one shown below:
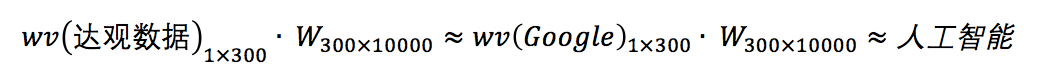
It can be directly seen from the above that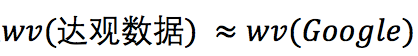 
represents the word vector of *, approximately indicating that the directions of the two vectors are close in space.
Model Optimization
1. Subsampling
In the example shown in Figure 3, words like “is” and “of” may appear in any context, and they do not contain much semantic meaning, yet they occur very frequently. If not processed, they can affect the quality of word vectors. Subsampling is aimed at addressing this phenomenon, where the main idea is to calculate a sampling probability for each word and determine whether a word should be retained based on its probability. The probability calculation method is:
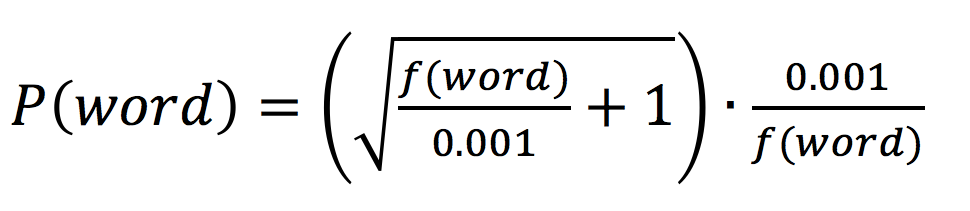
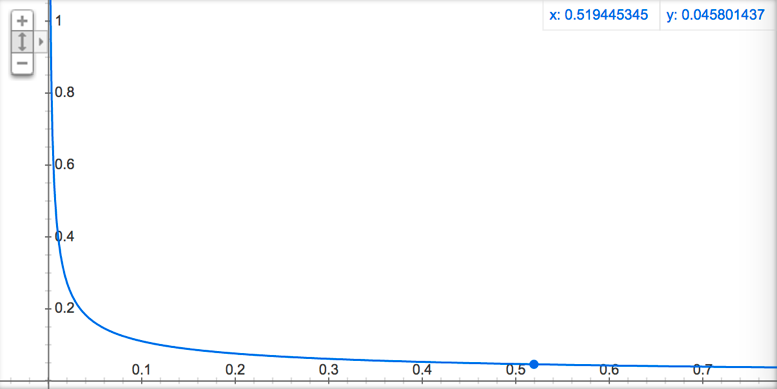
where f(*) represents the probability of * occurring, 0.001 is the default value, and the specific function curve is shown in Figure 6. It can be seen that the higher the probability of a word occurring, the lower its sampling probability. This has a flavor of IDF, except that IDF is used to reduce the feature weight of words, while subsampling is to reduce the sampling probability of words.
2. Negative Sampling
Taking the model shown in Figure 4 as an example, for each training sample, the number of parameters that need to be updated is three million (to be precise, three million and three hundred; since the input is one-hot, the hidden layer only needs to update the word vector of the input word). This is still assuming that the vocabulary has only ten thousand words; in reality, it could have five hundred thousand or even more, reaching billions of parameters. During training, the model needs to calculate the partial derivative for each parameter and then update it, which requires significant computational resources.
Negative sampling is a method to speed up training, where the term negative can be understood as negative samples. For the training sample (ants, able), able is the positive sample, while all words in the vocabulary except able are negative samples. Negative sampling focuses on sampling from the negative samples; without negative sampling, for each training sample, the model needs to fit one positive sample and nine thousand nine hundred ninety-nine negative samples. With negative sampling, only a few negative samples need to be selected from those nine thousand nine hundred ninety-nine for fitting, greatly saving computational resources. How many negative samples should be selected, and based on what criteria? Google suggests selecting 5-20 samples, and the selection is based on the probability of the word appearing in the corpus; the higher the probability, the more likely it is to be selected, with the specific calculation formula being:
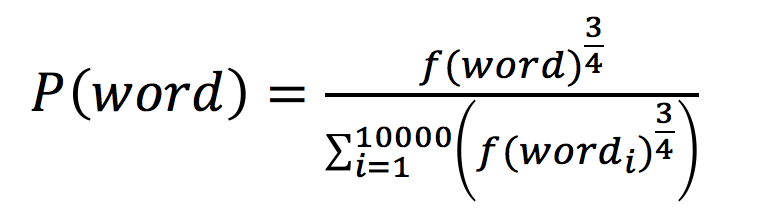
where f(*) represents the probability of * occurring.
3. Hierarchical Softmax
The purpose of hierarchical softmax is the same as that of negative sampling, which is to speed up training, but it is relatively more complex and not as straightforward as negative sampling. Specifically, when using hierarchical softmax, the output layer of the model shown in Figure 4 no longer uses one-hot plus softmax regression, but uses a Huffman tree plus softmax regression. During model training, the frequency of words in the corpus is first counted, and a Huffman tree is constructed based on word frequency, as shown in Figure 7. The root node of the tree can be understood as the word vector of the input word, while the leaf nodes represent the words in the vocabulary; other nodes have no practical significance and serve only as auxiliary roles.
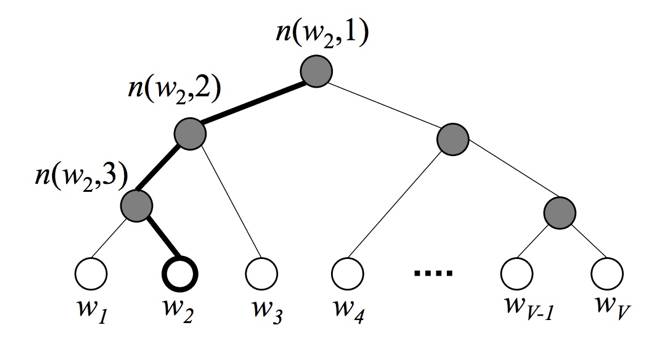
Fig.7. Huffman Tree
Why does using a Huffman tree speed up training? The answer is that the output layer does not use one-hot representation, meaning softmax regression does not need to fit so many 0s (i.e., negative samples); it only needs to fit the output values along one path in the Huffman tree. Assuming the vocabulary size is N, the number of nodes along one path can be estimated, meaning it only needs to fit O(log(N)) times, which results in an exponential reduction in computational load. Additionally, since Huffman coding is variable-length coding, words with higher frequencies are closer to the root node, which also reduces the computational load.
How to fit the nodes in the tree? As shown in Figure 7, if the output word for the training sample is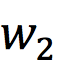 
, then moving from the root node to 
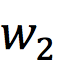passes through these two nodes. Since the Huffman tree is a binary tree, it only requires determining whether to go left or right to reach 
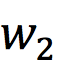. Determining left or right essentially means performing binary classification. In the example in Figure 7, “root(input)->left->left->right()” can be represented as:
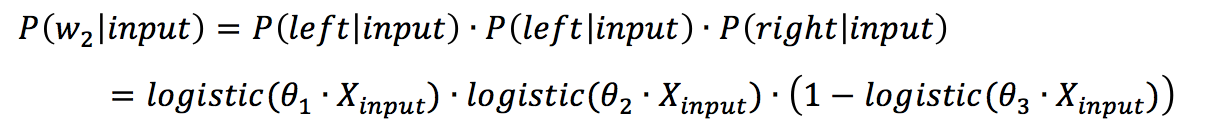
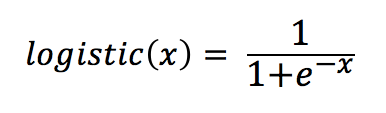
where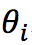 
represents the weight vector of the ith node in the path. Note that softmax regression degenerates to logistic regression when performing binary classification, so although it’s called hierarchical softmax, the formula actually uses the logistic function. Based on the above formula, a cost function for softmax regression based on the Huffman tree can be constructed, which can then be used to train and solve the model through gradient descent.
Google has open-sourced the word2vec source code, making it easy to train word vectors; this will not be elaborated here. A brief example:
It can be seen that when the input is the word Beijing, the similar words are “Shanghai, Guangzhou, Hangzhou, Shenzhen…”, indicating that the model has almost learned the concept of first-tier cities, which is quite effective.
1. Daguan Application Case
Feature Dimensionality Reduction: When the feature dimensions are too high, it is easy for features to have high correlations. In this case, word vector tools can be used for clustering features, consolidating related features into one dimension.
Feature Expansion: When processing short texts, a case often fails to produce many strong meaning features, leading to weak distinctions between categories. In this case, word vector tools can be used to expand the main features, improving recall without losing accuracy.
This article briefly introduced the skip-gram model of Word2vec from examples, serving merely as a starting point. If there are any inaccuracies in the text, corrections are welcome.
Click “Read More” or “Long Press the QR Code Below” to apply for a trial of Daguan products.
