XGBoost Hyperparameter Tuning Guide

XGBoost Hyperparameter Tuning Guide

by

Source: DeepHub IMBA

This article will detail the introduction, function, and value range of the ten most commonly used hyperparameters in XGBoost, as well as how to use Optuna for hyperparameter tuning.

The default hyperparameters for XGBoost work fine, but if you want to achieve the best results, you need to adjust some hyperparameters to match your data. The following parameters are very important for XGBoost:

  • eta

  • num_boost_round

  • max_depth

  • subsample

  • colsample_bytree

  • gamma

  • min_child_weight

  • lambda

  • alpha

XGBoost has two API calling methods: the native API we commonly see, and the API that is compatible with Scikit-learn, which integrates seamlessly with the Sklearn ecosystem. Here we will focus on the native API (which is the most common), but here is a list to help you compare the parameters of the two APIs, just in case you need it in the future:

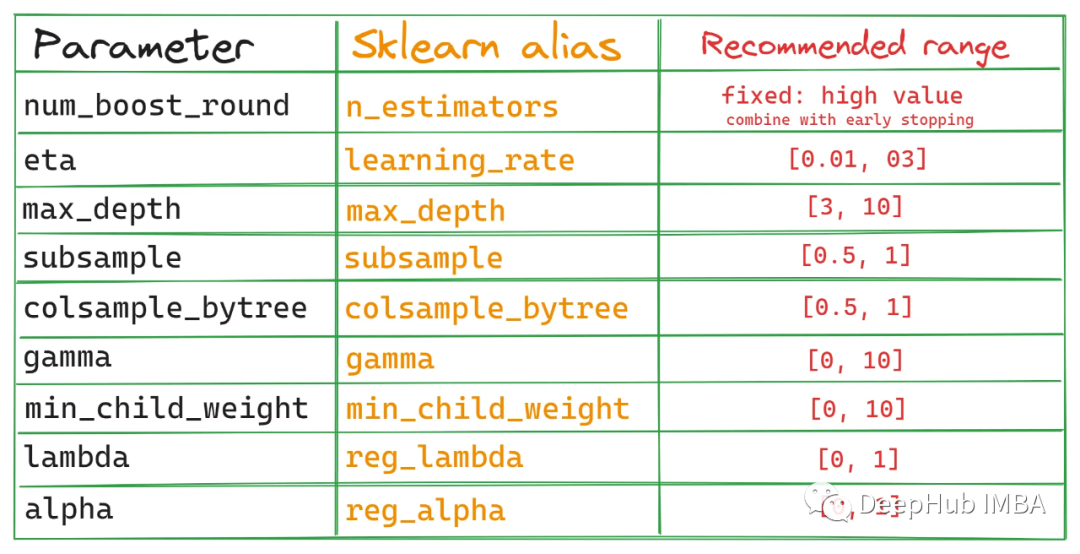
XGBoost Hyperparameter Tuning Guide

If you want to use hyperparameter tuning tools other than Optuna, you can refer to this table. The following image shows the interactions between these parameters:

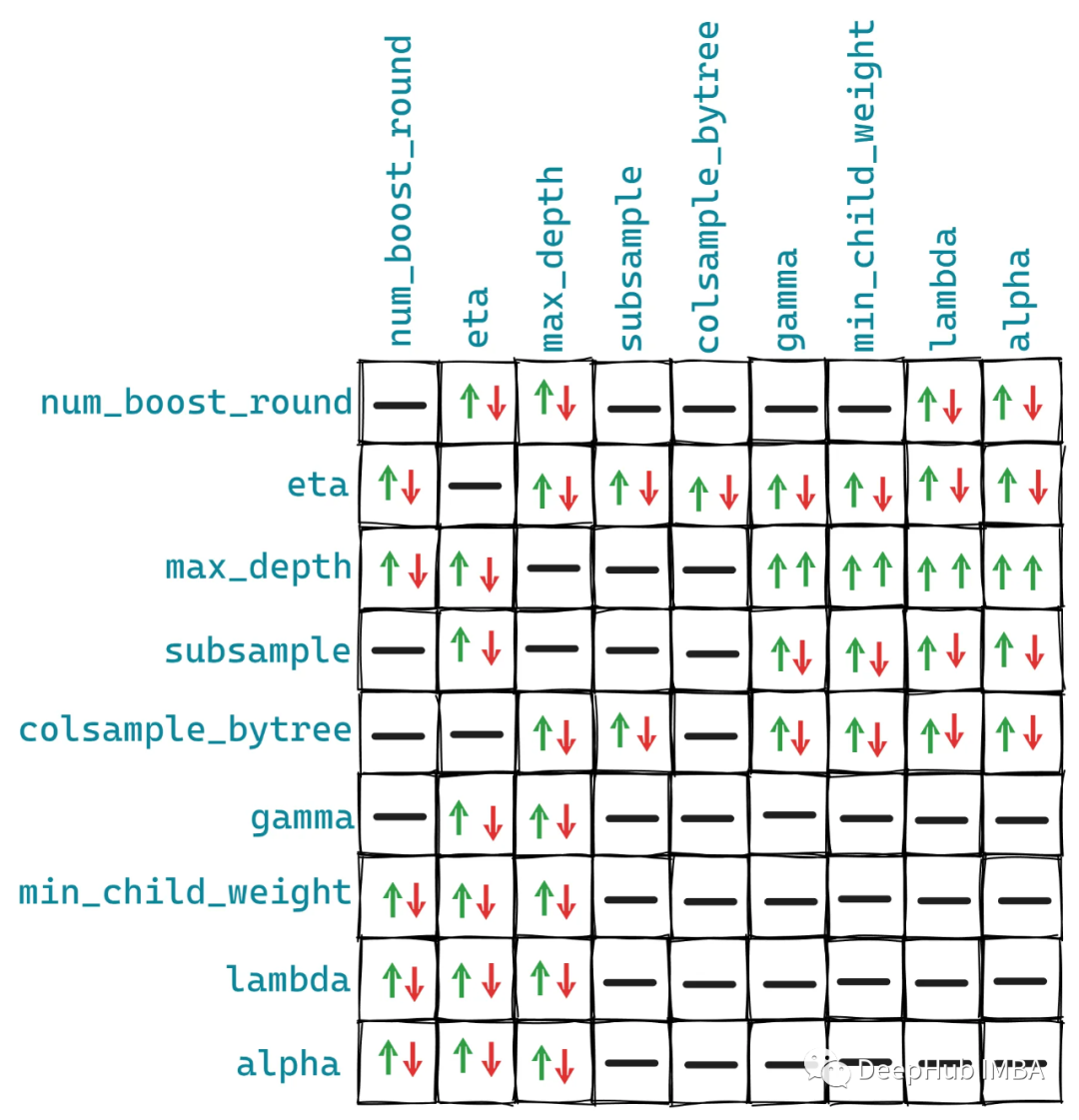
XGBoost Hyperparameter Tuning Guide

These relationships are not fixed, but the general situation is as shown in the image above, because some other parameters may have additional effects on our ten parameters.

1. objective

This is the training objective of our model.

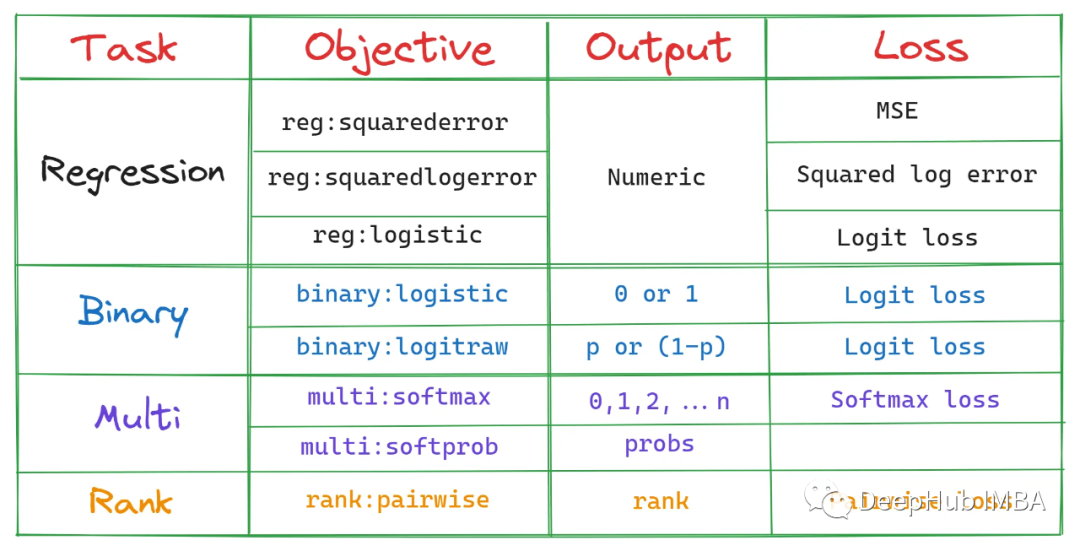
XGBoost Hyperparameter Tuning Guide

The simplest explanation is that this parameter specifies what we want our model to do, which affects the type of decision tree and the loss function.

2. num_boost_round

num_boost_round specifies the number of decision trees (usually referred to as base learners in XGBoost) to be generated during training. The default value is 100, but this is far from enough for today’s large datasets.

Increasing this parameter can generate more trees, but as the model becomes more complex, the chances of overfitting will also significantly increase.

A tip learned from Kaggle is to set a high value for num_boost_round, such as 100,000, and use early stopping to obtain the best version.

In each boosting round, XGBoost generates more decision trees to improve the overall score of the previous decision tree. That’s why it’s called boosting. This process continues until the num_boost_round polling is completed, regardless of whether there is an improvement compared to the previous round.

However, by using the early stopping technique, we can stop training when the validation metric does not improve, saving time and preventing overfitting.

With this tip, we don’t even need to tune num_boost_round. Here is how it looks in code:

# Define the rest of the params params = {...} # Build the train/validation sets dtrain_final = xgb.DMatrix(X_train, label=y_train) dvalid_final = xgb.DMatrix(X_valid, label=y_valid) bst_final = xgb.train(    params,    dtrain_final,    num_boost_round=100000, # Set a high number    evals=[(dvalid_final, "validation")],    early_stopping_rounds=50, # Enable early stopping    verbose_eval=False, )

The code above makes XGBoost generate 100k decision trees, but since early stopping is used, it will stop when the validation score does not improve in the last 50 rounds. Generally, the number of trees ranges from 5000 to 10000. Controlling num_boost_round is also one of the biggest factors affecting the running time of the training process because more trees require more resources.

3. eta

This parameter is the learning rate (eta). In each round, all existing trees return a prediction for the given input. For example, five trees might return the following predictions for sample N:

Tree 1: 0.57   Tree 2: 0.9   Tree 3: 4.25   Tree 4: 6.4   Tree 5: 2.1

To return the final prediction, these outputs need to be aggregated, but before that, XGBoost uses a parameter called eta or learning rate to scale them down. The final output after scaling is:

output = eta * (0.57 + 0.9 + 4.25 + 6.4 + 2.1)

A large learning rate gives a greater weight to each tree’s contribution to the ensemble, but this can lead to overfitting/unsteadiness and speed up training time. A lower learning rate suppresses each tree’s contribution, making the learning process slower but more robust. This regularization effect of the learning rate parameter is particularly useful for complex and noisy datasets.

The learning rate is inversely related to other parameters such as num_boost_round, max_depth, subsample, and colsample_bytree. A lower learning rate requires higher values for these parameters, and vice versa. However, generally, there is no need to worry about the interactions between these parameters because we will use automated tuning to find the best combination.

4. subsample and colsample_bytree

Subsample introduces more randomness into the training, helping to combat overfitting.

Subsample = 0.7 means that each decision tree in the ensemble will be trained on a randomly selected 70% of the available data. A value of 1.0 means that all rows will be used (no subsampling).

Similar to subsample, there is also colsample_bytree. As the name suggests, colsample_bytree controls the proportion of features that each decision tree will use. Colsample_bytree = 0.8 means that each tree uses 80% of the available features (columns) randomly.

Tuning these two parameters can control the trade-off between bias and variance. Using smaller values reduces the correlation between trees, increases diversity in the ensemble, and helps improve generalization and reduce overfitting.

However, they may introduce more noise and increase the model’s bias. Using larger values increases the correlation between trees, decreases diversity, and may lead to overfitting.

5. max_depth

max_depth controls the maximum number of layers that a decision tree can reach during training.

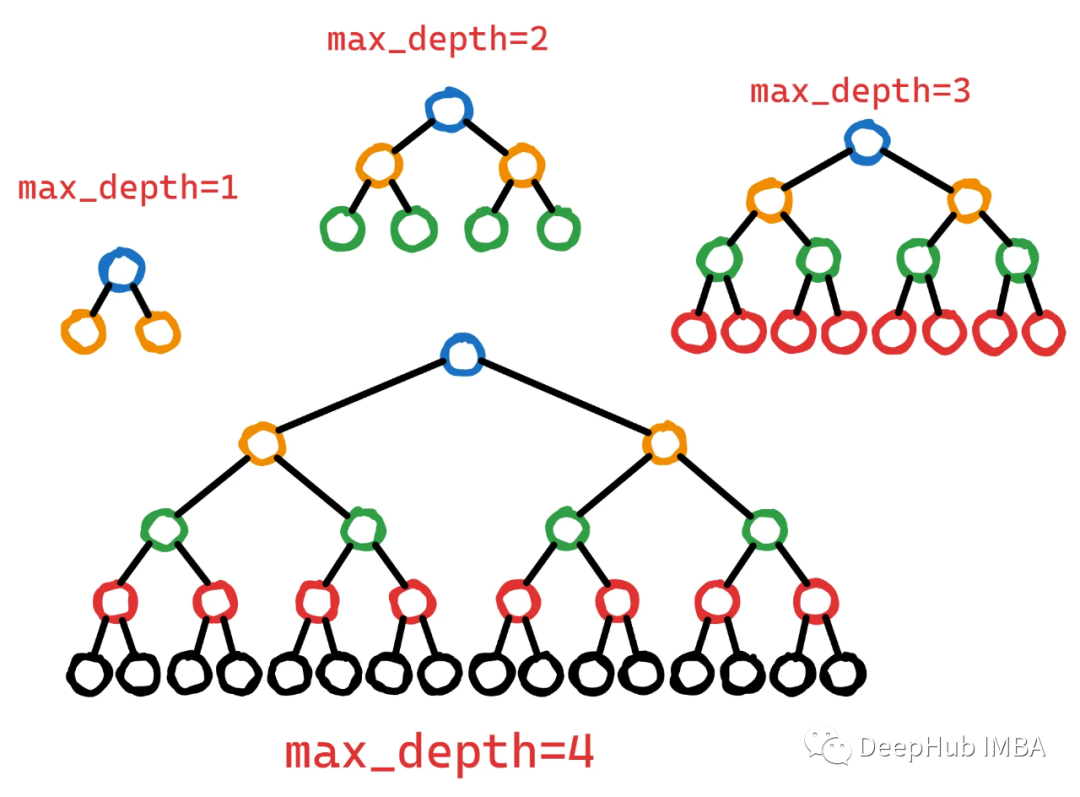
XGBoost Hyperparameter Tuning Guide

Deeper trees can capture more complex interactions between features. However, deeper trees also have a higher risk of overfitting because they can memorize noise or irrelevant patterns in the training data. To control this complexity, max_depth can be limited to generate shallower, simpler trees that capture more general patterns.

The value of max_depth can balance complexity and generalization well.

6, 7. alpha, lambda

These two parameters are discussed together because alpha (L1) and lambda (L2) are two regularization parameters that help prevent overfitting.

Unlike other regularization parameters, they can shrink the weights of unimportant or irrelevant features to 0 (especially alpha), resulting in a model with fewer features and reduced complexity.

The effects of alpha and lambda may be influenced by other parameters such as max_depth, subsample, and colsample_bytree. Higher values of alpha or lambda may require adjustments to other parameters to compensate for the increased regularization. For example, a higher alpha value may benefit from a larger subsample value as this can maintain model diversity and prevent underfitting.

8. gamma

If you have read the XGBoost documentation, it states that gamma is:

The minimum loss reduction required to make a further partition on a leaf node of the tree.

I feel that other than the person who wrote this sentence, no one else can understand it. Let’s see what it really is; here is a two-layer decision tree:

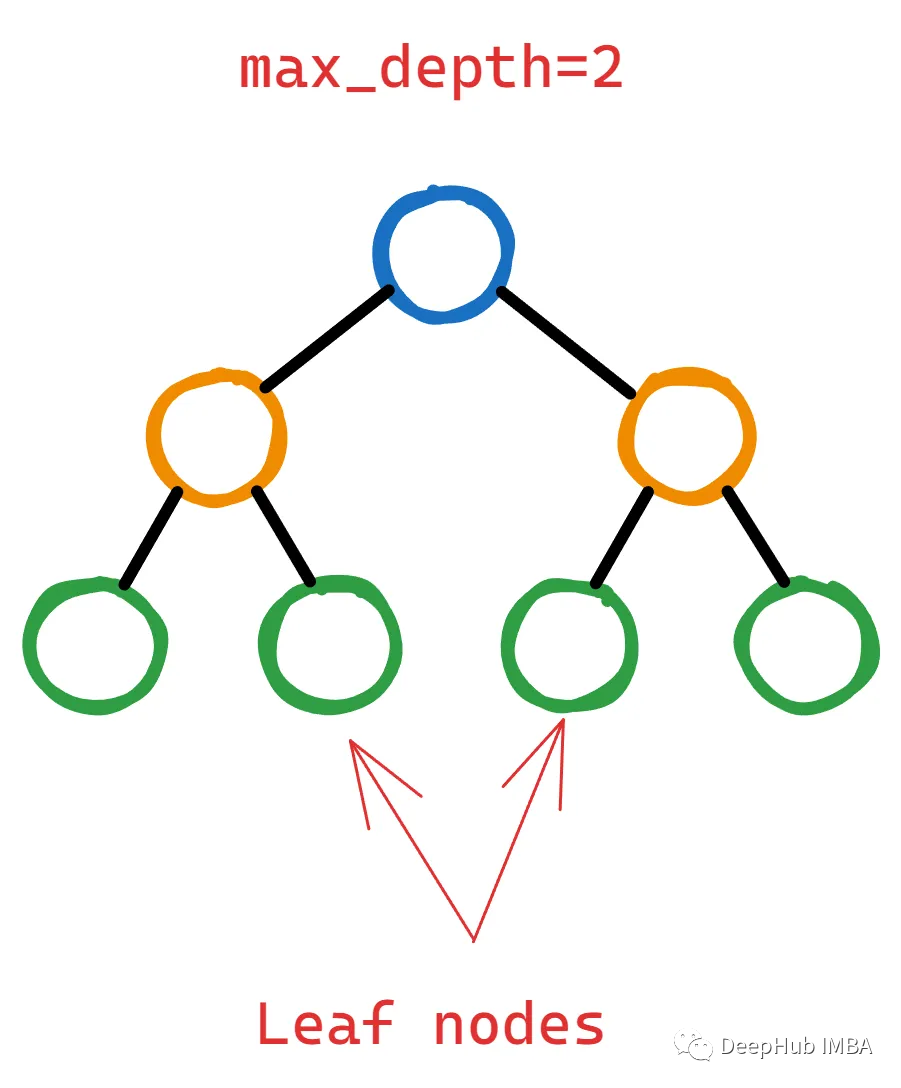
XGBoost Hyperparameter Tuning Guide

To justify adding more layers to the tree by splitting leaf nodes, XGBoost must calculate whether this operation can significantly reduce the loss function.

But “how significant is significant?” That’s gamma—it acts as a threshold to decide whether a leaf node should be further split.

If the reduction in the loss function (often referred to as gain) after a potential split is less than the chosen gamma, the split is not performed. This means the leaf node remains unchanged, and the tree will not grow from that point.

So the tuning goal is to find the best split that leads to the maximum reduction in the loss function, which means improved model performance.

9. min_child_weight

XGBoost starts its initial training process with a single decision tree that has a single root node. This node contains all training instances (rows). As XGBoost selects potential features and splitting criteria to minimize loss, deeper nodes will contain fewer and fewer instances.

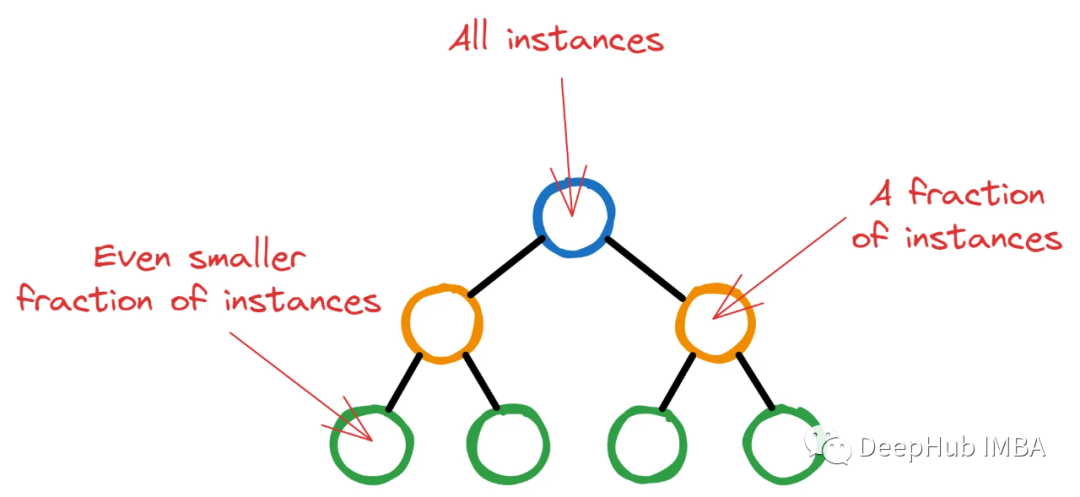
XGBoost Hyperparameter Tuning Guide

If XGBoost runs arbitrarily, the tree may grow to the point where there are only a few irrelevant instances in the last node. This situation is highly undesirable because it is the very definition of overfitting.

Therefore, XGBoost sets a threshold for the minimum number of instances in each node for further splitting. By weighting all instances in the node and finding the total weight, if this final weight is less than min_child_weight, the split stops, and the node becomes a leaf node.

The explanation above is a simplified version of the entire process, as we mainly introduce its concept.

This concludes our explanation of these 10 important hyperparameters.

Recommended Reading

👉 Advanced Pandas Guide

👉 Data Mining Practical Projects

👉 Introduction to Machine Learning

Leave a Comment