XGBoost is an excellent algorithm that has been widely used in many competitions such as Kaggle, where we can see that many winning teams utilize XGBoost and achieve outstanding performance. Currently, most classification models in practical applications are based on XGBoost, making it a very practical and user-friendly algorithm. The main reference for this article is the paper by its inventor, Tianqi Chen, available at https://arxiv.org/abs/1603.02754. It is worth mentioning that the inventor is Chinese and was trained in the ACM system at Shanghai Jiao Tong University. Not only did he invent the XGBoost algorithm, but he also open-sourced it, which is truly admirable.
XGBoost shares the same roots with the boosting tree algorithms discussed previously (otherwise, it wouldn’t have the term ‘boost’ in its name). Its main idea is that the overall model is the sum of a series of models.
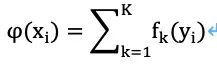
In each iteration, XGBoost builds on the previous model and introduces a new model fk. This means that after each iteration, the overall model φ improves its performance by incorporating the new model fk. Ultimately, multiple learners are combined for the final prediction, resulting in higher accuracy than a single model. This is fundamentally no different from the boosting algorithm.
For a regression problem, its training dataset is T={(x1, y1), (x2, y2), … (xN, yN)}. The features are n-dimensional real vectors xi ∈ Rn, and the outputs are yi ∈ R. The idea of an ensemble tree model is to use K accumulated basic discriminative functions to predict the output, which means the model’s output value:
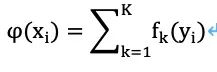
Basic Discriminative Function – CART
The basic discriminative function fk is the regression tree CART we discussed earlier. It takes an m-dimensional real vector as input and partitions the input space into T units R1, R2, …, RT based on the characteristics of these real vectors, with a fixed output value wi in each unit Ri. When the input x falls into that space unit, it outputs a specific weight. This is how a regression tree with T leaf nodes operates (of course, the tree may have levels in between; this is a simplified illustration).
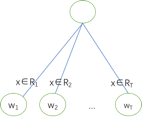
Thus, a discriminative function, that is, a regression tree, can be represented using the tree structure q (which represents the partitioning of the input space) and the weight vector w (which represents the output results for each input space).
This algorithm framework is called the Tree Ensemble Model, as exemplified in the paper. For instance, consider a specific person’s preference for a certain computer game. This can be assessed using two trees, which are then combined. The first tree considers age and gender, while the second tree considers the frequency of computer use.
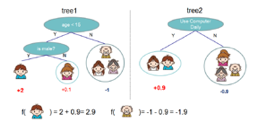
The final output is the sum of the scores from the two trees. The young boy scores 2 in the first tree and 0.9 in the second tree, resulting in a total output of 2.9; the old man scores -1 – 0.9 = -1.9.
