Understanding XGBoost and LightGBM: Mainstream Ensemble Algorithms

Click the “Datawhalee” above and select “star” in the official account

Get valuable content instantly

This is the third article on decision trees, mainly introducing mainstream ensemble algorithms based on the Boosting framework, including XGBoost and LightGBM.

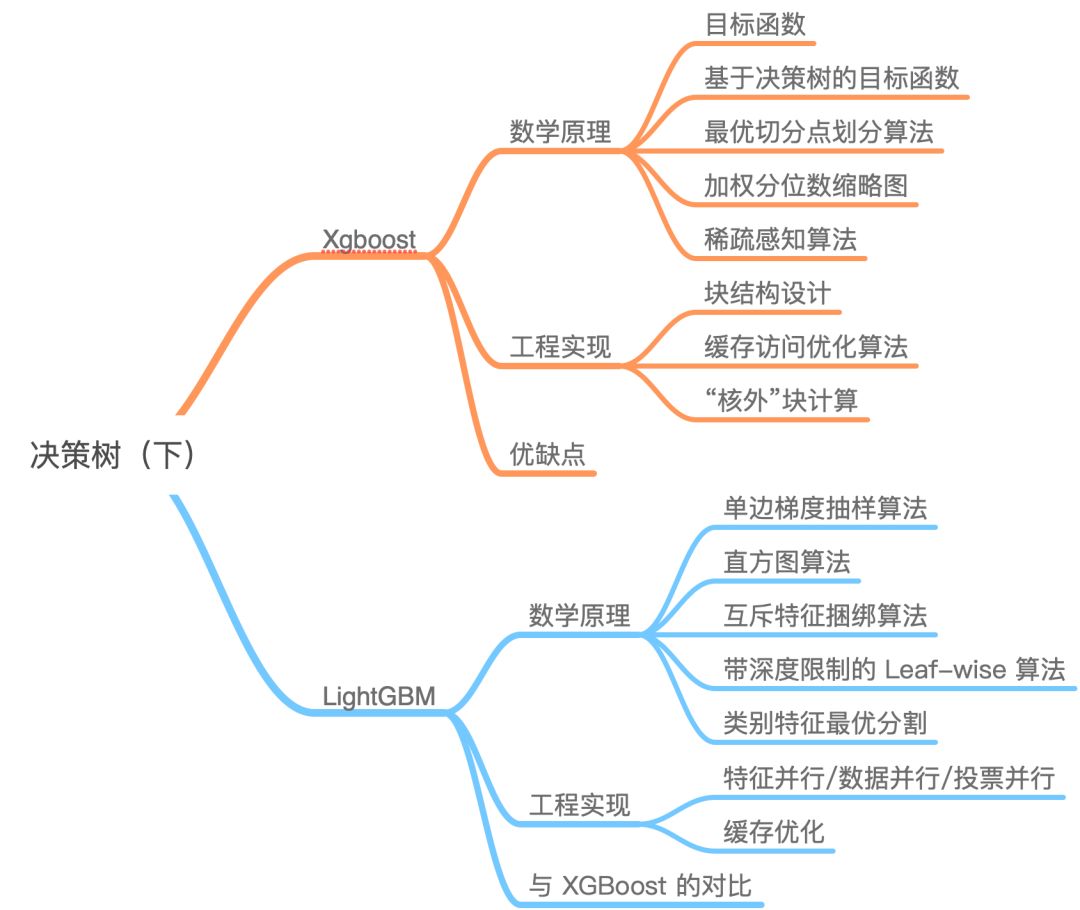
Here is the complete mind map:

XGBoost

XGBoost is a tool for large-scale parallel boosting trees. It is currently the fastest and best open-source boosting tree toolkit, over 10 times faster than common toolkits. Both Xgboost and GBDT are boosting methods; aside from differences in engineering implementation and problem-solving, the biggest difference lies in the definition of the objective function. Therefore, this article will introduce the mathematical principles and engineering implementations, and finally discuss the advantages of Xgboost.1.1 Mathematical Principles1.1.1 Objective FunctionWe know that XGBoost is an additive expression composed of k base models: where is the k-th base model, and is the predicted value for the i-th sample.The loss function can be represented by the predicted value and the true value : where n is the number of samples.We know that the model’s prediction accuracy is determined by the model’s bias and variance, and the loss function represents the model’s bias. To achieve low variance, a simple model is needed, so the objective function is composed of the model’s loss function L and a regularization term that suppresses model complexity, thus we have: is the model’s regularization term. Since XGBoost supports both decision trees and linear models, we will not elaborate on it here.We know that boosting models are forward additive. Taking the model at step t as an example, the model’s prediction for the i-th sample is: where is the prediction value given by the model at step t-1, which is a known constant, and is the prediction value of the new model we need to add this time. At this point, the objective function can be written as:To optimize the objective function at this time is equivalent to solving .The Taylor formula is a method to approximate a function f(x) that has an n-th derivative at a point using an n-th polynomial in terms of . If the function f(x) has an n-th derivative in a closed interval that includes , and has an (n+1)-th derivative in the open interval (a,b), then for any point x in the closed interval, we have where the polynomial is called the Taylor expansion of the function at . is the remainder of the Taylor formula and is a higher-order infinitesimal of .According to the Taylor formula, we can perform a second-order Taylor expansion of the function at point x to obtain the following equation:We treat as and as , so we can write the objective function as: where is the first derivative of the loss function, and is the second derivative of the loss function. Note that the derivative here is taken with respect to .Taking the squared loss function as an example: then:Since at step t, is actually a known value, thus is a constant, and its optimization will not affect the function, therefore the objective function can be written as:Thus, we only need to find the first and second derivatives of the loss function at each step (since the previous step’s is known, these two values are constants), and then optimize the objective function to get each step’s f(x). Finally, using the additive model, we can obtain an overall model.1.1.2 Objective Function Based on Decision TreesWe know that Xgboost’s base model supports not only decision trees but also linear models. Here we mainly introduce the objective function based on decision trees.We can define a decision tree as , where x is a certain sample, and q(x) represents which leaf node the sample is in, while w_q represents the value of the leaf node w, so represents the value w (i.e., predicted value) for each sample.The complexity of the decision tree can be represented by the number of leaves T; the fewer leaf nodes, the simpler the model. Additionally, leaf nodes should not have excessively high weights w (similar to the weight of each variable in LR), so the regularization term of the objective function can be defined as: that is, the complexity of the decision tree model is jointly determined by the number of leaf nodes of all generated decision trees and the vector composed of the weights of all nodes.

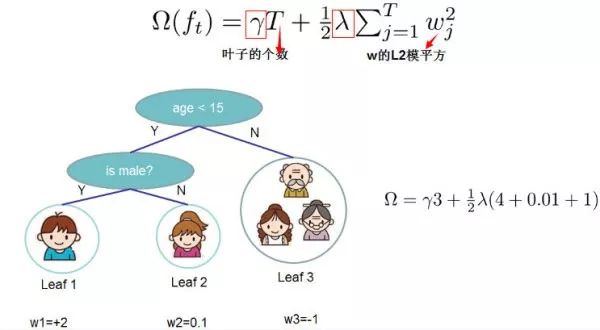
This image shows the method for solving the regularization term of XGBoost based on decision trees.We set as the sample set of the j-th leaf node, thus our objective function can be written as:The second step to the third step may not be very clear, so let me explain:The second step is to traverse all samples to calculate the loss function for each sample, but samples will eventually fall into leaf nodes, so we can also traverse leaf nodes and then obtain the sample set on the leaf nodes, and finally calculate the loss function.That is, the previous sample set is now rewritten as the leaf node set. Since a leaf node can contain multiple samples, this is why we have and two items, where is the value of the j-th leaf node.To simplify the expression, we define , then the objective function becomes:Here we must note that and are results obtained from the previous t-1 steps, their values are known and can be treated as constants, only the weight of the leaf node of the last tree is uncertain. Therefore, if we take the first derivative of the objective function with respect to and set it to 0, we can find the weight corresponding to the leaf node j:Thus, the objective function can be simplified to:

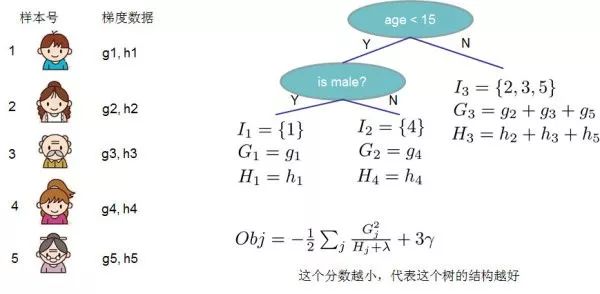
The above figure provides an example of calculating the objective function by finding the first derivatives and second derivatives for each node and each sample, and then summing and for each node based on the samples contained, finally traversing the nodes of the decision tree to obtain the objective function.1.1.3 Optimal Split Point AlgorithmIn the process of growing decision trees, a very critical issue is how to find the optimal split point for the leaf nodes. Xgboost supports two methods for splitting nodes: greedy algorithm and approximate algorithm.1) Greedy Algorithm

1. Start from a tree of depth 0, enumerate all available features for each leaf node;
2. For each feature, sort the training samples belonging to that node in ascending order based on the feature value, and determine the best split point for that feature through linear scanning, recording the split gain for that feature;
3. Select the feature with the highest gain as the splitting feature, using the best split point of that feature as the split position, splitting into two new leaf nodes and associating the corresponding sample set with each new node;
4. Return to step 1, recursively execute until specific conditions are met.

So how do we calculate the split gain for each feature?Assuming we complete feature splitting at a certain node, the objective function before splitting can be written as:The objective function after splitting is:Thus, for the objective function, the gain after splitting is:Note that the gain of that feature can also be an important basis for outputting feature importance.For each split, we need to enumerate all possible splitting schemes for features. How can we efficiently enumerate all splits?I assume we want to enumerate all conditions like x < a; for a specific split point a, we need to calculate the sum of the derivatives on the left and right of a.

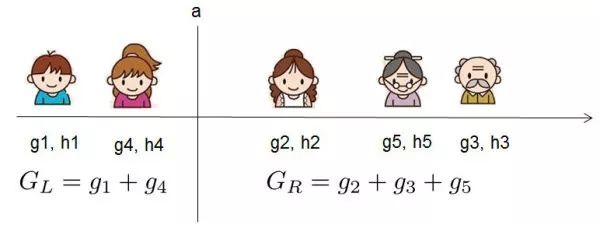
We can see that for all split points a, we only need to perform a left-to-right scan to enumerate all gradient sums and .Then use the above formula to calculate the score of each splitting scheme.2) Approximate AlgorithmThe greedy algorithm can obtain the optimal solution, but when the data volume is too large, it cannot be loaded into memory for computation. The approximate algorithm mainly provides an approximate optimal solution to address the shortcomings of the greedy algorithm.For each feature, only examining quantile points can reduce computational complexity.This algorithm will first propose candidate split points based on quantiles of the feature distribution, then map continuous features into buckets divided by these candidate points, and then aggregate statistical information to find the best split point for all intervals.When proposing candidate split points, there are two strategies:

• Global:Propose candidate split points before learning each tree and use this split in each split;
• Local:Re-propose candidate split points before each split.

Intuitively, the Local strategy requires more computational steps, while the Global strategy requires more candidate points because there are no splits in the nodes.The following figure shows the AUC transformation curves of different split strategies, where the x-axis is the number of iterations and the y-axis is the test set AUC, eps is the accuracy of the approximate algorithm, and its reciprocal is the number of buckets.

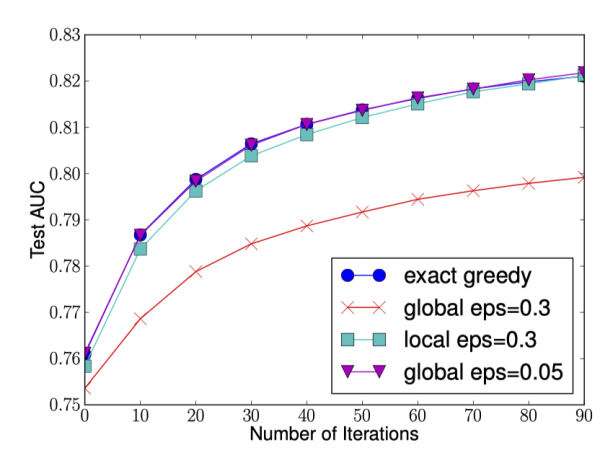
We can see that the Global strategy can achieve similar accuracy to the Local strategy when the number of candidate points is large (small eps) and the number of candidate points is small (large eps).Moreover, we also find that under reasonable eps values, the quantile strategy can achieve the same accuracy as the greedy algorithm.

• The first for loop:Find the candidate set of cutting points for feature k based on the distribution of that feature.XGBoost supports both Global and Local strategies.
• The second for loop:For the candidate set of each feature, map the samples into the bucket intervals formed by the candidate points corresponding to that feature, i.e., , and statistics G,H values for each bucket, finally finding the best split point based on these statistics.

The following figure provides a specific example of the approximate algorithm, taking the third quantile as an example:

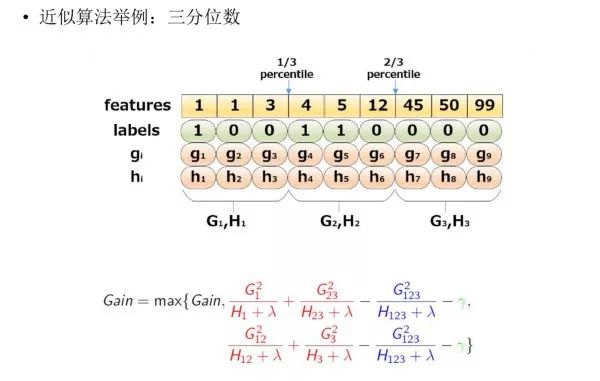
Sort the sample features, then divide based on quantiles, and count G,H values within the three buckets, ultimately solving for the gain of node partitioning.1.1.4 Weighted Quantile SketchIn fact, XGBoost does not simply divide quantiles based on the number of samples, but uses the second derivative value as the weight of the samples for partitioning, as shown below:

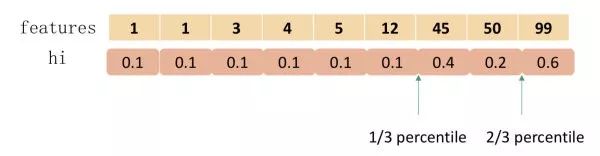
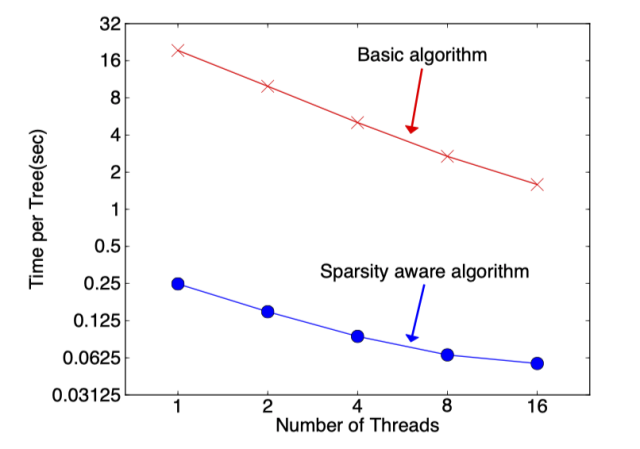
Then the question arises:Why use for sample weighting?We know that the model’s objective function is:With a little rearrangement, we can see that has a weighting effect on loss.Where and C are constants.We can see that h_i is the weight of the samples in the squared loss function.For datasets with equal sample weights, there is already a solution for finding candidate quantile points (the GK algorithm), but when the sample weights are different, how do we find candidate quantile points?(The author proposes a Weighted Quantile Sketch algorithm, which will not be introduced here.)1.1.5 Sparse-Aware AlgorithmIn the first article on decision trees, we introduced the splitting strategy of CART trees when dealing with missing data, and XGBoost also provides its solution.XGBoost only considers non-missing values in the process of building tree nodes, while adding a default direction for each node. When the corresponding feature value of the sample is missing, it can be classified into the default direction. The optimal default direction can be learned from the data.As for how to learn the default value’s branch, it’s quite simple; enumerate the gains when the feature is missing for the sample for both left and right branches, and choose the one with the highest gain as the optimal default direction.In the process of building the tree, it is necessary to enumerate the samples with missing features. At first glance, this algorithm seems to double the computation, but in fact, the algorithm only considers traversing samples with non-missing features, while samples with missing feature values do not need to traverse but can be directly assigned to the left and right nodes. Thus, the number of samples that the algorithm needs to traverse decreases, as can be seen in the figure below, the sparse-aware algorithm is over 50 times faster than the basic algorithm.

1.2 Engineering Implementation1.2.1 Block Structure DesignWe know that the most time-consuming step in learning decision trees is that each time the best split point is found, the feature values need to be sorted.And XGBoost sorts the data based on features before training and saves it into a block structure, using a sparse matrix storage format (Compressed Sparse Columns Format, CSC) in each block structure. The subsequent training process will repeatedly use the block structure, which can greatly reduce computational load.

• Each block structure includes one or more sorted features;
• Missing feature values will not be sorted;
• Each feature will store an index pointing to the sample gradient statistic values, facilitating the calculation of first and second derivative values;

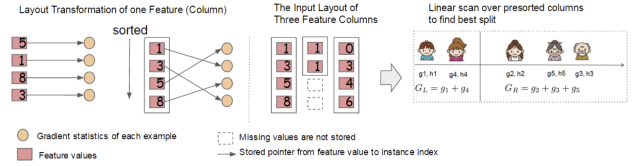
This block structure storage makes features independent of each other, facilitating parallel computation by computers.When splitting nodes, the feature with the highest gain needs to be selected as the split; thus, the gain calculations of each feature can be performed simultaneously, which is also the reason Xgboost can achieve distributed or multithreaded computation.1.2.2 Cache Access Optimization AlgorithmThe design of block structures can reduce the computational load during node splitting, but the design of accessing sample gradient statistics through index may lead to non-contiguous memory space access, which can result in low cache hit rates, thus affecting the efficiency of the algorithm.To solve the problem of low cache hit rates, XGBoost proposed a cache access optimization algorithm:Allocate a continuous cache area for each thread, storing the required gradient information in the buffer, thus achieving the conversion from non-contiguous space to contiguous space, improving algorithm efficiency.Additionally, appropriately adjusting the block size can also help optimize the cache.1.2.3 Out-of-Core Block ComputationWhen the data volume is too large to load all data into memory, it can only temporarily store data that cannot be loaded into memory on the hard disk and load it for computation when needed. However, this operation inevitably involves resource waste and performance bottlenecks due to differences in speed between memory and hard disk.To solve this problem, XGBoost has a dedicated thread for reading data from the hard disk, allowing data processing and data loading to occur simultaneously.Additionally, XGBoost employs two methods to reduce the overhead of hard disk read and write:

• Block Compression:Compress blocks by column and decompress them during reading;
• Block Splitting:Store each block on different disks, reading from multiple disks can increase throughput.

1.3 Advantages and Disadvantages1.3.1 Advantages

1. Higher accuracy:GBDT only uses first-order Taylor expansion, while XGBoost performs second-order Taylor expansion on the loss function.XGBoost introduces second derivatives to increase accuracy and to allow for custom loss functions; second-order Taylor expansion can approximate a large number of loss functions;
2. Greater flexibility:GBDT uses CART as the base classifier, while XGBoost supports both CART and linear classifiers (using a linear classifier in XGBoost is equivalent to logistic regression (classification problem) or linear regression (regression problem) with L1 and L2 regularization terms).Additionally, the XGBoost tool supports custom loss functions, as long as the function supports first and second derivatives;
3. Regularization:XGBoost incorporates regularization terms in the objective function to control model complexity.The regularization term includes the number of leaf nodes in the tree and the L2 norm of the leaf node weights.The regularization term reduces the variance of the model, making the learned model simpler and helping to prevent overfitting;
4. Shrinkage:Equivalent to learning rate.After each iteration, XGBoost multiplies the weights of the leaf nodes by this coefficient, mainly to weaken the influence of each tree, allowing for greater learning space later on;
5. Column sampling:XGBoost borrows from the random forest approach, supporting column sampling, which can reduce overfitting and computational load;
6. Handling missing values:The sparse-aware algorithm used by XGBoost greatly speeds up the node splitting process;
7. Can be parallelized:Block structures can effectively support parallel computation.

1.3.2 Disadvantages

1. Although using pre-sorting and approximate algorithms can reduce the computational load of finding the best split point, the dataset still needs to be traversed during node splitting;

2. The space complexity of the pre-sorting process is too high, as it requires storing feature values and the indices of the gradient statistics corresponding to the features, effectively consuming double the memory.

LightGBM

LightGBM, proposed by Microsoft, is mainly used to solve the problems encountered by GDBT in massive data, so it can be better and faster used in industrial practice.From the name LightGBM, we can see that it is a lightweight (Light) gradient boosting machine (GBM), which has the characteristics of faster training speed and lower memory usage compared to XGBoost.The following figure compares the memory and training time of XGBoost, XGBoost_hist (XGBoost using gradient histogram), and LightGBM under different datasets:

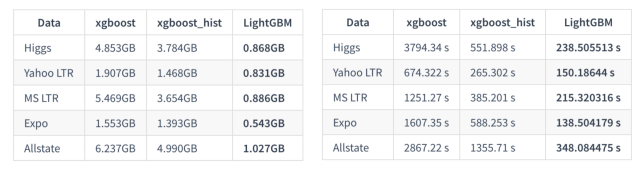
So how does LightGBM achieve faster training speed and lower memory usage?We have just analyzed the disadvantages of XGBoost, and LightGBM has proposed the following solutions to address these issues:

1. Single-side gradient sampling algorithm;
2. Histogram algorithm;
3. Exclusive feature bundling algorithm;
4. Leaf-wise vertical growth algorithm based on maximum depth;
5. Optimal splitting of categorical features;
6. Feature parallelism and data parallelism;
7. Cache optimization.

This section will continue to introduce LightGBM from the perspectives of mathematical principles and engineering implementation.2.1 Mathematical Principles2.1.1 Single-Side Gradient Sampling AlgorithmThe gradient size of the GBDT algorithm can reflect the weight of the samples; the smaller the gradient, the better the model fits. The single-side gradient sampling algorithm (Gradient-based One-Side Sampling, GOSS) utilizes this information to sample the samples, reducing a large number of samples with small gradients, focusing only on samples with high gradients in the subsequent calculations, significantly reducing the computational load.The GOSS algorithm retains samples with large gradients and performs random sampling on samples with small gradients. To avoid changing the data distribution of the samples, a constant is introduced for the small gradient samples during the gain calculation to balance.The specific algorithm is as follows:

We can see that GOSS sorts the samples based on the absolute value of the gradient in advance (without saving the sorted results), then takes the top a% of samples with large gradients and the remaining b%, and during the gain calculation, the weights of the small gradient samples are amplified by multiplying by rac{1-a}{b}.On one hand, the algorithm focuses more on under-trained samples, and on the other hand, it prevents sampling from significantly affecting the original data distribution by introducing weights.2.1.2 Histogram Algorithm

1. Histogram Algorithm

The basic idea of the histogram algorithm is to discretize continuous features into k discrete features while constructing a histogram with a width of k for statistical information (containing k bins).Using the histogram algorithm, we do not need to traverse the data; we only need to traverse k bins to find the best split point.We know that feature discretization has many advantages, such as easy storage, faster computation, strong robustness, and more stable models.For the histogram algorithm, the most direct advantages are as follows (taking k=256 as an example):

• Smaller memory usage:XGBoost requires 32-bit floating-point numbers to store feature values and 32-bit integers to store indices, while LightGBM only needs 8 bits to store histograms, reducing memory usage by 1/8;
• Lower computational cost:When calculating feature split gains, XGBoost needs to traverse the data once to find the best split point, while LightGBM only needs to traverse k times, directly reducing the time complexity from O(#data * #feature) to O(k * #feature), and we know that #data >> k.

Although discretizing features may not find the exact split points, it may have a certain impact on model accuracy, but the coarser splits also serve as a form of regularization, reducing model variance to some extent.

1. Histogram Acceleration

When constructing the histogram of leaf nodes, we can also reduce half of the computational load by constructing it through the difference between the histogram of the parent node and that of adjacent leaf nodes.In practical operation, we can first calculate the histogram of smaller leaf nodes and then use the histogram difference to obtain the larger leaf node’s histogram.

1. Sparse Feature Optimization

XGBoost considers only non-zero values during pre-sorting for acceleration, while LightGBM adopts a similar strategy:It only uses non-zero features to construct the histogram.2.1.3 Exclusive Feature Bundling AlgorithmHigh-dimensional features are often sparse, and features may be mutually exclusive (e.g., two features cannot be non-zero simultaneously). If two features are not completely exclusive (e.g., only a part of them cannot be non-zero simultaneously), the exclusivity can be represented by the mutual exclusion rate.The Exclusive Feature Bundling (EFB) algorithm indicates that if some features are merged, the number of features can be reduced.Regarding this idea, we will encounter two problems:

1. Which features can be bound together?
2. After feature binding, how to determine the feature values?

For the first problem:The EFB algorithm constructs a weighted undirected graph using the features and their relationships and converts it into a graph coloring algorithm.We know that graph coloring is an NP-Hard problem, so a greedy algorithm is used to obtain an approximate solution; the specific steps are as follows:

1. Construct a weighted undirected graph, where vertices are features and edges represent the degree of mutual exclusivity between two features;
2. Sort nodes in descending order based on their degree; the higher the degree, the greater the conflict with other features;
3. Traverse each feature, assigning it to an existing feature bundle or creating a new feature bundle, minimizing overall conflict.

The algorithm allows for features that are not completely exclusive to increase the number of feature bundles by setting a maximum mutual exclusion rate to balance the algorithm’s accuracy and efficiency. The pseudo-code of the EFB algorithm is as follows:

We see that the time complexity is O(#feature^2), which can handle a small number of features, but if the feature dimension reaches millions, the computational load will be very large. To improve efficiency, we propose a faster solution:Change the strategy of sorting based on node degree in the EFB algorithm to sorting based on the number of non-zero values, as the more non-zero values, the greater the probability of mutual exclusivity.For the second problem:The paper provides a feature merging algorithm, which is key to ensuring that original features can be separated from merged features.Assuming there are two feature values in the Bundle, A takes values [0, 10] and B takes values [0, 20], to ensure the exclusivity of features A and B, we can add an offset to feature B to convert it to [10, 30]. Thus, the merged feature will take values [0, 30], achieving feature merging.The specific algorithm is as follows:

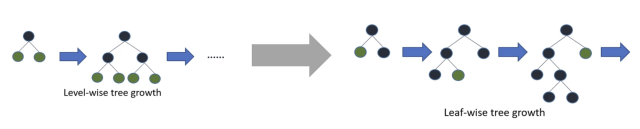
2.1.4 Leaf-wise Growth Algorithm with Depth LimitationIn the process of building trees, there are two strategies:

• Level-wise:Grow based on layers until stopping conditions are met;
• Leaf-wise:Split the leaf node with the highest gain each time until stopping conditions are met.

XGBoost adopts a Level-wise growth strategy, facilitating parallel computation of split nodes at each layer, which improves training speed but also increases unnecessary splits due to small node gains, thereby increasing computational load;LightGBM adopts a Leaf-wise growth strategy to reduce computational load, combined with maximum depth limitations to prevent overfitting. Since the maximum gain node needs to be calculated each time, parallel splitting cannot be achieved.

2.1.5 Optimal Splitting of Categorical FeaturesMost machine learning algorithms do not directly support categorical features; they generally encode categorical features before inputting them into the model.Common methods for handling categorical features include one-hot encoding, but we know that using one-hot encoding for decision trees is not recommended:

1. It can lead to imbalanced sample splits, resulting in very small split gains.For example, nationality splits can lead to features like whether it’s Chinese or American, and this series of features only has a few samples equal to 1, while most samples are 0.This kind of split gain is very small:The smaller split sample set accounts for too little of the total sample.No matter how large the gain is, after multiplying by that proportion, it can almost be ignored;The larger split sample set is almost the original sample set, yielding almost zero gain;
2. It affects decision tree learning:Decision trees rely on statistical information from the data, while one-hot encoding scatters the data into small, fragmented spaces.Statistical information in these small fragmented spaces is inaccurate, leading to poorer learning performance.Essentially, this is because the predictive capability of features after one-hot encoding is reduced, and the predictive ability of the feature is artificially divided into multiple parts, each competing with other features for optimal split points and ultimately failing; thus, the importance of that feature will be lower than its actual value.

LightGBM natively supports categorical features, using a many-vs-many splitting method to divide categorical features into two subsets, achieving optimal splitting of categorical features.Assuming a certain dimension feature has k categories, there are 2^{(k-1)} – 1 possibilities, with a time complexity of O(2^k). LightGBM implements O(klog_2k) time complexity based on Fisher’s paper “On Grouping For Maximum Homogeneity”.

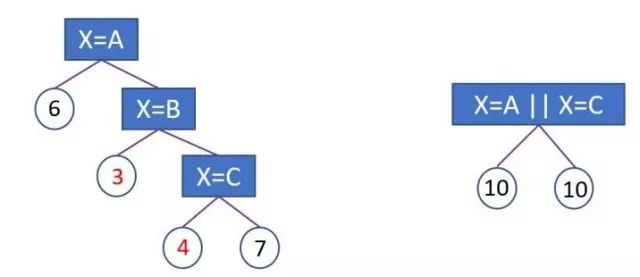
The left side of the image shows the split based on one-hot encoding, while the right side shows LightGBM’s many-vs-many splitting. Under the same depth, the latter can learn a better model.The basic idea is that each time grouping, the categorical features are classified according to the training objectives, sorting based on their cumulative values rac{ ext{sum gradient}}{ ext{sum hessian}} on the histogram, and then finding the best split on the sorted histogram.Additionally, LightGBM adds regularization constraints to prevent overfitting.

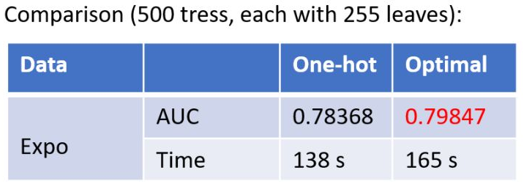
We can see that this method of handling categorical features improved the AUC by 1.5 points, with only a 20% increase in time.2.2 Engineering Implementation2.2.1 Feature ParallelismTraditional feature parallel algorithms involve vertically partitioning the data, then using different machines to find the optimal split points for different features, integrating the best split points through communication, and informing other machines of the split results.Traditional feature parallel methods have a significant drawback:They require informing each machine of the final split results, adding extra complexity (as data is vertically partitioned, each machine contains different data, and the splitting results need to be communicated).LightGBM does not perform vertical data partitioning; each machine has the complete training set data, and after obtaining the optimal split scheme, the split can be executed locally, reducing unnecessary communication.2.2.2 Data ParallelismTraditional data parallel strategies mainly involve horizontally partitioning the data, then building local histograms and integrating them into a global histogram, finally finding the best split point in the global histogram.This method has a significant disadvantage:The communication overhead is too high.If using point-to-point communication, the communication overhead for one machine is approximately O(#machine * #feature *#bin);If using integrated communication, the communication overhead is O(2 * #feature *#bin);LightGBM adopts a scatter-reduce approach to distribute the task of integrating histograms across different machines, thereby reducing communication costs, and further reducing communication between different machines through histogram differences.2.2.3 Voting ParallelismIn cases where the data volume is particularly large and features are also numerous, voting parallelism can be employed.Voting parallelism mainly optimizes the bottleneck of communication costs during data merging in data parallelism by merging only a portion of the histogram of features through voting to reduce communication volume.The general steps are two:

1. Identify the Top K features locally and filter out features that may be optimal split points based on voting;
2. During merging, only merge the features selected by each machine.

2.2.4 Cache OptimizationAs mentioned earlier, XGBoost’s pre-sorted features access sample gradient statistics through indices, and the non-contiguous nature of index access can lead to cache misses, affecting performance.While XGBoost proposed a cache access optimization algorithm to address this issue, the histogram algorithm used by LightGBM is inherently cache-friendly:

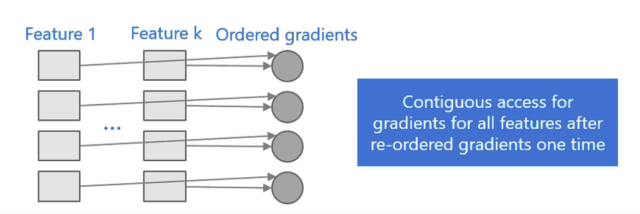
1. First, all features use the same method to obtain gradients (unlike different features obtaining gradients through different indices), allowing for continuous access to sorted gradients, greatly improving cache hits;
2. Additionally, because it does not need to store indices from features to samples, it reduces storage consumption and avoids cache miss issues.

2.3 Comparison with XGBoostThis section mainly summarizes the advantages of LightGBM compared to XGBoost, introducing them from the aspects of memory and speed.2.3.1 Smaller Memory Footprint

1. XGBoost requires pre-sorting, storing both feature values and the indices of their corresponding sample statistics, while LightGBM uses the histogram algorithm to convert feature values into bin values, eliminating the need for indices from features to samples, reducing space complexity from O(2*#data) to O(#bin), significantly decreasing memory consumption;
2. LightGBM uses the histogram algorithm to convert storage from feature values to bin values, further lowering memory consumption;
3. LightGBM employs the exclusive feature bundling algorithm during training to reduce the number of features, thus lowering memory consumption.

2.3.2 Faster Speed

1. LightGBM adopts the histogram algorithm to change the traversal of samples to traversing histograms, greatly reducing time complexity;
2. LightGBM uses the single-side gradient algorithm to filter out samples with small gradients, reducing a significant amount of computation;
3. LightGBM employs a leaf-wise growth strategy to construct trees, reducing unnecessary computational loads;
4. LightGBM utilizes optimized feature parallelism and data parallelism methods to accelerate computation, and can also use voting parallelism strategies when the data volume is very large;
5. LightGBM also optimizes cache, increasing cache hit rates.

References

1. XGBoost: A Scalable Tree Boosting System
2. Chen Tianqi’s paper presentation PPT
3. What are the differences between GBDT and XGBOOST in machine learning algorithms? – wepon’s answer – Zhihu
4. LightGBM: A Highly Efficient Gradient Boosting Decision Tree
5. LightGBM documentation
6. Paper reading – Principles of LightGBM
7. Machine learning algorithms of LightGBM
8. Should one-hot encoding be used for decision trees in sklearn? – Ke Guolin’s answer – Zhihu
9. How to master LightGBM
10. A Communication-Efficient Parallel Algorithm for Decision Tree.