Understanding Transformer Positional Encoding

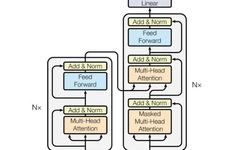
Possibly the most frequently seen image in the NLP field

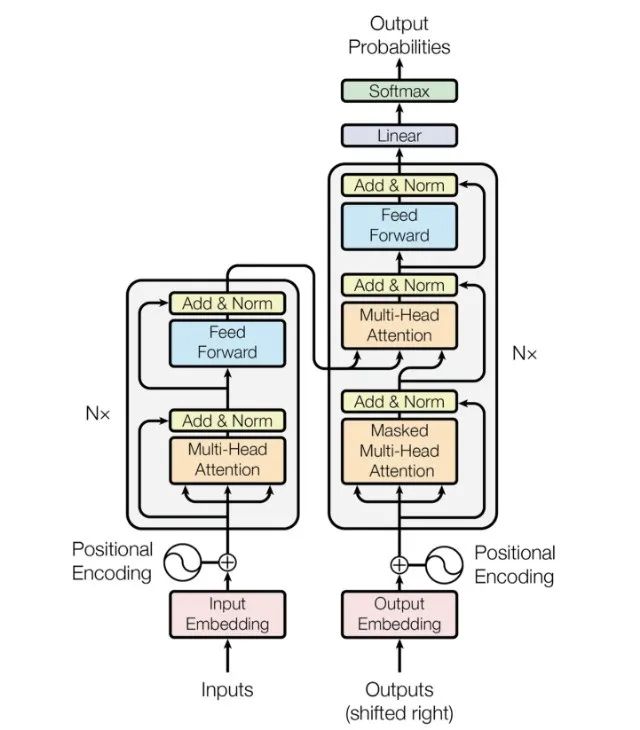
In the Transformer structure, the left side is called the encoder, and the right side is the decoder. Do not underestimate these two components; the left encoder eventually evolved into the renowned Bert, while the right decoder recently transformed into the well-known GPT model. From this description, we can see how significant the Transformer model is for the NLP field, and its influence is expanding into other domains.

So the question arises,what exactly does the Transformer do?

Answer: The key breakthrough of the Transformer is Self-attention, which allows NLP models to input data in parallel like CV models.

In the field of Natural Language Processing (NLP), the model’s input is a sequence of text.

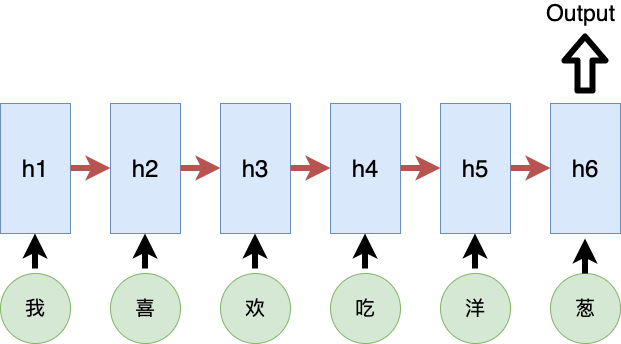
In previous models, each sequence in NLP was input into the model token by token. For example, for the sentence “I like to eat onions”, the input sequence would be “I”, “like”, “to”, “eat”, “onion”, one character at a time.

This input method introduces a problem. If a model only consumes one character at a time, it can only learn the information of the two adjacent characters and cannot grasp the meaning of the entire sentence. To solve this issue, the Transformer model employs Self-attention. The input method for Self-attention is as follows:

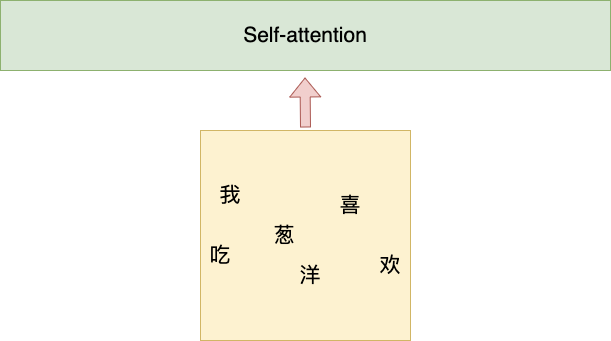
We can see that Self-attention allows all characters to be treated as input simultaneously. However, the input in NLP has specific characteristics; the text must be input in a certain order because the sequence carries semantic relationships. For example, the following two sentences have different meanings due to their word order.

Sentence 1: I like to eat onions

Sentence 2: Onions like to eat me

Therefore, for the Transformer structure, to better utilize the parallel input feature, the first problem to solve is to ensure that the input content possesses positional information. In the original paper, to introduce positional information, a Position mechanism was added.

For the Transformer, the Position mechanism appears simple but is actually not easy to understand. This article will clarify how positional information is introduced and then explain in detail how it is implemented in the Transformer. Finally, we will mathematically prove why this encoding method can introduce relative positional information.

Types of Positional Encoding

In general, positional encoding can be divided into two types: functional and tabular.

Functional: Positional encoding is obtained by inputting token positional information.

Tabular: A vocabulary of length L is established, assigning position IDs according to the vocabulary length.

Previous Methods – Tabular

Method 1: Allocation in the Range [0,1]

This method allocates values in the range of 0 to 1, assigning 0 to the first token and 1 to the last token, with the remaining tokens allocated evenly based on the length of the text. The specific form is as follows:

I like to eat onions 【0 0.16 0.32…..1】

I really don’t like to eat onions【0 0.125 0.25…..1】

Issue: We can see that if the sentence lengths differ, the positional encodings will be different, so they cannot represent similarities between sentences.

Method 2: Allocation in the Range of Positive Integers 1-n

This method is more intuitive, allocating values based on the order of input tokens corresponding to their index positions. The specific form is as follows:

I like to eat onions 【1, 2, 3, 4, 5, 6】

I really don’t like to eat onions【1, 2, 3, 4, 5, 6, 7】

Issue: Typically, as sentences grow longer, the later values increase, indicating that the weight of that position is greater, which fails to highlight the true weight of each position.

Summary

Previous methods have their shortcomings, prompting the Transformer to improve the encoding of positional information.

Relative Position Relationships – Functional

The characteristic of relative position encoding focuses on the relative position (distance of several tokens) between one token and another. The distance between position 1 and position 2 is closer than that between position 3 and position 10; the distance between position 1 and position 2, and between position 3 and position 4, is only 1.

Using the example of “I like to eat onions”, let’s see what the relative position relationship looks like:

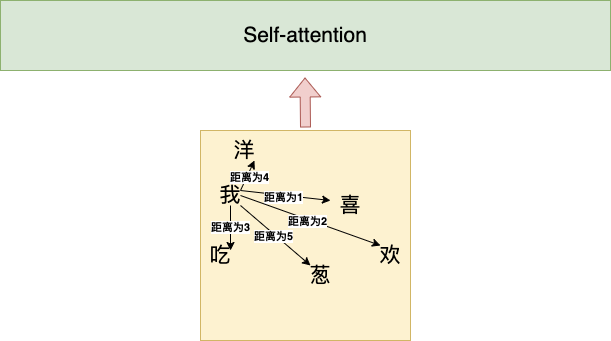
We can see that using the relative position method, we can clearly understand the distance relationships between words.

Transformer’s Position

Type

First, let’s define: The positional information in the Transformer is functional. The formula provided in the GPT-3 paper is as follows:

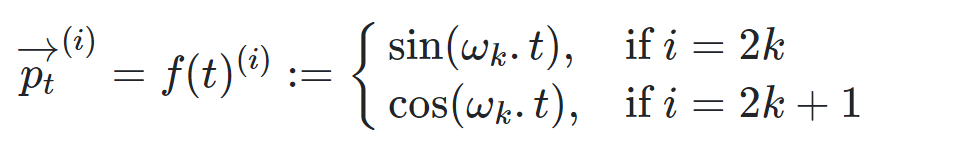
Details:

First, note that the positional information encoding for each token given in the previous formula is not a number, but a vector segmented by different frequencies, with the same dimension as the text. The vector is shown as:

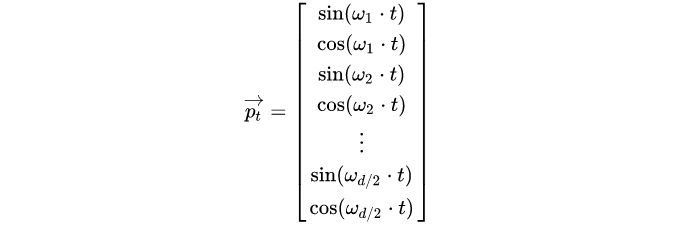
Different frequencies are represented by .

After obtaining the position vector P, it is added to the model’s embedding vector to obtain the final representation that enters the Transformer model.

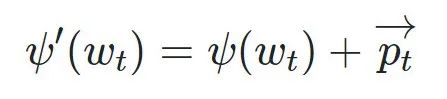
Explanation of Each Element:

① About :

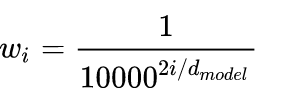
is the frequency

② About

Here, represents the position of each token, such as position 1, position 2, and position n.

Why Can It Represent Relative Distances?

As mentioned earlier, this method of representing positional information can indicate the relative relationship between tokens at different distances. Here, we will prove this mathematically.

Simple Review

Let’s review the trigonometric sine and cosine formulas from middle school:

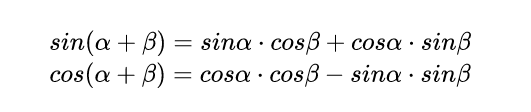
Start Proof

We know that the position of a certain token is , if a certain token is represented as , that indicates this position is at a distance of from the previous token.

If we need to examine the relationship between positions and , we can calculate the positional encoding according to the positional encoding formula, resulting in:

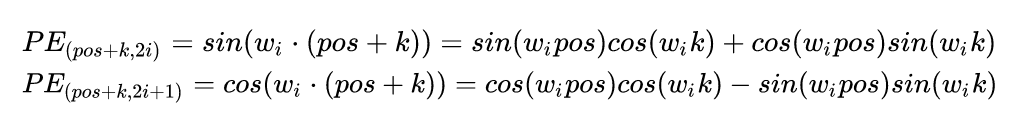
We can observe that there is a familiar part in the above formula:

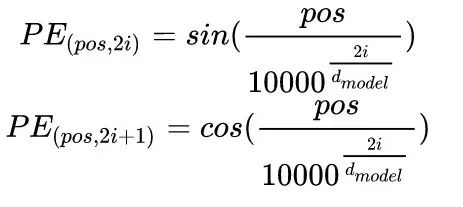
According to the above formula, we can see that the familiar part is brought into the formula for , and the result after substitution is as follows:

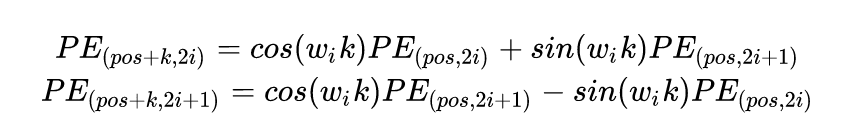
We can see that the distance K is a constant, and all the computed values in the above formula are also constants, which can be expressed as:

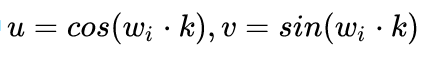
This can be expressed as a matrix multiplication.

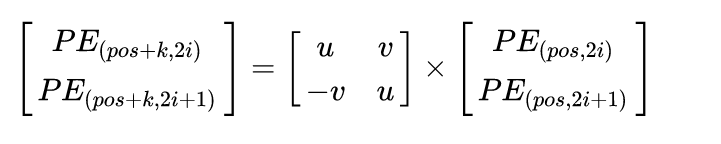
From the perspective of the above matrix multiplication, we can see that the positional encoding and positional encoding are linearly related.

So the question arises, the above operations only reveal a linear relationship; how can we more explicitly know the distance relationship of each token?

To answer the above question, we will multiply the vectors (the product of two vectors) to obtain the following result:

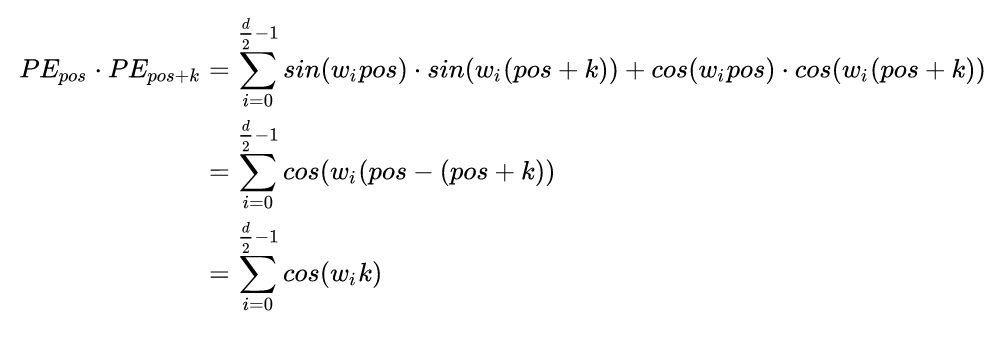
We find that the result after multiplication is a sum of cosine values. The influencing factor is . If the distance between two tokens is greater, meaning K is larger, according to the properties of the cosine function, the product result of the two positions will be smaller. Thus, we can conclude that if two tokens are farther apart, the product result will be smaller.

Others

Although this method can represent relative distance relationships, it also has limitations. One significant issue is that it can only obtain relative relationships and cannot determine directional relationships. The so-called directional relationship refers to whether one token is in front of or behind another, which cannot be judged. The mathematical representation is as follows:

Reference

1.https://kazemnejad.com/blog/transformer_architecture_positional_encoding/

2.https://zhuanlan.zhihu.com/p/121126531

3.https://timodenk.com/blog/linear-relationships-in-the-transformers-positional-encoding/