Originally from AI有道
Seven years ago, the paper “Attention is All You Need” introduced the transformer architecture, revolutionizing the entire field of deep learning.
Today, all major models are based on the transformer architecture, yet the internal workings of the transformer remain a mystery.
Last year, one of the authors of the transformer paper, Llion Jones, announced the establishment of an artificial intelligence company called Sakana AI. Recently, Sakana AI published a paper titled “Transformer Layers as Painters,” exploring the flow of information in pretrained transformers and conducting a series of experiments on frozen transformer models with only decoders and only encoders. Note that this research did not involve any type of fine-tuning of the pretrained models.

Paper link: https://arxiv.org/pdf/2407.09298v1
The study suggests that the internal mechanisms of transformers (especially the intermediate layers) can be understood as analogous to a painter’s workflow.
The painting workflow typically involves passing a canvas (input) to a series of painters. Some painters excel at painting birds, while others are skilled at painting wheels. Each painter receives the canvas from their lower-level painter and then decides whether to add some strokes to the painting or simply pass it on to their upper-level painter (using residual connections).
This analogy is not a strict theory but a tool for thinking about transformer layers. Inspired by this analogy, the study tested several hypotheses:
-
Do all layers use the same representation space?
-
Are all layers necessary?
-
Do intermediate layers perform the same function?
-
Is the order of the layers important?
-
Can these layers run in parallel?
-
Is the order more important for certain tasks than other factors?
-
Does looping help with layer parallelism?
-
Which variants have the least impact on model performance?
The study conducted a series of experiments on pretrained LLMs, including testing variations in standard transformer execution strategies and measuring the impact of these changes on model performance across various benchmarks for only decoder (Llama) and only encoder (BERT) models.
Do all layers use the same representation space?
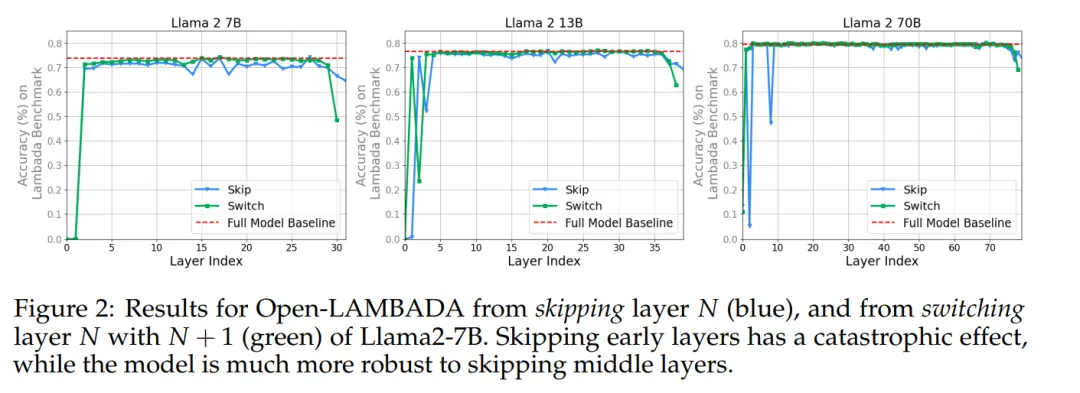
To determine whether different layers use the same representation space, the authors tested whether the transformer is robust when skipping specific layers or switching the order of adjacent layers. For instance, in Llama2-7B, the 6th layer typically expects to receive output from the 5th layer. If the 6th layer is given output from the 4th layer, will it exhibit “catastrophic” behavior?
In Figure 2, we can see that, except for the first layer and the last few layers, the layers of Llama2-7B are quite robust to skipping layers or switching layers.
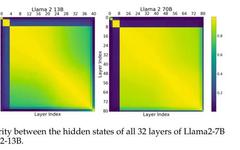
This experiment indicates that the intermediate layers share a representation space, while having a different representation space from the “outer layers” (the first and last layers). To further validate this hypothesis, the authors followed previous research and measured the average cosine similarity of hidden state activations between different layers of the models (Llama2-7B, Llama2-13B, and BERT-Large) in the benchmarks. Figure 3 shows the consistency among all intermediate layers.
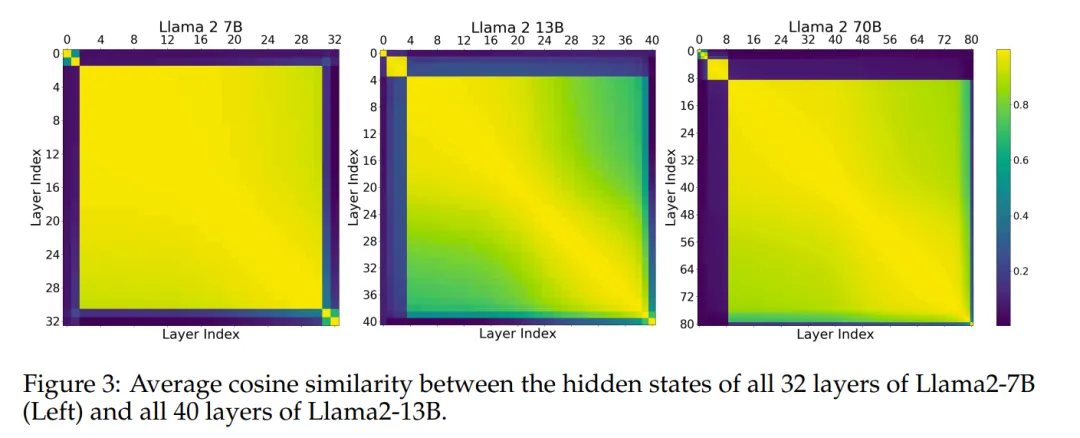
This suggests that the model may have three different representation spaces for the “start,” “middle,” and “end” layers. Answering question 1: Yes, the intermediate layers seem to share a common representation space.
Are all layers necessary?
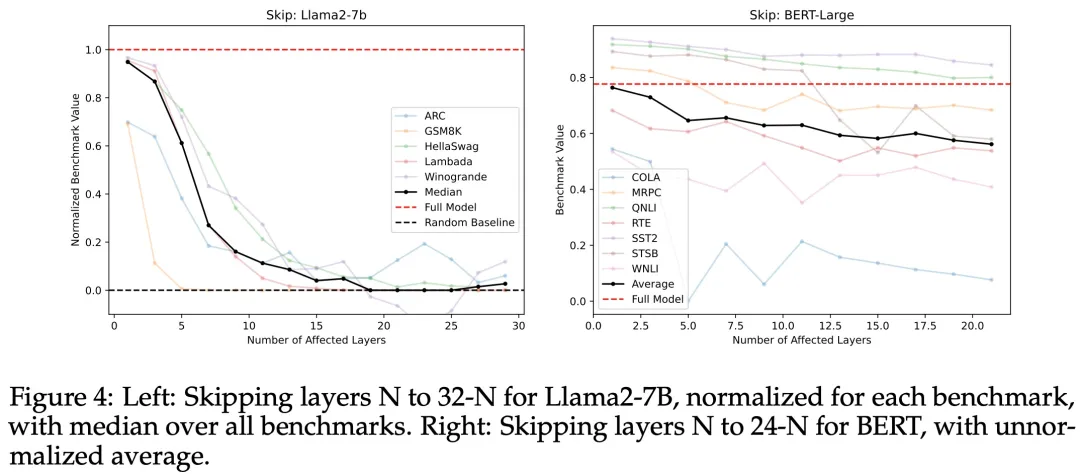
To further test whether the intermediate layers share a redirection space (in addition to having similar cosine similarity), the study attempted “skipping layers,” which involves sending the output of the Nth layer directly to the input of the N + M layer (where M > 1), effectively “skipping” M – 1 layers, as shown in Figure 1a. This experiment aimed to see if the N + M layer could understand the activations of the N layer, even though it was trained only based on inputs from the N + M – 1 layer. Figure 4 shows that Llama2-7B and BERT-Large experienced moderate performance drops on many benchmarks. Answering question 2: Are all layers necessary?
No, at least some intermediate layers can be removed without catastrophic failure.
Do intermediate layers perform the same function?
If intermediate layers share a common representation space, does this mean that the other intermediate layers are redundant? To test this, the researchers reran the “skipping” experiment from the previous subsection, replacing the weights of the intermediate layers with the weights of the central layer, effectively cycling T – 2N + 1 times on each replaced layer, where T is the total number of layers (Llama2-7B has 32 layers, BERT-Large has 24 layers).
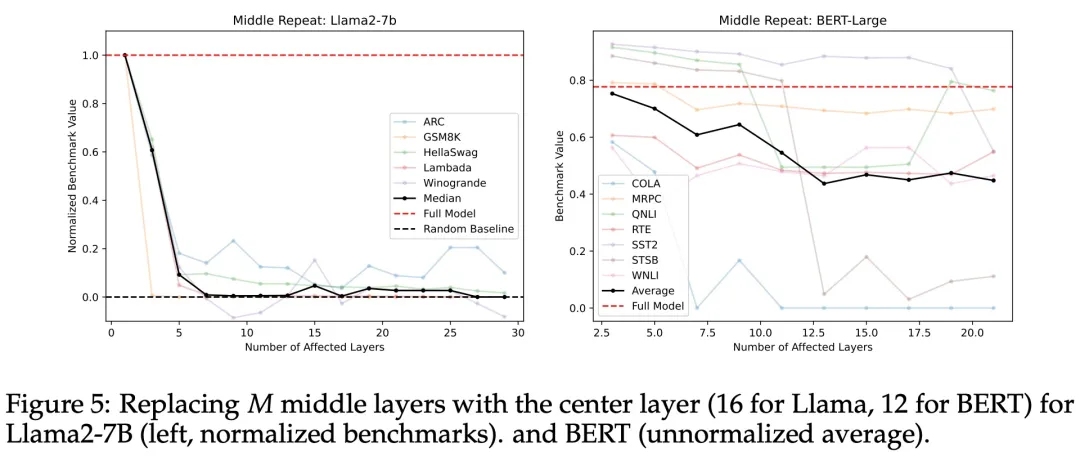
As shown in Figure 5, it can be observed that as the number of replaced layers increases, the model’s scores on the benchmarks drop rapidly. From Figure 11 later, it can be seen that this method of replacing layers performed worse than other methods attempted by the researchers. Therefore, the researchers concluded that intermediate layers perform different functions, and sharing weights among intermediate layers is not feasible.
Is the order of the layers important?
Previous experiments indicated that intermediate layers share a representation space but are responsible for different functions. The next question to address is what significance the order of these functions holds. To tackle this, the researchers designed two sets of experiments. First, they ran the intermediate layers in the reverse order of training. Specifically, they took the output of the T – N layer, input it into the T – N – 1 layer, and then input that layer’s output into the T – N – 2 layer, and so on, until the N layer, then sent that layer’s output to the subsequent T – N layers. In the second set of experiments, the researchers ran the intermediate layers in random order and averaged over 10 seed values.
Figures 6 and 7 show the results of running intermediate layers in reverse and random order, respectively, with the model showing a gradual decline across all benchmark test sets. This also indicates that while the order of layers is somewhat important for the model, even when the order is changed, these layers can still function.
Interestingly, randomizing the order of the layers performed better than completely reversing them. This may be because the randomized order retains some of the original relationships between the layers (i.e., layer i comes after layer j, where i > j), while completely reversing them breaks these relationships entirely.
Can these layers run in parallel?
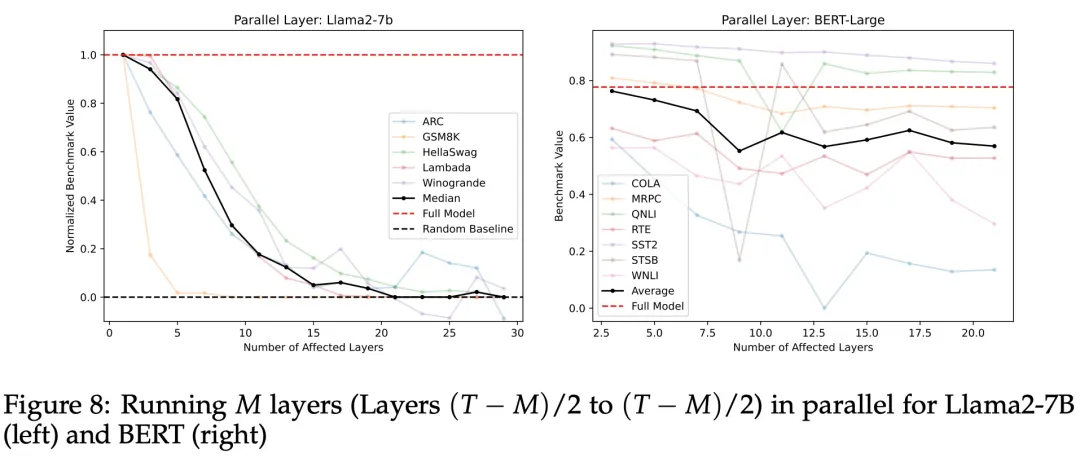
To verify that the layers themselves have more importance than the order of execution, the researchers designed an experiment to run the intermediate layers in parallel and send their average results to the final N layers.
As shown in Figure 8, the model exhibited a gradual downward trend in performance across all benchmark tests; however, this trend did not apply to mathematical applications in GSM8K.
The experimental results indicate that this method is generally effective in most cases, but it does not perform well on some complex mathematical problems. This parallel processing method is better than simply skipping some layers, but not as effective as running the layers in reverse order. Based on this, the researchers concluded that running layers in parallel is feasible in general, but may not be suitable for mathematical problems that require sequential logical understanding.
Is the order more important for certain tasks than other factors?
For most modified models facing abstract reasoning (ARC) or mathematical reasoning (GSM8K) benchmark tests, they often show the steepest decline in performance. This phenomenon may stem from the sensitivity of step-by-step reasoning tasks to the order of model layers, which is far higher than that of tasks primarily relying on semantic understanding. Unlike tasks that can be accomplished merely through understanding semantics, reasoning tasks require models to grasp both structure and meaning. This observation aligns with the assumption that models may engage in some degree of sequential dependency reasoning during single processing.
The researchers used a metaphor to illustrate: if creating a collage composed of many different elements, the order of painting may not be so important; but if one is to paint a precise architectural scene, the order of each stroke becomes very important. Accordingly, the researchers concluded that mathematical and reasoning tasks have a higher dependency on the order of model layers, while the impact of order is relatively smaller for tasks primarily relying on semantic understanding.
Does looping help with layer parallelism?
Continuing with the painting metaphor from the previous section, when a painter works on a painting, they do not start by painting everything at once; instead, they first paint a part, like the body of a car, and then based on that part, they add other elements, such as the wheels. In AI models, the layers are the so-called painters, and processing information is akin to painting. If the correct information is obtained first, that is, the body of the car is painted first, then they can better complete their work by adding the wheels.
For transformers, when given appropriate input, layers may contribute only during forward propagation and not through residual connections “passing” inputs. If this is the case, then iterating on parallel layers from the previous experiment should improve model performance more than executing parallel layers once. Based on this, the researchers tested this by feeding the average output of the parallel layers back into the same layer for a fixed number of iterations.
Figure 9 shows the results of looping the parallel layers three times. The results of looping in parallel three times significantly outperformed a single iteration (parallel layers). When the starting layer N is set to 15 (for the Llama2-7B model) or 11 (for the BERT model), it is at the extreme left endpoint of each case, affecting only a single layer. In this specific case, the effect of three iterations in parallel is equivalent to simply repeating the intermediate layers three times. Meanwhile, for the parallel layers in this regard, their performance is indistinguishable from that of the full model.
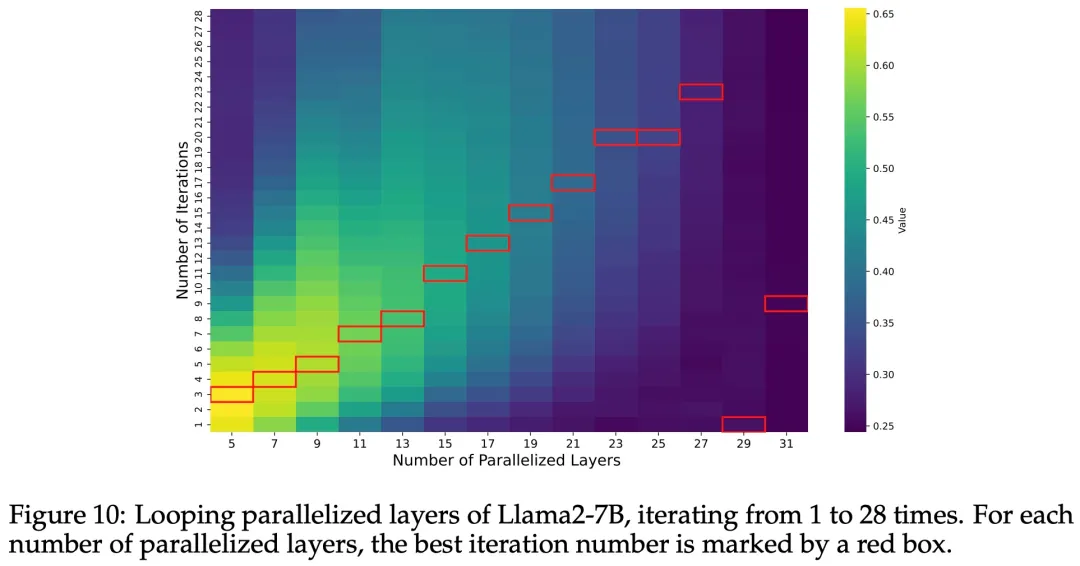
The researchers also repeated the same experiment for different numbers of iterations. Figure 10 shows the performance of Llama2-7B as the number of parallel layers M and the number of iterations changes. The highest performance iteration for each M is marked in red. Except for M=29 and M=31 (almost all layers parallelized), the optimal number of iterations is roughly linearly proportional to the number of parallelized layers. Therefore, the researchers concluded that the optimal number of iterations is proportional to the number of parallelized layers.
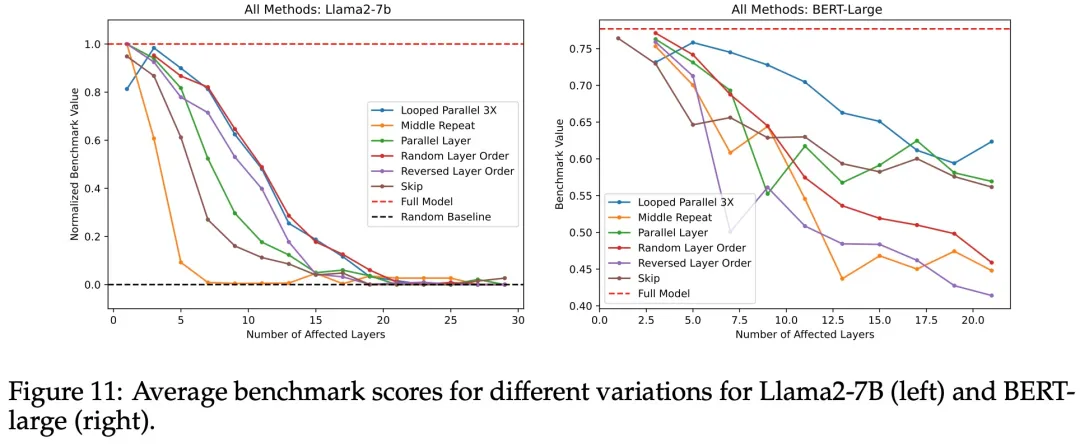
How to adjust layers to minimize the impact on model performance?
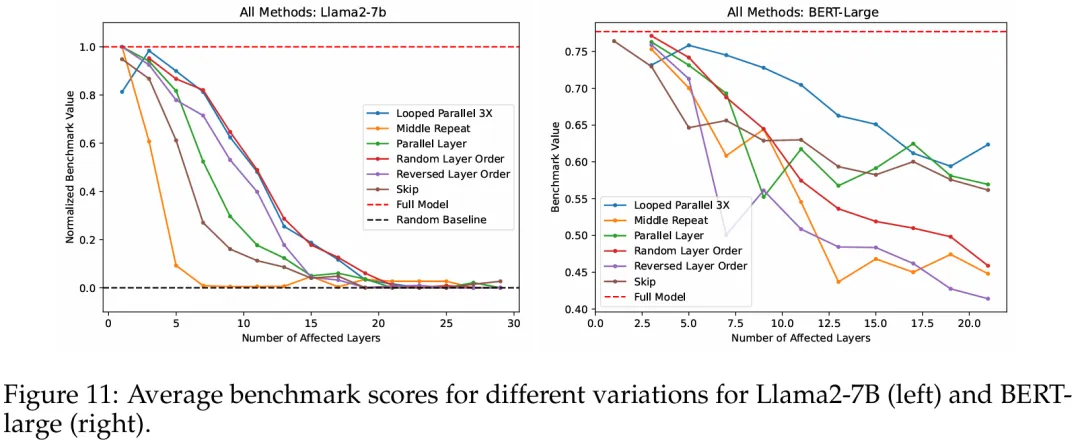
Finally, in Figure 11, the researchers compared all the “modifications” made to the transformer in all experiments, displaying the median or average across all benchmarks in a single chart.
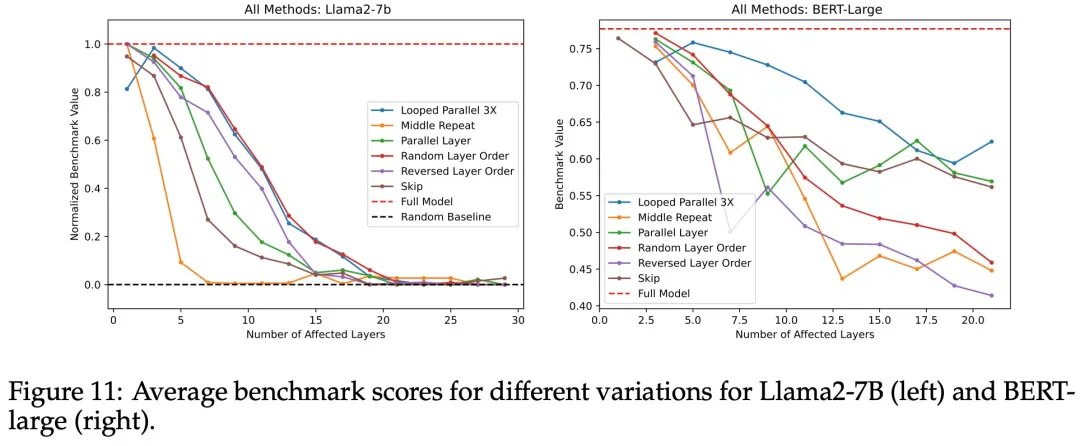
Intermediate repetition — replacing intermediate layers with the same number of intermediate layer copies — performed the worst, quickly dropping to the performance of the random baseline. In contrast, the impacts of looping in parallel and random layer order were minimal. Thus, the researchers concluded that the impact of repeating a single layer is the most severe. The impacts of randomizing layer order and looping in parallel are the least.
These experiments overall show a gradual decline in performance, but the researchers remain unclear why these layers maintain a certain robustness under most perturbations, a question that requires further exploration in future research.
For more details, please refer to the original paper.
Reference link: https://arxiv.org/pdf/2407.09298v1
Disclaimer: The content published by this public account is for learning and communication purposes only, and the copyright belongs to the original author. If your rights are infringed, please contact us in a timely manner, and we will delete the content as soon as possible. The content reflects the author’s personal views and does not represent the position of this public account or its authenticity.