Source: Python Data Science
This article is about 7200 words, recommended reading time 14 minutes.
In this article, we will explore the Transformer model and understand how it works.
1. Introduction
The BERT model launched by Google achieved state-of-the-art results in 11 NLP tasks, triggering a revolution in the NLP field. One key factor for BERT’s success is the powerful role of the Transformer. The Google Transformer model was initially used for machine translation tasks and achieved state-of-the-art performance at that time. The Transformer improved the slow training issue of RNNs by utilizing the self-attention mechanism for fast parallel processing. Additionally, the Transformer can be scaled to very deep levels, fully exploiting the characteristics of DNN models to enhance model accuracy. In this article, we will study the Transformer model and understand how it works.
2. Main Content Begins
The Transformer was proposed in the paper “Attention Is All You Need” and is now the recommended reference model for Google Cloud TPU. The TensorFlow code related to the paper can be obtained from GitHub as part of the Tensor2Tensor package. Harvard’s NLP team has also implemented a PyTorch version and annotated the paper.
In this article, we will attempt to simplify the model a bit and introduce the core concepts one by one, hoping to make it easy for the general reader to understand.
Attention Is All You Need:
https://arxiv.org/abs/1706.03762
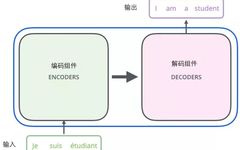
From a macro perspective, first, we can view this model as a black box operation. In machine translation, it means inputting one language and outputting another language.
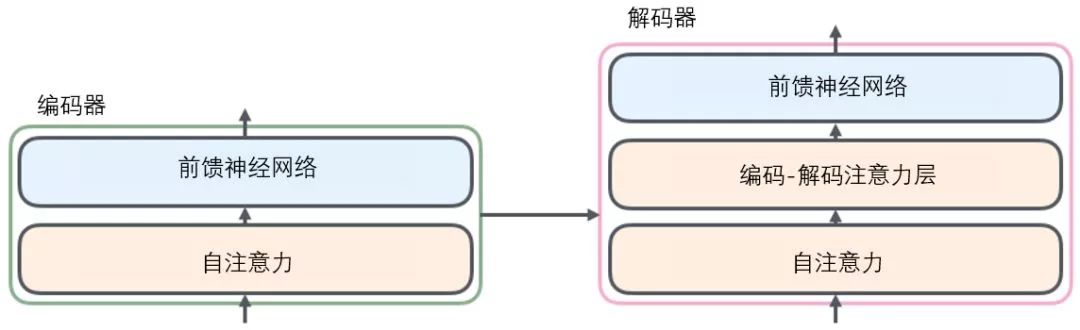
By unpacking this black box, we can see that it consists of an encoder component, a decoder component, and the connections between them.
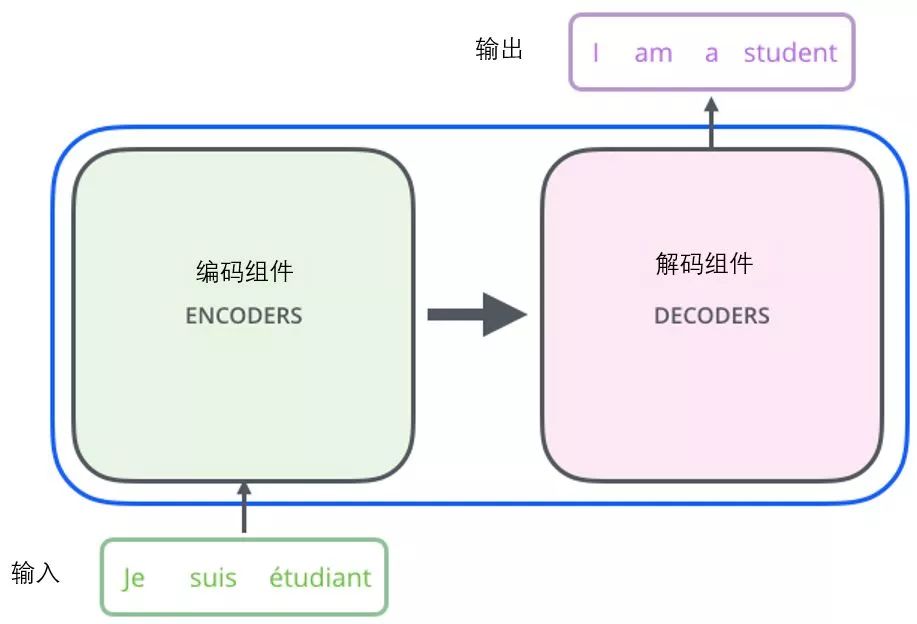
The encoder component is made up of a stack of encoders (the paper stacks 6 encoders together – the number 6 is not magical, you can try other numbers). The decoder component also consists of the same number of decoders corresponding to the encoders.
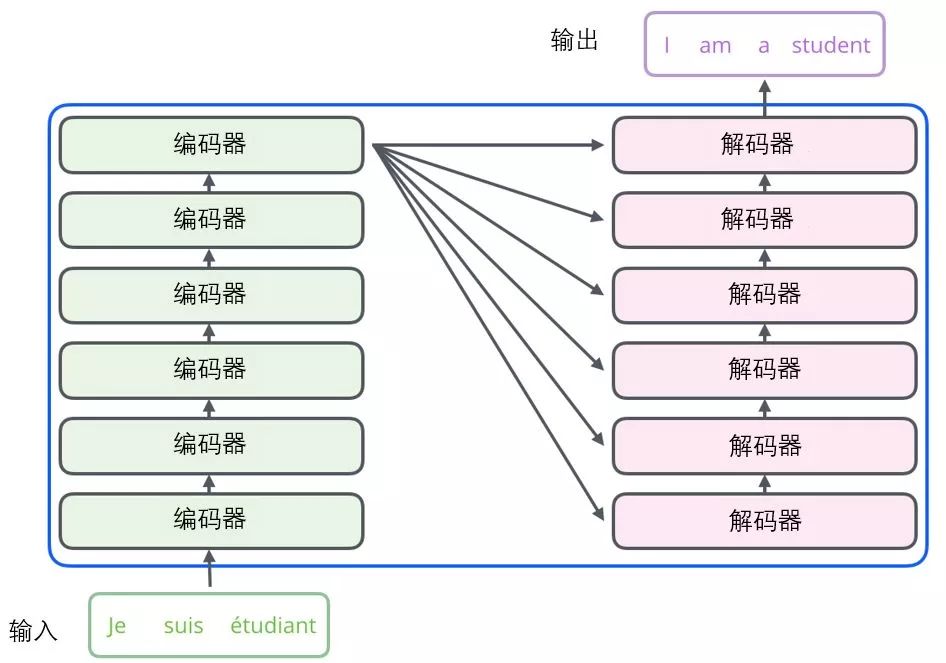
All encoders are structurally identical, but they do not share parameters. Each decoder can be decomposed into two sub-layers.
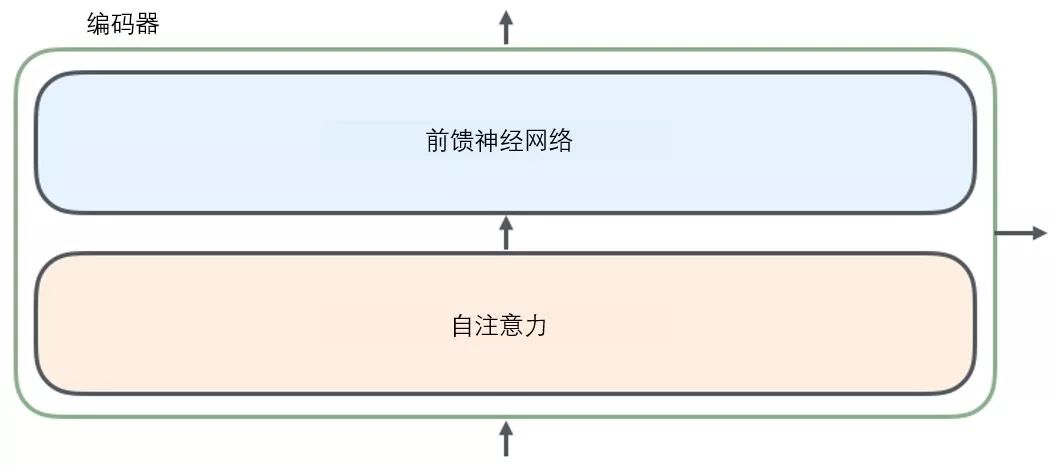
The sentences inputted into the encoder first pass through a self-attention layer, which helps the encoder pay attention to other words in the input sentence while encoding each word. We will explore self-attention in greater depth later in the article.
The output of the self-attention layer is passed to a feed-forward neural network. The feed-forward neural network corresponding to each word in each position is exactly the same (another interpretation is that it is a one-dimensional convolutional neural network with a window size of one word).
There is also a self-attention layer and a feed-forward layer in the decoder. In addition, there is an attention layer between these two layers to focus on relevant parts of the input sentence (similar to the attention mechanism of seq2seq models).
Introducing Tensors into the Picture
We have understood the main parts of the model, next, let’s take a look at how various vectors or tensors (note: the concept of tensors is a generalization of the concept of vectors, which can be simply understood that a vector is a first-order tensor, and a matrix is a second-order tensor) convert the input into output in different parts of the model.
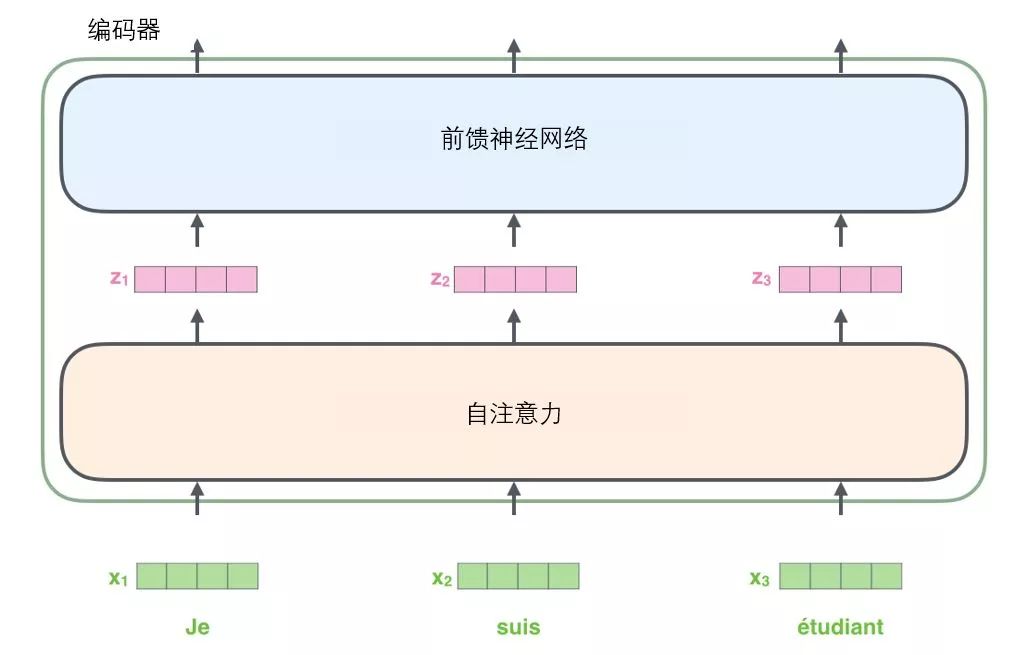
Like most NLP applications, we first convert each input word into a word vector through a word embedding algorithm.
Each word is embedded as a 512-dimensional vector, and we use these simple boxes to represent these vectors.
The word embedding process only occurs in the bottom layer of the encoder. All encoders share a common characteristic, that is, they receive a list of vectors, each vector in the list is of size 512 dimensions. In the bottom (initial) encoder, it is the word vector, but in other encoders, it is the output of the next layer encoder (which is also a list of vectors). The size of the vector list is a hyperparameter that we can set – generally, it is the length of the longest sentence in our training set.
After the input sequence is word embedded, each word will flow through two sub-layers in the encoder.
Next, let’s look at a core feature of the Transformer, where each word in the input sequence has its unique path flowing into the encoder. In the self-attention layer, there are dependencies between these paths. The feed-forward layer does not have these dependencies. Therefore, various paths can be executed in parallel during the feed-forward layer.
Then we will take a shorter sentence as an example to see what happens in each sub-layer of the encoder.
Now We Start “Encoding”
As mentioned above, an encoder receives a list of vectors as input, then passes the vectors in the list to the self-attention layer for processing, and then passes them to the feed-forward neural network layer, and the output result is passed to the next encoder.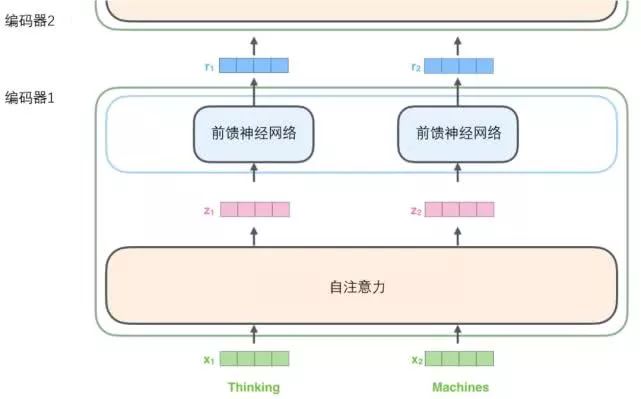
Each word in the input sequence undergoes a self-encoding process. Then, they each pass through the same feed-forward neural network – the same network for each vector, and each vector passes through it respectively.
Looking at the Self-Attention Mechanism from a Macro Perspective
Do not be confused by the term self-attention, as if everyone should be familiar with this concept. In fact, I also did not encounter this concept until I read the paper Attention Is All You Need. Let’s refine how it works.
For example, the following sentence is the input sentence we want to translate:
The animal didn’t cross the street because it was too tired
What does “it” refer to in this sentence? Does it refer to the street or the animal? This is a simple question for humans, but not for algorithms.
When the model processes the word “it”, the self-attention mechanism allows “it” to establish a connection with “animal”.
As the model processes each word in the input sequence, self-attention will pay attention to all words in the entire input sequence, helping the model better encode the current word.
If you are familiar with RNNs (Recurrent Neural Networks), recall how it maintains the hidden layer. RNNs combine the representations of all previously processed words/vectors with the current word/vector being processed. The self-attention mechanism incorporates the understanding of all relevant words into the word we are processing.
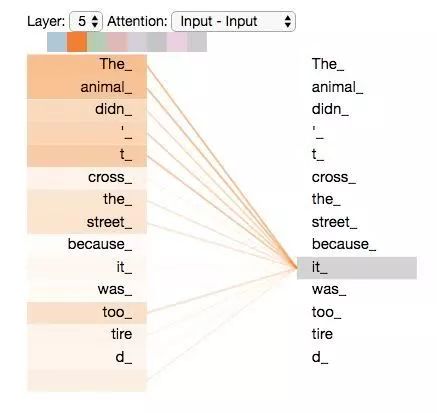When we are encoding the word “it” in encoder #5 (the top encoder in the stack), the attention mechanism will focus on “The Animal”, incorporating part of its representation into the encoding of “it”.
Please be sure to check the Tensor2Tensor notebook, where you can download a Transformer model and verify it interactively.
Looking at the Self-Attention Mechanism from a Micro Perspective
First, let’s understand how to calculate self-attention using vectors, and then see how it is implemented using matrices.
The first step in calculating self-attention is to generate three vectors from each input vector (the word vector for each word) of the encoder. That is, for each word, we create a query vector, a key vector, and a value vector. These three vectors are created by multiplying the word embeddings with three weight matrices.
It can be observed that these new vectors have lower dimensions than the word embedding vectors. Their dimension is 64, while the dimensions of the word embedding and input/output vectors of the encoder are 512. However, it is not strictly required for the dimensions to be smaller; this is just an architectural choice that keeps most of the calculations of multi-headed attention unchanged.
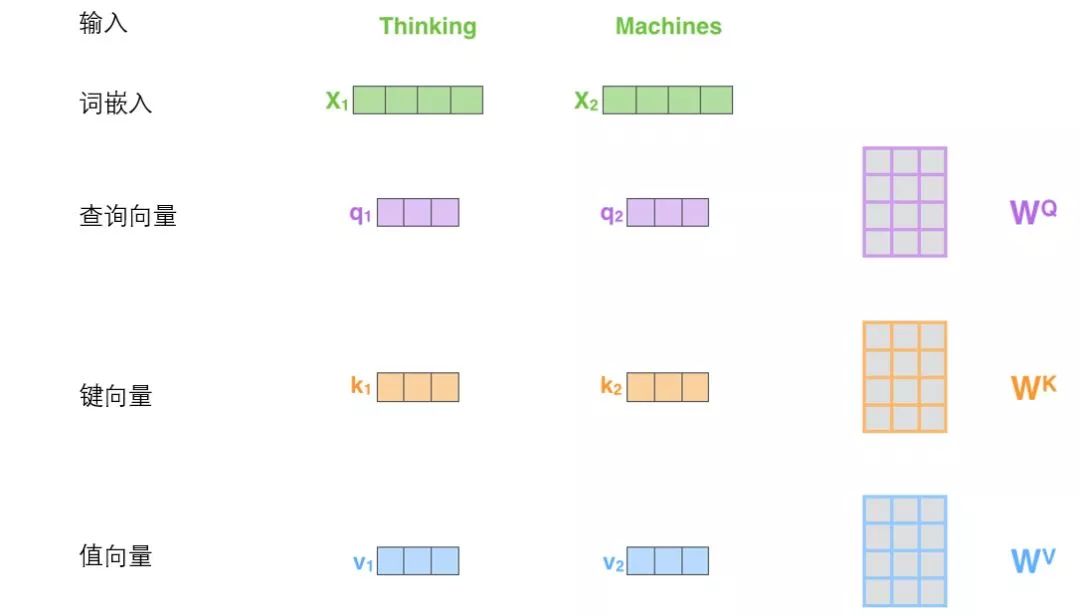
When X1 is multiplied by the weight matrix WQ, we get q1, which is the query vector related to this word. Ultimately, each word in the input sequence creates a query vector, a key vector, and a value vector.
What are Query Vectors, Key Vectors, and Value Vectors?
They are all abstract concepts that help in calculating and understanding the attention mechanism. Please continue reading the content below, and you will know what role each vector plays in calculating the attention mechanism.
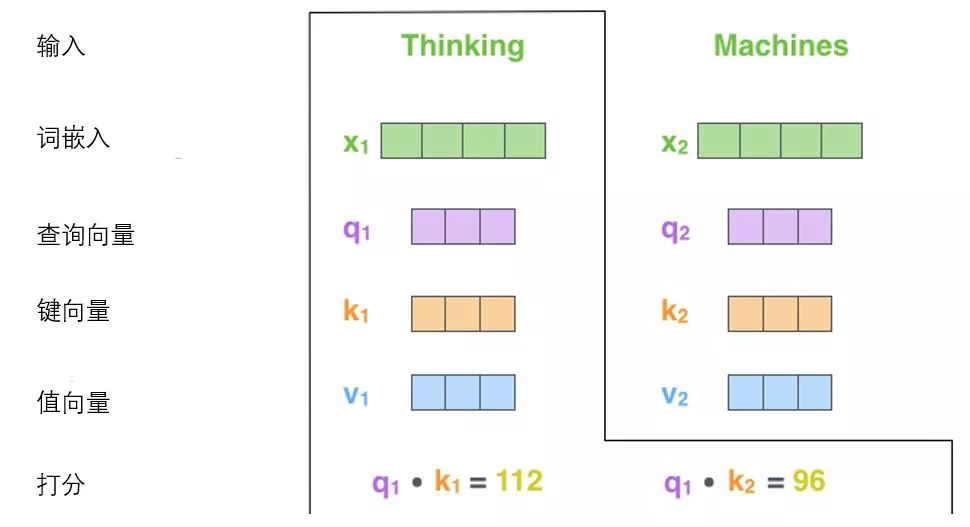
The second step in calculating self-attention is to compute scores. Suppose we are calculating the self-attention vector for the first word “Thinking” in this example; we need to score each word in the input sentence against “Thinking”. These scores determine how much the sentence’s other parts are emphasized in the process of encoding the word “Thinking”.
These scores are calculated by taking the dot product of the key vector of each word (all words in the input sentence) with the query vector of “Thinking”. So if we are processing the self-attention of the first word, the first score is the dot product of q1 and k1, and the second score is the dot product of q1 and k2.
The third and fourth steps involve dividing the scores by 8 (8 is the square root of the dimension of the key vector, which is 64, this makes the gradients more stable. Other values can also be used; 8 is just the default value), and then passing the results through softmax. The role of softmax is to normalize the scores of all words, resulting in positive values that sum to 1.
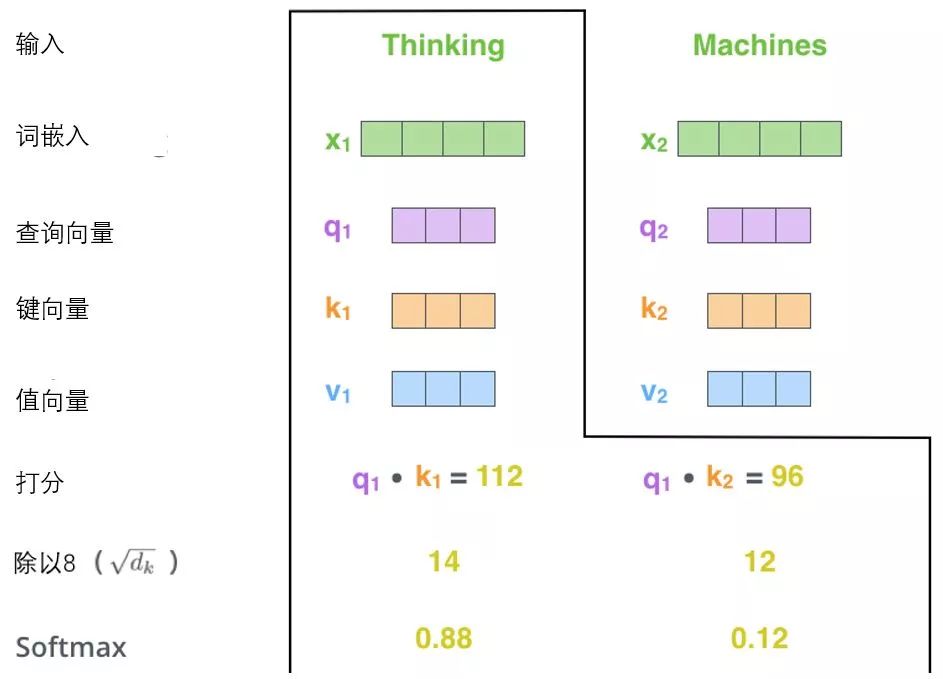
This softmax score determines each word’s contribution to the encoding of the current position (“Thinking”). Clearly, the words that are already in this position will receive the highest softmax scores, but sometimes it can be helpful to pay attention to another word related to the current word.
The fifth step is to multiply each value vector by the softmax score (this is to prepare for summing them later). The intuition here is to focus on semantically relevant words and weaken irrelevant words (for example, multiplying them by a small decimal like 0.001).
The sixth step is to sum the weighted value vectors (note: another interpretation of self-attention is that when encoding a word, it is to sum the representations (value vectors) of all words with weights, where the weights are obtained by the dot product of the representation of the word and the representation of the word being encoded, normalized through softmax), and then we obtain the output of the self-attention layer at that position (in our example, for the first word).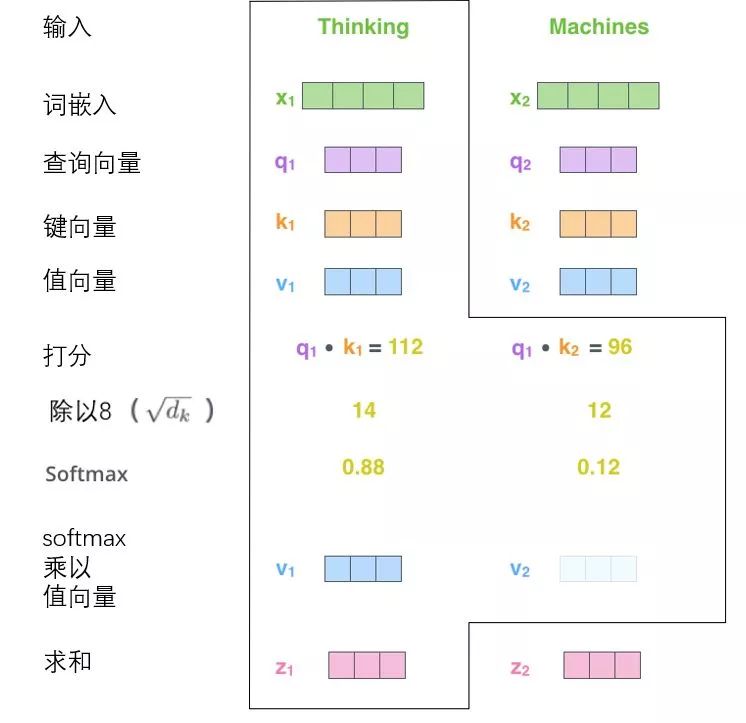
This completes the calculation of self-attention. The resulting vector can then be passed to the feed-forward neural network. However, in practice, these calculations are performed in matrix form for faster computation. Next, let’s see how it is implemented using matrices.
Implementing Self-Attention Mechanism via Matrix Operations
The first step is to calculate the query matrix, key matrix, and value matrix. To do this, we will put the word embeddings of the input sentence into a matrix X and multiply it by our trained weight matrices (WQ, WK, WV).
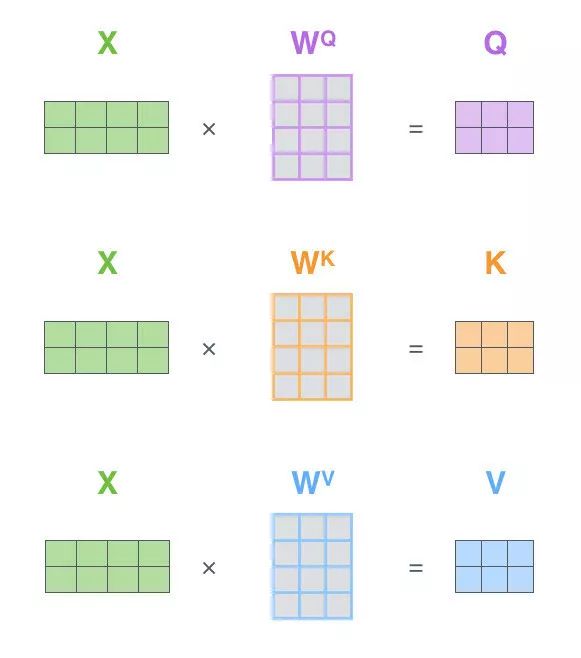
Each row in the x matrix corresponds to a word in the input sentence. We again see the size difference between the word embedding vectors (512, or the 4 boxes in the image) and the q/k/v vectors (64, or the 3 boxes in the image).
Finally, since we are dealing with matrices, we can combine steps 2 to 6 into one formula to compute the output of the self-attention layer.
Matrix Operation Form of Self-Attention
“Battle of the Multi-Headed Beasts”
By introducing a mechanism called “multi-headed attention”, the paper further improves the self-attention layer and enhances its performance in two aspects:
1. It expands the model’s ability to focus on different positions. In the example above, although each encoding has more or less representation in z1, it may be dominated by the actual word itself. If we translate a sentence like “The animal didn’t cross the street because it was too tired”, we would want to know which word “it” refers to, and at this point, the model’s “multi-headed” attention mechanism comes into play.
2. It provides multiple “representation subspaces” for the attention layer. Next, we will see that for the “multi-headed” attention mechanism, we have multiple sets of query/key/value weight matrices (the Transformer uses eight attention heads, so we have eight matrix sets for each encoder/decoder). Each of these sets is randomly initialized, and after training, each set is used to project the input word embeddings (or vectors from lower encoders/decoders) into different representation subspaces.
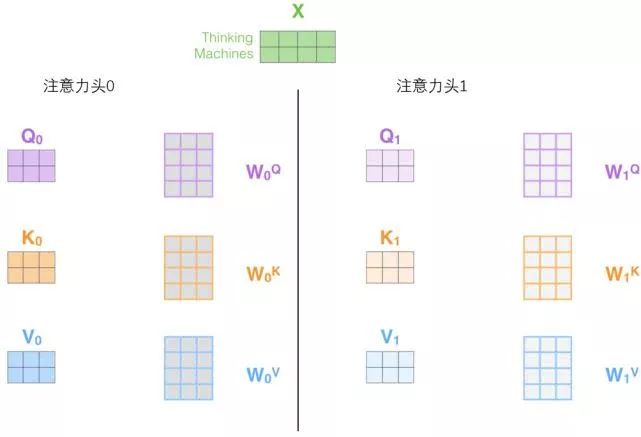
Under the “multi-headed” attention mechanism, we maintain independent query/key/value weight matrices for each head, resulting in different query/key/value matrices. As before, we multiply X by the WQ/WK/WV matrices to produce the query/key/value matrices.
If we perform the same self-attention calculation as above, we will obtain eight different Z matrices with eight different weight matrix operations.
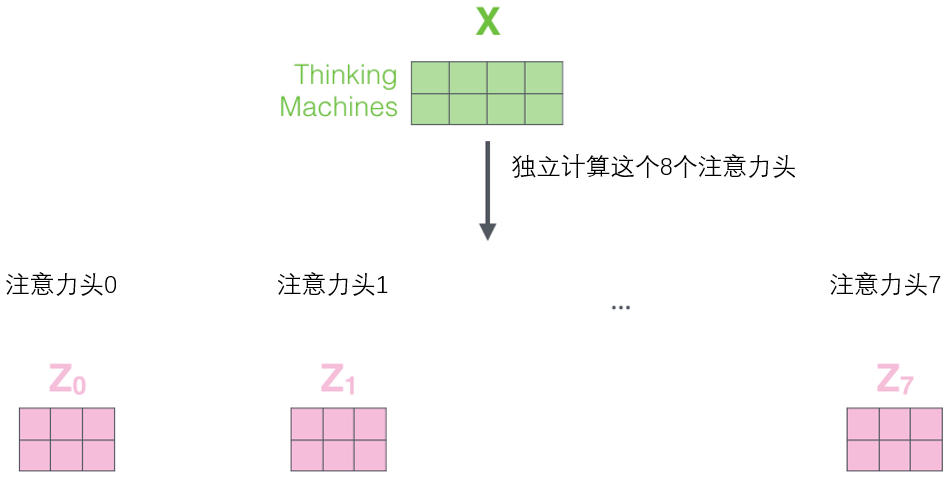
This presents us with a little challenge. The feed-forward layer does not require eight matrices; it only needs one matrix (composed of the representation vectors of each word). So we need a way to compress these eight matrices into one matrix. How do we do this? In fact, we can simply concatenate these matrices together and then multiply them by an additional weight matrix WO.
This is almost all there is to multi-headed self-attention. There are indeed many matrices, and we try to centralize them in one image for clear visibility.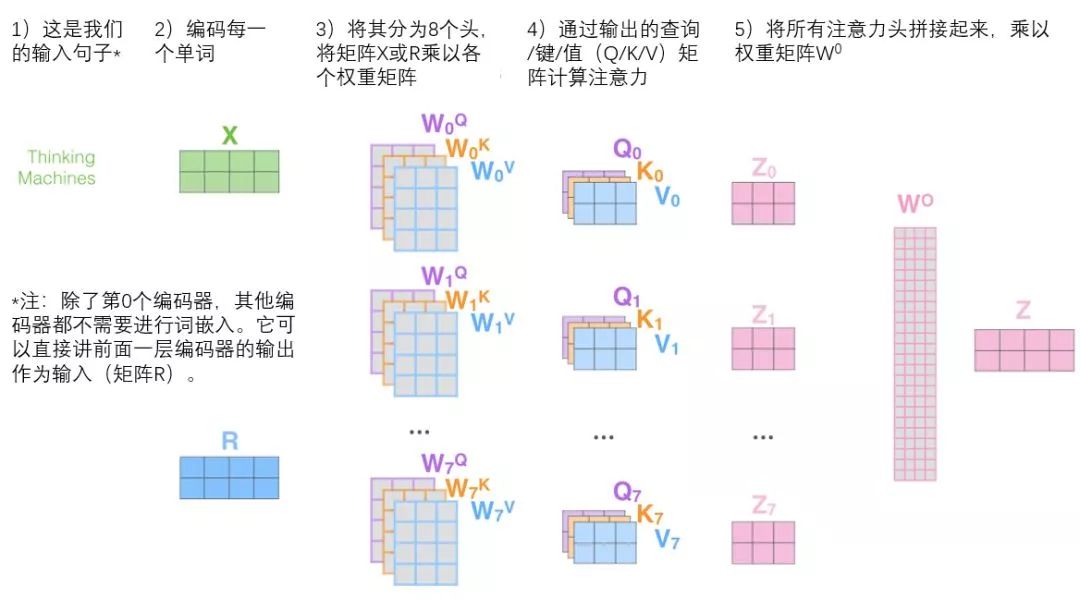
Since we have touched on so many “heads” of the attention mechanism, let’s revisit the previous example to see where the different attention “heads” focus when encoding the word “it”:
When we encode the word “it”, one attention head focuses on “animal”, while another focuses on “tired”. In a sense, the model’s representation of the word “it” is somewhat representative of both “animal” and “tired”.
However, if we add all the attention to the diagram, it becomes harder to explain: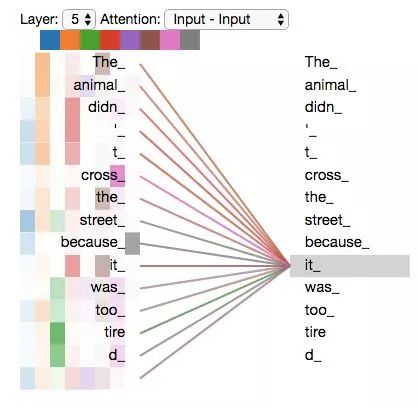
Using Positional Encoding to Represent Sequence Order
So far, our description of the model lacks a method to understand the order of input words.
To solve this problem, the Transformer adds a vector for each input word embedding. These vectors follow a specific pattern learned by the model, which helps determine the position of each word or the distance between different words in the sequence. The intuition here is that adding positional vectors to word embeddings allows them to better express the distance between words in subsequent calculations.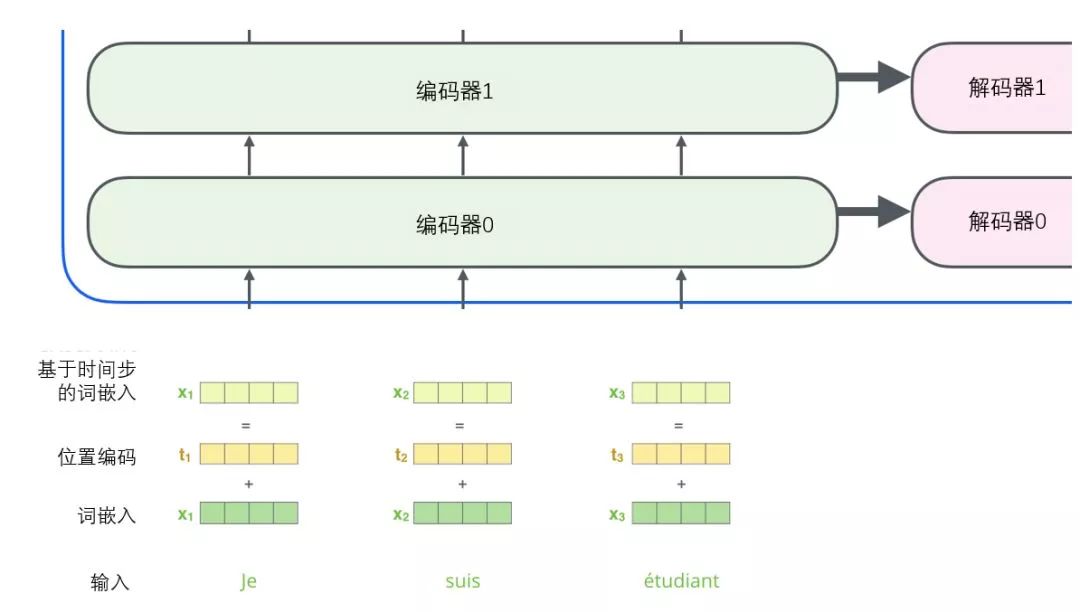
To help the model understand the order of words, we added positional encoding vectors, the values of which follow a specific pattern.
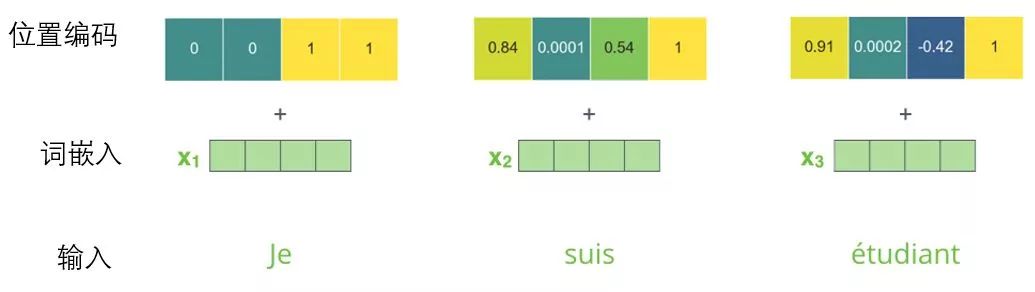
Mini word embedding positional encoding example with a dimension of 4
What would this pattern look like?
In the diagram below, each row corresponds to the positional encoding of a word vector, so the first row corresponds to the first word in the input sequence. Each row contains 512 values, each value between 1 and -1. We have color-coded them to make the pattern visible.
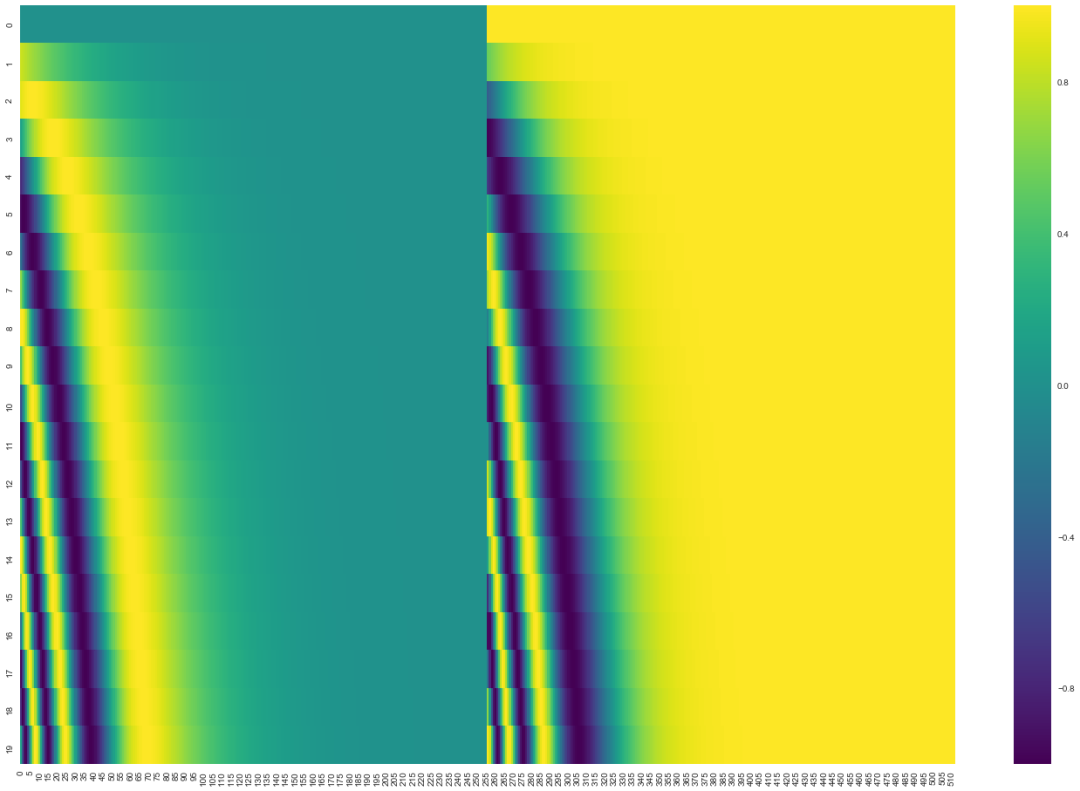
Example of positional encodings for 20 rows (words), with a word embedding size of 512 (columns). You can see that it splits in the middle. This is because the values on the left half are generated by one function (using sine), while the right half is generated by another function (using cosine). They are then concatenated to obtain each positional encoding vector.
The original paper describes the formula for positional encoding (Section 3.5). You can see the code for generating positional encodings in get_timing_signal_1d(). This is not the only possible method for positional encoding. However, its advantage is that it can be extended to unknown sequence lengths (for example, when the trained model needs to translate sentences much longer than those in the training set).
Residual Module
Before we proceed, we need to mention a detail in the encoder architecture: there is a residual connection around each sub-layer (self-attention, feed-forward network) in each encoder, followed by a “layer normalization” step.
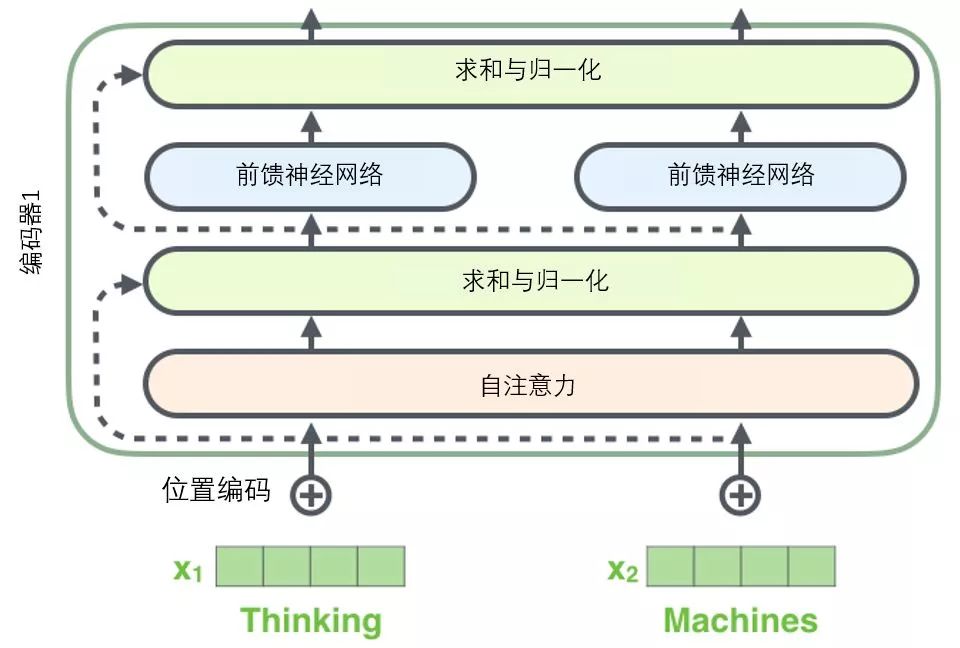
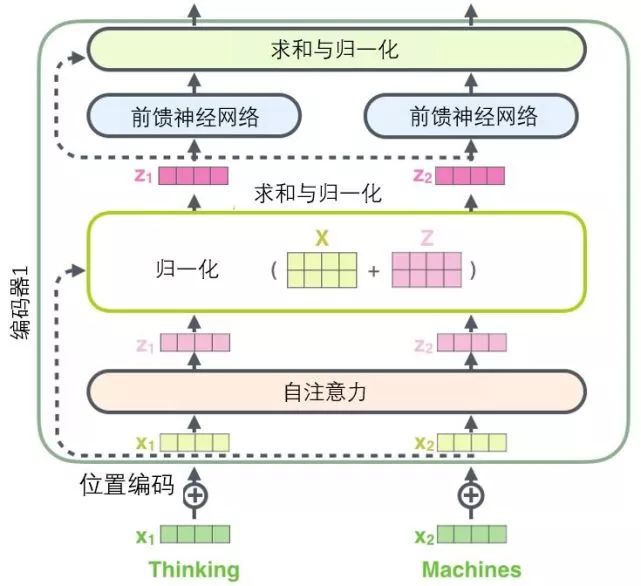
If we visualize these vectors along with the layer normalization operation associated with self-attention, it would look like the diagram below:
The sub-layers of the decoder are also like this. If we imagine a transformer with a 2-layer encoder-decoder structure, it would look like the diagram below:
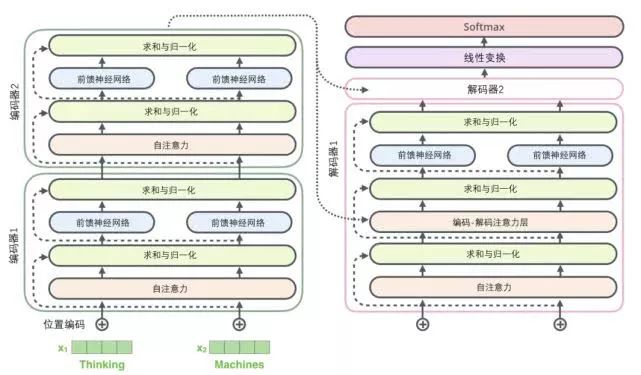Decoder Component
Now that we have discussed most of the concepts of the encoder, we basically know how the decoder works. However, it’s still best to look at the details of the decoder.
The encoder starts working by processing the input sequence. The output of the top encoder is then transformed into a set of attention vectors containing vectors K (key vectors) and V (value vectors). These vectors will be used by each decoder for its own “encoder-decoder attention layer”, which can help the decoder focus on the appropriate positions in the input sequence:
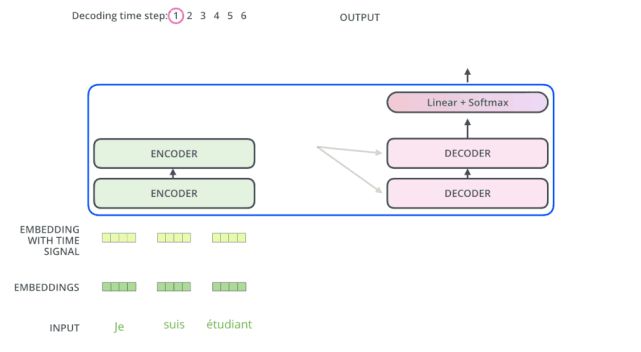
After completing the encoding phase, the decoding phase begins. Each step of the decoding phase outputs an element of the output sequence (in this example, the translated sentence in English).
The subsequent steps repeat this process until reaching a special termination symbol, indicating that the transformer’s decoder has completed its output. The output of each step is provided to the bottom decoder at the next time step, and just as the encoders did before, these decoders will output their decoding results. Additionally, just as we did for the inputs of the encoders, we will embed and add positional encodings to those decoders to represent the position of each word.
The self-attention layers in those decoders exhibit different patterns than in the encoder: in the decoder, the self-attention layer is only allowed to process earlier positions in the output sequence. Before the softmax step, it masks the later positions (setting them to -inf).
The “encoder-decoder attention layer” works similarly to the multi-headed self-attention layer, except that it creates the query matrix from the layer below it and obtains the key/value matrices from the encoder’s output.
Final Linear Transformation and Softmax Layer
The decoder component finally outputs a real-valued vector. How do we turn floating-point numbers into words? This is what the linear transformation layer is supposed to do, followed by the Softmax layer.
The linear transformation layer is a simple fully connected neural network that projects the vector generated by the decoder component into a much larger vector called logits.
Let’s assume our model has learned 10,000 different English words from the training set (our model’s “output vocabulary”). Therefore, the logits vector is a vector of length 10,000 cells – each cell corresponds to a score for a specific word.
The subsequent Softmax layer then converts those scores into probabilities (all positive numbers, capped at 1.0). The cell with the highest probability is selected, and the corresponding word is output as the output for that time step.
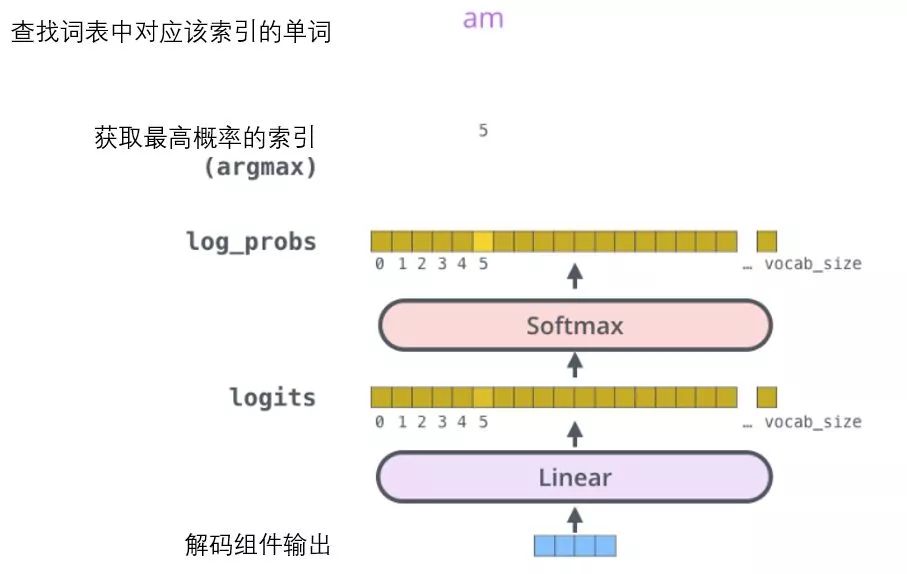This image starts with the output vector generated by the decoder component. It then transforms it into an output word.
Training Summary
Now that we have gone through the complete forward propagation process of the transformer, we can intuitively feel its training process.
During training, an untrained model goes through exactly the same forward propagation. However, since we are training it with a labeled training set, we can compare its output with the true output.
To visualize this process, let’s assume our output vocabulary contains only six words: “a”, “am”, “i”, “thanks”, “student” and “”(the abbreviation for end of sentence).
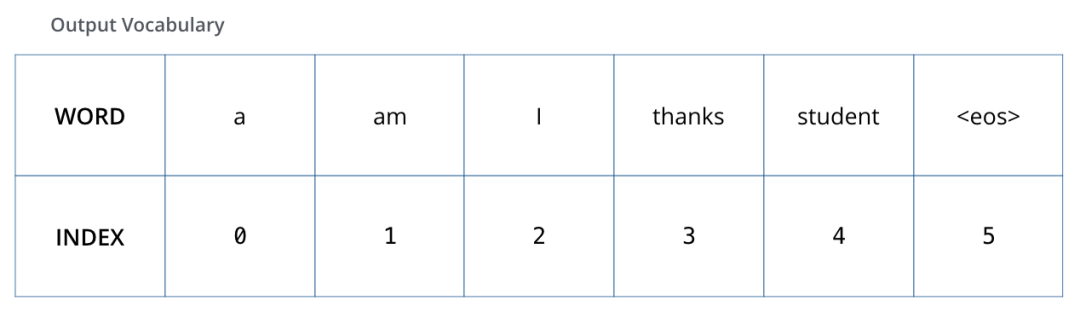
The output vocabulary of our model was set during the preprocessing process before training.
Once we define our output vocabulary, we can use a vector of the same width to represent each word in our vocabulary. This is also known as a one-hot encoding. So we can use the following vector to represent the word “am”:
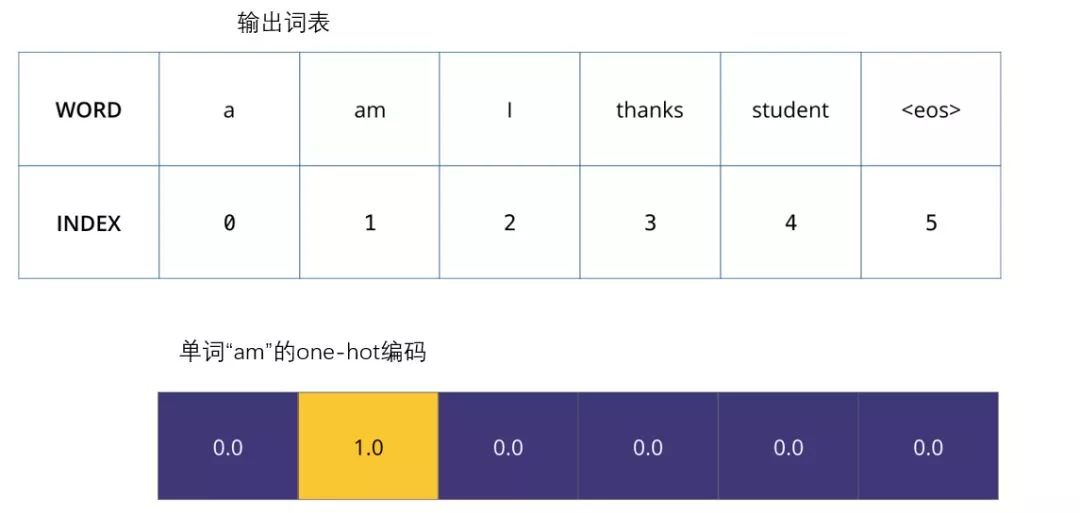
Example: One-hot encoding of our output vocabulary
Next, we discuss the model’s loss function – this is the standard we use to optimize during training. It allows us to train a model that produces results as accurately as possible.
Loss Function
For example, we are training the model, and now it’s the first step, a simple example – translating “merci” to “thanks”.
This means we want an output that represents the probability distribution of the word “thanks”. However, since this model is not yet trained, it is unlikely to produce this result now.
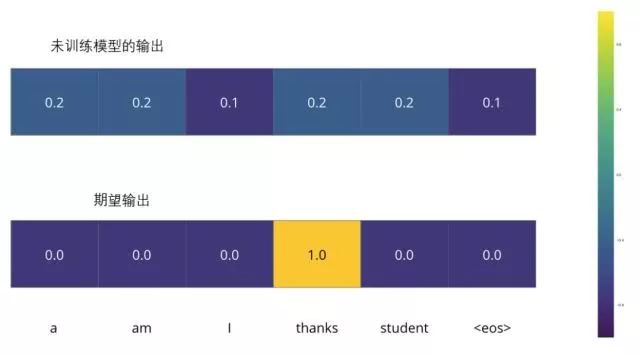
Since the parameters (weights) of the model are randomly generated, the (untrained) model produces a probability distribution that assigns random values to each cell/word. We can compare this with the true output and use the backpropagation algorithm to slightly adjust all the model’s weights to generate outputs that are closer to the result.
How would you compare two probability distributions? We can simply subtract one from the other. For more details, refer to cross-entropy and KL divergence.
However, note that this is an oversimplified example. A more realistic situation is processing a sentence. For example, inputting “je suis étudiant” and expecting the output to be “i am a student”. We hope that our model can successfully output the probability distributions in these cases:
Each probability distribution is represented by a vector with a width equal to the size of the vocabulary (in our example, it is 6, but in reality, it is usually 3000 or 10,000).
The first probability distribution has the highest probability in the cell associated with “i”
The second probability distribution has the highest probability in the cell associated with “am”
And so on, the fifth output’s distribution indicates the highest probability in the cell associated with “”
After sufficient training on a large enough dataset, we hope that the probability distribution output by the model looks like this: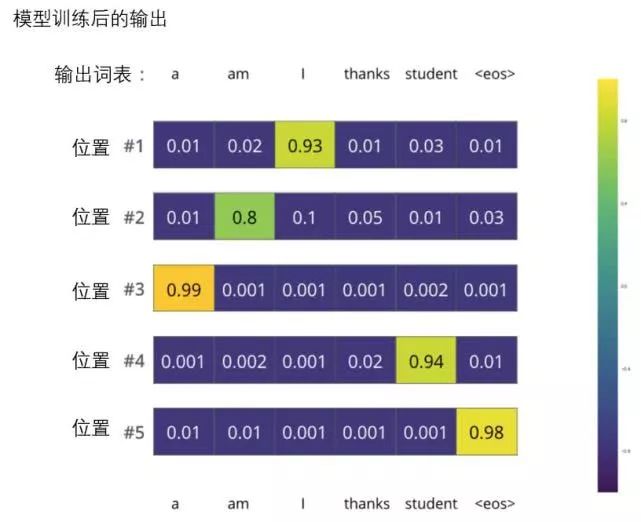
We expect that after training, the model will output the correct translation. Of course, if this sentence comes entirely from the training set, it is not a very good evaluation metric. Note that each position (word) receives a bit of probability, even if it is unlikely to be the output at that time step – this is a useful property of softmax that helps the model train.
Because this model produces one output at a time, let’s assume this model only selects the word with the highest probability and discards the rest. This is one method (called greedy decoding). Another way to complete this task is to keep the two words with the highest probabilities (for example, I and a), and then run the model twice for the next step: once assuming the first position outputs the word “I” and once assuming the first position outputs the word “me”, and whichever version produces the least error retains the result with the highest probability. Then we repeat this step for the second and third positions. This method is called beam search (in our example, the beam width is 2 since we retained 2 results from the first and second positions), and it also returns two results from the beams (top_beams is also 2). These are parameters that can be set in advance.
Going Further
I hope that through the above text, I have helped you understand the main concepts of the Transformer. If you want to delve deeper into this field, I recommend taking the following steps: read Attention Is All You Need, the Transformer blog, and the Tensor2Tensor announcement, and check out Łukasz Kaiser’s introduction to understand the model and its details.
Editor: Yu Tengkai
Proofreader: Lin Yilin
