
Participants of the 1956 Dartmouth Conference. Left 2: Rochester, Left 3: Solomonoff, Left 4: Minsky, Right 2: McCarthy, Right 1: Shannon
Introduction:
The secret to the success of OpenAI’s GPT series, the most popular large model company, lies in next token prediction (essentially: predicting the next word), which is mathematically based on Solomonoff’s induction.
This method is the theoretical cornerstone of large language models, revealing the core mechanism of GPT. As this theory marks its 60th anniversary, this article summarizes the importance of Solomonoff’s induction and its unique contributions alongside other scholars. It also discusses the latest developments of this theory, its applications in AI, and its philosophical implications. Readers interested in AI should not miss this.

Solomonoff (July 25, 1926 – December 7, 2009)
The development of science often involves the intertwining of theory and practice. The history of Natural Language Processing (NLP) is convoluted, especially in the development of large language models, which involves both theory and practice, influenced by commercial factors. Although engineers have tried to find its mathematical foundation, true theoretical foundations are rarely discovered. In fact, mathematician Solomonoff laid the mathematical groundwork for large models as early as the 1960s, and his theories still have guiding significance today.
In 1956, McCarthy and Minsky, supported by Shannon at Bell Labs and Rochester at IBM, held the Dartmouth Summer Research Project on Artificial Intelligence, marking the birth of artificial intelligence as an independent discipline. Solomonoff was the most serious participant at this conference, staying at Dartmouth for the entire summer. His academic career was influenced by philosopher Carnap, focusing on inductive reasoning.
The founders of neural networks, Pitts, and AI pioneer Simon, also benefited from Carnap’s ideas. After meeting Minsky and McCarthy, Solomonoff began to focus on the study of logic and recursive functions. Recursive functions gradually evolved into computability theory, which in turn gave rise to computational complexity. Minsky’s textbook on computational theory had a significant impact on the early development of computational theory, and his viewpoint that “AI gave birth to computational theory” holds some truth. In 1953, while working at Bell Labs, McCarthy and Minsky, around information theory expert Shannon, researched the theory of Turing machines and the foundations of intelligent activities. At that time, the older Wiener released his new book “Cybernetics”, but Shannon and McCarthy did not agree with it. McCarthy suggested to Shannon to publish a collection, inviting leading researchers of the time to write articles, which was published in 1956 under the title “Studies in Automata”. McCarthy published a short article in it discussing the inverse function problem of Turing machines, namely how to infer the input of a Turing machine by observing its output. McCarthy believed that all mathematical problems could be solved by inverting Turing machines. During the Dartmouth conference, McCarthy had a long discussion with Solomonoff, who transformed McCarthy’s problem into the problem of seeking the subsequent sequence given an initial segment. McCarthy initially did not understand this idea but later realized its importance. Their so-called “sequence continuation”, “next word”, or “next symbol” is now known as “next token”.

2006 Dartmouth Conference 50th Anniversary. Left 2: McCarthy, Left 3: Minsky, Right 1: Solomonoff
This statement originates from a 1913 article by French mathematician Borel, who considered whether a monkey randomly typing on a typewriter could type out “Hamlet”, pointing out that while the probability is low, it is not zero, known as the “infinite monkey theorem”. Argentine writer Borges imagined a perfect library in his works, containing all possible books. Today’s large model training also strives in this direction, attempting to exhaust all human knowledge. Borges’ starting point is rationalism, while the random monkey represents empiricism, but both can be unified by McCarthy’s inversion into the enumeration process of Turing machines. Turing’s 1948 article “Intelligent Machines” mentioned methods of machine learning, stating that all learning can be reduced to an enumeration process, but this process is non-terminating or non-computable.

After discussions with McCarthy, Solomonoff completed a memorandum on inductive reasoning titled “An Inductive Inference Machine” before the end of the Dartmouth conference, dated August 14, 1956. He circulated this typed manuscript among the attendees and sent an improved version to Simon at Carnegie Tech at the end of 1956.
Solomonoff’s work was first publicly presented at the 1960 conference on “Brain Systems and Computers” and was widely disseminated through reports by Zator Company and the US Air Force AFOSR the same year. In 1961, Minsky mentioned this work in his article “Steps Toward Artificial Intelligence”. After further revisions, Solomonoff formally published it under the title “Formal Theory of Inductive Inference” in the journal “Information and Control” in 1964. The article was too long and was divided into two parts, with the first half discussing theory and the second half discussing examples.
Solomonoff’s induction is defined as: given a sequence (x1, x2, …, xn), predict xn+1. Inductive reasoning seeks the smallest Turing machine to model (x1, x2, …, xn) to accurately predict the subsequent sequence. The description length of the sequence is the size of the Turing machine, consistent with what McCarthy initially realized as “effectiveness”. For example, the description length of the sequence (1, 1, 1,…) is O(log(n)).
Supervised learning can be seen as a special case of self-supervised learning. Supervised learning gives pairs of sequences (x1,c1), (x2,c2), …,(xn,cn) and xn+1, predicting cn+1. The learning process is to find a fitting function c=f(x). This type of problem can easily be transformed into self-supervised learning: given the sequence (x1,c1,x2,c2,…,xn,cn,xn+1), predict cn+1.
McCarthy described this as the problem of “betting on the next character”, which is the core mechanism of large language models like GPT: next token prediction. A Turing machine that summarizes known data is a large model. For the same dataset, the fewer parameters a large model has, the better it is expected to cover the dataset, that is, to find the most economical Turing machine. Learning can be seen as compression, and the relationship between the number of parameters and the number of tokens can be studied this way. Solomonoff’s induction may not terminate, hence approximate algorithms are used, relaxing the constraints on the “minimality” and prediction accuracy of Turing machines. He derived the prior probability distribution of sequences using Bayes’ theorem. Neural networks, as universal approximators, are good candidates for realizing Solomonoff’s induction, which is also the approach of today’s large models. Solomonoff was interested in the problem of generating sentence syntax and, inspired by Chomsky, generalized grammar into probabilistic grammar. His “inductive inference machine” could learn grammar from input text, known as “grammar discovery”. Chomsky’s innate grammar is similar to Solomonoff’s prior probability distribution, but the two standpoints differ. According to the Church-Turing thesis, the distinction between the two is merely rhetorical. In Solomonoff’s prior probability distribution, the confidence of a program decreases exponentially with length, consistent with Occam’s razor principle. This is a wonderful formula:
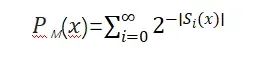
His life was not affluent; he spent most of his time conducting government research at his consulting firm, Oxbridge, which had only him. His academic autobiography, “Discovery of Algorithmic Probability Theory”, was published in 1997 and has been revised multiple times. The latest version is included in the collection “Randomness Through Computation: Some Answers, More Questions”.

Soviet mathematician Kolmogorov made profound contributions to traditional mathematics and had a significant impact on computer science and information theory. In the 1950s, he keenly recognized the importance of information theory while being skeptical of cybernetics. Kolmogorov conducted in-depth research in probability theory, founded the quarterly journal “Problems of Information Transmission”, proposed a quantitative definition of information, and divided it into three foundations: frequency, combinatorics, and algorithms. He advocated that information theory logically precedes probability theory, with algorithms being the most solid. Kolmogorov’s complexity theory is defined as the length of the shortest program that generates a string, and his articles are concise yet profound. Although some of his theories require further refinement by later generations, his work remains of great significance. Kolmogorov complexity is independent of the representation of programs; different program representations such as C, Java, Python, or Turing machine code differ in their shortest descriptions only by a constant, a property known as the Kolmogorov thesis. Kolmogorov complexity is considered more reliable than Shannon entropy because the Kolmogorov complexity of a graph is invariant, while structural entropy varies with different representations of the graph. Kolmogorov cited Solomonoff’s work, which elevated the latter’s reputation in the Soviet Union beyond that in the West. Kolmogorov complexity is also known as Solomonoff complexity or Solomonoff-Kolmogorov-Chaitin complexity; to avoid ambiguity, this article adopts the term “Kolmogorov complexity”. Influenced by Kolmogorov, this field is also referred to as algorithmic probability theory or algorithmic information theory. At Royal Holloway, University of London, Soviet scholars established a machine learning research center and established the Kolmogorov Medal, with Solomonoff as the first recipient; the most recent recipient is Vladimir Vapnik. Solomonoff also served as a part-time professor at that institution.


Solomonoff (left) with Chaitin, 2003
Greg Chaitin, a Jewish American theoretical computer scientist born in Argentina (1947-), excelled in high school and published articles on automata clock synchronization. He returned to Argentina with his parents before graduating from college, found a programmer job at an IBM subsidiary, and studied Gödel’s incompleteness theorem. At 19, he independently reinvented Solomonoff’s induction and the idea of Kolmogorov information and published it in the journal of the American Computer Society.
Chaitin’s research is based on Berry’s paradox; he used the LISP functional programming language to avoid confusion. He proved that Kolmogorov complexity is non-computable, calling it “incompleteness”. In 1974, Chaitin returned to the US and worked at the IBM TJ Watson Research Center, where he presented a version of the incompleteness theorem obtained using Berry’s paradox to Gödel, who expressed indifference, but Chaitin still believed his proof provided a new informational perspective on incompleteness. Chaitin sent his article in IEEE Transactions on Information Theory to Gödel and scheduled a meeting, but Gödel canceled due to health issues and fear of snow, which Chaitin deeply regretted. He was invited to speak at the University of Vienna in 1991 and was praised as “more Gödel than Gödel”. In his later years, Chaitin developed a strong interest in biology and published popular science works such as “Proving Darwin”, expressing dissatisfaction with the lack of theoretical foundations in biology and proposing to explain evolution using algorithmic information theory, termed “meta-biology”, with insights found in genetic algorithms and programming.

Soviet mathematician Leonid Levin independently proposed NP-completeness in 1972 and proved several equivalent problems, with his article published in the journal founded by Kolmogorov. Although he did not obtain a doctorate due to political issues, he later earned his Ph.D. at MIT and taught at Boston University until retirement. His contributions are widely recognized; the Cook theorem in computational theory textbooks has been renamed the Cook-Levin theorem. In 2012, he received the Gödel Prize for considering the impact on the entire discipline.
Levin’s articles are usually very brief; his algorithmic average complexity analysis, initiated in 1986, is only two pages long. Although Levin tends to believe that P=NP, this is a minority view in academia.
In a 1973 paper, Levin presented two theorems, with theorem 1 regarding NP-completeness, while theorem 2 was ignored at the time. Theorem 1 was not proven in detail, and theorem 2 was not even stated. Levin proposed a universal search process related to McCarthy’s problem, which Solomonoff had already researched for 20 years.
Upon learning of Levin’s situation in the Soviet Union, Solomonoff reached out to American schools and scholars to help Levin. He wrote a report on his academic discussions with Levin, providing a proof for theorem 2 of Levin-1973, and named Levin’s universal search process as L-search.
Levin’s L-search, based on Kolmogorov complexity, adds a time constraint and can be defined as:
Kt(x) = min{ℓ(p) + log(time(p)): U(p) = x}
Thus, Levin’s complexity is computable, meaning that if the inverse function exists, it can always be found through Levin’s universal search process. This aligns with Solomonoff’s earlier convergence theorem.

Second page of Levin’s 1973 paper. Acknowledgments precede the references, and the statement of theorem 2 comes before the acknowledgments.

Physicist Charles Bennett (1943-) is famous for quantum computing and is the first B in the quantum key distribution protocol BB84. He has made outstanding contributions to algorithmic information theory, introducing the concept of logical depth in 1988 (see Bennett-1988), defined as:
LD(x) = min{T(p): ℓ(p) =p*+s ∧U(p) = x}
That is, the time required for the near-shortest program to output x. Here, p* is Kolmogorov complexity, and ℓ(p) is the length of the near-shortest program. It can be seen that logical depth further relaxes the requirements of Kolmogorov complexity on the shortest length of programs.
If we consider induction as compression, logical depth considers the time cost of decompression. Logical depth allows us to consider the relationship between time and space. Intuitively, we might think that time is more “expensive” than space, but currently, in computational theory, we do not know whether the class P of polynomial time is equal to the class PSPACE of polynomial space; of course, NP is a subset of PSPACE, but it is unknown whether it is a proper subset. If P≠PSPACE, there must exist strings computable in PSPACE whose logical depth exceeds polynomial time. Compression primarily considers spatial costs, but decompression has time costs.
The compression time of large models is the training time, Kolmogorov complexity represents the number of parameters, and logical depth corresponds to the shortest “inference” time. The term “inference” is more appropriate here because it is statistical in nature, differing from the logical meaning of “reasoning”. There is also logical meaning of “reasoning” in large models, such as CoT, but textbooks on machine theorem proving often do not distinguish between inference and reasoning. If the logical and statistical factions of artificial intelligence both spoke Chinese, they might not argue.


Li Ming and his wife with Solomonoff
Theoretical computer scientists such as Li Ming have made significant contributions to the study of Solomonoff-Kolmogorov-Chaitin complexity. Their co-authored book “Kolmogorov Complexity and Its Applications” is an authoritative reference in this field, now in its 4th edition. Marcus Hutter shifted from theoretical physics to general artificial intelligence and proposed a theoretical framework for AGI based on reinforcement learning, whose mathematical tools are Solomonoff’s induction.
The success of OpenAI’s ChatGPT, often attributed to the underlying neural network architecture Transformer, may actually hinge on GPT’s next token prediction (Solomonoff induction). Currently, theoretical research on large models lags behind engineering practices. The Solomonoff-Kolmogorov-Chaitin theory posits that learning can be viewed as compression, a process of summarizing data or transitioning from particulars to universals. The Hutter Prize established by Hutter rewards the best lossless compression work, and his article “Language Modeling is Compression” indicates that large language models perform better in lossless compression than Huffman coding-based compression algorithms.
Kolmogorov and Chaitin’s starting points are information expression and transmission, also compression. These views have sparked enthusiastic discussions among engineers, providing new perspectives for the development of large language models.

Solomonoff’s induction is described as follows:
-
Input observation data.
-
Propose a new hypothesis (Turing machine) to explain the data.
-
Input new data to test the hypothesis.
-
If the data falsifies the hypothesis, return to step 2.
-
If the data confirms the hypothesis, continue accepting the hypothesis and return to step 3.
This method is similar to Peirce’s pragmatism, emphasizing the discovery of the unknown from the known. Peirce believed that rationalism and empiricism are not entirely opposed; when a new hypothesis is established and begins to explain a large amount of data, the system resembles a rationalist; when new data falsifies an old hypothesis, the system resembles an empiricist.
Solomonoff’s induction can also explain Popper’s theory of falsification. He believed that falsification is easier than confirmation because it is easier to say that something is wrong than to say that something is right. This is similar to Peirce’s concept of “falsifiability”. Additionally, statistician George Box stated that all models are wrong, but some are useful for prediction.
Kuhn’s theory of scientific revolutions is also a special case of Solomonoff’s induction. Occam’s razor principle states that under the premise of similar explanatory power, the smaller the model, the better. In Solomonoff’s theory, the minimal model covering all data is the shortest program or Turing machine. A scientific revolution occurs when there is a significant difference between old and new models. The new model may be more complex and logically deeper than the old model.
Finally, Solomonoff’s induction can explain theories about consciousness.

Aristotle pointed out in “Metaphysics” that “the pursuit of knowledge is human nature”. He described the process of human knowledge from experience to technology and then to science. Regarding the concepts of “non-computable” or “non-terminating”, they may symbolize the hope left by God for humanity. Within Solomonoff’s theoretical framework, the progress of knowledge is viewed as “incremental learning”. In-depth research into Solomonoff’s induction and Kolmogorov complexity is expected to provide a new theoretical foundation for machine learning. Currently, genetic algorithms, genetic programming, and reinforcement learning can all find computational theory support within Solomonoff’s induction framework.
Aristotle’s view can also be borrowed as “compression is human nature”. Hume believed that although induction cannot confirm, it is crucial for human nature. Under this view, compression can be seen as the essence of humanity. Experience originates from sensation, and modeling experience data is driven by economic considerations, while modeling itself is compression, a process accomplished by Turing machines. Solomonoff’s induction can be regarded as a first principle in this sense. The evolutionary process can also be seen as compression, with survival of the fittest interpreted as “the most compressible survive”. Compression reflects the manifestation of physical laws in the world of information. Descartes’ “I think, therefore I am” can be strictly expressed as “I compress, therefore I am”.
