A Detailed Guide to Self-Attention Mechanism

Self-Attention is the core idea of Transformer. Recently, I re-read the paper and gained some new insights. Thus, I wrote this article to share my thoughts with readers.

When I first encountered Self-Attention, the most confusing part for me was the three matrices Q, K, and V, as well as the commonly mentioned Query vector, etc. The reason for this confusion was the complex high-dimensional matrix operations, which made it difficult to truly understand the core meaning of matrix operations. Therefore, before starting this article, I will first summarize some basic knowledge, which will be revisited in the context of how these ideas manifest in the model.

Some Basic Knowledge

1. What is the inner product of vectors, how is it calculated, and most importantly, what is its geometric meaning?
2. What is the significance of multiplying a matrix by its own transpose?

1. Key-Value Attention

In this section, we will first analyze the core part of the Transformer. We will start from the formula and illustrate each step with diagrams to facilitate readers’ understanding.

The core formula for key-value attention is shown in the figure below. This formula contains many points, which we will discuss one by one. Please follow my thought process, starting from the most essential part, and the finer details will become clear.

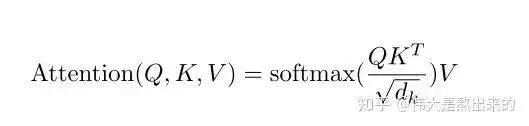
If the formula above is difficult to understand, can readers grasp the meaning of the formula below?

Let’s set aside the matrices Q, K, and V for now. The original form of self-attention looks like this. So what does this formula mean?

Let’s discuss it step by step.

What does it represent?

What result does multiplying a matrix by its own transpose yield, and what is its significance?

We know that a matrix can be seen as composed of several vectors. The operation of a matrix multiplied by its transpose can be viewed as each of these vectors calculating the inner product with other vectors. (At this point, I recall the mnemonic for matrix multiplication: first row multiplied by the first column, first row multiplied by the second column… hmm, the first row becomes the first column after transposition, right? This is calculating the inner product of the first row vector with itself, the first row multiplied by the second column calculates the inner product of the first row vector with the second row vector, and so on.)

Reflecting on the question posed at the beginning of the article: what is the geometric meaning of the inner product of vectors?

Answer: It represents the angle between two vectors and the projection of one vector onto another.

Keep this knowledge point in mind as we move into a super detailed example:

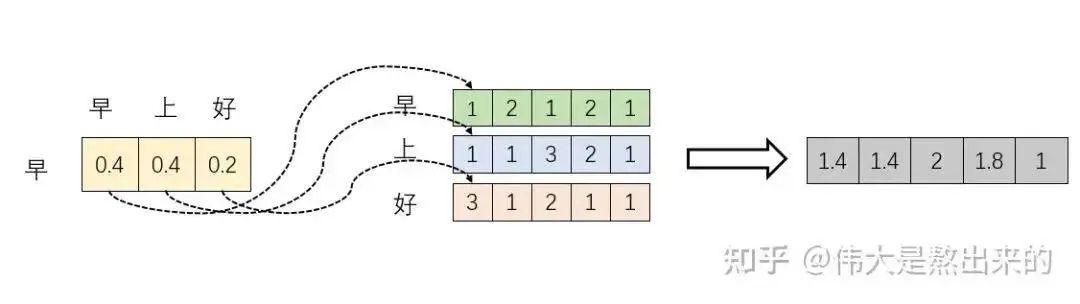
Let’s assume that is a two-dimensional matrix, and is a row vector (many textbooks assume vectors are column vectors; for convenience, please understand that I am using a row vector). The corresponding illustration below represents the embedding result of the character “早” (zao), and so forth.

The following operation simulates a process, i.e., . Let’s examine what this result means.

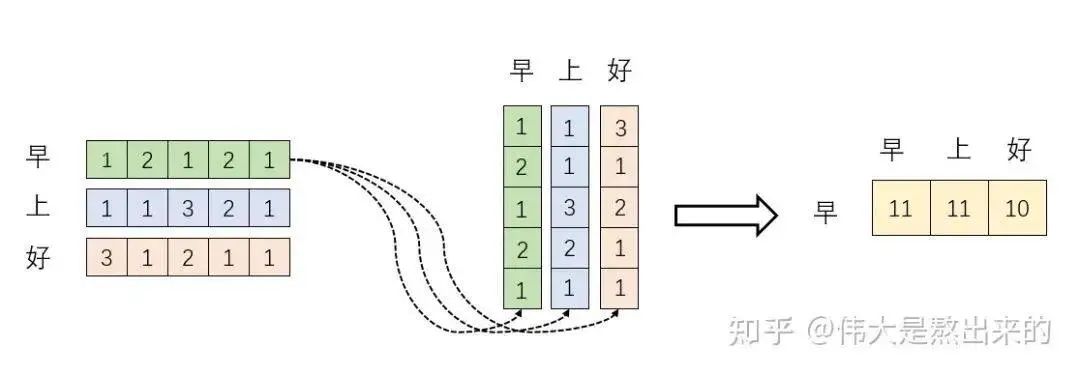
First, the row vector calculates the inner product with itself and the other two row vectors (“早” with “上” and “好”). This results in a new vector. Remember the earlier mentioned inner product of vectors represents the angle between two vectors and the projection of one vector onto another. So what does the new vector signify? It represents the projections of the row vector onto itself and the other two row vectors. We contemplate, what does it mean if the projection value is large? What if it’s small?

A large projection value indicates a high degree of correlation between the two vectors.

If the angle between two vectors is ninety degrees, then these two vectors are linearly independent and have no correlation!

Furthermore, this vector is a word vector, which is a numerical mapping of words in high-dimensional space. A high degree of correlation between word vectors indicates that, to some extent (not completely), when focusing on word A, more attention should be given to word B.

The figure above shows the result of a row vector operation. So what is the significance of the matrix ?

Matrix is a square matrix. Understanding from the perspective of row vectors, it stores the results of inner product operations between each vector with itself and other vectors.

At this point, we understand the meaning of in the formula . Let’s continue and explore the significance of Softmax. Please see the figure below.

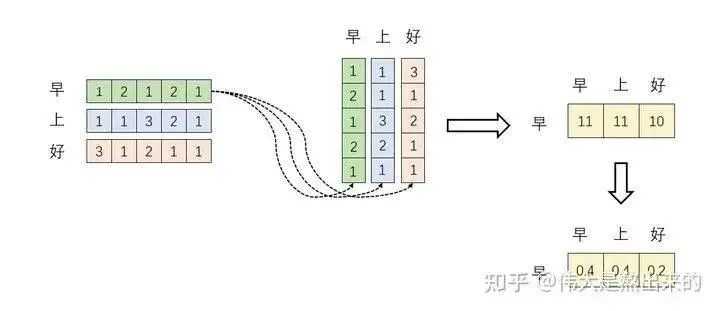
Reflecting on the Softmax formula, what is the significance of the Softmax operation?

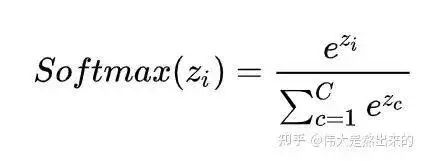
Answer: Normalization.

Combining with the previous figure, after Softmax, the sum of these numbers equals 1. Now, let’s think: what is the core of the attention mechanism?

Weighted summation.

So where do the weights come from? They are the numbers after normalization. When we focus on the character “早”, we should allocate 0.4 of our attention to itself, 0.4 to “上”, and 0.2 to “好”. Of course, in our Transformer, this corresponds to vector operations, but that’s a later topic.

At this point, do we feel somewhat familiar with this concept? The heatmap in Python, does the matrix not also store the results of similarity?

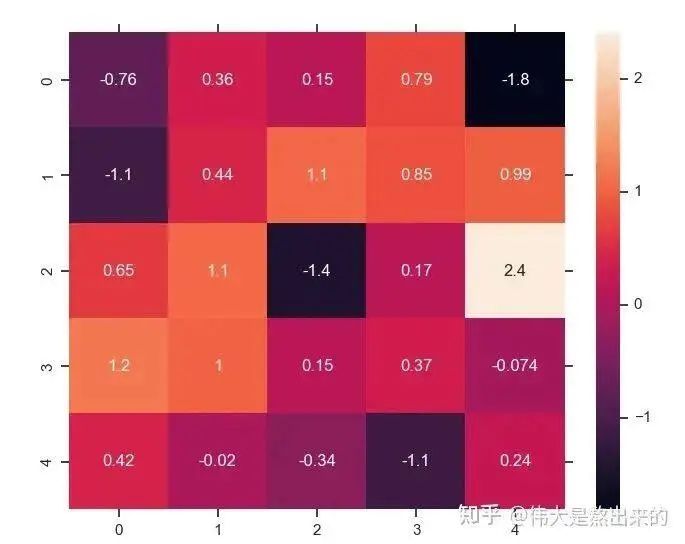
It seems we have cleared some fog; we have already understood half of the formula . What is the significance of the last X? What does the complete formula represent? Let’s continue with our calculations. Please see the figure below.

Let’s take one row vector from as an example. What does multiplying this row vector by a column vector from represent?

In the figure above, multiplying the row vector by the first column vector from yields a new row vector, which has the same dimensions as .

In this new vector, each dimension’s value is obtained by weighted summation of the values of the three word vectors in that dimension. This new row vector is the representation of the word vector for “早” after the attention mechanism’s weighted summation.

A more illustrative figure is as follows; the color depth in the right half of the figure actually represents the values in the yellow vector from the previous figure, indicating the relevance between words (remember, the essence of relevance is measured by the inner product of vectors)!

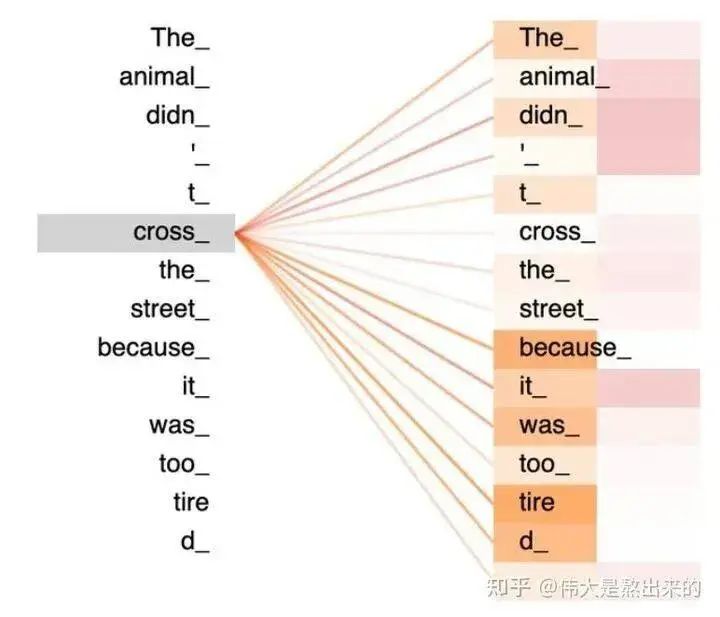
If you have persisted in reading this far, I believe you now have a deeper understanding of the formula .

Next, we will explain some finer details of the original formula.

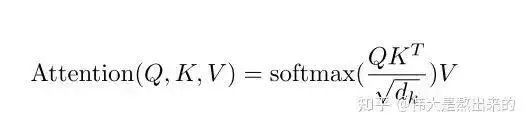
2. Q K V Matrices

In our previous examples, we did not mention Q, K, and V because they are not the most essential content in the formula.

What exactly are Q, K, and V? Let’s look at the figure below.

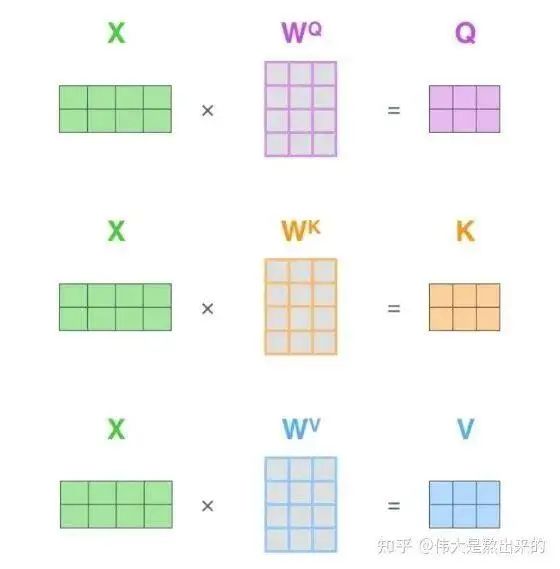
Actually, many articles refer to the Q, K, and V matrices and query vectors, which originate from the product of and the matrix. Essentially, they are linear transformations of .

Why not directly use but instead perform linear transformations on it?

Of course, this is to enhance the model’s fitting ability; the matrices can be trained and serve as a buffering effect.

If you truly understand the content of the previous sections and the meaning of the matrix , I believe you will also grasp the meaning of terms like query vectors.

3. The Significance of

Assuming the mean of the elements in is 0 and the variance is 1, then the mean of the elements in is 0, and the variance is d. When d becomes very large, the variance of the elements in will also become very large. If the variance of the elements in is large, the distribution of will tend to be steep (a large variance in the distribution indicates that the distribution is concentrated in regions of large absolute values). In summary, the distribution of will be related to d. Therefore, after dividing each element in by , the variance returns to 1. This decouples the steepness of the distribution of from d, thus stabilizing the gradient values during training.

Thus, the most core content of Self-Attention has been explained. For more details on the Transformer, you can refer to my previous answer:

Finally, I would like to add that for self-attention, it performs attention with every input vector, so it does not consider the order of the input sequence. To put it simply, you can notice that in our previous calculations, each word vector computes the inner product with other word vectors, resulting in a loss of the original sequence information of the text. In contrast, LSTM interprets the order information of the text by the sequential output of word vectors, while our calculations above completely ignore this aspect of sequence order; if you shuffle the order of the word vectors, the result remains the same.

This leads to the positional encoding of the Transformer, which we will not discuss here.

Implementation Code for Self-Attention

# Implementation of Multi-head Attention mechanism
from math import sqrt
import torch
import torch.nn


class Self_Attention(nn.Module):
    # input : batch_size * seq_len * input_dim
    # q : batch_size * input_dim * dim_k
    # k : batch_size * input_dim * dim_k
    # v : batch_size * input_dim * dim_v
    def __init__(self,input_dim,dim_k,dim_v):
        super(Self_Attention,self).__init__()
        self.q = nn.Linear(input_dim,dim_k)
        self.k = nn.Linear(input_dim,dim_k)
        self.v = nn.Linear(input_dim,dim_v)
        self._norm_fact = 1 / sqrt(dim_k)
        
    
def forward(self,x):
        Q = self.q(x) # Q: batch_size * seq_len * dim_k
        K = self.k(x) # K: batch_size * seq_len * dim_k
        V = self.v(x) # V: batch_size * seq_len * dim_v
         
        atten = nn.Softmax(dim=-1)(torch.bmm(Q,K.permute(0,2,1))) * self._norm_fact # Q * K.T() # batch_size * seq_len * seq_len
        
        output = torch.bmm(atten,V) # Q * K.T() * V # batch_size * seq_len * dim_v
        
        return output

# Implementation of Multi-head Attention mechanism
from math import sqrt
import torch
import torch.nn


class Self_Attention_Muti_Head(nn.Module):
    # input : batch_size * seq_len * input_dim
    # q : batch_size * input_dim * dim_k
    # k : batch_size * input_dim * dim_k
    # v : batch_size * input_dim * dim_v
    def __init__(self,input_dim,dim_k,dim_v,nums_head):
        super(Self_Attention_Muti_Head,self).__init__()
        assert dim_k % nums_head == 0
        assert dim_v % nums_head == 0
        self.q = nn.Linear(input_dim,dim_k)
        self.k = nn.Linear(input_dim,dim_k)
        self.v = nn.Linear(input_dim,dim_v)
        
        self.nums_head = nums_head
        self.dim_k = dim_k
        self.dim_v = dim_v
        self._norm_fact = 1 / sqrt(dim_k)
        
    
def forward(self,x):
        Q = self.q(x).reshape(-1,x.shape[0],x.shape[1],self.dim_k // self.nums_head) 
        K = self.k(x).reshape(-1,x.shape[0],x.shape[1],self.dim_k // self.nums_head) 
        V = self.v(x).reshape(-1,x.shape[0],x.shape[1],self.dim_v // self.nums_head)
        print(x.shape)
        print(Q.size())

        atten = nn.Softmax(dim=-1)(torch.matmul(Q,K.permute(0,1,3,2))) # Q * K.T() # batch_size * seq_len * seq_len
        
        output = torch.matmul(atten,V).reshape(x.shape[0],x.shape[1],-1) # Q * K.T() * V # batch_size * seq_len * dim_v
        
        return output

For more details, please refer to the original paper.

For more exciting content, please follow the Maiwei AI Study Group, every evening at seven o’clock, don’t miss it!

© THE END

For submissions or inquiries, please contact WeChat: MaiweiE_com

GitHub Chinese open-source project “Computer Vision Practical Exercises: Algorithms and Applications”, “free”, “comprehensive”, “cutting-edge”, mainly focused on practice, with detailed documentation, runnable notebooks, and source code.

• Project Address: https://github.com/Charmve/computer-vision-in-action

• Project Homepage: https://charmve.github.io/L0CV-web/