Understanding Q, K, V in Attention Mechanisms

MLNLP(Machine Learning Algorithms and Natural Language Processing) community is one of the largest natural language processing communities in China and abroad, gathering over 500,000 subscribers, covering NLP master’s and doctoral students, university teachers, and corporate researchers.

The Vision of the Community is to promote communication and progress between the academic and industrial communities of natural language processing and machine learning enthusiasts in China and abroad.

Source | Zhihu Q&A

Address | https://www.zhihu.com/question/298810062

This article is for academic sharing only. If there is any infringement, please contact us to delete it.

Answer 1: Author – Not Uncle

Let’s directly implement a Self-Attention using torch:

1. First, define three linear transformation matrices: query, key, value:

class BertSelfAttention(nn.Module):
    self.query = nn.Linear(config.hidden_size, self.all_head_size) # Input 768, Output 768
    self.key = nn.Linear(config.hidden_size, self.all_head_size) # Input 768, Output 768
    self.value = nn.Linear(config.hidden_size, self.all_head_size) # Input 768, Output 768

Note that here, query, key, and value are just names for operations (linear transformations), and the actual Q/K/V are their outputs.

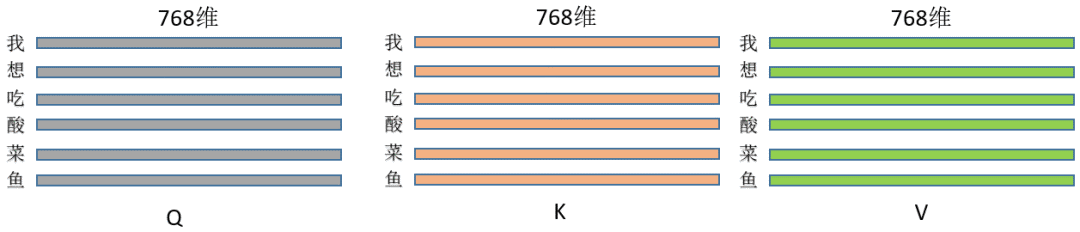
2. Assume the inputs for these three operations are the same matrix (let’s not worry about why the input is the same matrix for now), let’s say it’s a sentence of length L, with each token having a feature dimension of 768, then the input is (L, 768), where each row is a character, like this:

Understanding Q, K, V in Attention Mechanisms

By multiplying the three operations above, we get Q/K/V, (L, 768)*(768,768) = (L,768), the dimensions actually remain unchanged, so the current Q/K/V are:

The code is:

class BertSelfAttention(nn.Module):
    def __init__(self, config):
        self.query = nn.Linear(config.hidden_size, self.all_head_size) # Input 768, Output 768
        self.key = nn.Linear(config.hidden_size, self.all_head_size) # Input 768, Output 768
        self.value = nn.Linear(config.hidden_size, self.all_head_size) # Input 768, Output 768
    
    def forward(self, hidden_states): # hidden_states dimension is (L, 768)
        Q = self.query(hidden_states)
        K = self.key(hidden_states)
        V = self.value(hidden_states)

3. Now to implement this operation:

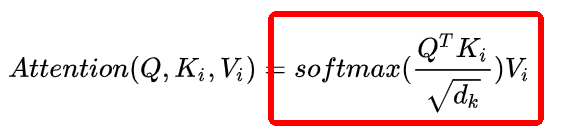
① First, multiply the Q and K matrices, (L, 768)*(L, 768) transposed = (L,L), see the figure:

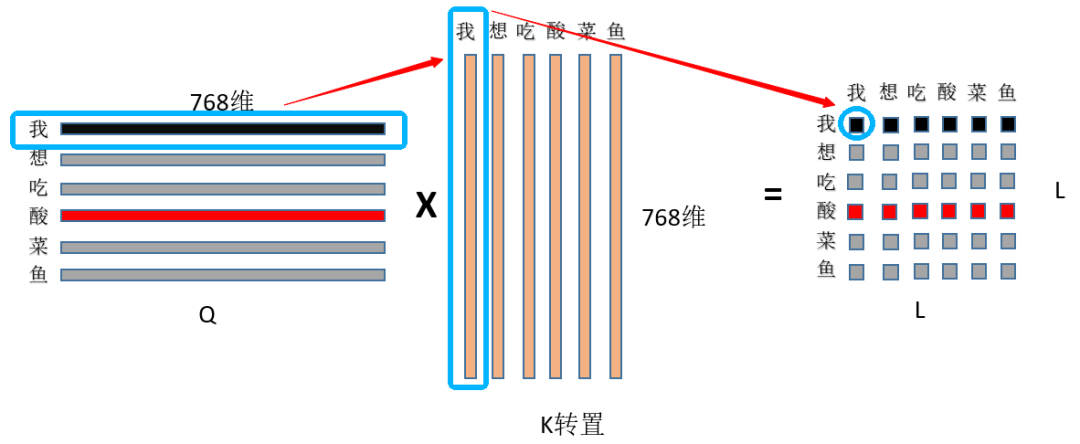
First, use the first row of Q, which is the 768 features of the character “I”, and take the dot product with the 768 features of the character

Leave a Comment Cancel reply