Understanding Neural Networks, Manifolds, and Topology Through 18 Visuals

So far, a major concern about neural networks is that they are difficult to interpret black boxes. This article primarily explains theoretically why neural networks perform so well in pattern recognition and classification. Essentially, they distort and transform the original input through layers of affine transformations and nonlinear transformations until different categories can be easily distinguished.In fact, the backpropagation algorithm (BP) continuously fine-tunes this distortion effect based on training data. This article uses multiple dynamic images to vividly explain how neural networks work.

Author | Christopher Olah

Source | Datawhale

Translation | Liu Yang

Proofreading | Hu Yanjun (OneFlow)

About ten years ago, deep neural networks began to achieve breakthrough results in fields such as computer vision, attracting great interest and attention.

However, some people still express concerns. One reason is that neural networks are black boxes: if a neural network is well-trained, it can achieve high-quality results, but it is difficult to understand how it works. If a neural network fails, it is also challenging to identify the problem.

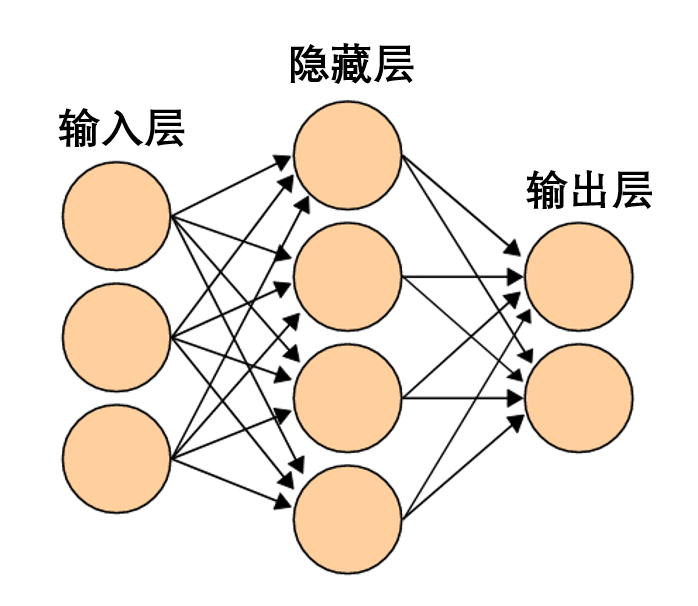
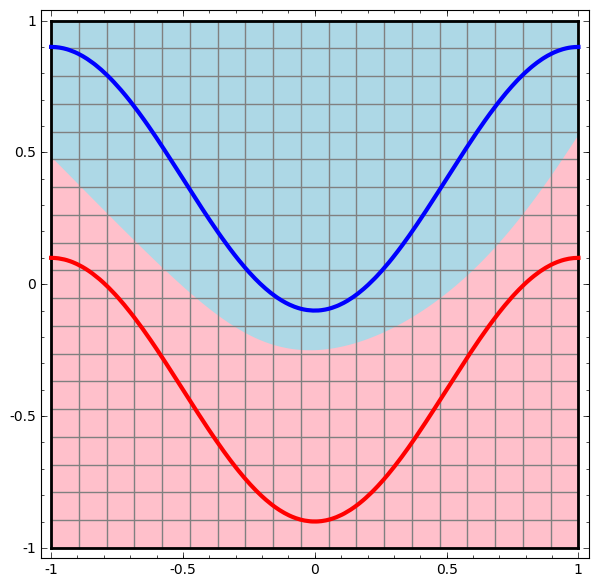
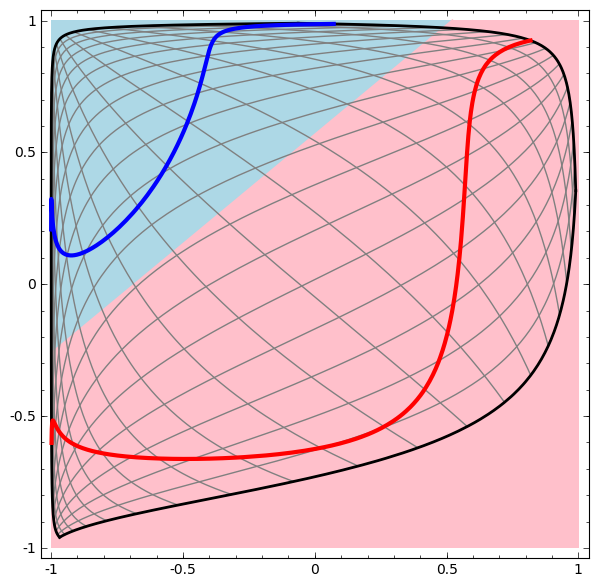
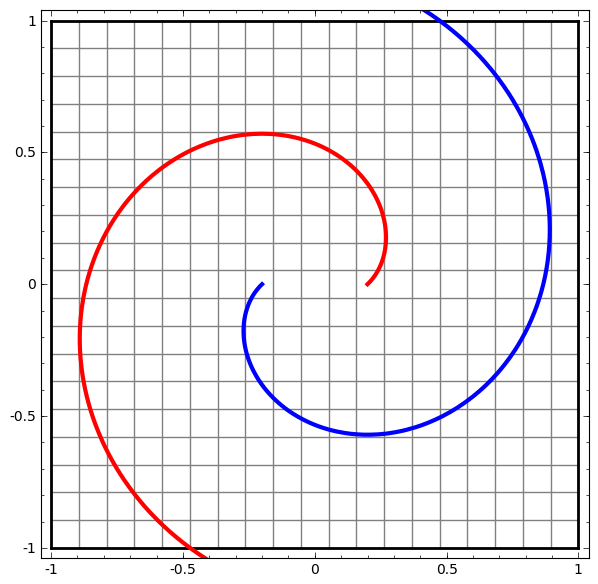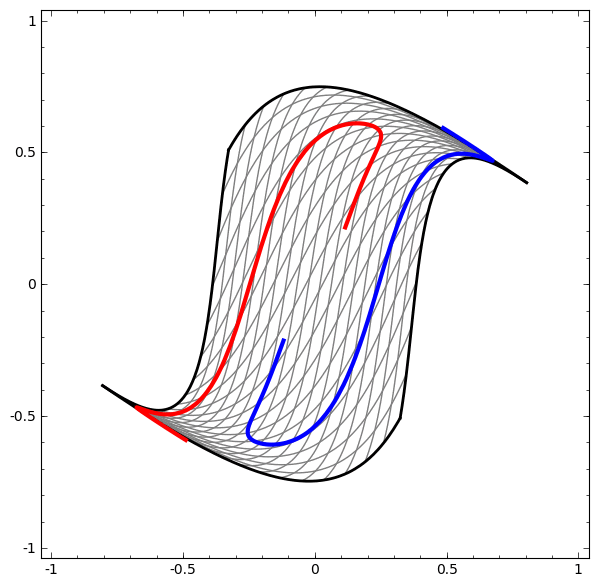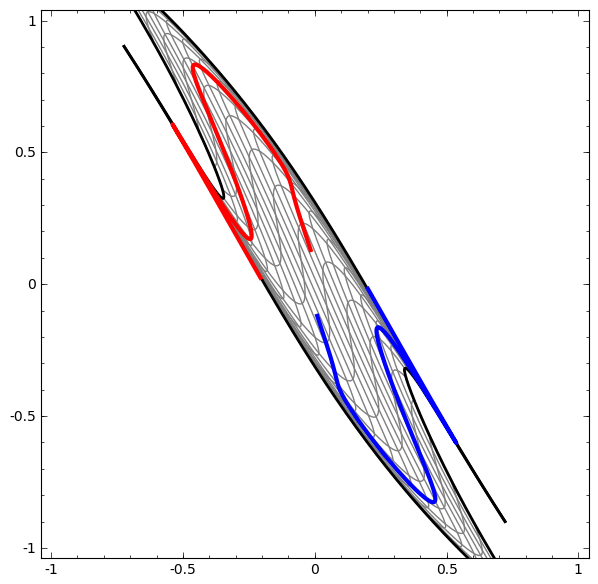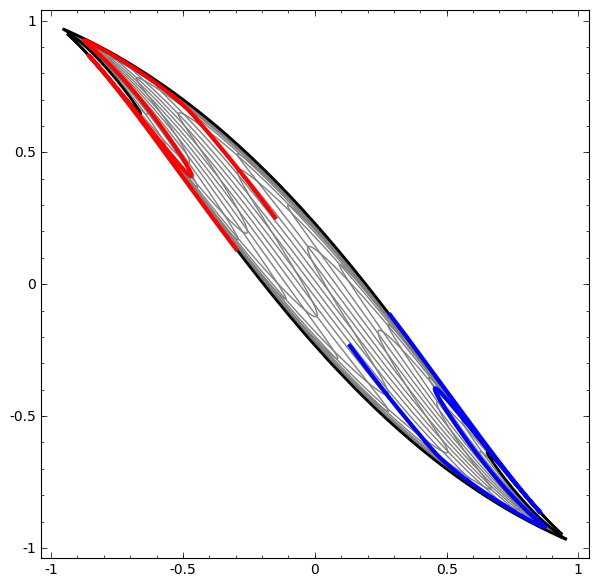
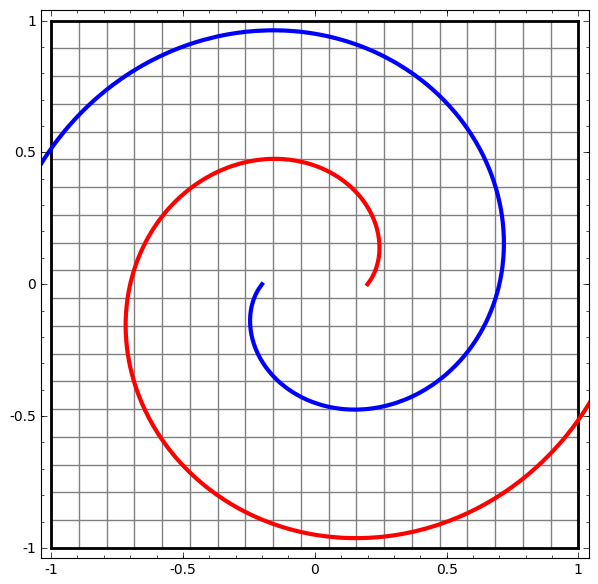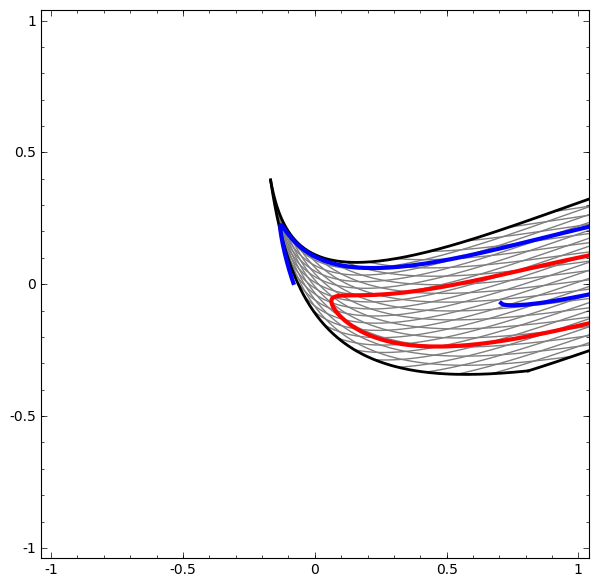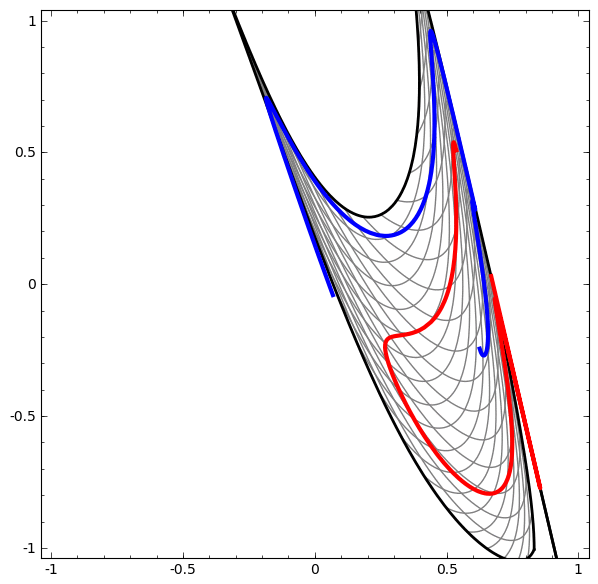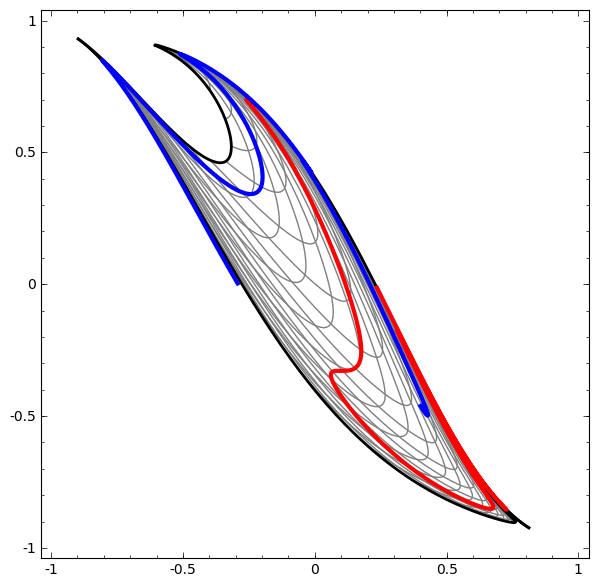
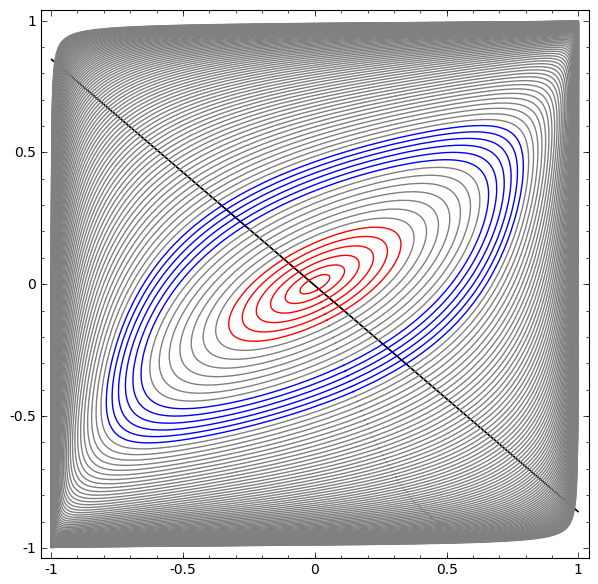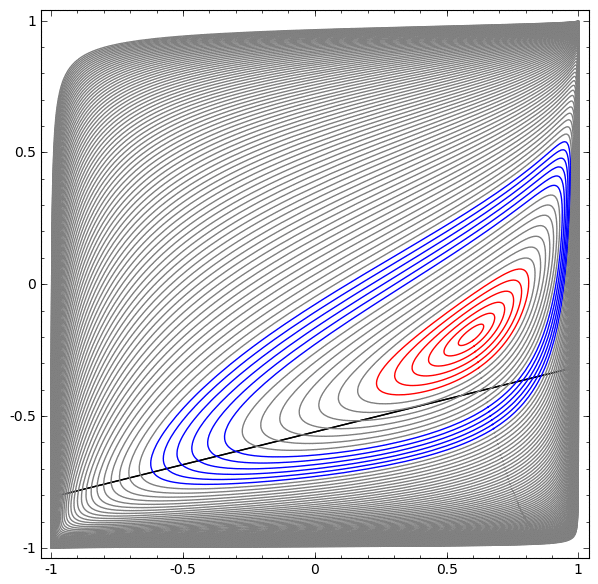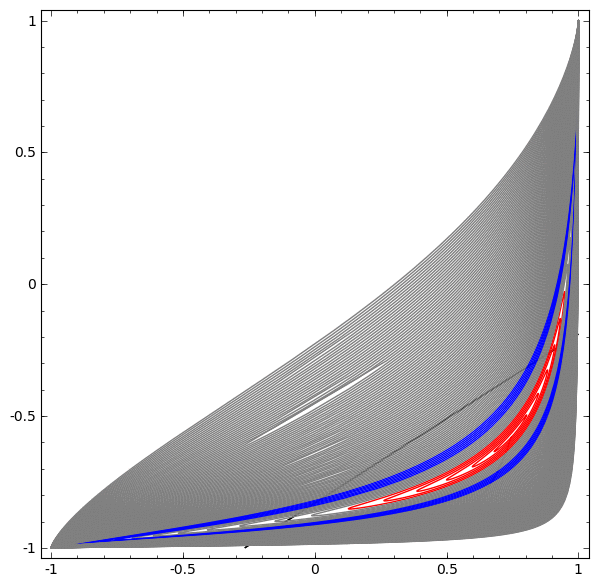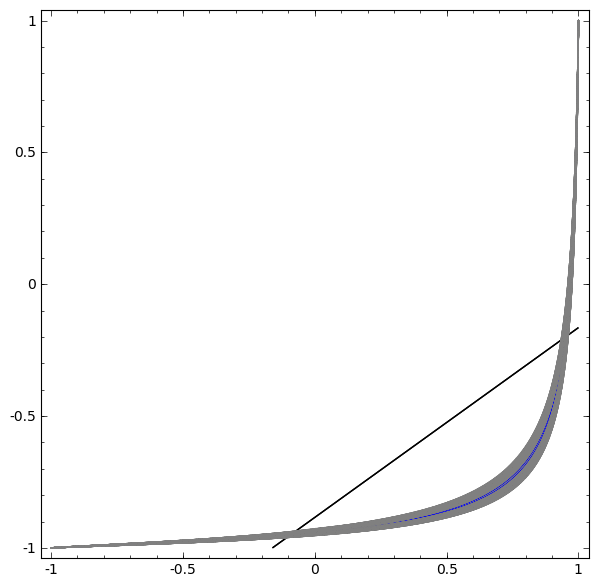
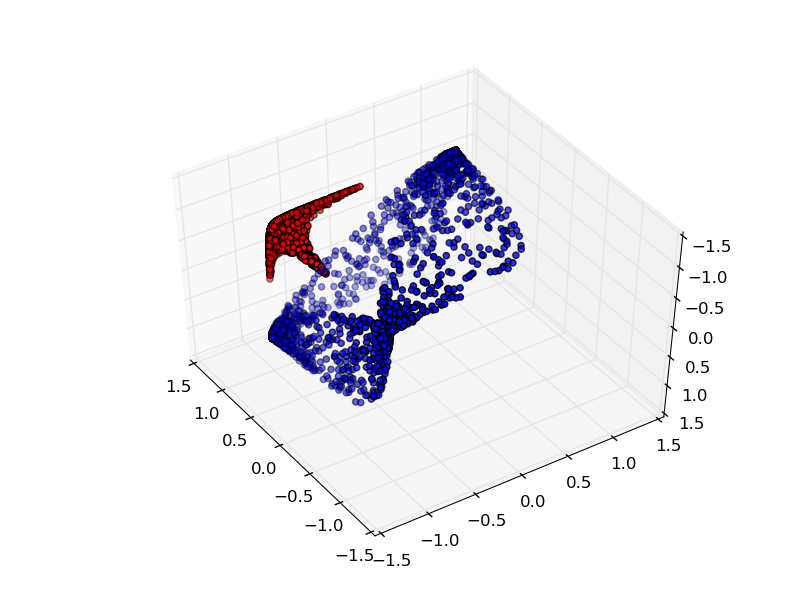
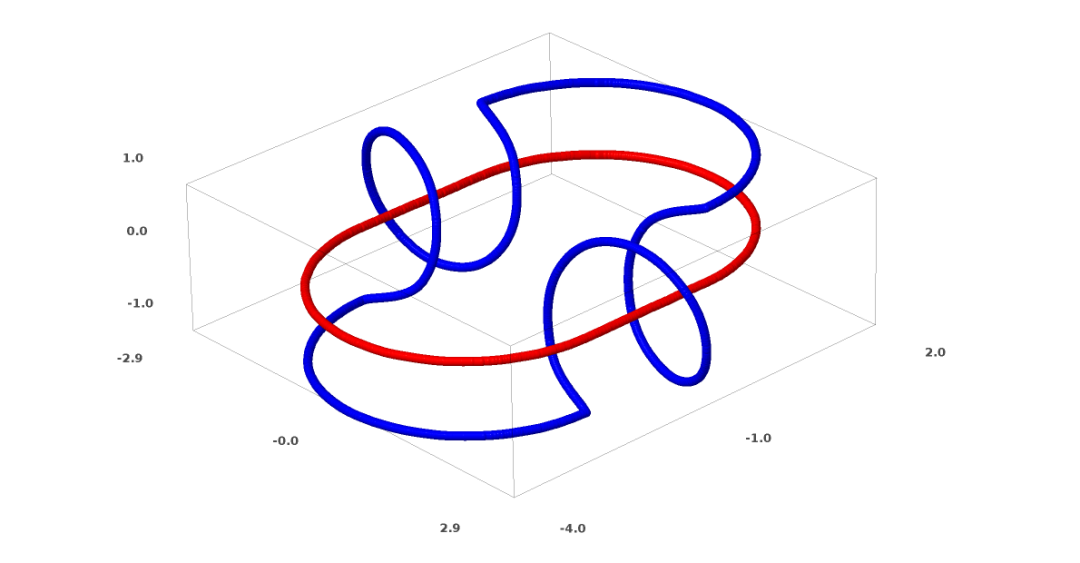
Although it is difficult to understand deep neural networks as a whole, we can start with low-dimensional deep neural networks, which are networks with only a few neurons per layer, making them much easier to understand. We can use visualization methods to understand the behavior and training of low-dimensional deep neural networks. Visualization methods allow us to intuitively understand the behavior of neural networks and observe the connection between neural networks and topology.

Next, I will discuss many interesting things, including the lower bounds of the complexity of neural networks that can classify specific datasets.

A Simple Example

Let’s start with a very simple dataset. In the figure below, two curves on the plane consist of countless points. The neural network will try to distinguish which points belong to which line.

To observe the behavior of the neural network (or any classification algorithm), the most direct method is to see how it classifies each data point.

We start by observing the simplest neural network, which has only one input layer and one output layer. Such a neural network separates the two classes of data points with a straight line.

This neural network is too simple and crude. Modern neural networks usually have multiple layers between the input layer and the output layer, known as hidden layers. Even the simplest modern neural networks have at least one hidden layer.

A simple neural network, image source Wikipedia

Similarly, we observe the operations the neural network performs on each data point. It can be seen that this neural network uses a curve instead of a straight line to separate the data points. Clearly, the curve is more complex than the straight line.

Each layer of the neural network represents data with a new representation. We can observe how the data transforms into new representations and how the neural network classifies them. In the representation of the last layer, the neural network will draw a line to distinguish between the two classes of data (if in a higher dimension, it will draw a hyperplane).

In the previous visualization, we saw the original representation of the data. You can think of it as how the data looks in the “input layer.” Now let’s see how the data looks after transformation, which you can think of as how the data looks in the “hidden layer.”

Each dimension of the data corresponds to the activation of a neuron in the neural network layer.

The hidden layers represent data in such a way that it can be separated by a straight line (i.e., linearly separable).

Continuous Visualization of Layers

In the previous method, each layer of the neural network represents data with different representations. This makes the representations between each layer discrete and not continuous.

This creates difficulties in our understanding. How does the transformation occur from one representation to another? Fortunately, the properties of neural network layers make this understanding very easy.

There are various different layers in neural networks. Below we will discuss the tanh layer as a specific example. A tanh layer includes:

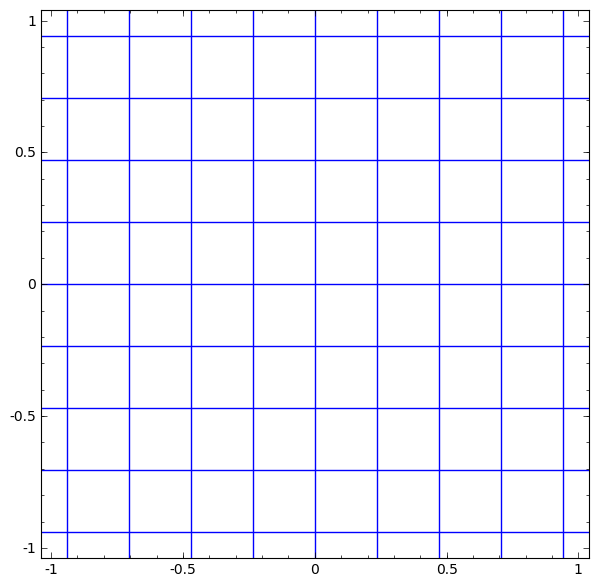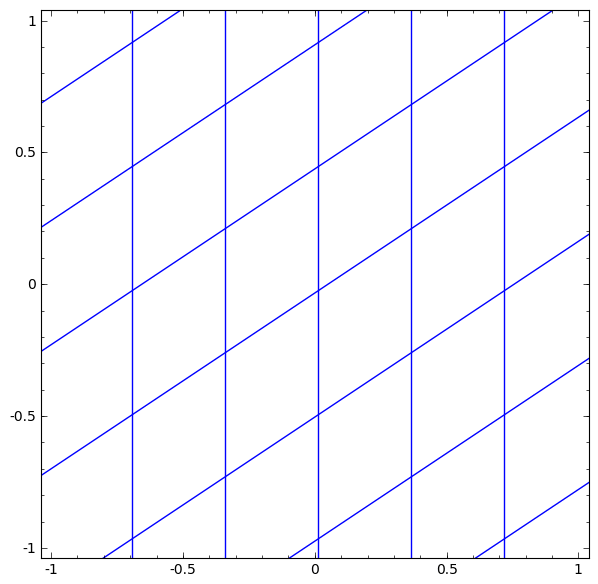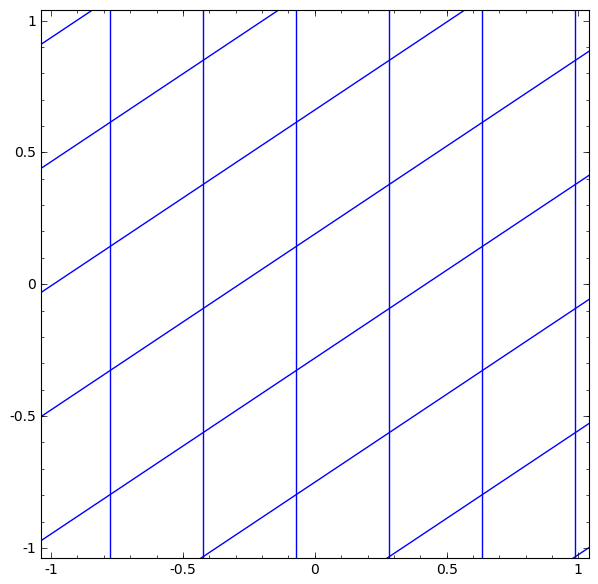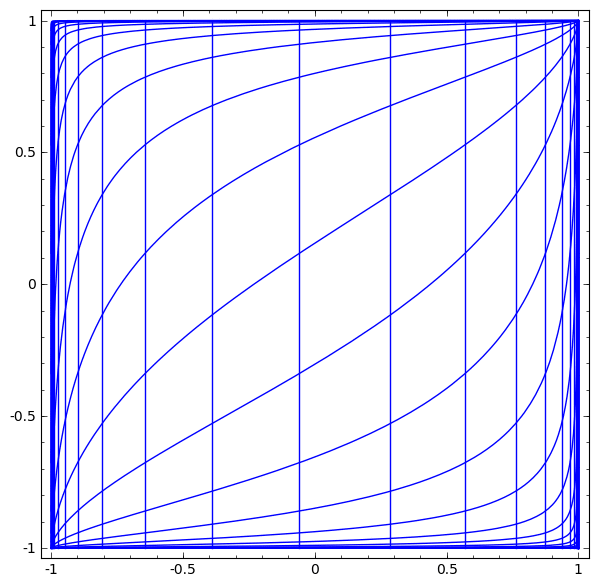
Linear transformation using the “weight” matrix W
Translation using vector b
Pointwise representation using tanh

We can view it as a continuous transformation, as shown below:

Other standard layers are similar, consisting of affine transformations and pointwise applications of monotonic activation functions.

We can use this method to understand more complex neural networks. For example, the neural network below uses four hidden layers to classify two slightly intertwined spiral lines. It can be seen that in order to classify the data, the representation of the data is continuously transformed. The two spiral lines were initially entangled, but in the end, they can be separated by a straight line (linearly separable).

On the other hand, the neural network below, although also using multiple hidden layers, cannot separate two more deeply intertwined spiral lines.

It should be noted that the above two spiral line classification tasks have some challenges because we are currently using only low-dimensional neural networks. If we use a wider neural network, everything would be much easier.

(Andrej Karpathy created a great demo based on ConvnetJS that allows interactive exploration of neural networks through this visualization.)

Topology of the Tanh Layer

Each layer of the neural network stretches and compresses the space, but it does not shear, tear, or fold the space. Intuitively, neural networks do not destroy the topological properties of the data. For example, if a set of data is continuous, then it remains continuous after being transformed into a new representation (and vice versa).

Such transformations that do not affect topological properties are called homeomorphisms. Formally, they are bijections of continuous functions.

Theorem: If the weight matrix W is non-singular (non-singular), and a layer of the neural network has N inputs and N outputs, then the mapping of this layer is a homeomorphism (for specific domains and codomains).

Proof: Let’s go step by step:

1. Assume W has a non-zero determinant. Then it is a bijective linear function with a linear inverse. Linear functions are continuous. Therefore, transformations like “multiplying by W” are homeomorphic;

2. The “translation” transformation is homeomorphic;

3. Tanh (as well as sigmoid and softplus, but not including ReLU) is a continuous function with continuous inverses (for specific domains and codomains) and is bijective, and pointwise applications of them are homeomorphic.

Thus, if W has a non-zero determinant, this layer of the neural network is homeomorphic.

If we combine such layers arbitrarily, this result still holds.

Topology and Classification

Let’s look at a two-dimensional dataset containing two classes of data A and B:

A is red, B is blue

Note: To classify this dataset, the neural network (regardless of depth) must have a layer containing 3 or more hidden units.

As mentioned earlier, using sigmoid units or softmax layers for classification is equivalent to finding a hyperplane (in this case, a straight line) in the representation of the last layer to separate A and B. If there are only two hidden units, the neural network cannot separate the data topologically in this way, and thus cannot classify the above dataset.

In the visualization below, the transformations of the hidden layer change the representation of the data, and the line is the dividing line. It can be seen that the dividing line continually rotates and moves, yet it still fails to effectively separate classes A and B.

This neural network will never be able to perform well in the classification task no matter how much it is trained.

In the end, it can only barely achieve a local minimum with an accuracy of 80% in classification.

The above example has only one hidden layer, and since there are only two hidden units, it will fail to classify regardless.

Proof: If there are only two hidden units, either the transformation of this layer is homeomorphic, or the weight matrix of the layer has a determinant of 0. If it is homeomorphic, A is still surrounded by B, and cannot be separated by a straight line. If the determinant is 0, then the dataset will fold along some axis. Since A is surrounded by B, any folding of A along any axis will cause some A data points to mix with B, making it impossible to distinguish A from B.

But if we add a third hidden unit, the problem will be easily solved. At this point, the neural network can transform the data into the following representation:

At this point, it can be separated by a hyperplane.

To better explain its principle, here is a simpler one-dimensional dataset example:

To classify this dataset, a layer consisting of two or more hidden units must be used. If two hidden units are used, a nice curve can represent the data, allowing it to be separated by a straight line:

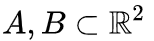
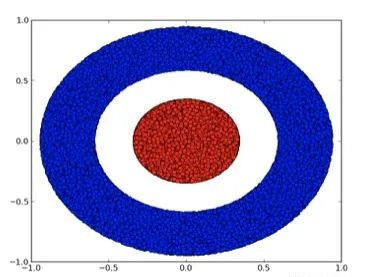
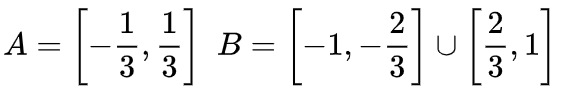
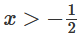How is this achieved? When Understanding Neural Networks, Manifolds, and Topology Through 18 Visuals

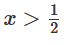is activated, one hidden unit is activated; when Understanding Neural Networks, Manifolds, and Topology Through 18 Visuals

is activated, the other hidden unit is activated. When the first hidden unit is activated while the second hidden unit is not, it can be determined that this is a data point belonging to class A.

Manifold Hypothesis

Does the manifold hypothesis make sense for handling real-world datasets (such as image data)? I believe it does.

The manifold hypothesis states that natural data forms low-dimensional manifolds in its embedded space. This hypothesis is supported by both theoretical and experimental evidence. If you believe in the manifold hypothesis, then the task of classification algorithms can be reduced to separating a set of entangled manifolds.

In the previous example, one class completely surrounds another class. However, in real-world data, the manifold of dog images is unlikely to be completely surrounded by the manifold of cat images. Nevertheless, other more reasonable topological situations may still pose problems, which will be discussed in the next section.

Links and Homotopy

Next, I will talk about another interesting dataset: two linked tori, A and B.

Similar to the previous dataset situations, if we do not use n+1 dimensions, we cannot separate an n-dimensional dataset (where n+1 dimension in this case is the 4th dimension).

The linking problem belongs to knot theory in topology. Sometimes, we see a link, and we cannot immediately determine whether it is an unlink (unlink means that although they are entangled, they can be separated through continuous deformation).

A simpler unlink

If a neural network with only 3 hidden units can classify a dataset, then this dataset is an unlink (the question arises: theoretically, can all unlinks be classified by a neural network with only 3 hidden units?).

From the perspective of knot theory, the continuous visualization of the data representation generated by the neural network is not only a great animation but also a process of untangling the link. In topology, we refer to this as the ambient isotopy between the original link and the separated link.

The ambient isotopy between manifolds A and B is a continuous function:

Each

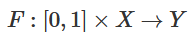
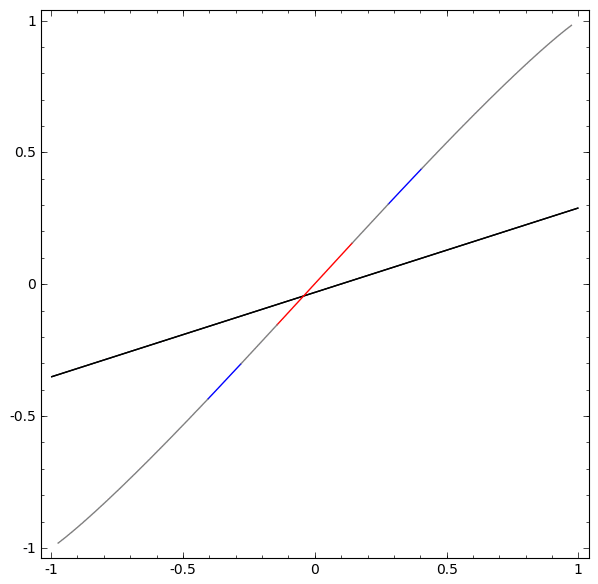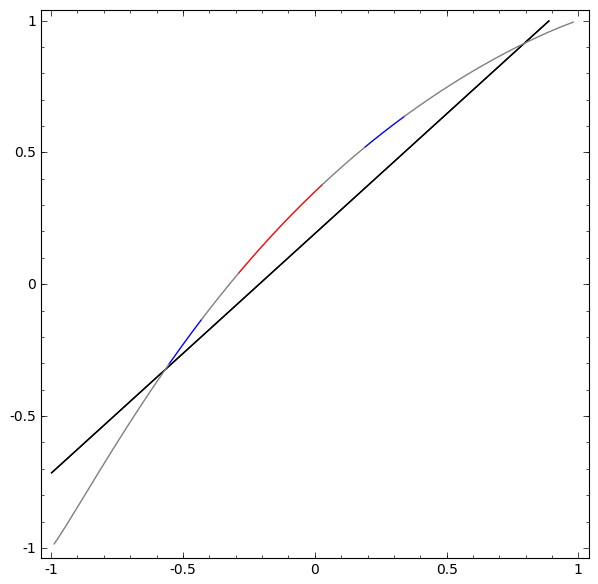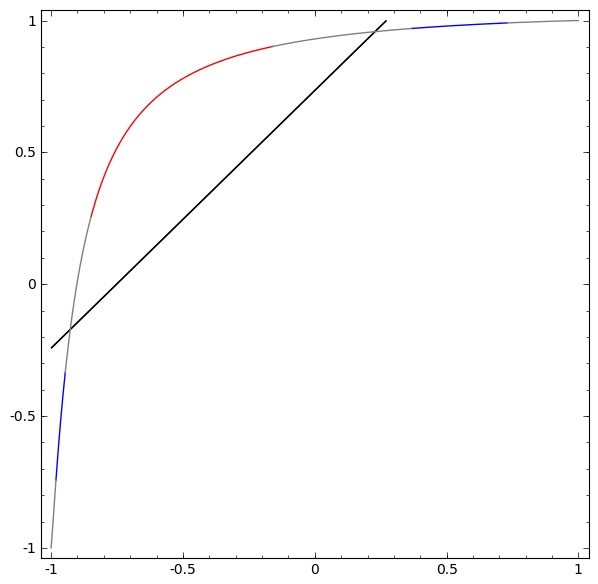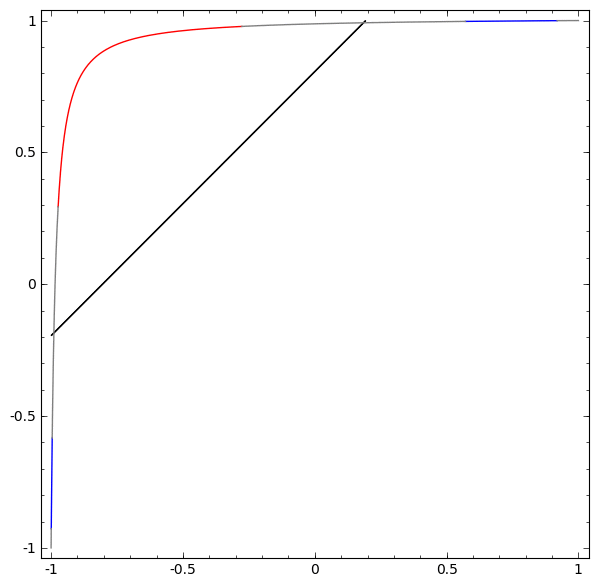
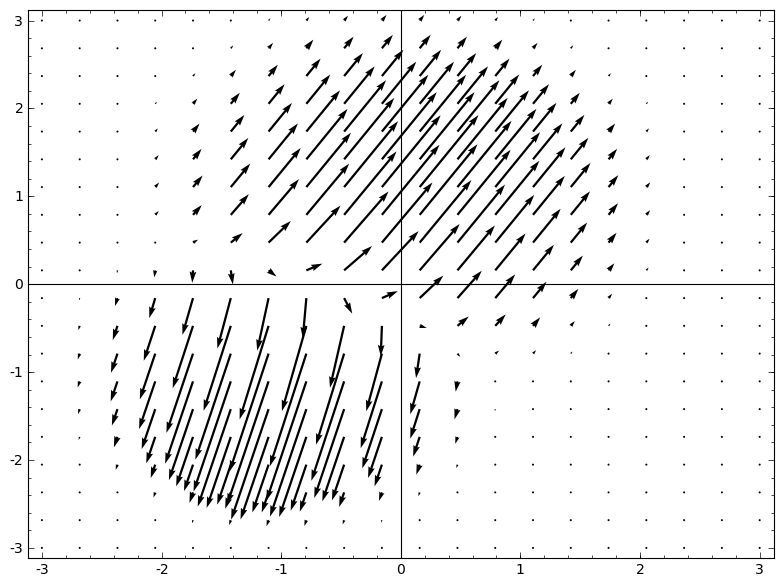
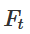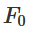is homeomorphic to X. Understanding Neural Networks, Manifolds, and Topology Through 18 Visuals

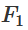is the characteristic function, Understanding Neural Networks, Manifolds, and Topology Through 18 Visuals

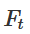maps A to B. That is, Understanding Neural Networks, Manifolds, and Topology Through 18 Visuals

continuously transitions from mapping A to itself to mapping A to B.

Theorem: If the following three conditions are met: (1) W is non-singular; (2) the order of neurons in the hidden layer can be manually arranged; (3) the number of hidden units is greater than 1, then there is an ambient isotopy between the input of the neural network and the representations generated by the neural network layers.

Proof: Let’s go step by step:

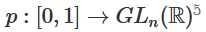1. The most difficult part is the linear transformation. To achieve linear transformation, we need W to have a positive determinant. Our premise is that the determinant is non-zero; if the determinant is negative, we can convert it to positive by swapping two hidden neurons. The space of matrices with positive determinants is path-connected, so there exists Understanding Neural Networks, Manifolds, and Topology Through 18 Visuals

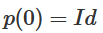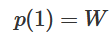therefore, Understanding Neural Networks, Manifolds, and Topology Through 18 Visuals

By the function Understanding Neural Networks, Manifolds, and Topology Through 18 Visuals

we can continuously transition the characteristic function to W transformation, multiplying the matrix 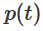Understanding Neural Networks, Manifolds, and Topology Through 18 Visuals

at each point in time.

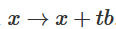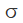2. The transition from the characteristic function to the b translation can be achieved through the function Understanding Neural Networks, Manifolds, and Topology Through 18 Visuals

3. The transition from the characteristic function to Understanding Neural Networks, Manifolds, and Topology Through 18 Visuals

can be achieved through pointwise applications.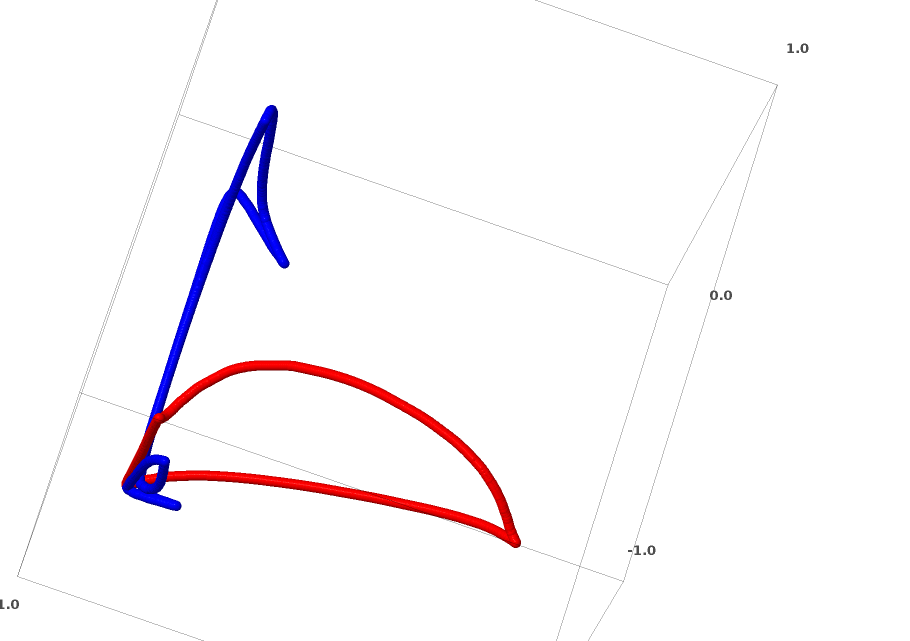

I guess some people might be interested in the following question: Is it possible to develop a program that can automatically discover such ambient isotopy and also automatically prove the equivalence of certain different links or the separability of certain links? I am also curious whether neural networks can outperform the current SOTA techniques in this regard.

Although the forms of links we are discussing now are unlikely to appear in real-world data, real data may have higher-dimensional generalizations.

Links and knots are both 1-dimensional manifolds but require 4 dimensions to separate them. Similarly, to separate n-dimensional manifolds, higher-dimensional space is needed. All n-dimensional manifolds can be separated with 2n+2 dimensions.

A Simple Method

The simplest method for neural networks is to directly pull apart the entangled manifolds, and the more tightly entangled parts are pulled apart, the better. Although this is not the fundamental solution we pursue, it can achieve relatively high classification accuracy, reaching a relatively ideal local minimum.

This method will cause very high derivatives in the areas being stretched. To cope with this, a contraction penalty is needed, which penalizes the derivatives of the layers of data points.

Local minima are of no use in solving topological problems, but topological problems may provide good ideas for exploring solutions to the above issues.

On the other hand, if we only care about achieving good classification results, then if a small part of a manifold is entangled with another manifold, does that pose a problem for us? If we only care about classification results, it seems that this is not a problem.

(My intuition suggests that such shortcut methods are not good and can easily lead to dead ends. Especially in optimization problems, seeking local minima does not truly solve the problem, and if a solution that does not genuinely address the problem is chosen, good performance will ultimately not be achieved.)

Selecting More Suitable Neural Network Layers for Manipulating Manifolds?

I believe standard neural network layers are not suitable for manipulating manifolds because they use affine transformations and pointwise activation functions.

Perhaps we can use a completely different neural network layer?

One idea that comes to mind is to first let the neural network learn a vector field, where the direction of the vector field is the direction we want to move the manifold:

Then deform the space based on this:

We can learn the vector field at fixed points (simply select some fixed points from the training set as anchors) and interpolate in some way. The form of the vector field above is as follows:

Where and are vectors, and are n-dimensional Gaussian functions. This idea is inspired by radial basis functions.

K-Nearest Neighbor Layer

Another perspective I have is that linear separability may be too high and unreasonable a requirement for neural networks, and perhaps using k-nearest neighbors (k-NN) would be better. However, the k-NN algorithm largely relies on the representation of the data, so a good data representation is needed for k-NN to achieve good results.

In the first experiment, I trained some MNIST neural networks (two-layer CNN, no dropout), achieving an error rate of less than 1%. Then, I discarded the final softmax layer and used the k-NN algorithm, with multiple results showing that the error rate decreased by 0.1-0.2%.

However, I feel that this approach is still incorrect. The neural network is still trying to perform linear classification, but because it uses the k-NN algorithm, it can slightly correct some of its mistakes, thus reducing the error rate.

Due to the weighting of (1/distance), k-NN is differentiable with respect to the representation of the data it acts on. Therefore, we can directly train the neural network for k-NN classification. This can be seen as a “nearest neighbor” layer, which functions similarly to the softmax layer.

We do not want to feedback the entire training set for every mini-batch because that would be too costly. I think a good method is to classify each element in the mini-batch based on the categories of the other elements in the mini-batch, assigning each element a weight of (1/(distance to the classification target)).

Unfortunately, even using complex architectures, employing the k-NN algorithm can only reduce the error rate to 4-5%, while simpler architectures have even higher error rates. However, I did not spend much effort on hyperparameters.

But I still like the k-NN algorithm because it is better suited for neural networks. We want points on the same manifold to be closer to each other, rather than being obsessed with separating the manifolds with hyperplanes. This simplifies the problem by shrinking individual manifolds while expanding the space between different categories of manifolds.

Summary

Some topological properties of data may prevent these data from being linearly separable using low-dimensional neural networks (regardless of the depth of the neural network). Even in technically feasible cases, such as spirals, it is very difficult to achieve separation with low-dimensional neural networks.

To accurately classify data, neural networks sometimes require wider layers. Additionally, traditional neural network layers are not suitable for manipulating manifolds; even with manually set weights, it is challenging to obtain ideal data transformation representations. New neural network layers may serve as good auxiliary tools, especially those derived from understanding machine learning from the perspective of manifolds.

(Original translation: https://mp.weixin.qq.com/s/Ph2DADMGzi-HC4lIuU5Byw；

Original text:http://colah.github.io/posts/2014-03-NN-Manifolds-Topology/）

   ABOUT 
    关于我们 


深蓝学院是专注于人工智能的在线教育平台，已有数万名伙伴在深蓝学院平台学习，很多都来自于国内外知名院校，比如清华、北大等。


阅读至此了，分享、点赞、在看三选一吧🙏

Leave a Comment Cancel reply