Introduction: Here comes the valuable content! Udacity Machine Learning course mentor Walker is here to teach you how to understand neural networks in a simple, vivid, and interesting way!
What is a neural network? A neural network is a series of simple nodes that, when combined simply, express a complex function. Let’s explain each one below.

Linear Node
A node is a simple function model with inputs and outputs.
1. The simplest linear node: x + y
The simplest linear node I can think of is x + y.
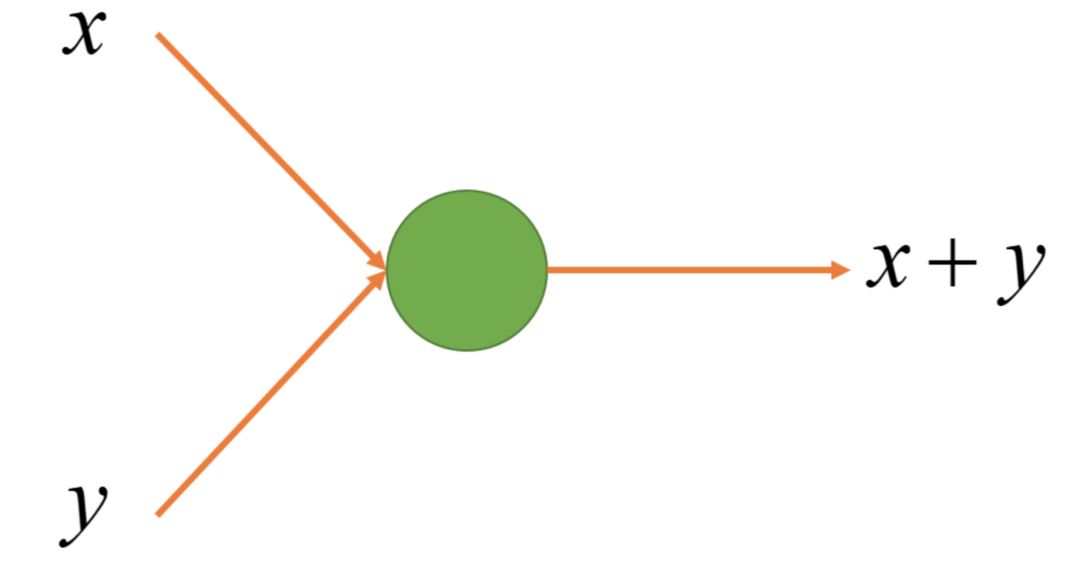
2. Parameterized Linear Node: ax + by
x + y is a special linear combination, we can generalize all linear combinations of x, y, that is, ax + by. The a, b are the parameters of this node. Different parameters can allow the node to represent different functions, but the structure of the node remains the same.
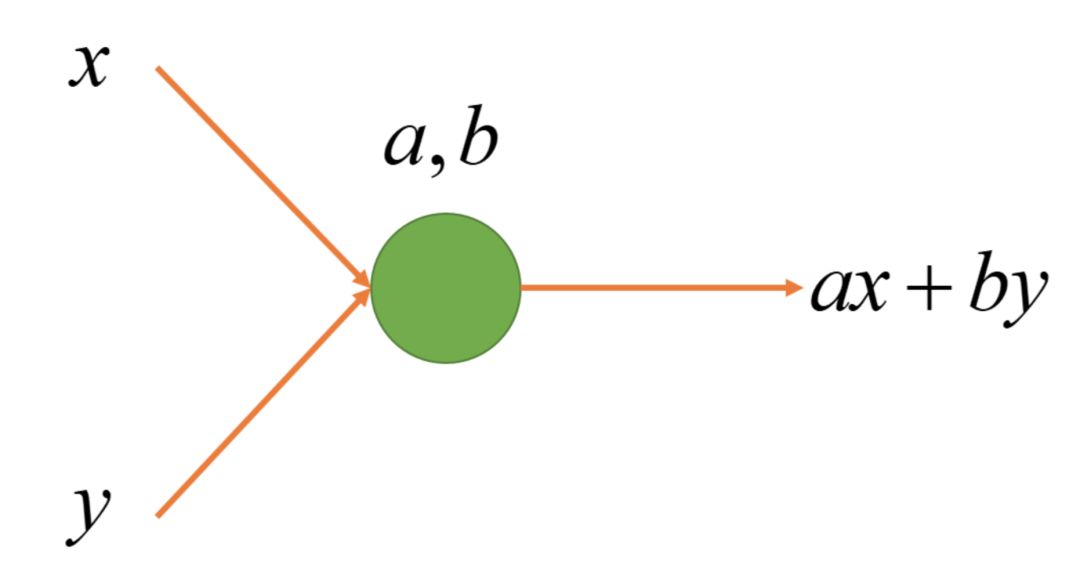
3. Multiple Input Linear Node: a1x1 + a2x2 + a3x3 + … + anxn
We further generalize 2 inputs into any number of inputs. Here a1, a2, a3, … , an are the parameters of this node. Similarly, different parameters can allow the node to represent different functions, but the structure of the node is the same. Note that n is not a parameter of this node; nodes with different input counts have different structures.
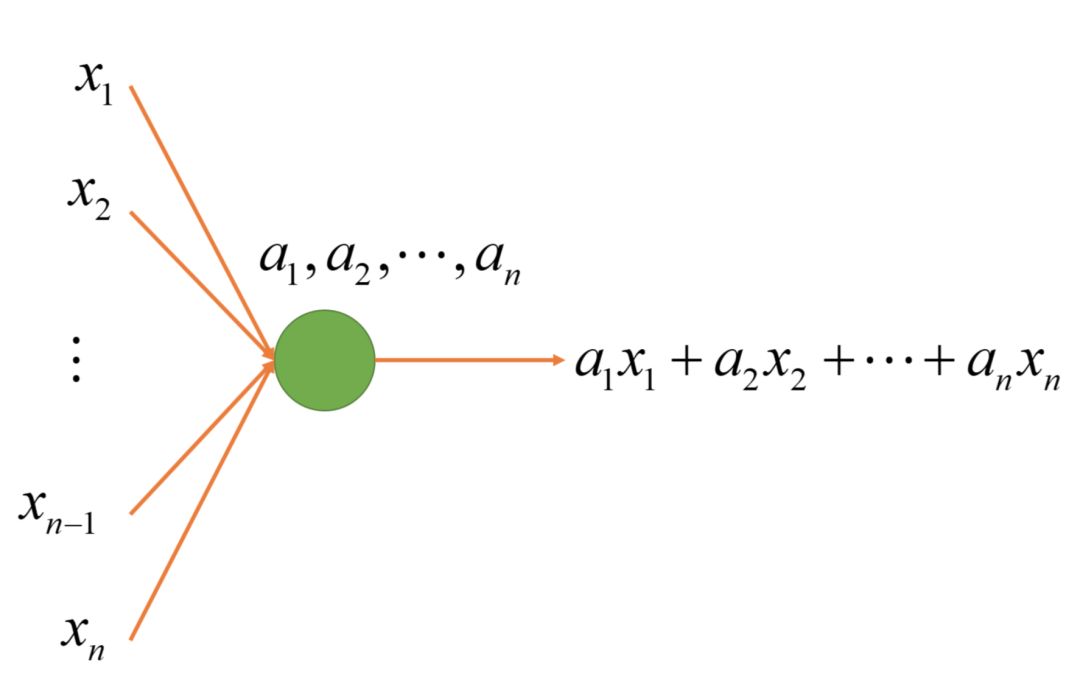
4. Vector Representation of Linear Node: aTx
The above expression is too lengthy, we use the vector x to represent the input vector (x1, x2, . . . , xn), and use the vector a to represent the parameter vector (a1, a2, …, an). It is not difficult to prove that aTx=a1x1 + a2x2 + a3x3 + … + anxn.The vector a is the parameter of this node, and the dimension of this parameter is the same as the dimension of the input vector.
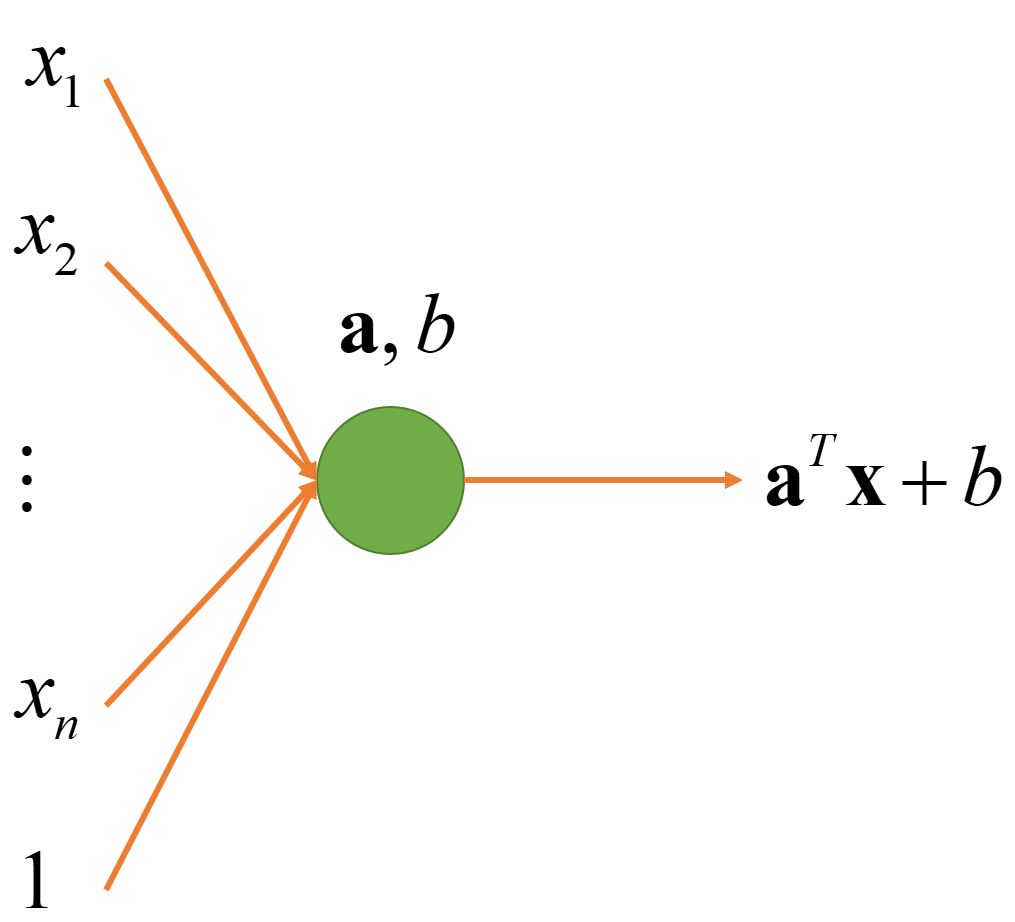
5. Linear Node with Constant: aTx + b
Sometimes, we want the linear node to have an output even when all inputs are 0. Therefore, we introduce a new parameter b as a bias term to increase the expressiveness of the model. Sometimes, for simplicity, we write the expression as aT x. At this time, x = (x1,x2,…,xn,1), a = (a1,a2,…,an,b)
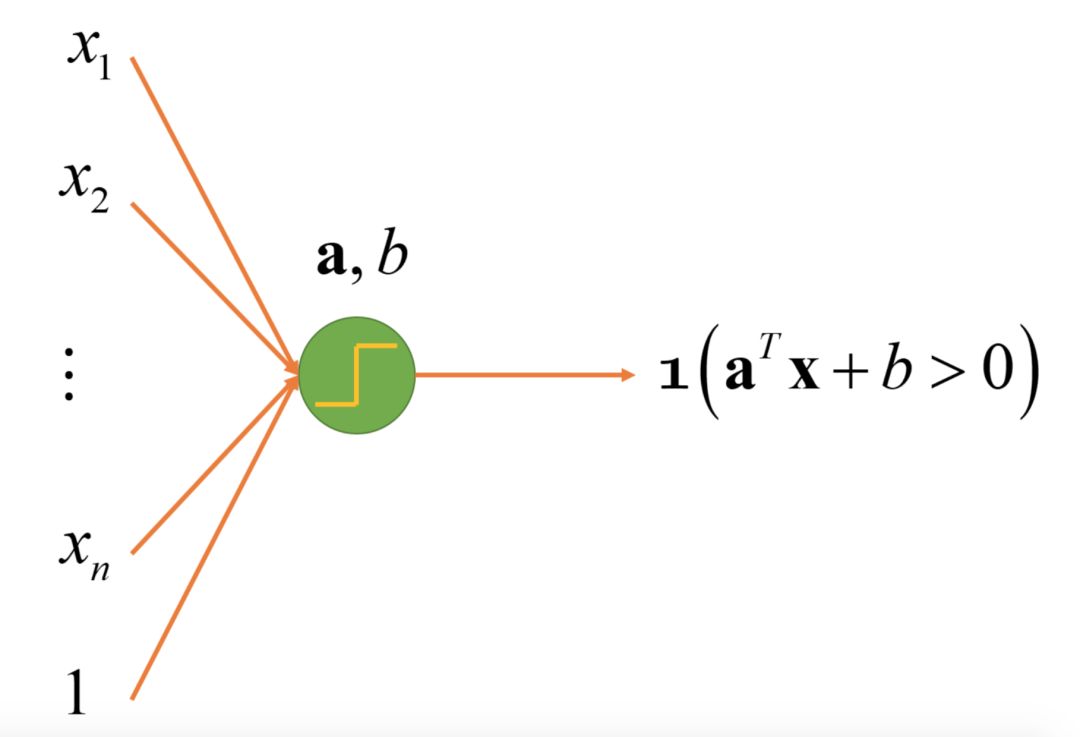
6. Linear Node with Activation Function: 1(aT x + b > 0)
For binary classification problems, the output of the function is either true or false, that is 0 or 1. The function 1 : R → {1, 0} maps true propositions to 1 and false propositions to 0.
Examples of Linear Nodes
1. The linear node expression x ∨ y (or function) has the truth table as follows:
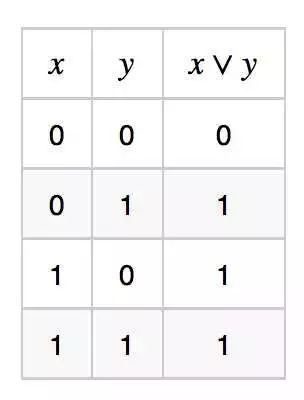
Define the node 1(x + y − 0.5 > 0), it is not difficult to verify that it is equivalent to x ∨ y.

2. The linear node expression x ∧ y (and function) has the truth table as follows:
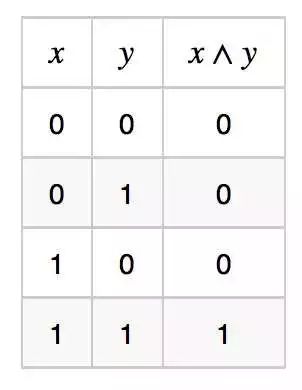
Define the node 1(x + y − 1.5 > 0), it is not difficult to verify that it is equivalent to x ∧ y.
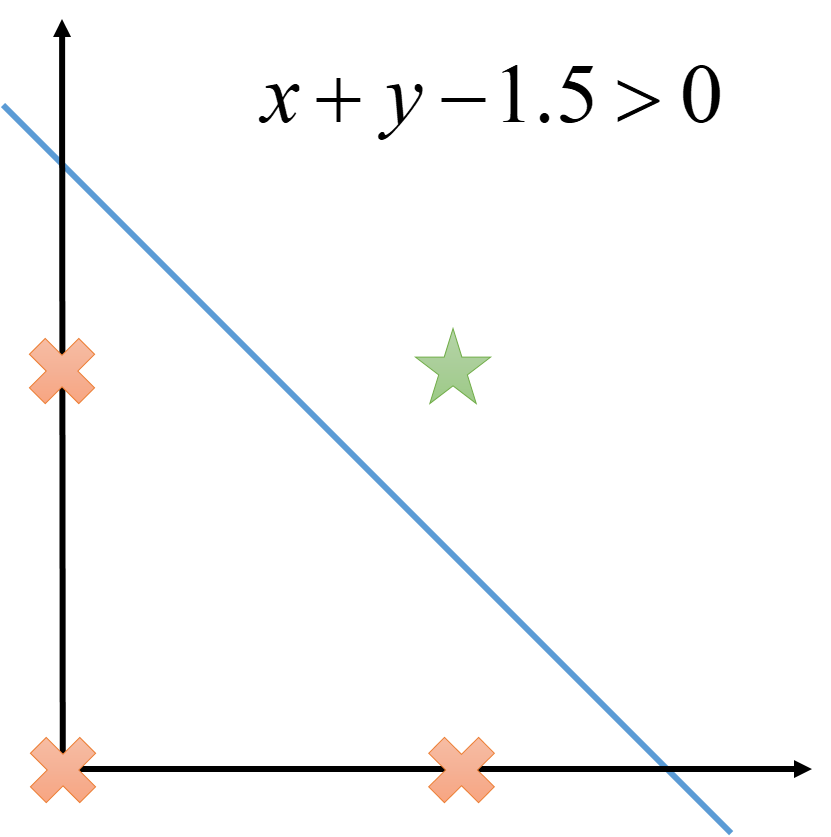
The Expressiveness of Linear Nodes
A single linear node can express all linear functions (function value range is the real number set) and all linearly separable classifications (function value range is {0, 1}). We will not elaborate on the definitions and proofs of concepts here. Although a single linear node is already powerful, it still has limitations. For functions that are linearly inseparable, it is powerless, such as the XOR function x ⊕ y

Combination of Linear Nodes
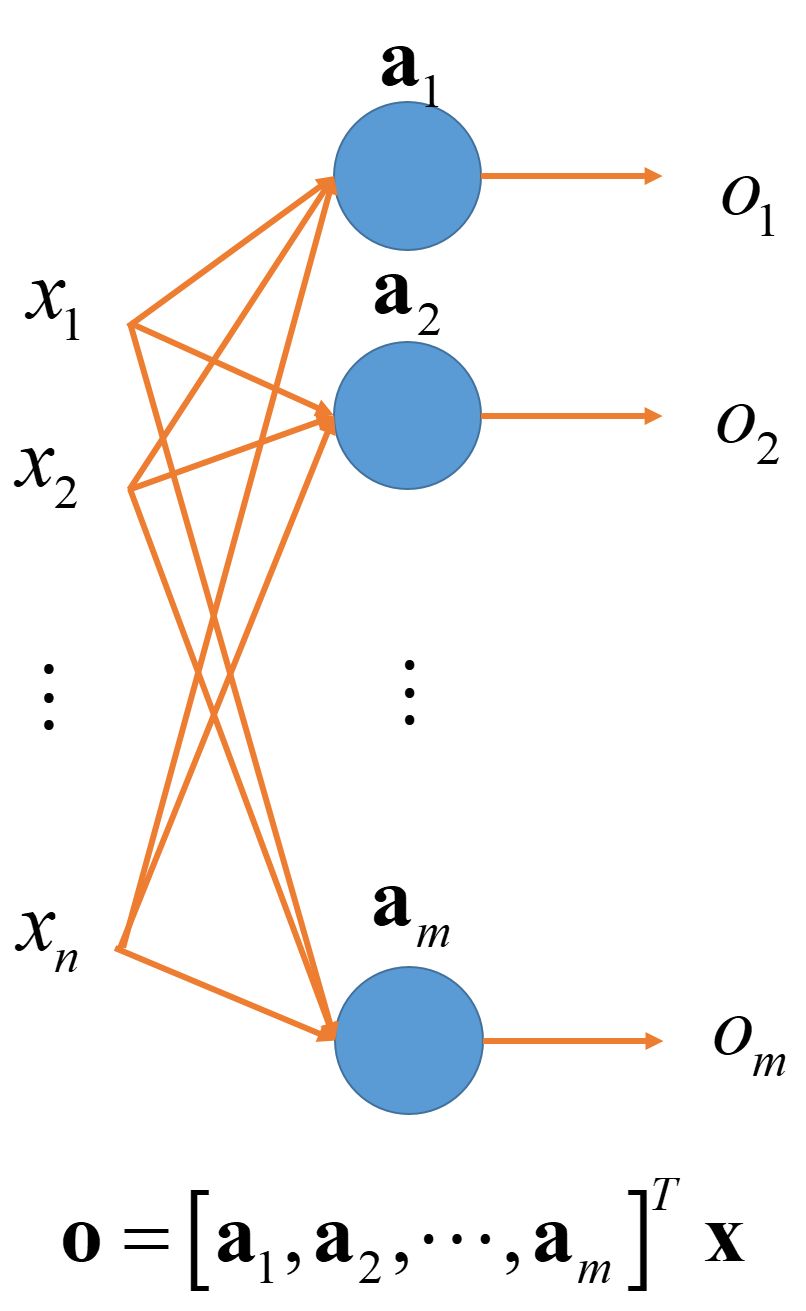
1. Multiple Linear Nodes Combined at the Same Level:WTx
The input of the above linear nodes is multi-dimensional, but the output is only one-dimensional, that is, a real number. If we want multi-dimensional outputs, we can place multiple nodes in parallel. Let a1 ,a2 ,…,am be the parameters of the m nodes, then the outputs will be a1Tx,a2Tx,…,amT x. The final output result is
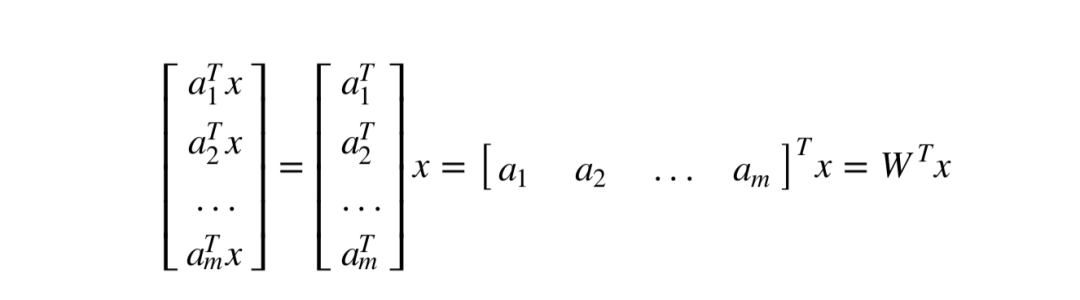
Where W = [a1,a2,…,am] is an n by m parameter matrix.
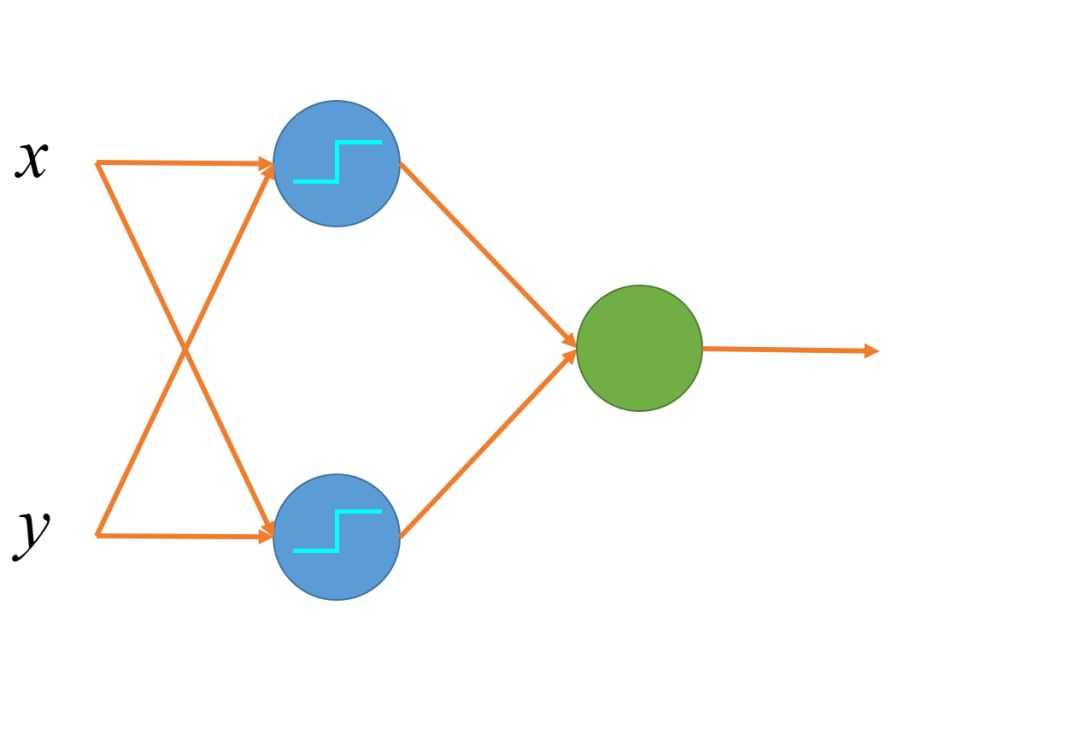
2. Multi-layer Linear Nodes:
In multi-layer linear nodes, a linear node with an activation function in one layer outputs as the input to the next layer. Usually, the intermediate layer (or hidden layer, the blue nodes in the diagram) will have an activation function to increase the expressiveness of the model.(Think: If the hidden layer has no activation function, why are two layers of linear nodes equivalent to one layer?)
Examples of Multi-layer Linear Nodes
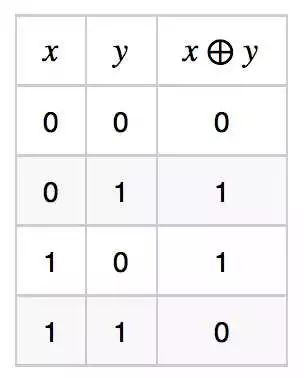
1. Multi-layer expression of the XOR function x ⊕ y, the truth table of the XOR function is:
This is a function that cannot be linearly separated and cannot be expressed by a single linear node. However, we can use multiple layers of linear nodes to accomplish this task.
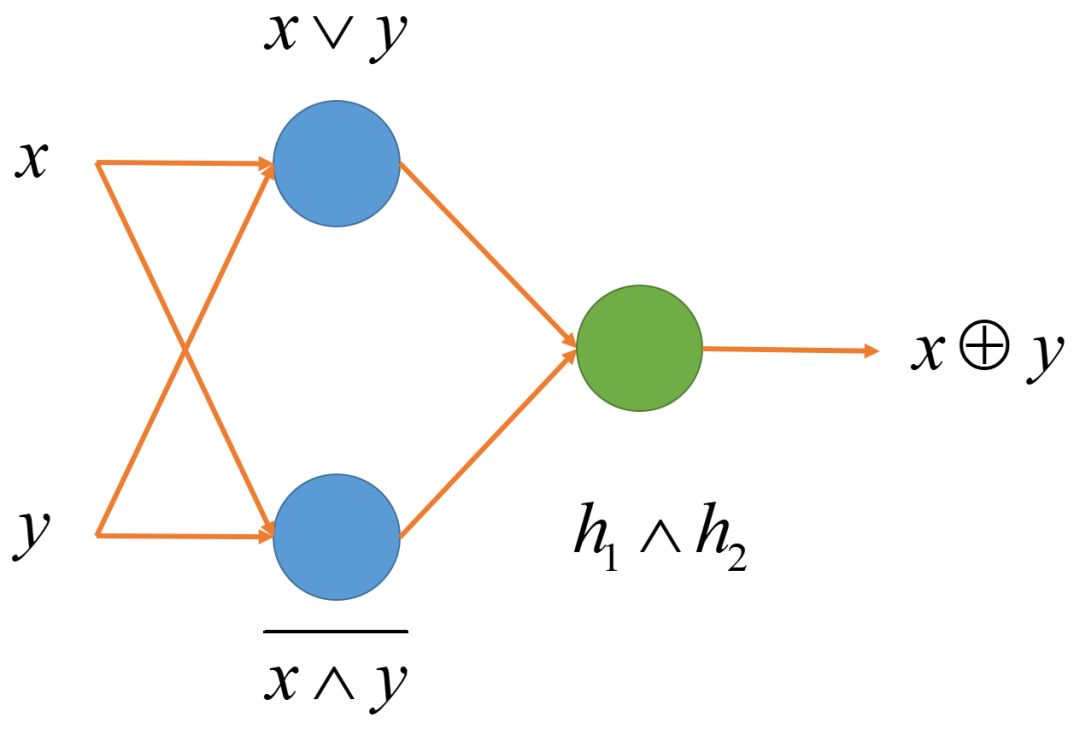
The Expressiveness of Multi-layer Linear Nodes
It can be proven that multi-layer neurons can express all continuous functions. The proof is quite complex; interested fans can check out: A visual proof that neural nets can compute any function

Conclusion
In fact, in this article, we haven’t covered many common nodes, such as ReLu, sigmoid, dropout, etc. Neural networks not only have forward computation but also backpropagation, and the emergence of these nodes is closely related to backpropagation…
If you want to learn artificial intelligence knowledge and skills in a more systematic way and explore new opportunities in the workplace, let the cutting-edge technology education platform Udacity from Silicon Valley help you.

Udacity collaborates with top experts such as the father of autonomous vehicles Sebastian Thrun, the father of GANs Ian Goodfellow, and Google DeepMind scientist Andrew Trask to launch the “Deep Learning Foundation Nanodegree Program”!
During the learning process, you will not only receive guidance from top instructors in Silicon Valley but also challenge super cool practical projects, and enjoy learning services such as one-on-one mentoring, code review, and synchronous study groups from Udacity. Invest 10 hours a week, and even with no background, you can become a Silicon Valley certified deep learning expert!
Upon graduation, you will also enjoy Udacity’s employment recommendation services, gaining more opportunities to join leading technology companies like IBM, Tencent, Didi Chuxing, and more!

Udacity’s top partner companies
How to join such a cool course?
This course is limited to 350 seats; scan the QR code below immediately to seize the opportunity and enjoy the following benefits:
* Silicon Valley-style simulated classroom experience free entry;
* Exclusive “Ultimate Career Guide to Deep Learning”
* Communicate and solve problems with senior students in the field of artificial intelligence

Silicon Valley-style classroom simulated experience
Click [Read the original text] to give yourself a chance to become a Silicon Valley certified deep learning engineer!
