Author: Matthew Stewart
Translator: Che Qianzi
Proofreader: Chen Dan
This article is approximately 5500 words, and it is recommended to read it in 12 minutes.
The knowledge in this article will provide a strong foundation to introduce you to the performance of neural networks, applied in deep learning applications.
“Your brain does not generate thoughts. Your thoughts shape the neural network.” — Deepak Chopra

Quote
J. Nocedal and S. Wright, “Numerical Optimization”, Springer, 1999
TLDR: J. Bullinaria, “Learning with Momentum, Conjugate Gradient Learning”, 2015
This is the first article in a series that elucidates the theory behind neural networks and how to design and implement them. This article aims to provide a detailed and in-depth introduction to neural networks for a wider audience, benefiting readers who know almost nothing about neural networks or those who are somewhat familiar but may not have fully mastered the subject. I will introduce the motivation and fundamentals of neural networks in this article. Future articles will delve deeper into the design and optimization of neural networks and deep learning.
This series of tutorials is largely based on courses from the Computer Science and Data Science departments at Harvard and Stanford.
All the code for (fully connected) machine learning in this series of tutorials can be found in my neural networks GitHub repository at the following link.

https://github.com/mrdragonbear/Neural-Networks
No matter how much you understand about neural networks beforehand, I hope you enjoy reading this article and learn something new. Now, let’s get started!
Motivation for Neural Networks
A neural network that has not been trained is like a newborn baby: it knows nothing about the world (in terms of the blank slate theory) and can only gradually change its ignorance through exposure to the world, such as acquiring posterior knowledge. The algorithm perceives the world through data — we change its ignorance by training the neural network based on relevant datasets. In this process, the method we evaluate is by monitoring the errors produced by the neural network.
Before diving into the world of neural networks, it is important to understand the motivation behind them and how they work. To this end, we will briefly introduce logistic regression.
Regression is a method for modeling and predicting quantitative response variables (such as the number of taxi passengers or bike rentals), including ridge regression, LASSO, etc. When the response variable is categorical, this problem is no longer called a regression problem but is referred to as a classification problem.
Let’s consider a binary classification problem. The goal is to assign each observation to a category defined as Y based on a set of predictor variables X (such as a certain level or cluster).
For example, we might predict whether a patient has heart disease based on their characteristics. Here, the response variable is categorical, with a limited number of outcomes — more specifically, only two outcomes, as the response variable is binary (yes/no).
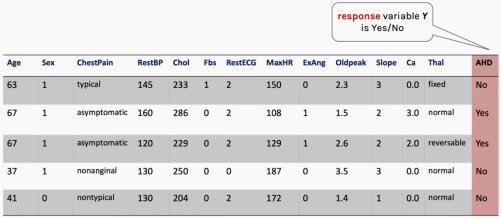
There are actually many features here, but we are currently only using MaxHR.
To make a prediction, we use logistic regression. Logistic regression solves this problem by estimating the probability P(y=1) that a patient has heart disease given the X value.
Logistic regression models P(y=1) using the logistic function:
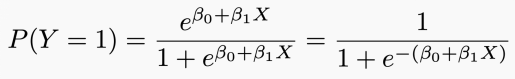
In this way, the model can predict P(y=1) using an S-shaped curve, which is the basic shape of the logistic function. β0 controls the right or left shift of the curve c=-β0/β1, while β1 controls the steepness of the S-shaped curve.
Note that if β1 is a positive number, the predicted value of P(y=1) changes from 0 to 1 as the X value increases; if β1 is a negative number, the relationship is reversed.
The graphical summary is as follows:
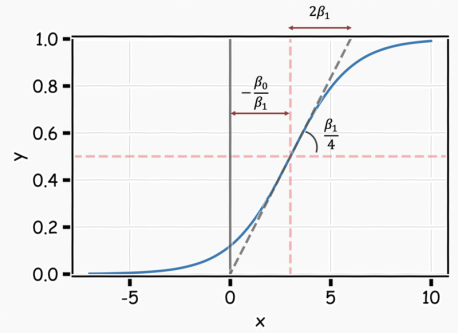
Now that we understand how to control the logistic regression curve, we can obtain the desired curve by adjusting some variables.
We can change β0 to shift the curve.
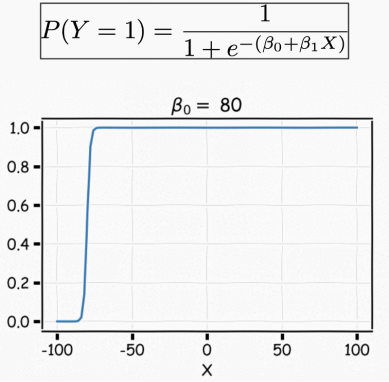
We can adjust β1 to change the gradient of the curve
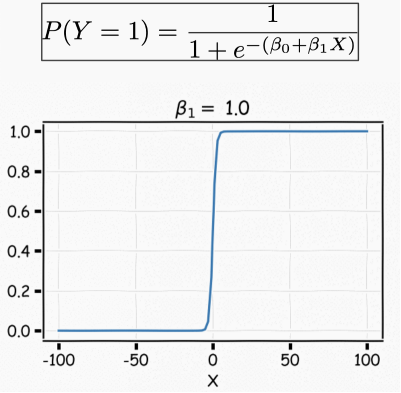
Doing this manually is tedious, and it is also difficult to adjust to the ideal values. To solve this problem, we use a loss function to quantify the level of residuals generated by the current parameters. We then seek the parameter values that minimize the loss function.
Thus, the parameters of the neural network are related to the errors generated by the network; when the parameters change, the errors also change. The optimization function we use to adjust the parameters is called gradient descent, which is very useful for finding the minimum of a function. We want to minimize the errors, which is also called the loss function or objective function.
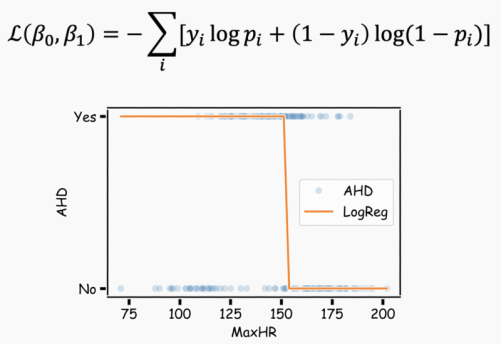
So what is the significance of all this, and how is it related to neural networks? In fact, what we are doing is fundamentally the same as what the neural network algorithm does.
In the previous model, we only used one feature; in a neural network, we can use multiple features. Each feature can have weights and error terms assigned, and these two parts combined are the regression parameters. Depending on whether the predicted result is a continuous variable or a categorical variable, the formulas may vary slightly.
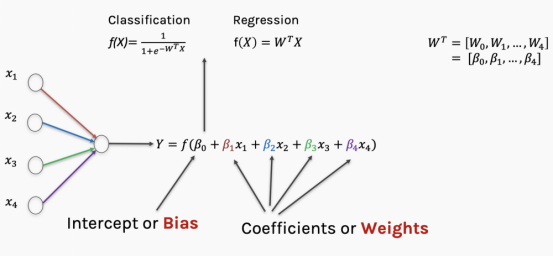
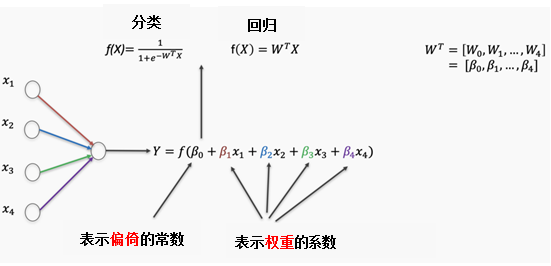
When we discuss the weights of a neural network, we are actually discussing the regression parameters of the incoming functions. The results of the incoming functions are passed to the activation function, which determines whether this result is sufficient to “ignite” the neural node. In the next article, I will discuss different types of activation functions in more detail.
Now we have established a simple neural network consisting of multiple logistic regressions and four features.
To begin updating and optimizing parameters, we need to start from some arbitrary value. We will evaluate the loss function after each update and perform gradient descent.
The first thing we need to do is set random weights. In our heart data, random weights are likely to perform poorly, leading the model to provide incorrect answers.
Then we “train” the network by penalizing the poorly performing network.
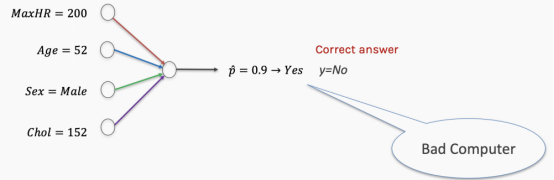
However, simply telling the computer whether its performance is good or bad is not very helpful. You need to tell it how to change these weights to improve the model’s performance.
We already know how to tell the computer that the network’s prediction performance is good; we just need to look at our loss function. But now this process is more complex because we have five weights to deal with. For now, I will consider only one weight, as this process is similar for all weights.
In an ideal scenario, we need to know what w will minimize ℒ(w).
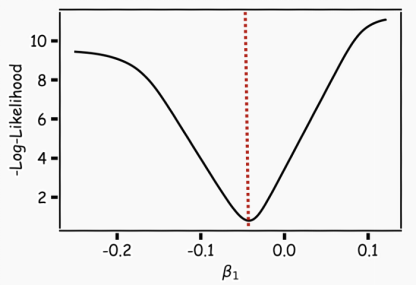
To find the optimal point of ℒ(w), we can differentiate ℒ(w) with respect to the weight w and set it to 0.
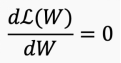
Then we need to find a w that satisfies this equation, but sometimes this problem does not have an explicit solution.
A more flexible approach is to choose an arbitrary starting point and determine in which direction to move to reduce the loss (in this case, whether to move left or right). Specifically, we can compute the slope of the function at this point. If the slope is negative, we move right; if the slope is positive, we move left. We then repeat this process until convergence.
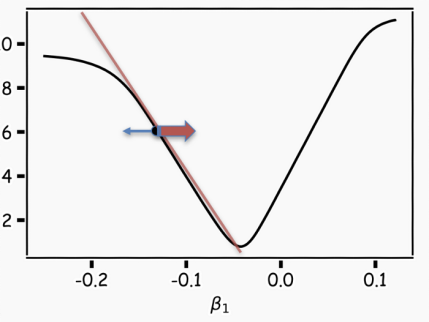
If the step size is proportional to the slope, we can avoid missing the minimum.
How do we perform such an iterative updating process? This is accomplished using a method called gradient descent, which has been briefly mentioned earlier.
Gradient Descent
Gradient descent is an iterative method for finding the minimum of a function. There are various methods of gradient descent, which I will discuss in detail in later articles. This blog introduces different methods for updating weights. Now, we will continue using the standard gradient descent algorithm, sometimes referred to as the delta rule.
We know to move in the opposite direction of the derivative (because we are trying to “move away” from the error) and want the step size to be proportional to the derivative. The step size is controlled by a parameter called the learning rate λ. Our new weights are the sum of the old weights and the new step size, where the step size is derived from the loss function, indicating how important the relevant parameters are in influencing the learning rate (and thus the derivative).


The larger the learning rate, the greater the weight of the derivative, and thus the step size for each iteration of the algorithm is larger. A smaller learning rate results in a smaller weight of the derivative, leading to a smaller step size for each iteration.
If the step size is too small, the algorithm will take a long time to converge; if the step size is too large, the algorithm will continually miss the optimal parameters. Clearly, the learning rate is an important parameter when building neural networks.
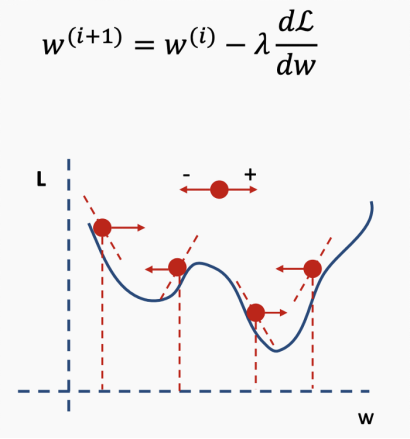
Gradient descent must consider several issues:
-
We still need to derive the derivative.
-
We need to know what the learning rate is or how to set it.
-
We need to avoid local minima.
-
Finally, the complete loss function includes the sum of all individual “errors.” This can be hundreds of thousands of functions like the one above.
Now the derivation of the derivative is done using automatic differentiation, so this is not a problem for us. However, deciding the learning rate is an important and complex issue that I will discuss in future tutorials.
Local minima are a very tricky problem for neural networks because the formulas of neural networks do not guarantee that we can reach the global minimum.
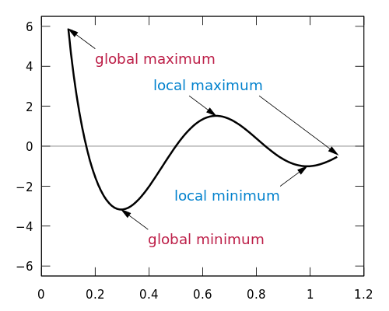
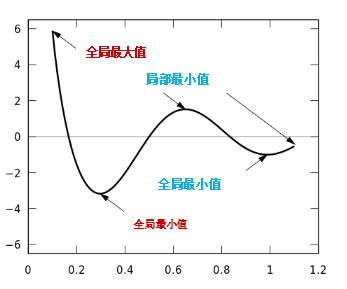
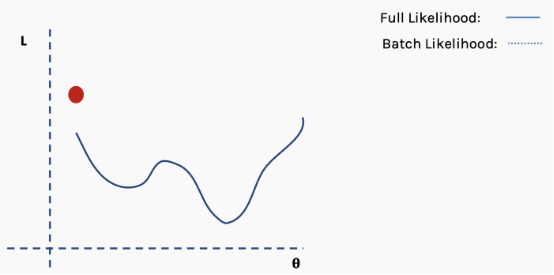
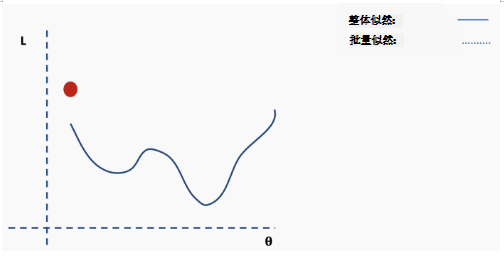
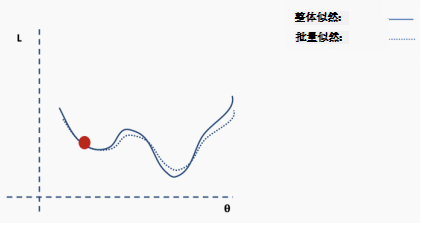
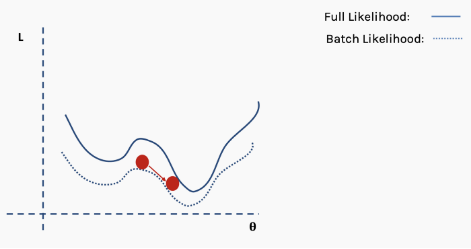
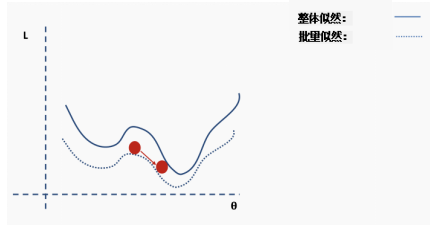
Getting trapped in local minima means we have only locally optimized the parameters, but there may be better solutions somewhere on the surface of the loss function. The loss surface of neural networks can have many such local optima, which is problematic for network optimization. For example, see the loss surface shown below.

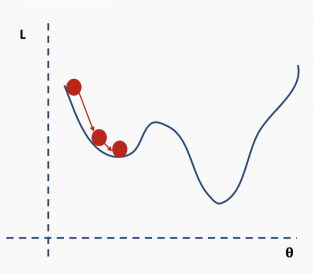
How do we solve this problem? One suggestion is to use batch and stochastic gradient descent. This idea sounds complicated, but it is actually quite simple — use a batch (a subset) of data instead of the entire dataset, so that the loss function’s surface will be partially deformed during each iteration.
For each iteration k, we can use the following loss (likelihood) function to derive the derivative:
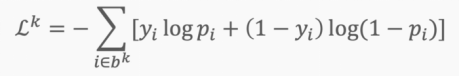
This is an approximation of the complete loss function. We can illustrate this with an example. First, we start with the surface of the complete loss (likelihood) function with randomly assigned network weights providing us with initial values.
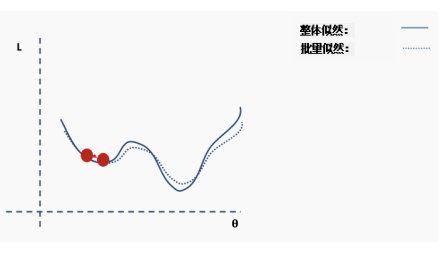
Then we choose a batch of data, perhaps 10% of the entire dataset, and construct a new loss function surface.
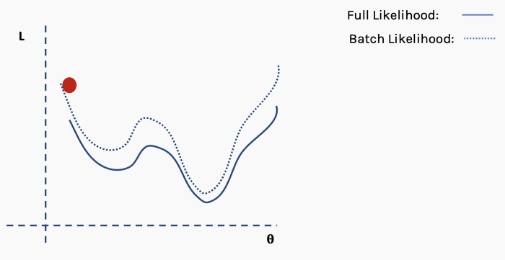
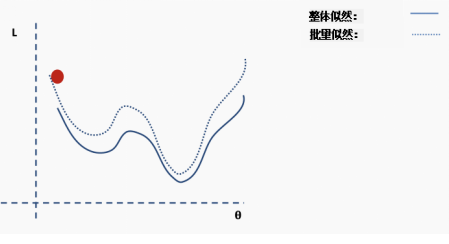
Then we perform gradient descent on this batch of data and update.
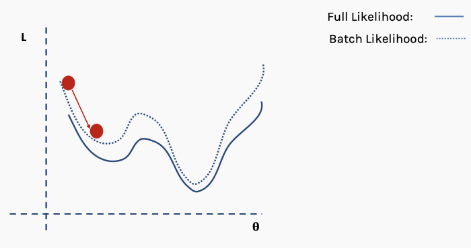
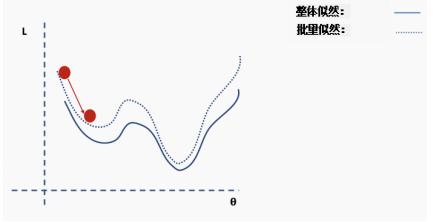
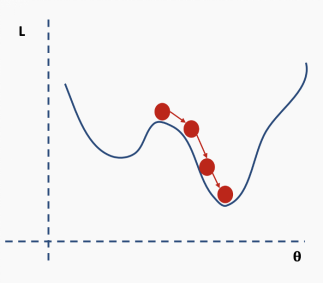
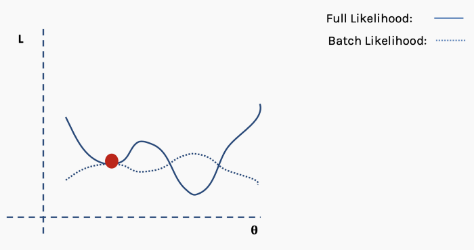
Now we are in a new position. Select a new random subset from the complete dataset, and then reconstruct the loss function surface.
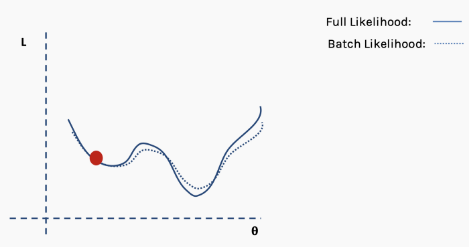
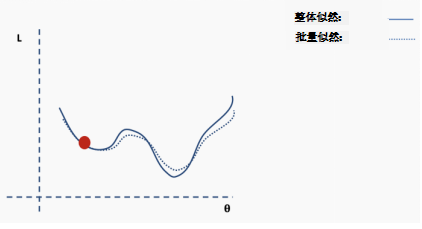
Then perform gradient descent and update on this batch of data.
Repeat the above process using new data.
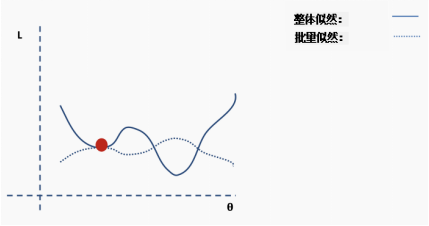
Perform the update.
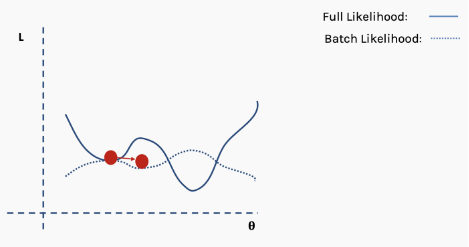
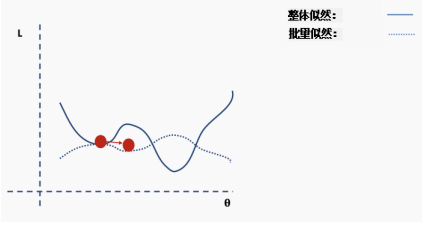
This process repeats for multiple iterations.
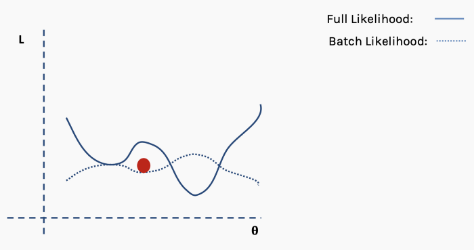
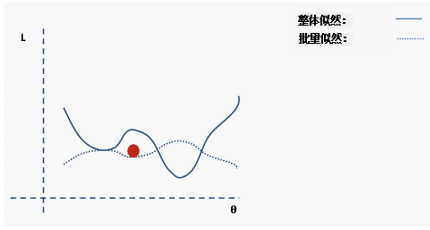
Until the network begins to converge to the global minimum.
Now we have enough knowledge in our toolkit to build our first neural network.
Artificial Neural Network (ANN)
We have learned how logistic regression works, how to evaluate network performance, and how to update the network to improve performance. Now we can start building a neural network.
First, I want everyone to understand why neural networks are called neural networks. You may have heard that this is because they mimic the structure of neurons, which are the cells in the brain. The structure of a neuron is much more complex than that of a neural network, but the functions are similar.

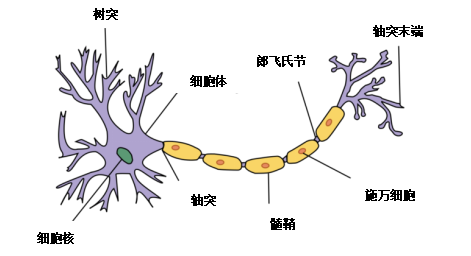
Real neurons work by accumulating potential; when it exceeds a certain value, it causes the presynaptic neuron to discharge through the axon and stimulate the postsynaptic neuron.
Humans have billions of interconnected neurons that can produce extremely complex discharge patterns. The functioning of the human brain is incredible compared to what our most advanced neural networks can do. Therefore, we are unlikely to see neural networks mimicking the functions of the human brain anytime soon.
We can draw a neural diagram to compare the structure of neurons in neural networks with artificial neurons.
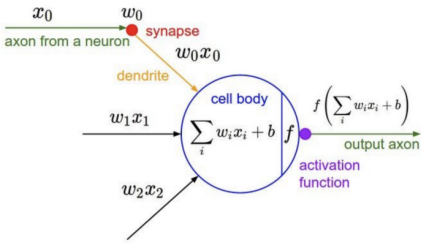
Source
Considering the capabilities of the human brain, it is clear that the range of capabilities of artificial neural networks is infinite — especially as we begin to connect them with sensors, actuators, and the wealth of information on the Internet — this explains the popularity of neural networks in the world, even though they are still in a relatively early stage of development.
After all, reductionists might argue that humans are merely a collection of neural networks connected to sensors and actuators through various parts of the nervous system.
Now suppose we have multiple features. Each feature is passed through something called an affine transformation, which is essentially an addition (or subtraction) and/or multiplication. This forms something akin to a regression equation. When multiple nodes in a multilayer perceptron converge on one node, the affine transformation becomes important.
Then we pass this result through an activation function, which gives us some form of probability. This probability determines whether the neuron will fire — the result can be incorporated into the loss function to evaluate the performance of the algorithm.
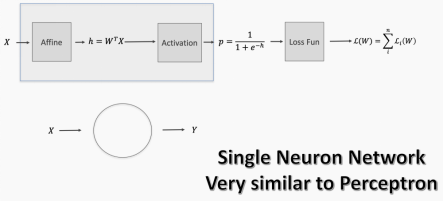
From now on, I will abstract the affine and activation modules into one module. However, we must understand that the affine transformation is the merging of outputs from upstream nodes, and then the total output is passed to an activation function, which determines whether it is sufficient to stimulate the neuron.
Now we can return to the first example using heart disease data. We can take two logistic regressions and combine them. A single logistic regression is as follows:
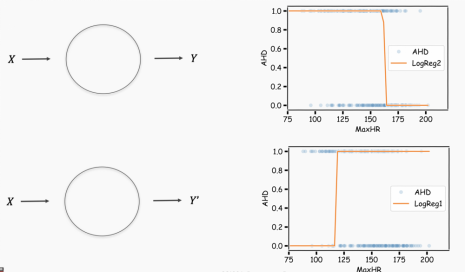
When we connect these two networks, we obtain a network with greater flexibility due to the increase in degrees of freedom.
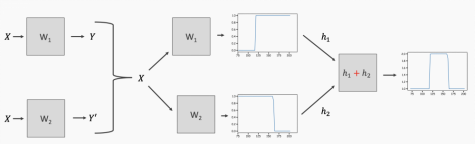
This illustrates the functionality of neural networks well; we are able to chain multiple functions together (sum), resulting in a large number of functions (from a large number of neurons), thus producing highly nonlinear functions. With enough neurons, we can produce arbitrarily complex continuous functions.
This is a very simple example of a neural network; however, we still encounter a problem: even with such a simple network, how do we update the weight values?
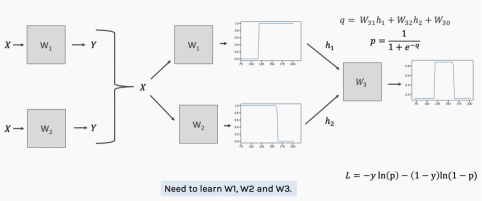
We need to be able to calculate the derivative of the loss function with respect to these weights. To solve for the unknown weights w1, w2, and w3, we need to use backpropagation.
Backpropagation
Backpropagation is the core mechanism of learning in neural networks. It is the messenger that tells the network whether it made an error during prediction. The discovery of backpropagation is one of the most significant milestones in the entire study of neural networks.
Propagation is the transfer of something in a specific direction or through a specific medium (such as light or sound). When we discuss backpropagation in the context of neural networks, we are discussing the transmission of information related to the errors generated when the neural network guesses the data.
During the prediction process, the neural network propagates signals forward through the nodes of the network until it reaches the output layer that makes the decision. Then, the network backpropagates the information about this prediction error to change each parameter.
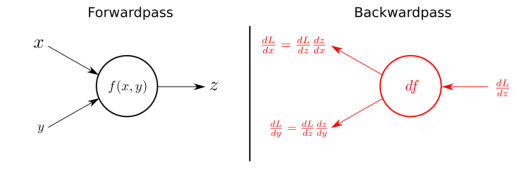
Backpropagation is the method for calculating the derivative of each parameter in the network, which is necessary for performing gradient descent. This is a crucial distinction between backpropagation and gradient descent, as the two can easily be confused. We first perform backpropagation to obtain the information needed to execute gradient descent.
You may have noticed that we still need to calculate derivatives. Computers cannot distinguish, but we can build a function library to do this without the involvement of the network designer, abstracting this process, which is called automatic differentiation. Here is an example.
We can do this manually, and then change it based on different network architectures and nodes.
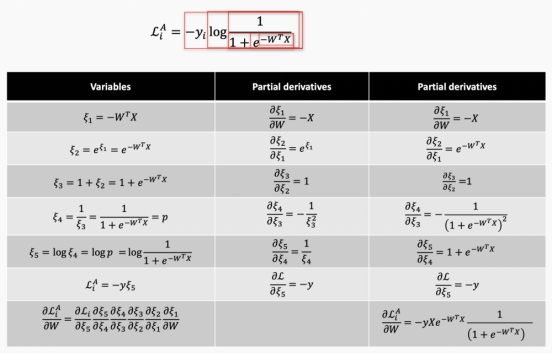
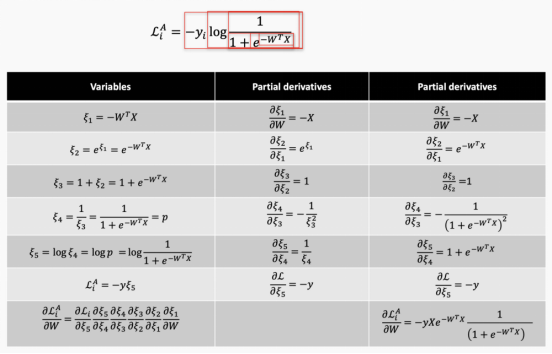
Or, we can write a function library that has internal links with the architecture so that when the network architecture is updated, the process is abstracted and automatically updated.

If you really want to understand how practical this abstract automatic differentiation process is, try creating a multilayer neural network with six nodes and then write code to implement backpropagation (if anyone has the patience and courage to do so, kudos to you).
More Complex Networks
For most applications, a network with two nodes is not particularly useful. Typically, we use neural networks to approximate complex functions that are difficult to describe using traditional methods.
Neural networks are special because they follow what is known as the universal approximation theorem. This theorem states that in a neural network, given an infinite number of neurons, any complex continuous function can be precisely represented. This is a rather profound statement, as it means that, given enough computational power, we can essentially approximate any function.
Clearly, in practice, this idea has several issues. First, we are limited by the existing data, which restricts the potential accuracy of our predicted categories or estimated values. Secondly, we are limited by computational power. Designing a network that far exceeds the capabilities of the world’s most powerful supercomputers is quite easy.
The solution to this problem is to design a network architecture that allows us to achieve high accuracy with relatively little computational power and minimal data.
Even more impressively, a single hidden layer is sufficient to represent an arbitrary precision function approximation.
So if one layer is enough, why do people use multilayer neural networks?
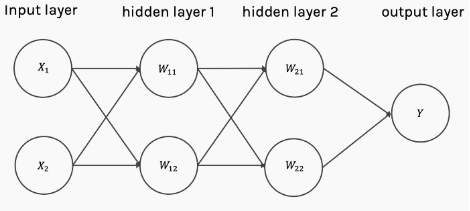
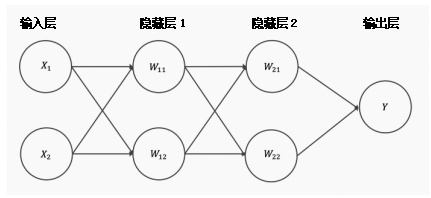
Neural structures with multiple hidden layers
The answer is simple. A network with only one layer requires a very wide neural structure because shallow networks require (exponentially) more width than deep networks. Additionally, shallow networks are more prone to overfitting.
This is the reason for the emergence and development of deep learning (where deep refers to multiple layers of neural networks), which dominates contemporary research literature in machine learning and most fields involving data classification and prediction.
Summary
This article discussed the motivation and background of neural networks and outlined how to train neural networks. We discussed loss functions, error propagation, activation functions, and network architectures. The following diagram summarizes all the concepts discussed and how they relate to each other.
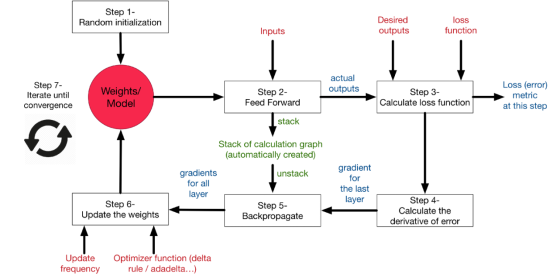
The knowledge in this article will provide a strong foundation for further discussions on how to improve the performance of neural networks and apply them in deep learning applications.
Original Title:
Introduction to Neural Networks
Original Link:
https://towardsdatascience.com/simple-introduction-to-neural-networks-ac1d7c3d7a2c
Editor: Yu Tengkai
Proofreader: Lin Yilin
Translator’s Bio
Chen Dan, a junior at Fudan University, majoring in preventive medicine and minoring in data science. Passionate about data analysis but just entering this field, there is still a lot of space for improvement. I hope to expand my reading of literature and learn more cutting-edge knowledge while working in the translation team, and also meet more like-minded friends!
Recruitment Information for the Translation Team
Job Description: A meticulous heart is needed to translate selected foreign articles into fluent Chinese. If you are an international student in data science/statistics/computer science, or working overseas in related fields, or confident in your language skills, you are welcome to join the translation team.
What You Will Gain: Regular translation training to improve volunteers’ translation skills, enhance understanding of cutting-edge data science, and overseas friends can stay connected with domestic technological development. The background of THU Data Team provides good development opportunities for volunteers.
Other Benefits: You will have the opportunity to work with data scientists from well-known companies, students from Peking University, Tsinghua University, and other prestigious institutions.
Click on the “Read Original” at the end of the article to join the Data Team~
Note on Reproduction
If you need to reproduce, please indicate the author and source prominently at the beginning (transferred from: Data Team ID: datapi), and place a prominent QR code of the Data Team at the end of the article. For articles with original identification, please send [Article Name – Name and ID of the Authorized Public Account] to the contact email to apply for whitelist authorization and edit as required.
After publication, please feedback the link to the contact email (see below). Unauthorized reproduction and adaptation will be legally pursued.


Click “Read Original” to embrace the organization