Click the above “Beginner Learning Visuals” to choose to add a “Star” or “Pinned”
Heavyweight content delivered first-hand
Source:getwallpapers.com
Deep learning is one of the important branches of machine learning. Its goal is to teach computers to perform tasks that are quite natural for humans. Deep learning is also a key technology behind autonomous vehicles, helping them recognize stop signs and differentiate between pedestrians and lamp posts. It is crucial for enabling voice control in devices such as smartphones, tablets, televisions, and hands-free speakers. Recently, deep learning has gained widespread attention for its unprecedented results.
In deep learning, computer models learn directly how to perform classification tasks from images, text, or sound. Deep learning models can achieve the highest accuracy, sometimes even surpassing human levels. We typically use a large amount of labeled data and neural network architectures containing many layers to train models.
Resources
Deep learning models can be applied to various complex tasks:
1. Artificial Neural Networks (ANN) for regression and classification
2. Convolutional Neural Networks (CNN) for computer vision
3. Recurrent Neural Networks (RNN) for time series analysis
4. Self-Organizing Maps for feature extraction
5. Deep Boltzmann Machines for recommendation systems
6. Autoencoders for recommendation systems
In this article, we will introduce all relevant content about Artificial Neural Networks (ANN) as much as possible.
“Artificial Neural Networks (ANN) are a paradigm of information processing inspired by the way biological neural systems (the brain) process information. They consist of a large number of highly interconnected processing elements (neurons) that work together to solve specific problems.”
Main Content:
1. Neurons
2. Activation Functions
3. Types of Activation Functions
4. How Neural Networks Work
5. How Neural Networks Learn (Backpropagation)
6. Gradient Descent
7. Stochastic Gradient Descent
8. Training Neural Networks with Stochastic Gradient Descent
Neurons
Neurons (also known as nerve cells) are the basic units of the brain and nervous system, receiving stimulus information from the external world through dendrites, processing that information, and then outputting it to other cells through axons.
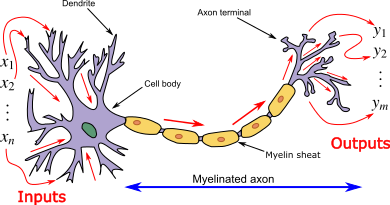
Biological Neurons
Cell Body (Soma): The main part of the neuron cell, containing the nucleus, where necessary biochemical reactions occur.
Dendrites: Hair-like tubular structures surrounding the neuron. They are primarily responsible for receiving input signals.
Axon: A long tubular structure, similar to a transmission line.
Synapses: Neurons connect with each other in a complex spatial arrangement. The terminal end of the axon branches again, forming a highly complex and specialized structure known as a synapse. Connections between two neurons occur at these synapses.
Dendrites receive input information from other neurons. The cell body processes this incoming information and produces an output result, which is sent to other neurons through the axon and synapse.
Electrical signals flow through neurons.
The following diagram represents a general model of ANN inspired by biological neurons. It is also known as a perceptron.
A single-layer neural network is generally referred to as a perceptron; given an input, it will compute an output.
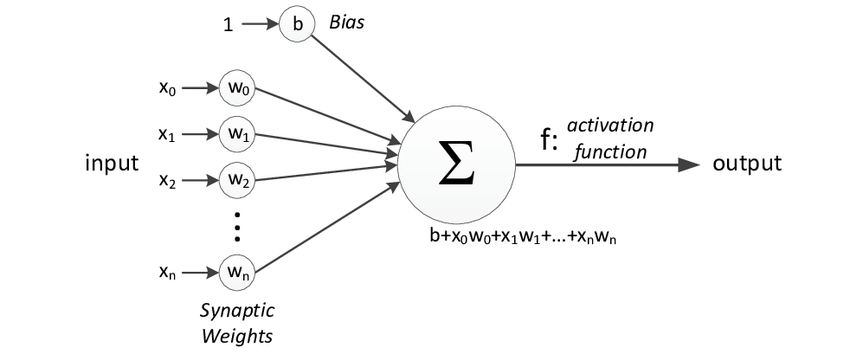
Perceptron
In the above image, x0, x1, x2, x3…x(n) represent the inputs to the network (independent variables), each input is multiplied by the corresponding weight when passing through the so-called dendrites. The weights are represented as w0, w1, w2, w3….w(n), showing the strength of specific nodes.b is the bias value. The bias value can shift the activation function upward or downward.
In the simplest case, these products are summed and input into a transfer function (activation function) to obtain the result, which is then sent as output.
Activation Functions
Activation functions are crucial for ANN to learn and understand truly complex things. Their primary purpose is to convert the input signals of nodes in ANN into output signals, which will serve as inputs for the next layer.
Activation functions determine whether a neuron should be activated by calculating the weighted sum and bias. The goal is to introduce non-linearity.
If we do not apply an activation function, the output signal will merely be a linear function (a first-degree polynomial). Linear functions are easy to solve, and the power consumption is relatively low, but their complexity is limited. Therefore, without activation functions, our model cannot learn or model complex data such as images, videos, audio, speech, etc.
Why do we need non-linear functions?
Non-linear functions are functions with curvature. Now we need neural networks to learn and represent any complex function that maps inputs to outputs. Therefore, neural networks are also considered “universal function approximators.”
Types of Activation Functions:
1. Threshold Activation Function – (Binary Step Function)
The binary step function is a threshold-based activation function. If the input value exceeds a certain threshold, the neuron is activated and sends the same signal to the next layer; if below a certain threshold, it is not activated.
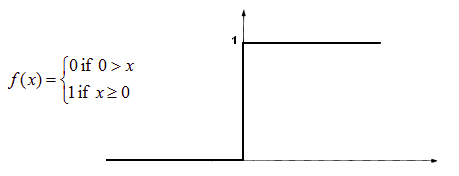
Binary Function
The problem with this function is creating a binary classifier (1 or 0), but if we want to connect multiple such neurons to introduce more classes, like Class1, Class2, Class3, etc., in this case, all neurons will give 1, and we will be unable to make judgments.
2. Sigmoid Activation Function – (Logistic Function)
The sigmoid function is a mathematical function with a characteristic “S” shaped curve, ranging from 0 to 1, thus used for predicting probabilities as output.
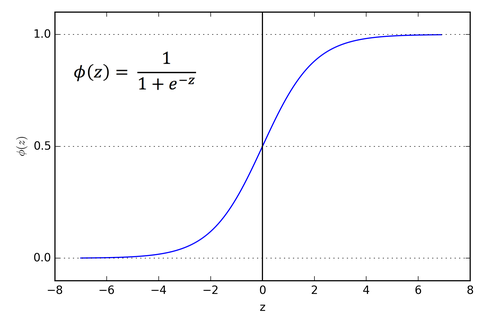
Sigmoid Curve
The sigmoid function is differentiable, meaning we can solve the slope of the curve between any two points. A disadvantage of the sigmoid activation function is that it may cause the neural network to get stuck during training if provided with large negative inputs.
3. Hyperbolic Tangent Function – (tanh)
Similar to sigmoid but performs better. It is essentially non-linear, allowing us to stack layers. The range of this function is (-1, 1).
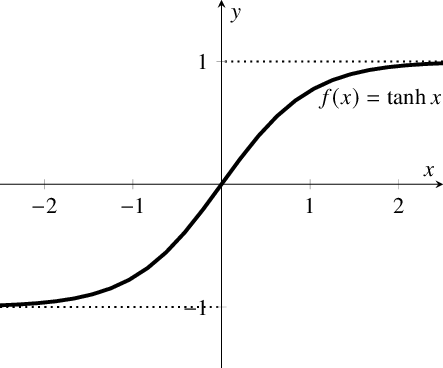
Hyperbolic Tangent Function
The main advantage of this function is that negative inputs map to negative outputs, and only zero input is mapped to an output close to zero. Thus, the chance of getting stuck during training is lower.
4. Rectified Linear Unit – (ReLu)
ReLu is the most commonly used activation function in CNN and ANN, ranging from zero to infinity [0, ∞].
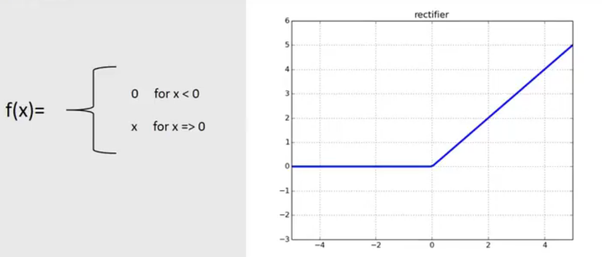
ReLu
If x is positive, the output is “x”; if x is negative, the output is 0. ReLu appears to be a linear function problem, but it is essentially non-linear, and combinations of ReLu are also non-linear. In fact, it is a good approximator that can approximate most functions through combinations of ReLu.
It is generally applied to the hidden layers of neural networks. For the output layer, softmax function is typically used for classification problems, while linear function is used for regression problems.
One issue here is that some gradients may vanish during training. This can lead to weight updates where no data point activates that neuron. ReLu essentially causes neurons to die.
To solve this problem, Leaky ReLu was introduced. Leaky ReLu introduces a small slope to ensure that the aforementioned problem does not occur. Leaky ReLu ranges from -∞ to +∞.
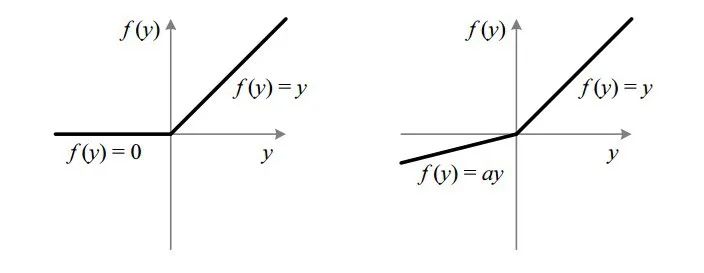
ReLu vs Leaky ReLu
Leaky increases the output range of the ReLu function. Typically, a = 0.01. When a is not 0.01, it is referred to as Random ReLu.
How Neural Networks Work?
Let’s take real estate prices as an example. First, we will summarize different factors into one line of data: Area, Bedrooms, Distance to city and Age.

Input values reach the output layer directly through weighted synapses. All four input values are analyzed and input into the activation function to produce an output result.
This is simple, but by adding a hidden layer between the input and output layers, we can expand the functionality of the neural network and improve its accuracy.
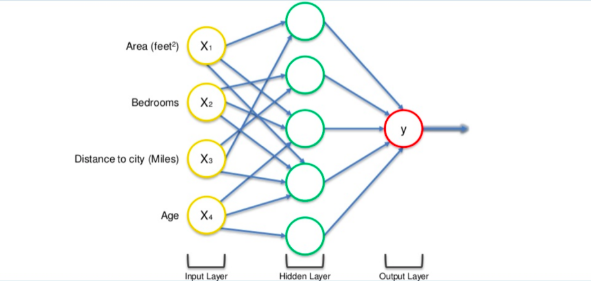
Neural Network with Hidden Layers (only showing non-zero values)
Now in the above image, all four variables are connected to the neuron through synapses. However, not all synapses are weighted. The weights include zero and non-zero values. Here, non-zero values indicate importance, while zero values indicate that the input is discarded.
Let’s take the first neuron as an example, where Area and Distance to City are non-zero, indicating they are important to the first neuron. The other two variables, Bedrooms and Age, have weights of 0, thus not passing through the first neuron.
You might wonder why the first neuron only considers two of the four variables. The further away from the city, the cheaper the house becomes, which is common in the real estate market. Thus, what this neuron does may be to look for houses closer to the city.
There are many neurons, and each neuron performs similar calculations with different combinations of these variables. Once the criteria are met, the neuron will compute using the activation function.
The next neuron’s weighted synapses might be Distance to the city and Bedrooms. Thus, neurons work in a very flexible manner, searching comprehensively to find specific things.
How Neural Networks Learn?
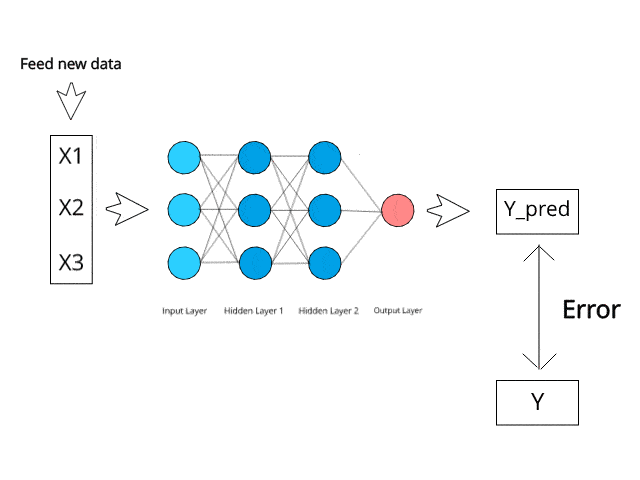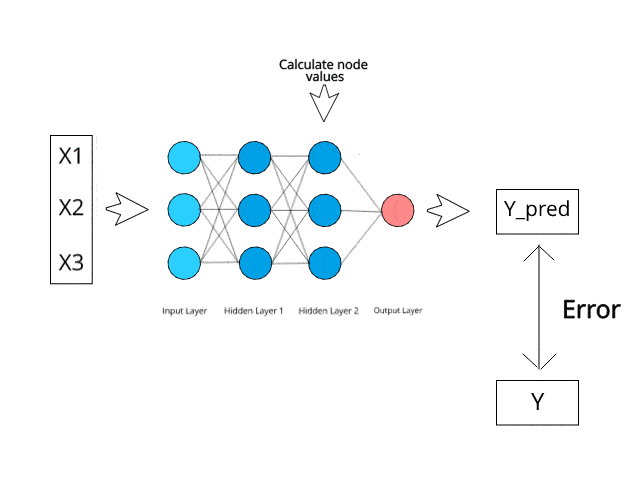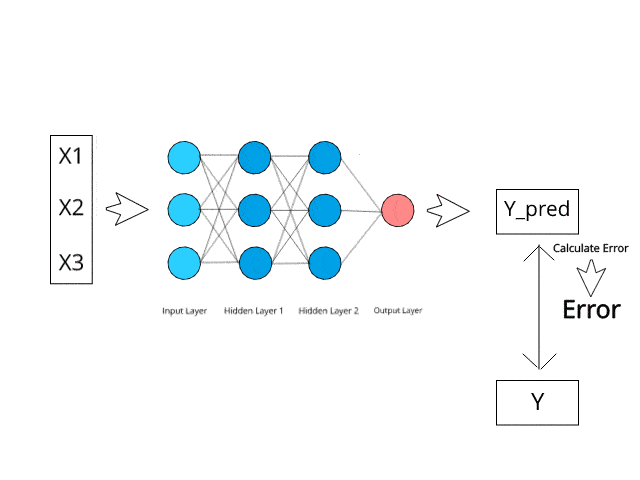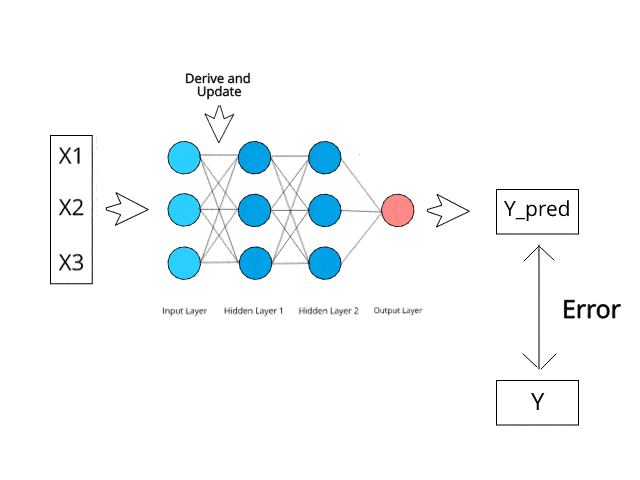
Let’s first make an analogy. The learning of neural networks is closely related to our normal learning process. We first complete a certain task and receive corrections from a coach, then complete the task better next time. Similarly, neural networks need trainers to describe the network’s response to inputs. Using the difference between actual values and predicted values, an error value (also known as the cost function) is calculated and sent back to the system.
Cost Function: Half of the squared difference between actual values and output values.
For each layer of the network, the cost function is analyzed, and it adjusts the thresholds and weights for the next input. Our goal is to minimize the cost function. The lower the cost function, the closer the actual values are to the predicted values. Thus, as the network continues to learn, the error for each run decreases.
We feedback result data through the entire neural network. Connecting input variables to the weighted synapses of neurons is the only thing we can control. Thus, as long as there is a difference between actual values and predicted values, we need to adjust the weights. Once we slightly adjust them and run the neural network again, a new cost function will be generated, which we hope will be smaller than the previous one. This process is repeated until the cost function is minimized as much as possible.
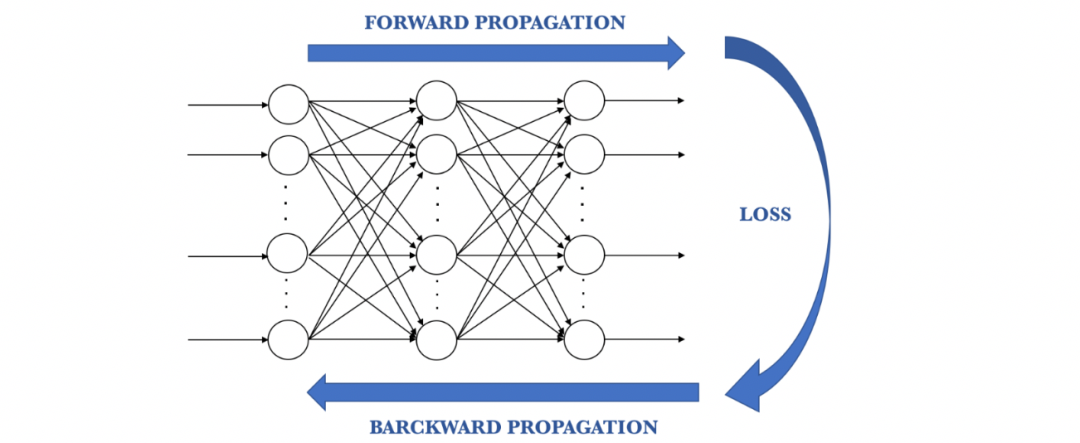
The above process is called backpropagation, and it continues through the network until the error value is kept at a minimum.
Backpropagation
There are two methods for adjusting weights:1. Brute Force Method2. Batch Gradient Descent
Brute Force Method
This is suitable for single-layer feedforward networks. Here, we need to consider many possible weights. In this method, we want to discard all other weights except for the U-shaped curve bottom weight. The optimal weight can be found using simple elimination techniques. This method is effective if we only need to optimize one weight. However, if it is a complex neural network with many weights, this method will be impractical due to high dimensionality.
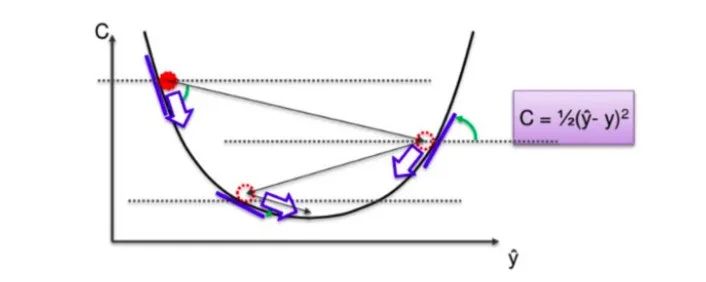
Batch Gradient Descent
It is a first-order iterative optimization algorithm that finds the minimum cost (loss) value during the training of models with different weights.
Gradient Descent
In the “gradient descent” process, we do not look at each weight at once and eliminate incorrect weights, but we look at the slope of the function.
If the slope→negative, it indicates that you are descending along the curve.If the slope→positive, do nothing
This way, a large number of incorrect weights can be eliminated.
Stochastic Gradient Descent (SGD)
As shown in the above image, gradient descent works well when we have a convex curve. However, if we do not have a convex curve, gradient descent will fail.
“ Stochastic ” refers to systems or processes related to random probabilities. In stochastic gradient descent, a few samples are randomly selected instead of the entire dataset for each iteration.
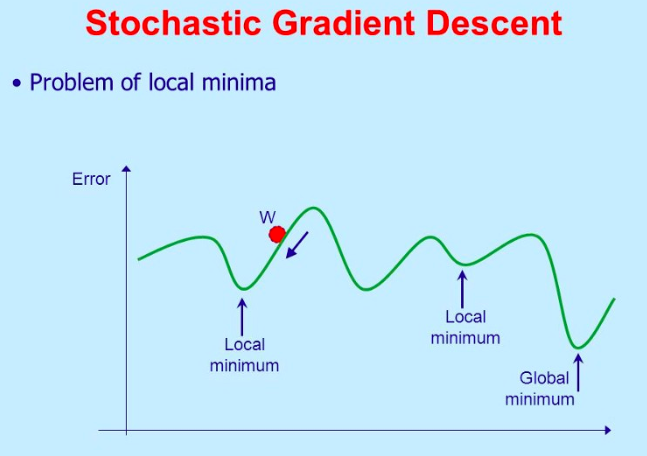
Stochastic Gradient Descent
In SGD, we take one row of data at a time, run that data through the neural network, and then adjust the weights. For the second row, we run it, compare the Cost function, and then adjust the weights again.
SGD helps us avoid the problem of local minima. It is much faster than Gradient Descent because it runs each row at a time and does not need to load the entire data into memory for computation.
One thing to note is that since SGD is usually noisier than typical Gradient Descent due to its randomness in descent, it generally requires more iterations to reach the minimum. Although it requires more iterations to reach the minimum compared to typical Gradient Descent, it still consumes much less computation than typical Gradient Descent. Therefore, in most cases, SGD outperforms batch gradient descent.
Training Neural Networks with Stochastic Gradient Descent
Step 1→ Randomly initialize weights to small decimals close to 0 but not 0.
Step 2→ Input the first observation of the dataset into the input layer, placing each feature in a node.
Step 3→ Forward Propagation: From left to right, neurons are activated sequentially until a predicted value is obtained. The influence of each neuron is limited by the weights.
Step 4→ Compare the predicted result with the actual result and measure the error (cost function).
Step 5→ Back Propagation: From right to left, the error is propagated backward. Weights are updated according to their impact on the error. The learning rate determines the extent to which we update the weights.
Step 6→ Repeat Steps 1 to 5, updating weights after each comparison (Reinforcement Learning)
Step 7→ When the entire training set has passed through the ANN, it is complete.
Conclusion
Source:techcrunch.com
Neural networks are a brand new concept with great potential. They can be applied to various different concepts and learn through specific backpropagation and error correction mechanisms during the testing phase. These multi-layer systems may one day reduce the likelihood of errors solely through learning, without the need for manual correction.
If this article helps you, please consider giving a “triple-click” at the end.

Discussion Group
Welcome to join the reader group of the public account to communicate with peers. Currently, there are WeChat groups for SLAM, 3D Vision, Sensors, Autonomous Driving, Computational Photography, Detection, Segmentation, Recognition, Medical Imaging, GAN, Algorithm Competitions, etc. (will gradually be subdivided in the future). Please scan the WeChat ID below to join the group, with remarks: “nickname + school/company + research direction”, for example: “Zhang San + Shanghai Jiao Tong University + Visual SLAM”. Please do not send advertisements in the group, otherwise you will be removed. Thank you for your understanding~