Understanding CNNs from the Frequency Domain Perspective

Click on the above “Beginner’s Guide to Vision“, choose to add “Star Mark” or “Pinned“

Important insights delivered promptly

For academic sharing only, does not represent the stance of this public account. Contact us for removal in case of infringement.

Reprinted from: This article is compiled from Zhihu Q&A. Infringement will be removed.

Editor丨Jishi Platform

Understanding CNNs from the Frequency Domain Perspective

Viewpoint One

Author丨Ruoyu

I think the most enlightening work for me is by Xu Zhiqin from Shanghai Jiao Tong University.

https://ins.sjtu.edu.cn/people/xuzhiqin/fprinciple/index.html

His Bilibili speech:

https://www.bilibili.com/video/av94808183?p=2

Additionally, I have heard him speak offline about two times, almost always discussing neural networks in relation to Fourier transforms and Fourier analysis.

Training behavior of deep neural network in frequency domain

https://arxiv.org/pdf/1807.01251.pdf

This paper clearly states that the generalization performance of neural networks comes from their training process, which focuses more on low-frequency components.

The fitting process of neural networks on CIFAR-10 and MNIST, with blue representing low frequency and red representing high frequency, shows that as training approaches convergence, the low-frequency components that need to be learned decrease.

Theory of the frequency principle for general deep neural networks

https://arxiv.org/pdf/1906.09235v2.pdf

A large amount of mathematical derivation is done to prove the F-Principle, divided into the initial, middle, and concluding stages of training, which can be somewhat tedious for non-mathematics majors.

Explicitizing an Implicit Bias of the Frequency Principle in Two-layer Neural Networks

https://arxiv.org/pdf/1905.10264.pdf

Why deep neural networks (DNNs) with more parameters than samples can usually generalize well remains a mystery. One attempt to understand this issue is to discover the implicit bias during the training process of DNNs, such as the frequency principle (F-Principle), which states that DNNs typically fit target functions from low frequency to high frequency. Inspired by the F-Principle, this paper proposes an effective linear F-Principle dynamic model that accurately predicts the learning outcomes of wide two-layer ReLU neural networks (NNs). This Linear FP dynamics is rationalized by the linearized Mean Field residual dynamics of NNs. Importantly, the long-time limit solution of this LFP dynamics is equivalent to the solution of a constrained optimization problem that explicitly minimizes the FP norm, where feasible solutions are more severely penalized for high frequencies. Using this optimization formula, a prior estimate of the generalization error bound is provided, indicating that the higher the FP norm of the target function, the larger the generalization error. Overall, by interpreting the implicit bias of the F-Principle as an explicit penalty for two-layer NNs, this work makes progress towards quantitatively understanding the learning and generalization of general DNNs.

This is a schematic diagram of the LFP model for two-dimensional data in images.

Professor Xu’s previous introduction:

The LFP model provides a new perspective for the quantitative understanding of neural networks. Firstly, the LFP model effectively characterizes the key features of the training process of a highly parameterized system like neural networks using a simple differential equation and can accurately predict the learning outcomes of neural networks. Therefore, this model establishes a relationship between differential equations and neural networks from a new angle. Since differential equations are a very mature research field, we believe that tools from this field can help us further analyze the training behavior of neural networks. Secondly, similar to statistical physics, the LFP model is only related to some macroscopic statistics of network parameters and is independent of the specific behavior of individual parameters. This statistical characterization can help us accurately understand the learning process of DNNs when there are many parameters, thereby explaining the good generalization ability of DNNs when the parameters far exceed the number of training samples. In this work, we analyze the evolution results of this LFP dynamics through an equivalent optimization problem and provide a prior estimate of the network’s generalization error. 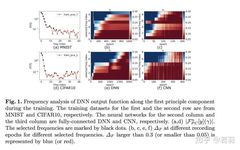We found that the generalization error of the network can be controlled by a kind of F-principle norm (defined as Understanding CNNs from the Frequency Domain Perspective

, γ(ξ) is a weight function that decays with frequency).

It is worth noting that our error estimation targets the learning process of the neural network itself and does not require adding extra regularization terms in the loss function. We will further elaborate on this error estimation in subsequent articles.

FREQUENCY PRINCIPLE: FOURIER ANALYSIS SHEDS LIGHT ON DEEP NEURAL NETWORKS

https://arxiv.org/pdf/1901.06523.pdf

This indicates that for any two non-converging frequencies, the low-frequency gradient performs exponentially better than the high-frequency gradient under smaller weights. According to Parseval’s theorem, the MSE loss in the spatial domain is equivalent to the L2 loss in the Fourier domain. To intuitively understand the high decay rate of the low-frequency loss function, we consider training in the Fourier domain of a loss function with only two non-zero frequencies.

It explains why the ReLU function works because the tanh function is smooth in the spatial domain, and its derivative decays exponentially with frequency in the Fourier domain.

Professor Xu’s popular science articles on the F-Principle:

https://zhuanlan.zhihu.com/p/42847582

https://zhuanlan.zhihu.com/p/72018102

https://zhuanlan.zhihu.com/p/56077603

https://zhuanlan.zhihu.com/p/57906094

On the Spectral Bias of Deep Neural Networks

The work of the Bengio group previously wrote a rough analysis note:

https://zhuanlan.zhihu.com/p/160806229

1. Analyzing the Fourier spectral components of ReLU networks using a continuous piecewise linear structure.

2. Discovering empirical evidence of spectral bias originating from low-frequency components, however, learning low-frequency components helps the network’s robustness against interference.

3. Providing a theoretical framework for learning analysis through manifold theory.

Based on the topological Stokes theorem, it is proved that the ReLU function is compact and smooth, aiding the convergence of training. What about the subsequent Swish and Mish? (Dog head).

Thus, in high-dimensional space, the spectral decay of the ReLU function has strong anisotropy, and the upper limit of the amplitude of the ReLU Fourier transform satisfies the Lipschitz constraint.

Experiments:

Center Point: High priority for learning low-frequency components

Conducting experiments on functions:

Fourier transform effects

Iterative process of learning the function

Standardized spectral components of the model

2. Learning MNIST data in a noisy environment

Different validation losses

Frequency components of MNIST data fitting

Neural networks can approximate arbitrary value functions, but researchers found that they prefer low-frequency components, thus exhibiting a bias towards smooth functions—this phenomenon is known as spectral bias.

Manifold Hypothesis

The more complex the manifold, the easier the learning process becomes. This hypothesis may break the “structural risk minimization” assumption, potentially leading to overfitting.

If there is a complex dataset (ImageNet), the search space is relatively large, and methods must be employed to make it “work in harmony” and tune it to work.

It seems that Bengio believes it has implications for the regularization of deep learning.

Machine Learning from a Continuous Viewpoint

https://arxiv.org/pdf/1912.12777.pdf

Mathematician Wienan.E’s debate shows that the frequency principle does not always work.

Assuming a certain function:

Probability measure

Based on kernel functions to derive:

Where:

Decomposing the Fourier coefficients:

Derived:

Characteristic function:

Then gave the boundaries where the frequency principle works.

Conditions for working:

Conditions for not working:

If Wienan.E provided the boundaries of the Frequency Principle from a mathematician’s perspective, then engineering colleagues must take a look at this paper:

A Fourier Perspective on Model Robustness in Computer Vision

https://arxiv.org/pdf/1906.08988.pdf

The code has also been open-sourced:

https://github.com/google-research/google-research/tree/master/frequency_analysis

The author’s intention is to focus on robustness and not completely discard high-frequency features.

Image description translation: Using input information that humans cannot recognize, the model can achieve high accuracy. The above shows the models that have been trained and tested, which applied strict high-pass and low-pass filtering at the input end. Through positive low-pass filtering, when the image looks like a simple colored sphere, the model still exceeds 30% accuracy on ImageNet. In the case of high-pass (HP) filtering, using input features that are almost invisible to humans, the model can achieve over 50% accuracy. As shown on the right, normalization processing is required for high-pass filtered images to visualize high-frequency features correctly (we use the method provided in the appendix to visualize high-pass filtered images).

Image description translation: Left: Fourier spectrum of natural images; we estimate E[|F(X)[i,j]|] by averaging all CIFAR-10 validation images. Right: Fourier spectrum of corrupted images with severity 3 in CIFAR-10-C. For each corruption, we estimate E[|F(C(X)−X)[i,j]|] by averaging all validation images. Additive noise has a higher concentration in the high-frequency band, while fog, contrast, and other pollution concentrate in the low-frequency band.

Image translation description: Model sensitivity to additive noise from different Fourier basis vectors on CIFAR-10. We fixed the additive noise to “L2 norm of 4” and evaluated three models: natural training model, adversarial training model, and Gaussian data augmentation training model. The average error rate was obtained from 1000 random samples of images from the test set. In the bottom row, we show images affected by noise along the corresponding Fourier basis vectors. The natural training model is highly sensitive to all additive noise except for the lowest frequency. Both adversarial training and Gaussian data augmentation greatly enhance robustness against high frequencies, while sacrificing the natural training model’s robustness at low frequencies (i.e., the middle blue area in these two models is smaller than that of the natural training model).

Image translation description: Sensitivity of models to additive noise of different Fourier basis vectors on ImageNet validation images. We fixed the basis vector to an L2 norm value of 15.7. The error rate is the average error rate over the entire ImageNet validation set. A 63×63 square is centered around the lowest frequency of the Fourier domain. Similarly, the natural training model is highly sensitive to all additive noise except for the lowest frequency. On the other hand, Gaussian data augmentation improves robustness against high frequencies while sacrificing robustness against low-frequency perturbations. For AutoAugment, we observe that its Fourier heatmap has the largest blue/yellow area around the center, indicating that AutoAugment is relatively robust to low-frequency to mid-frequency disturbances.

Image translation description: Model robustness under additive noise with fixed norm and different frequency distributions. For each channel of every CIFAR-10 test image, we sample independent identically distributed Gaussian noise, apply low/high-pass filters, and normalize the filtered noise to an L2 norm value of 8 before applying it to the image. We vary the bandwidth of the low/high-pass filter to generate two curves. The natural training model exhibits stronger robustness against low-frequency noise with a bandwidth of 3, while Gaussian data augmentation and adversarial training enhance the model’s robustness against high-frequency noise.

Image translation description: Relationship between the high-frequency energy fraction of CIFAR-10-C corruption and test accuracy. Each scatter point in the plot represents the evaluation results of a specific model on a specific type of corruption. The x-axis represents the score of high-frequency energy of the corruption type, and the y-axis represents the change in test accuracy compared to the natural training model. Overall, Gaussian data augmentation, adversarial training, and adding low-pass filters improve robustness against high-frequency corruption while reducing robustness against low-frequency corruption. The application of high-pass filters has a more significant accuracy drop for high-frequency corruption compared to low-frequency corruption. AutoAugment enhances robustness against almost all corruptions and achieves the best overall performance. The legend at the bottom shows the slope (K) and residual (r) of each fitted line.

Image translation description: (a) and (b): Fourier spectrum of adversarial perturbations. Given image X, initiating a PGD attack yields adversarial sample C(X), estimating the Fourier spectrum of adversarial perturbations that lead to misclassification of the image; (a) is the spectrum obtained from natural training; (b) is the spectrum obtained from adversarial training. The adversarial perturbations of the natural training model are uniformly distributed across frequency components. In contrast, adversarial training biases these perturbations towards lower frequencies. (C) and (D): Adding Fourier basis vectors with large norms to the image is a simple method for generating content-preserving black-box adversarial examples.

Conclusions:

1) Adversarial training pays attention to some high-frequency components rather than obsessing over low-frequency components.

2) AutoAugment helps improve robustness.

The open-source code mainly teaches how to draw similar schematic diagrams as in the paper.

Another paper from Eric Xing’s group has been previously published by a self-media on Zhihu:

High-frequency Component Helps Explain the Generalization of Convolutional Neural Networks

https://arxiv.org/pdf/1905.13545.pdf

Visualization of convolutions from natural training versus adversarial training

The paper experimented with several methods:

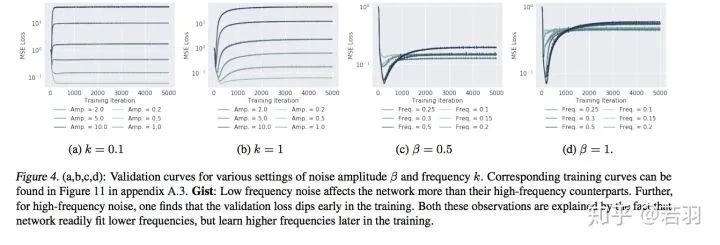
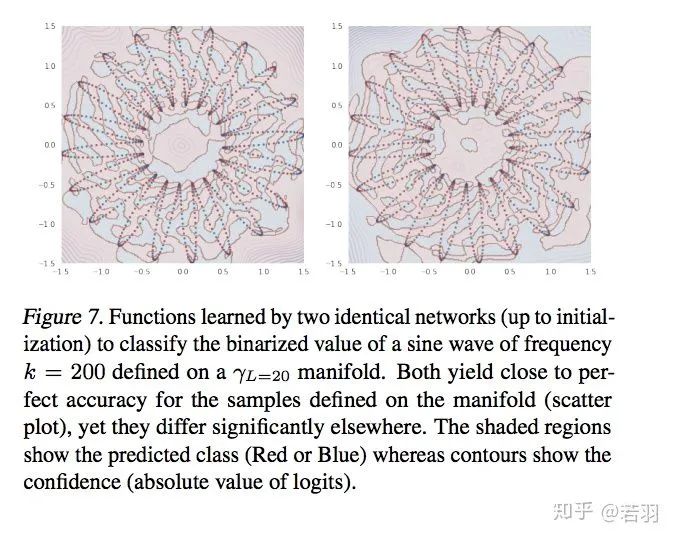
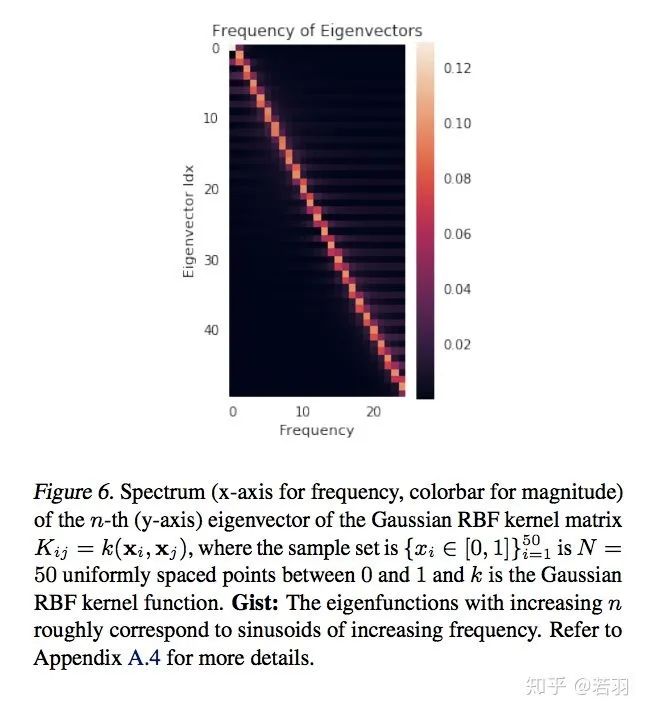
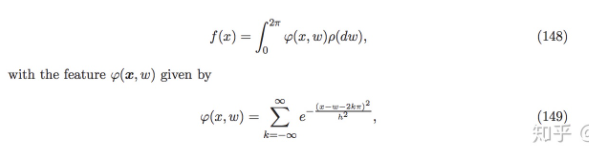
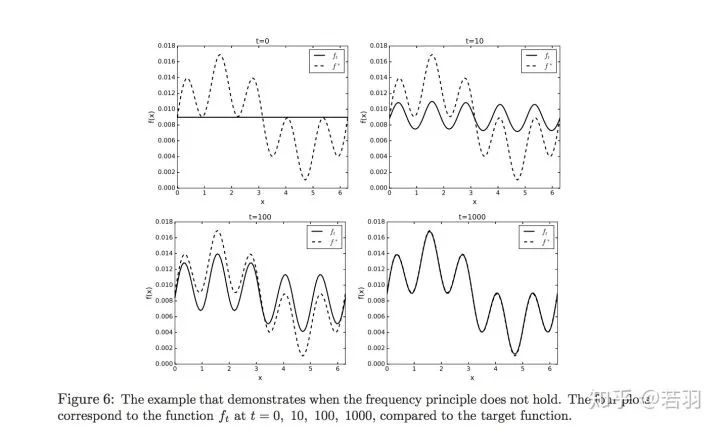
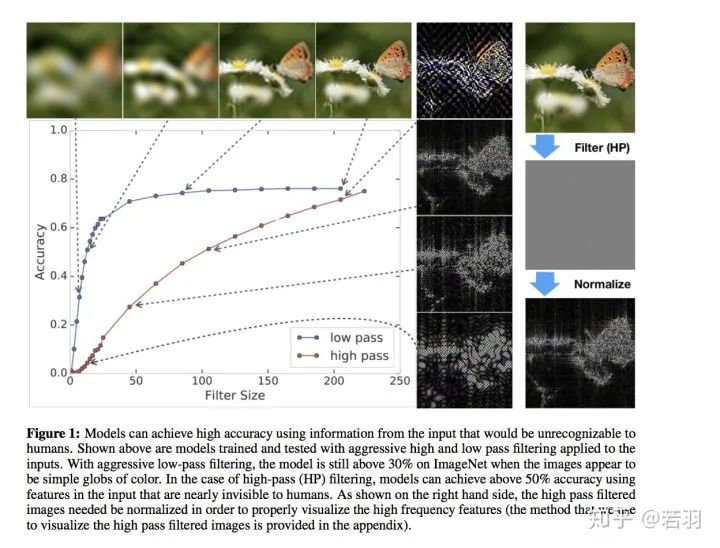
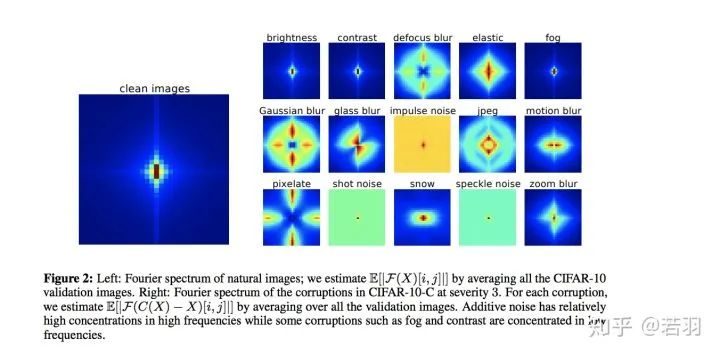
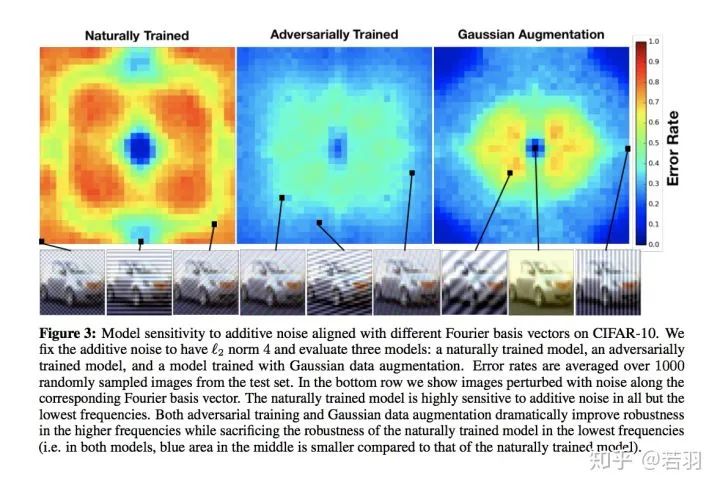
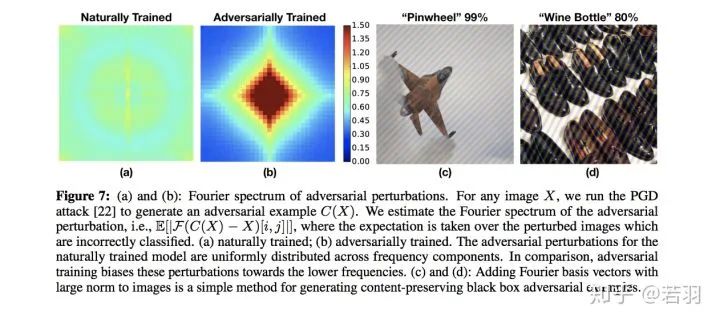
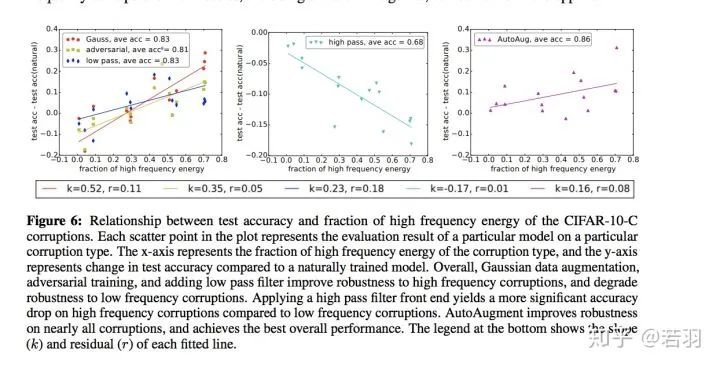
For a trained model, we adjusted its weights to make the convolution kernels smoother;
Directly filtering high-frequency information on the trained convolution kernels;
Adding regularization during the training of convolutional neural networks to make weights at adjacent positions closer.

Then concluded:

Focusing on low-frequency information helps improve generalization; high-frequency components may be related to adversarial attacks, but this cannot be too dogmatic.

The contribution is to provide detailed experimental evidence that Batch Normalization is useful for fitting high-frequency components and improving generalization.

Finally, it all comes down to just talking.

On this side, Professor Xu proves that the smoothness of ReLU aids in function optimization; on the other side, a recent work called Bandlimiting Neural Networks against Adversarial Attacks

https://arxiv.org/pdf/1905.12797.pdf

The ReLU function results in a piecewise linear function

Which can be decomposed into numerous frequency components.

For a hidden layer with N=1000 nodes and an input dimension of n=200, the maximum number of regions is approximately 10^200. In other words, even a moderately sized neural network can partition the input space into a vast number of sub-regions, easily exceeding the total number of atoms in the universe. When we train a neural network, we cannot expect at least one sample to exist within each region. For those regions without any training samples, the results of the linear function can be arbitrary because they do not contribute to the training objective function at all. Of course, most of these regions are very small. When we measure the expected loss function over the entire space, their contribution can be negligible because the chance of random sampling points falling into these tiny regions is very small. However, adversarial attacks pose new challenges, as adversarial samples are not naturally sampled. Given the enormous number of regions, these tiny regions are almost everywhere in the input space. For any data point in the input space, we can almost certainly find such a tiny region where the linear function is arbitrary. If a point within this tiny region is chosen, the output of the neural network may be unexpected. These tiny regions are the fundamental reason why neural networks are vulnerable to adversarial attacks.

Then, a method for adversarial defense is proposed, which is not well understood; readers are welcome to read the paper and provide insights in the comments section.

Although there is procrastination, I will share other related and interesting papers I come across in this area.

Source:

https://www.zhihu.com/question/59532432/answer/1510340606

Answer Two

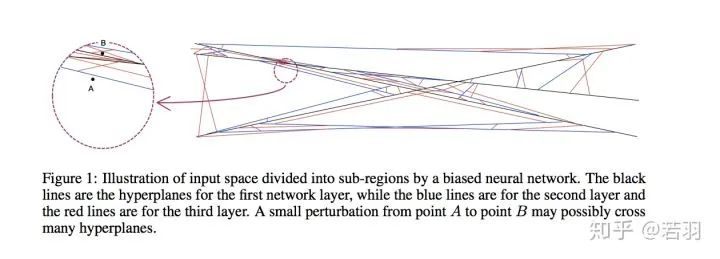
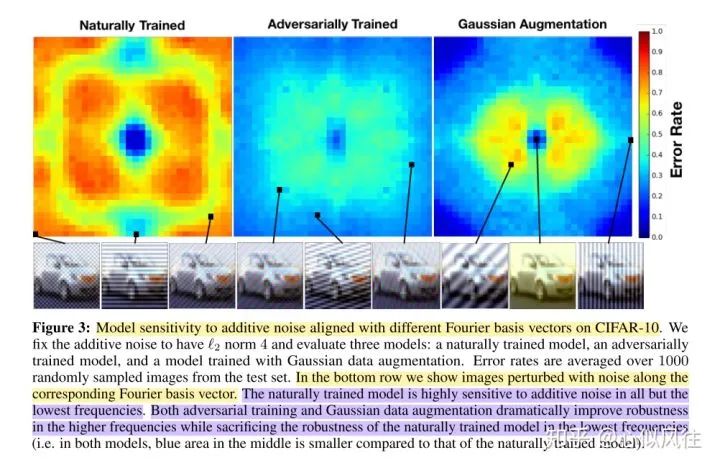
Author丨Xinsi Fengwang

After receiving the invitation, I paid attention to this issue for a while, thinking that I could save time by waiting for someone destined to answer this question, secretly delighted. However, after a long time, there wasn’t a serious and detailed answer. I could only come out and throw out a brick to attract jade.

It’s quite miraculous that I happened to read an article about understanding and analyzing model robustness from the frequency domain; some parts of this article also analyze this issue, and coincidentally, the experiments also used ResNet. Isn’t that a coincidence!

First, let me post the name of the paper:

A Fourier Perspective on Model Robustness in Computer Vision [1]

Firstly, deep learning models have achieved unprecedented success, but there is a significant problem: their robustness is poor, meaning that adding slight corruption to certain test images can lead to misclassification. One method to enhance robustness is to perform data augmentation on the training set images, allowing the trained model to resist corruption. However, the authors discovered that the same data augmentation methods, such as Gaussian augmentation and adversarial training, do not improve robustness for all corruption cases. Thus, the authors pose the question: Why do the same augmentation methods enhance performance for some corruptions while reducing it for others?

Then, the authors propose a hypothesis: Could it be that different corruptions provide different frequency information?

For CIFAR-10, the authors used Wide ResNet-28-10;

For ImageNet, the authors used ResNet-50.

Firstly

The authors analyzed the impact of different frequency information in images on the prediction accuracy of naturally trained models.

As shown in the above figure, the authors conducted experiments using the ResNet-50 model trained on ImageNet.

For low-frequency information, the authors directly applied low-pass filters to the test images’ frequency domain, allowing different amounts of low-frequency signals to pass through, with four typical filtered images displayed above the graph.

For high-frequency information, the authors applied high-pass filters in the frequency domain of the images and performed normalization. Different filter sizes allowed different amounts of high-frequency signals to pass through, with four typical filtered images displayed on the right side of the graph.

The x-axis of the graph represents the size of the filter, and the y-axis represents the classification accuracy.

The above graph illustrates that even with a very small low-pass filter size, the image looks like color blocks, and the human eye cannot distinguish what it is, the model still achieves over 30% accuracy (the first image obtained from the low-pass filter). For the high-pass filtered portion (the second image from the top), even though the human eye cannot distinguish what is in this image, the model still achieves 50% accuracy. Furthermore, when low-frequency information is scarce, increasing low-frequency information can quickly improve accuracy, but once a certain amount is reached, it no longer affects accuracy; the influence of high-frequency information on accuracy increases gradually, and is not as fast as that of low-frequency.

Secondly

For the CIFAR-10 training set, the authors analyzed the sensitivity of the Wide ResNet-28-10 model to additive noise.

The middle of the image represents the low-frequency signal area, with higher frequencies towards the edges.

For the CIFAR-10 training set, the trained model is Wide ResNet-28-10.

The naturally trained model is sensitive to all frequencies except for low-frequency corruption noise, while adversarial training and Gaussian augmentation enhance the model’s robustness against high-frequency corruption (lower error rates).

Again

For the ImageNet training set, the authors analyzed the sensitivity of the ResNet-50 model to additive noise.

The naturally trained model is sensitive to all frequencies except for low-frequency corruption noise. Gaussian augmentation sacrifices robustness against low-frequency perturbations while improving robustness against high-frequency ones. For AutoAugment, robustness against low, mid, and high frequencies gradually decreases.

Finally

The impact of increasing bandwidth on test accuracy from high-frequency and low-frequency signals.

For the CIFAR-10 training set, the model is Wide ResNet-28-10.

Compared to the naturally trained model, as the bandwidth of the noise filter increases, test accuracy decreases, and we find that the accuracy of models from Gaussian augmentation and adversarial training is higher than that of models from natural training.

Supplement 1: According to @Lost’s answer under this question, it is also recommended for everyone to read the paper he mentioned: Frequency Principle: Fourier Analysis Sheds Light on Deep Neural Networks [2]

https://arxiv.org/pdf/1901.06523.pdf

Supplement 2: It is also recommended for everyone to read the following paper: High-frequency Component Helps Explain the Generalization of Convolutional Neural Network [3]

https://openaccess.thecvf.com/content_CVPR_2020/papers/Wang_High-Frequency_Component_Helps_Explain_the_Generalization_of_Convolutional_Neural_Networks_CVPR_2020_paper.pdf

References

[1] A Fourier Perspective on Model Robustness in Computer Vision

[2] Frequency Principle: Fourier Analysis Sheds Light on Deep Neural Networks

[3] High-frequency Component Helps Explain the Generalization of Convolutional Neural Network

Good News!

Beginner’s Guide to Visual Knowledge Circle

Is now open to the public👇👇👇







Download 1: Chinese Version Tutorial for OpenCV-Contrib Extension Modules

Reply "Chinese Tutorial for Extension Modules" in the backend of the "Beginner's Guide to Vision" public account to download the first Chinese version of the OpenCV extension module tutorial available online, covering over twenty chapters on extension module installation, SFM algorithms, stereo vision, object tracking, biological vision, super-resolution processing, and more.

Download 2: 52 Lectures on Practical Python Vision Projects

Reply "Python Practical Vision Projects" in the backend of the "Beginner's Guide to Vision" public account to download 31 practical vision projects, including image segmentation, mask detection, lane line detection, vehicle counting, eyeliner addition, license plate recognition, character recognition, emotion detection, text content extraction, face recognition, etc., to help you quickly learn computer vision.

Download 3: 20 Lectures on Practical OpenCV Projects

Reply "20 Practical OpenCV Projects" in the backend of the "Beginner's Guide to Vision" public account to download 20 practical projects based on OpenCV, achieving advanced learning of OpenCV.

Group Chat

Welcome to join the public account reader group to communicate with peers. Currently, there are WeChat groups for SLAM, 3D vision, sensors, autonomous driving, computational photography, detection, segmentation, recognition, medical imaging, GAN, algorithm competitions, etc. (will gradually be subdivided in the future). Please scan the WeChat number below to join the group, and note: "Nickname + School/Company + Research Direction", for example: "Zhang San + Shanghai Jiao Tong University + Vision SLAM". Please follow the format for notes; otherwise, your request will not be approved. After successfully adding, you will be invited to the relevant WeChat group based on your research direction. Please do not send advertisements in the group; otherwise, you will be removed from the group. Thank you for your understanding~

Leave a Comment Cancel reply