Top Ten Classic Data Mining Algorithms: K-means

K-means and kNN may both start with ‘k’, but they are two different types of algorithms—kNN is a classification algorithm in supervised learning, while k-means is a clustering algorithm in unsupervised learning. The similarity between the two is that both utilize neighbor information to label categories.

Clustering is a very important learning paradigm in data mining, which refers to grouping similar unlabeled sample data into the same category, as the saying goes, “birds of a feather flock together.” K-means is the simplest and most efficient clustering algorithm, with the core idea being: the user specifies k initial centroids as the categories of clustering, and it iterates repeatedly until the algorithm converges.

In the k-means algorithm, centroids are used to represent clusters; it is easy to prove that the convergence of the k-means algorithm is equivalent to all centroids no longer changing. The basic k-means algorithm process is as follows:

Select k initial centroids (as initial clusters); repeat:
    For each sample point, calculate the nearest centroid and label it as the cluster corresponding to that centroid;
    Recalculate the centroids corresponding to k clusters; until centroids no longer change

For sample data in Euclidean space, the sum of squared errors (SSE) is used as the clustering objective function, and it can also be an indicator to measure the quality of different clustering results:

SSE=∑i=1k∑x∈Cidist(x,ci)SSE=∑i=1k∑x∈Cidist(x,ci)

This represents the sum of squared distances from the sample point xx to the centroid cici of cluster CiCi; the optimal clustering result should minimize SSE.

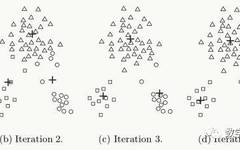
The following diagram shows an example of clustering three clusters through four iterations:

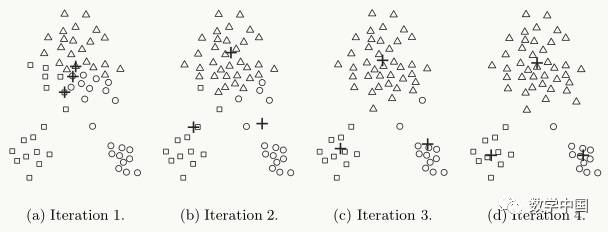
K-means has its drawbacks:

• K-means is locally optimal and can be easily affected by the initial centroids; for example, in the diagram below, inappropriate selection of initial centroids leads to suboptimal clustering results (larger SSE):

• 

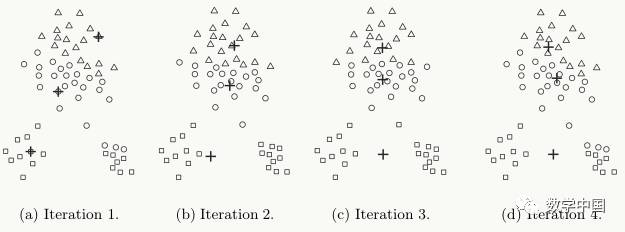
• Additionally, the selection of k directly affects the clustering results; the optimal k value should align with the structural information of the sample data itself, which is difficult to grasp, making the selection of the optimal k very challenging.

To address the aforementioned drawbacks, bisecting k-means has been developed based on the basic k-means algorithm. Its main idea is that a large cluster can split into two smaller clusters; to obtain k clusters, k-1 splits can be performed. The algorithm process is as follows:

Initially, there is only one cluster containing all sample points; repeat:
    Select one cluster to split from the clusters to be split, ensuring that the selected cluster minimizes SSE; until there are k clusters

In the above algorithm process, to find the local optimal solution from the clusters to be split, a brute-force method can be adopted: sequentially perform binary splits on each cluster to be split to find the optimal split. The clustering process of the bisecting k-means algorithm is shown in the figure:

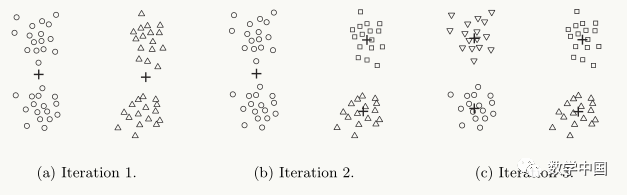
From the figure, we observe that the bisecting k-means algorithm is not very sensitive to the selection of initial centroids, as it initially selects only one centroid.

[1] Pang-Ning Tan, Michael Steinbach, Vipin Kumar, Introduction to Data Mining.[2] Xindong Wu, Vipin Kumar, The Top Ten Algorithms in Data Mining.

Author: Treant

Source: http://www.cnblogs.com/en-heng/