Time Series + Transformer: Understanding iTransformer

This article is about 3500 words long and is recommended to be read in 10 minutes.
This article will help you understand iTransformer and better utilize the attention mechanism for multivariate correlation.

1 Introduction

Transformers perform excellently in natural language processing and computer vision, but they do not perform as well as linear models in time series forecasting.

When embedding multiple variables into indistinguishable channels and applying attention, the performance and efficiency are inferior to simple linear layers. Transformers struggle to capture multivariate correlations (Figure 1), while linear models can better simulate multivariate correlations for accurate predictions. Researchers proposed iTransformer, which independently embeds the entire time series of each variable into a token to expand the local receptive field and better utilize the attention mechanism for multivariate correlation.

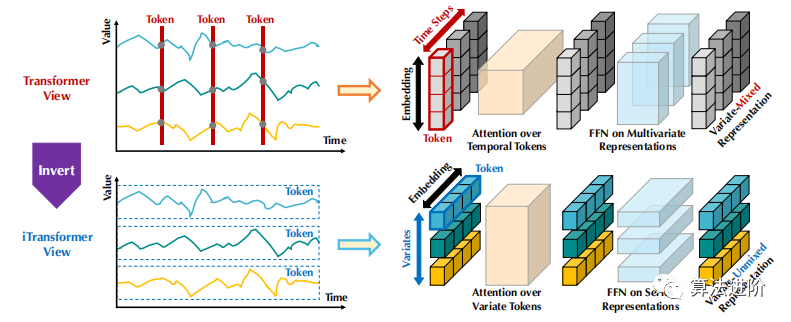
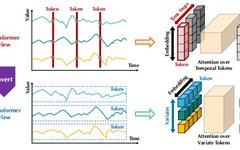
Figure 1 Comparison between the standard Transformer (top) and the proposed iTransformer (bottom). The Transformer embeds time markers that contain multivariate representations for each time step. The iTransformer independently embeds each sequence into variable tokens, allowing the attention module to describe multivariate correlations, while the feedforward network encodes the sequence representations.

iTransformer is the foundation for time series forecasting proposed after re-examining the Transformer structure, employing attention mechanisms for multivariate correlation analysis and using feedforward networks for sequence representation.Experiments show that iTransformer achieves state-of-the-art performance on real-world forecasting benchmarks, addressing the challenges faced by Transformer-based predictors.

Variants of Transformers have been proposed for time series forecasting, surpassing concurrent TCN and RNN-based predictions.

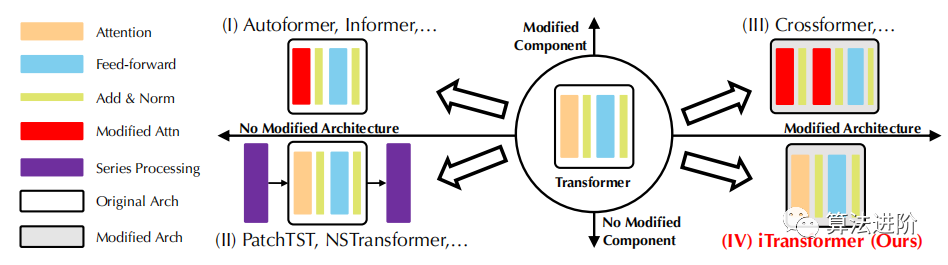
Existing variants can be categorized into four types: whether to modify components and architecture, as shown in Figure 2.

The first category mainly involves component adjustments, such as optimizing the attention module and the complexity of long sequences.

The second category fully utilizes Transformers, focusing on the intrinsic processing of time series.

The third category innovates Transformers in both components and architecture to capture dependencies across time and variables.

Unlike previous work, iTransformer does not modify any native components of the Transformer; instead, it adopts components in the reverse dimension and changes its architecture.

Figure 2 Classification of Transformer-based predictors by component and architecture modifications.

2 iTransformer

Multivariate time series forecasting involves historical observations X and predicting future values Y. Given T time steps and N variables, predicting future S time steps. There may be systematic time lags among variables in the dataset, and variables may differ in physical measurement and statistical distribution.

2.1 Structure Overview

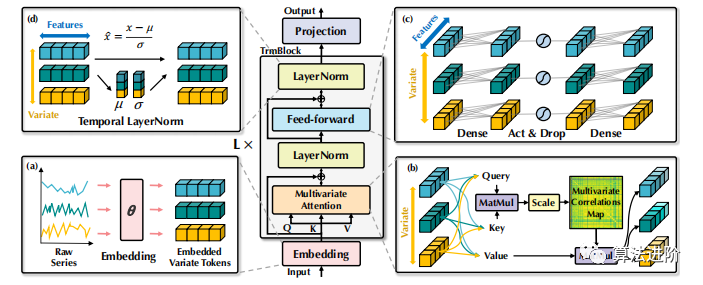
The proposed iTransformer adopts the encoder architecture of the Transformer, including embedding, projection, and Transformer blocks, as shown in Figure 3.

Figure 3 Overall structure of iTransformer, which has the same modular structure as the encoder of the Transformer. (a) The original sequences of different variables are independently embedded as tokens. (b) Self-attention is applied to the embedded variable tokens, enhancing interpretability and revealing multivariate correlations. (c) Sequence representations of each token are extracted through a shared feedforward network. (d) Layer normalization is used to reduce discrepancies between variables.

Embedding the entire sequence as a token.In iTransformer, based on the look-back sequence X:, n, the process of predicting the future sequence of each specific variable ˆY: n is simply represented as follows:

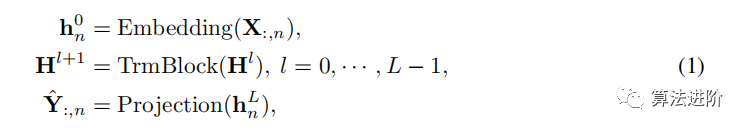
Where H={h1, · · · , hN }∈RN×D contains N embeddings of dimension D, where the superscript indicates layer index. The embedding: RT7→ RD and projection: RD7→ RS are both implemented by multi-layer perceptrons (MLP). Variable representations interact through self-attention and are independently processed by a shared feedforward network in each TrmBlock, eliminating the need for positional embeddings.

iTransformers.The architecture flexibly utilizes attention mechanisms, allowing for multivariate correlation and reducing complexity. A series of efficient attention mechanisms can be plugged in, with the number of tokens varying between training and inference, and the model can be trained on any number of variables. The reverse Transformer, named iTransformers, has advantages in time series forecasting.

2.2 Inverted Transformer Module Analysis

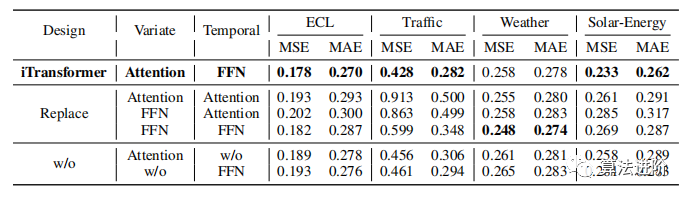
We organized a stack of L blocks composed of layer normalization, feedforward networks, and self-attention modules.

Layer Normalization

Layer normalization was initially used to improve the convergence and stability of deep networks. In the Transformer predictor, it normalizes multivariate representations at the same timestamp. In the reverse version, normalization is applied to the sequence representation of individual variables (as in formula 2), effectively addressing non-stationary issues. All sequence tokens are normalized to a Gaussian distribution, reducing discrepancies caused by inconsistent measurements. In previous architectures, different tokens at time steps would be normalized, leading to excessive smoothing of the time series.

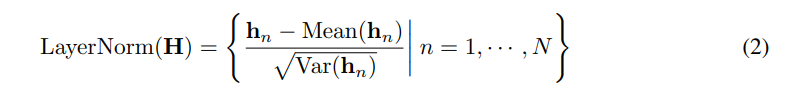
Feed-Forward Network

The Transformer uses a feed-forward network (FFN) as the fundamental building block for encoding token representations, applying the same feed-forward network to each token. In the reverse version, the FFN is used for the sequence representation of each variable token, and by stacking reverse blocks, they are dedicated to encoding the observed time series and decoding the representations of future sequences using dense nonlinear connections. Stacking reverse blocks can extract complex representations to describe time series and use dense nonlinear connections to decode representations of future sequences. Experiments show that this division of labor helps to leverage the benefits of linear layers in terms of performance and generalization capability.

Self-Attention

The reverse model treats time series as independent processes, comprehensively extracting time series representations through self-attention modules, employing linear projections to obtain queries, keys, and values, calculating pre-Softmax scores, revealing correlations between variables and providing a more natural and interpretable mechanism for multivariate sequence forecasting.

3 Experiments

We comprehensively evaluate the performance of iTransformer in time series forecasting applications, validate its versatility, and explore the effectiveness of Transformer components in the reverse dimension of time series.

In the experiments, we used 7 real datasets, including ECL, ETT, Exchange, Traffic, Weather, Solar, and PEMS, as well as Market datasets. We consistently outperformed other baselines. Appendix A.1 provides a detailed description of the datasets.

3.1 Prediction Results

This article conducted extensive experiments to evaluate the predictive performance of the proposed model against advanced deep predictors. Ten well-known predictive models were chosen as baselines, including Transformer-based, linear, and TCN methods.

Table 1 Multivariate prediction results for PEMS with prediction lengths S ∈ {12, 24, 36, 48} and other predictions with S ∈ {96, 192, 336, 720}, fixing the look-back length T = 96. Results are averaged across all prediction lengths. Avg indicates further averaging by subsets. Complete results are listed in Appendix F.4.

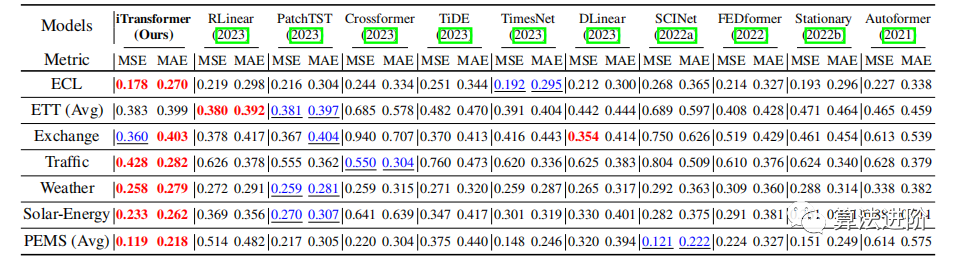
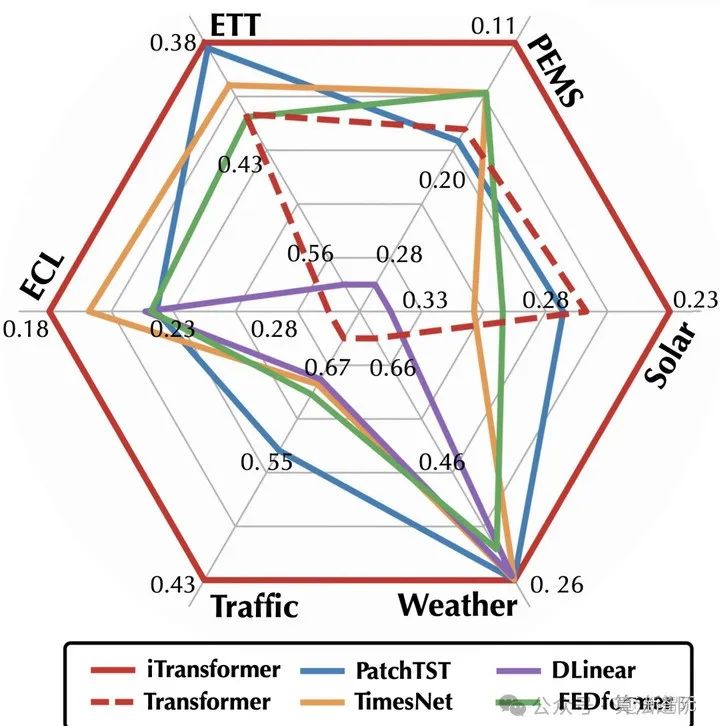
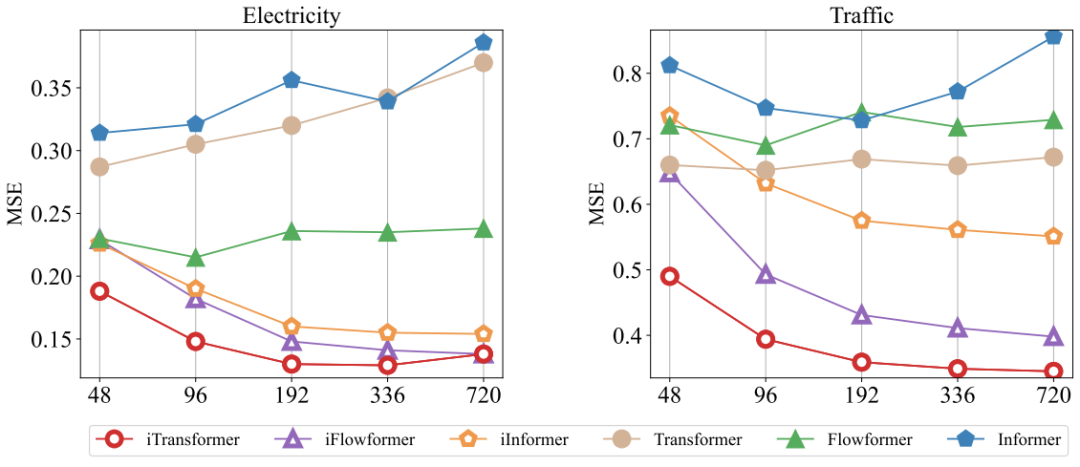
The results show that the iTransformer model performs best in predicting high-dimensional time series, outperforming other predictors. PatchTST fails in some cases, possibly due to its patching mechanism not handling rapid fluctuations. In contrast, iTransformer aggregates the entire sequence changes into sequence representations, making it better suited for such situations. The performance of Crossformer remains below that of iTransformer, indicating that interactions from inconsistent patches across different multivariate time may introduce unnecessary noise into predictions. Thus, the native components of the Transformer can handle time modeling and multivariate correlation, while the proposed reverse architecture can effectively address real-world time series forecasting scenarios.

3.2 Generalizability of the iTransformer Framework

This section applies the framework to evaluate Transformer variants such as Reformer, Informer, Flowformer, and FlashAttention to enhance predictor performance, improve efficiency, and generalize unknown variables while better utilizing historical observations.

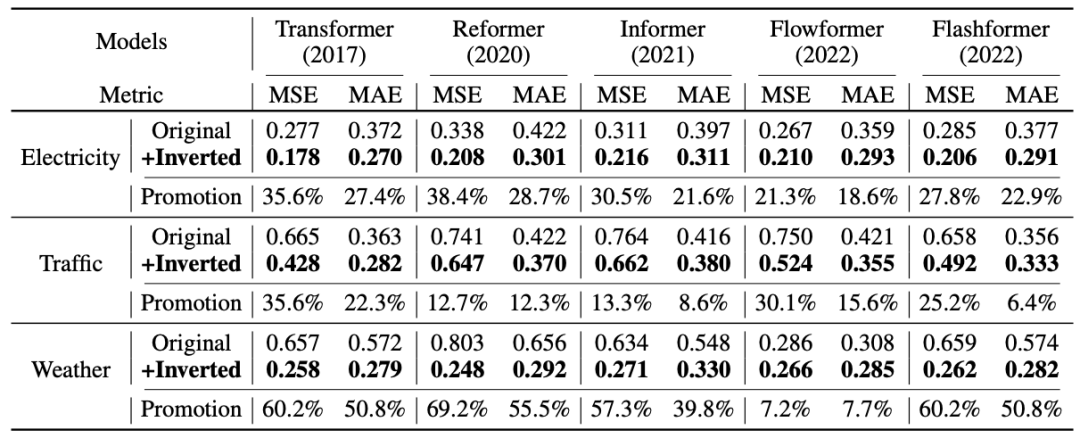
Predictive performance can be enhanced!

The framework achieved an average improvement of 38.9% on the Transformer, 36.1% on the Reformer, 28.5% on the Informer, 16.8% on the Flowformer, and 32.2% on the Flashformer. By introducing efficient linear complexity attention, iTransformer addresses computational issues caused by a large number of variables. Therefore, the ideas of iTransformer can be widely practiced on Transformer-based predictors.

Table 2 Performance improvements achieved by our inverted framework. Flashformer refers to the Transformer equipped with hardware-accelerated FlashAttention. We report average performance and relative MSE reduction (improvement). Complete results can be found in Appendix F.2.

Can generalize unknown variables!

The iTransformer model has generalization capabilities over unseen variables by inverting the conventional transformer. The number of input tokens is flexible, and the number of variable channels is not limited. The feedforward network is applied independently to variable tokens, learning shared and transferable patterns in time series. Compared to the channel independence strategy, iTransformer directly predicts all variables, which generally performs better, indicating that the FFN can learn transferable time series representations, as shown in Figure 4. This provides potential directions for building foundational models based on iTransformer.

Figure 4 Generalization performance on unseen variables. We divided the variables of each dataset into five folders, trained the model with 20% of the variables, and used the partially trained model to predict all variables. iTransformers can be efficiently trained and exhibit good generalization capabilities.

Can utilize longer historical observations!

Predictive performance does not necessarily improve with increasing look-back length in Transformers, possibly due to attention dispersion. However, linear prediction is theoretically supported by statistical methods and utilizes expanded historical information. We evaluate the performance of Transformers and iTransformer under increasing look-back lengths in Figure 5, finding that utilizing MLP in the time dimension is more reasonable, allowing Transformers to benefit from the expanded look-back window for more accurate predictions.

Figure 5 Predictive performance under look-back lengths T ∈ {48, 96, 192, 336, 720} and fixed prediction length S = 96. While the performance of Transformer-based predictors does not necessarily benefit from increased look-back lengths, the reverse framework allows standard Transformers and their variants to perform better on expanded look-back windows.

3.3 Model Analysis

Ablation Study.To validate the rationale of Transformer components, ablation experiments were conducted, including component replacement (Replace) and removal (w/o) experiments. The results shown in Table 3 indicate that iTransformer performs the best, while the standard Transformer performs the worst, revealing potential risks of traditional architectures.

Table 3 Ablation on iTransformer. In addition to removing components, we also replaced different components across dimensions to learn multivariate correlations (variables) and sequence representations (time). Average results across all prediction lengths are listed here.

Analysis of Sequence Representations.To validate that the feedforward network is beneficial for extracting sequence representations, we performed representation analysis based on CKA similarity. The results show that iTransformers learn more suitable sequence representations by inverting dimensions, achieving more accurate predictions, as shown in Figure 6. This indicates that the inverted Transformer is worth fundamentally transforming the prediction backbone.

Figure 6 Analysis of sequence representations and multivariate correlations. Left: Comparison of mean squared error (MSE) and CKA similarity between the representations of the Transformer and iTransformer. Higher CKA similarity indicates representations more conducive to accurate predictions. Right: Visualization of multivariate correlations of original time series and scores mapped from inverted self-attention learning.

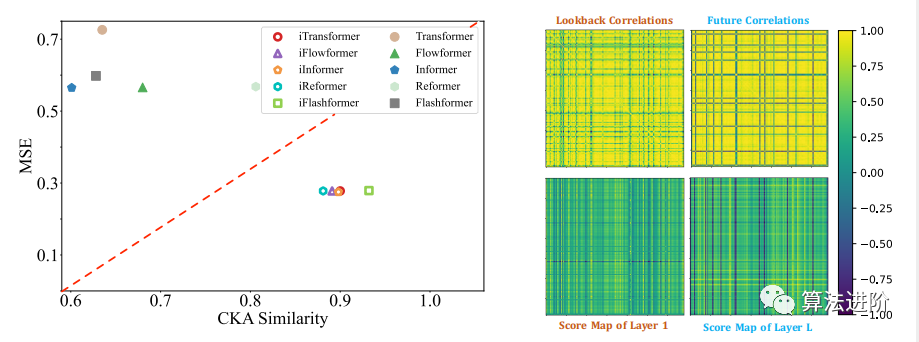
Multivariate correlation analysis. By assigning multivariate correlation responsibilities to the attention mechanism, the learned mappings have enhanced interpretability. For instance, in the solar energy case shown in Figure 6, the shallow attention layers show similarities in correlation with the original input sequence, while deeper layers correlate with future sequences, validating that reverse operations can provide interpretable attention.

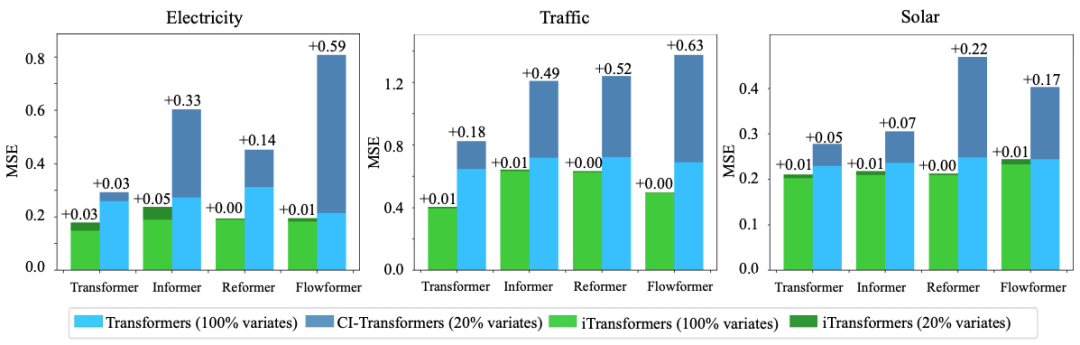
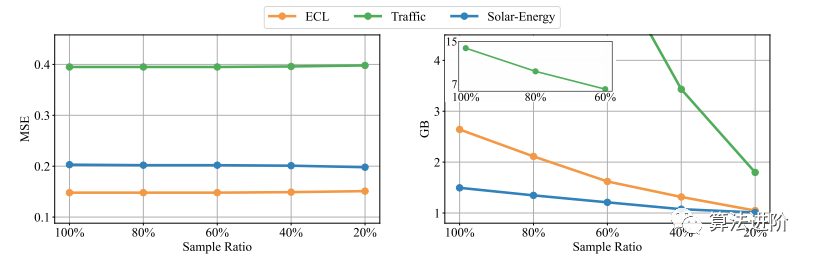
Efficient training strategy. This article proposes a new training strategy that utilizes the previously proven variable generation capability to train high-dimensional multivariate sequences. Specifically, a subset of variables is randomly selected in each batch, using only the selected variables to train the model. Due to our inversion, the number of variable channels is flexible, allowing the model to predict all variables for forecasting. As shown in Figure 7, the performance of our proposed strategy remains comparable to full variable training while significantly reducing memory usage.

Figure 7 Analysis of the efficient training strategy. While performance (left) remains stable across different sampling ratios of partially trained variables in each batch, memory usage (right) can be significantly reduced. A comprehensive model efficiency analysis can be found in Appendix D.

References: “ITRANSFORMER: INVERTED TRANSFORMERS ARE EFFECTIVE FOR TIME SERIES FORECASTING”

Code: http://github.com/thuml/iTransformer

Editor: Huang Jiyan